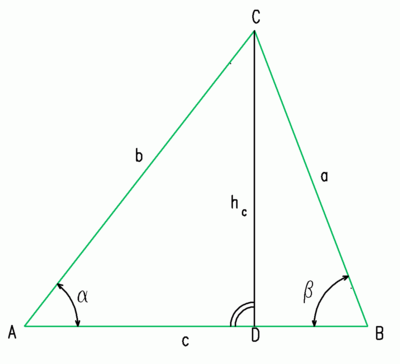
In jedem Dreieck gilt:
Beweis:
(1a)
(2a)
und
(1b)
(2b)
(2a) und (2b) gleich gesetzt
(3)
oder
(4a)
analog gilt damit der Sinussatz für alle drei Seiten und Winkel
(4b)
oder auch
(5)
1. Ergänzung:
Diese Ergänzung gehört zwar nicht direkt zum Sinussatz, aber:
wobei der Radius des Umkreises des Dreiecks ist.
1. Beweis:
(2.1)
weil der Mittelpunktswinkel doppelt so groß ist wie der Umfangswinkel ist (hier ) ist auch
(2.2)
oder
(2.3)
also ist analog auch
(2.4)
2. Beweis
Weil alle Umfangswinkel über einer Sehne (hier ) gleich groß sind ist
(3.1)
Nach dem Satz des Thales ist der Umgangswinkel über einer Sehne die der Durchmesser ist (hier ) ein rechter Winkel.
(3.2)
(3.3)
(3.4)
umgewandelt
(3.5)
also ist analog auch
(3.6)
2. Ergänzung:
Diese Ergänzung gehört zwar auch nicht direkt zum Sinussatz, aber mit als Dreiecksfläche ist:
Daraus mit (3.6)
Beweis:
Die Dreiecksfläche ist nach der ersten Skizze
(4.1)
weiter ist
(4.2)
nach (3.6) ist
(4.3)
(4.4)
in (4.2) eingesetzt
(4.5)
in (4.1) eingesetzt
(4.6)
oder
(4.7)
umgewandelt
(4.8)
und damit
(4.9)