MathemaTriX ⋅ Theorie. Klasse 7

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

Klassen Klasse 5 Klasse 6 Klasse 7 Klasse 8 Klasse 9 Klasse 10 Klasse 11 Klasse 12

Vorgabe des Ministeriums

Grundrechnungen

Definitionen der Grundrechenarten

Die vier Grundrechenarten

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses
Addition	plus	+	$2$        $+$      $7$      $=$	$9$
(addieren, erhöhen)			Summand $+$ Summand $=$	Summe
Subtraktion	minus	−	$65$      $-$      $22$      $=$	$43$
(subtrahieren, reduzieren, vermindern, abziehen)			Minuend $-$ Subtrahend $=$	Differenz
Multiplikation	mal	⋅  (×)	$9$      $\cdot$      $13$      $=$	$117$
(multiplizieren, vervielfachen, -fach)			Faktor  ⋅  Faktor $=$	Produkt
Division	durch	:  (÷, /)	$84$      $:$      $7$      $=$	$12$
(dividieren, teilen)			Dividend $:$ Divisor $=$	Quotient

Das Symbol = ist ein Gleichheitszeichen. Es steht für die Gleichheit zweier Ausdrücke. Es wird in einem eigenen Abschnitt genauer erklärt.

Das Symbol × für die Multiplikation wird kaum benutzt, weil es leicht mit dem Symbol oder dem Buchstaben x für die Variable x verwechselt werden kann. Wozu in Rechnungen Buchstaben verwendet werden, werden wir später lernen. Für die Multiplikation wird in diesem Buch das Symbol · benutzt.
Das ist ein Punkt ungefähr auf halber Höhe einer Ziffer notiert.

Für die Division benutzt man auch Punkte : Die anderen Symbole für die Division / und ÷ werden seltener benutzt.
Typisch wird allerdings / bei den Einheiten verwendet, beispielsweise in der Geschwindigkeit (km/h). In diesem Beispiel sagt man "Kilometer pro Stunde". Mit dem Wort "pro" ist Division gemeint.

Weil für Multiplikation und Division Punkte als Symbole verwendet werden, nennt man die beiden Rechenarten zusammen Punktrechnungen.

Die Symbole für die Addition + und die Subtraktion – verwenden dagegen beide Striche. Daher nennt man diese beiden Rechenarten zusammen Strichrechnungen.

Bei Addition und Multiplikation spielt jeweils die Reihenfolge keine Rolle:

$5+6+11=6+11+5=\ 11+6+5\ =\ 22$

Die Reihenfolge spielt keine Rolle bei der Addition.

$2\cdot 5\cdot 3=5\cdot 3\cdot 2=\ 2\cdot 3\cdot 5\ =\ 30$

Die Reihenfolge spielt keine Rolle bei der Multiplikation.

Bei Subtraktion und Division ist die Reihenfolge wichtig. Das Ergebnis ist nicht das Gleiche, wenn die Reihenfolge anders ist:

$5-3+2=4\$ aber $\ 5-2+3\ =\ 6$

$10\cdot 5:2=25\$ aber $\ 10\cdot 2:5\ =\ 4$

Weitere Ausdrücke für die vier Grundrechenarten

Im Alltag gibt es allerdings einige Worte, die irgendeine Rechenart bedeuten können:

Schneiden, Kürzen (zum Beispiel Gehalt) und so weiter könnte minus bedeuten

Wachsen, zwei Sachen zusammen, insgesamt könnte plus bedeuten

in einige gleiche Teilen schneiden könnte doch geteilt durch bedeuten

... und so weiter ...

Das Gleichheitszeichen

Ein Symbol, das bisher nicht erklärt wurde, ist das Gleichheitszeichen "=". Es wird benutzt, um zu zeigen, dass der Ausdruck links des Zeichens das Gleiche ist, wie der Ausdruck rechts des Zeichens. Dies betrifft sowohl den Wert als auch die Einheit.

$20=4\cdot 5\ \$ ✔(richtig)

$20\ {\text{Kartoffeln}}=4\cdot 5\ {\text{Kartoffeln}}\ \$ ✔(richtig)

$20\ {\text{Kartoffeln}}=4\cdot 7\ {\text{Kartoffeln}}\ \$ ✘(falsch: falscher Wert)

$20\ {\text{Birnen}}=4\cdot 5\ {\text{Kartoffeln}}\ \$ ✘(falsch: falsche Einheit)

$10m\cdot 5=50$ ✘(falsch: rechts fehlt die Einheit m)

Wie man mit Einheiten arbeitet, werden wir genauer im entsprechenden Kapitel lernen. Da werden wir auch erfahren, dass

$15m=150dm$

doch richtig ist.

Es gibt allerdings Gleichungen zwischen mehr als zwei Ausdrucken ("Gleichungsketten"), wie wir vorher gesehen haben:

$5+6+11=6+11+5=\ 11+6+5\ =\ 22$

Bei Gleichungsketten sind alle Ausdrücke gleich, daher kann man in diesem Beispiel auch schreiben:

$6+11+5=\ 22\quad$ oder $\quad 5+6+11=\ 11+6+5$

Es gilt daher allgemein:

• wenn $\ a=b\$ dann auch $\ b=a\$

• wenn $\ a=b=c$ dann auch $\ a=c\$

Gleichungsketten kann man allerdings in der Regel nicht bei sogenannten Äquivalenzumformungen benutzen, wie wir später lernen werden.

Die Gleichung zwischen zwei Ausdrucke spielt allerdings eine wichtige Rolle beim Einsetzen, ein Verfahren, das wir im entsprechenden Kapitel lernen werden.

Negative Zahlen

Das Minuszeichen benutzt man nicht nur bei der Subtraktion, sondern auch um sogenannte negative Zahlen zu bezeichnen. Was die negativen Zahlen sind, kann man ziemlich einfach verstehen, wenn man sich vorstellt, in einem Aufzug zu sein. Betrachten wir die folgende Bilderfolge:

$\qquad \qquad \qquad$

$\qquad \qquad \qquad$

$\qquad \qquad \qquad$

$\qquad \qquad \qquad$

$\qquad \qquad \qquad$

Im ersten Bild fängt man vom Erdgeschoss an, dieses kann man mit der Zahl 0 bezeichnen. Dann fährt man mit dem Aufzug 2 Stockwerke nach oben. Die Richtung nach oben kann man mit Plus (+) bezeichnen. Das ist im Bild zu sehen. 0+2=2. Im dritten Bild fährt man aus dem 2. Stock 3 Stockwerke weiter nach oben (+ Richtung). 2+3=5. Im vierten Bild fährt man 8 Stockwerke nach unten. Nach unten kann man mit Minus (−) bezeichnen, da die Stockwerke weniger werden. Wenn man aber 5−8 rechnet, kann das Ergebnis nicht 3 sein. 3 ist oberhalb des Erdgeschosses, wir sind aber jetzt in dritten Untergeschoss. Um die Stockwerke unter dem Erdgeschoss zu bezeichnen, braucht man etwas Neues: das Minuszeichen vor dem Stockwerk! Wir sind also im Stock −3, also 3 Stockwerke unterhalb des Erdgeschosses.

Im fünften Bild fährt man ein Stockwerk weiter nach unten. Wir waren im Stock −3 und nach unten bedeutet minus. Am Ende sind wir 4 Stockwerke unter der Erde, also im Stock −4: −3−1=−4. Wenn also beide Zahlen negativ sind, addiert man ihren sogenannten Betrag (3 und 1) und schreibt vor dem Ergebnis wieder ein Minus. Im sechsten Bild fährt man aus dem 4 Stock unter der Erde (−4) 5 Stockwerke nach oben (nach oben bedeutet Plus machen) und befindet sich am Ende einen Stock oberhalb des Erdgeschosses (bei +1): −4+5=1. Wenn man zwei Zahlen mit unterschiedlichem Vorzeichen hat, subtrahiert man die Beträge (größerer Betrag minus kleineren Betrag, hier: 5−4=1) und schreibt man vor dem Ergebnis das Vorzeichen des größeren Betrags (also hier von 5, da sie mehr als 4 ist). Im vierten Bild haben wir 5−8 gerechnet. Da haben wir wieder die Beträge subtrahiert (größerer minus kleineren: 8−5=3) und im Ergebnis haben wir wieder das Vorzeichen des größeren Betrags geschrieben (also das Minus, das vor 8 steht): 5−8 = −3.

Zusammengefasst: Wenn man zwei Zahlen mit dem gleichen Vorzeichen hat (z.B. 4+7 oder −3−5), dann addiert man die Beträge (4+7=11 und 3+5=8) und schreibt vor dem Ergebnis das Vorzeichen: (4+7=11 und −3−5 = −8). Wenn die eine Zahl positiv (+) ist und die andere negativ(−), subtrahiert man die Beträge und schreibt vor dem Ergebnis das Vorzeichen des größten Betrags: $\qquad \qquad \qquad$ 4−7=−3 $\qquad \qquad \qquad$ 15−9=6

Negative Zahlen werden immer mit einem Minus davor geschrieben, z.B. −6 oder −7,453 oder $-{\sqrt {87}}$. Positive Zahlen werden mit einem Plus davor geschrieben, z.B. +6 oder +7,453 oder $+{\sqrt {87}}$. Bei positiven Zahlen kann man das Vorzeichen auslassen. Zum Beispiel ist 6 die positive Zahl +6, mit 7,453 wird die positive Zahl +7,453 gemeint und mit ${\sqrt {87}}$ einfach $+{\sqrt {87}}$.

Wenn allerdings das Plus oder das Minus nach der Zahl geschrieben wird, bedeutet es nicht, dass es eine positive oder negative Zahl ist. In diesem Fall erwartet man, dass noch eine Zahl folgen soll. 3− ist einfach unvollständig und auf gar keinen Fall die Zahl Minus drei ...

Weiteres über Rechnungen mit negativen Zahlen werden wir im Teilkapitel über die Plusminusregel lernen.

Das Komma bei Dezimalzahlen

Noch ein wichtiger Punkt bei der Schreibweise muss man noch kurz ansprechen. Und es geht hier genau um den Punkt.

Wenn man mit dem Taschenrechner die Division 2 durch 7 macht, kommt etwas wie folgendes vor:

$0.28571428...$

Das ist eine Zahl, die kleiner als eins ist. Auf Deutsch allerdings schreibt man:

$0{,}28571428...$

Falls der Unterschied nicht klar ist:

im ersten Fall steht zwischen 0 und dem Rest der Zahl ein Punkt:

$0\quad .\quad 28571428...$

im zweiten Fall ein Komma:

$0\quad {,}\quad 28571428...$

Man sagt auf Deutsch "Null Komma zwei acht fünf sieben...". Dieser Unterschied muss einem bewusst sein!

Auf Englisch und bei den meisten Taschenrechnern schreibt man

$8970063.4583$

oder sogar

$8{,}970{,}063.4583$.

Auf Deutsch und in ein paar anderen Sprachen werden die beiden Teile umgekehrt durch ein Komma getrennt:

$8970063{,}4583$

oder sogar

$8.970.063{,}4583$.

Auf diese Tatsache sollte man aufpassen!

Insbesondere wenn Menschen mit unterschiedlichen Kulturen, Sprachen oder Notationen Daten miteinander austauschen, kann dieser Unterschied für Verwirrung sorgen. Beim internationalen Datenaustausch und bei Programmiersprachen wird daher praktisch durchgehend der Punkt und nicht das Komma als Trennzeichen verwendet, in diesem Buch (wie allgemein auf Deutsch) allerdings das Komma.

Addition

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses
Addition	plus	+	2        +      7      =	9
(addieren, erhöhen)			Summand + Summand =	Summe

Beispiele: a) 35,7 + 59367 + 95382,89 + 567332,76=?       b) 56333,76 + 0,089 + 33727,727 + 9=?

Lösungen

Aufgabe a 2 2 1 2 1 2   1 0 0 0 0 0 3 5 , 1 0 5 9 3 6 7 , 0 0 0 9 5 3 8 2 , 8 9 5 6 7 3 3 2 , 7 6  7 2 2 1 1 8 , 3 5

Aufgabe b 1 1 0 2 1   1 1 5 6 3 3 3 , 7 6 0 0 0 0 0 0 , 0 8 9 3 3 7 2 7 , 7 2 7 0 0 0 0 9 , 0 0 0  9 0 0 7 0 , 5 7 6

Man schreibt die Zahlen, die man addieren will, untereinander. Die Kommas müssen untereinander sein! Wenn eine Zahl kein Komma hat, dann schreibt man ein Komma am Ende der Zahl.

Um die Aufgabe übersichtlicher zu machen, schreibt man links und rechts der Zahlen Nullen(0), wenn Ziffer (im Vergleich zu den anderen Zahlen) „fehlen“.

Man addiert die Zahlen von jeder Spalte und fängt mit der rechten Spalte an (und dann immer eine Spalte nach links). Die Summe der Ziffer der Spalte schreibt man unterhalb dieser Spalte.

Wenn die Summe der Ziffer in der Spalte mehr als 9 ist, dann schreibt man unterhalb der Spalte nur die letzte Ziffer und die restlichen oberhalb der nächsten Spalte links. Z.B. bei der Aufgabe a ist die Summe der Ziffer der Spalte rechts (mit der man anfängt) 0+0+9+6=15. Man schreibt darunter 5 (die letzte Ziffer) und 1 (15 ohne 5) oberhalb der nächsten Spalte links usw. Hier ist Aufgabe a Schritt zum Schritt gezeigt:

Aufgabe a Schritt zum Schritt gelöst
35,7 + 59367 + 95382,89 + 567332,76=?

Subtraktion

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses
Subtraktion	minus	−	65      −      22      =	43
(subtrahieren, reduzieren, vermindern, abziehen)			Minuend − Subtrahend =	Differenz

Beispiele: a) 9,2-6,7       b) 9,5-6,4       c) 4752,8–203,007

Man schreibt die Zahlen untereinander. Die Kommas müssen untereinander sein! Wenn eine Zahl kein Komma hat, dann schreibt man ein Komma am Ende der Zahl.

Die Zahl oben muss genau so viele Ziffer vor und nach dem Komma haben, wie die Zahl unten. Daher schreibt man rechts der Zahl oben Nullen(0), wenn Ziffer in den Nachkommastellen (im Vergleich zur Zahl unten) „fehlen“.

Man subtrahiert die Zahlen von jeder Spalte (oben minus unten) und fängt mit der rechten Spalte an (und dann immer eine Spalte nach links).

Wenn die Ziffer oben kleiner als die Ziffer unten ist, dann addiert man zu dieser Ziffer 10 und subtrahiert von der nächsten Ziffer oben links eins. In der nächsten Spalte links benutzt man dann oben die reduzierte Ziffer. Beispielsweise:

Aufgaben a und b: 9,2−6,7=?     9,5-6,4=?

Bei größeren Zahlen macht man den ganzen Vorgang bei jedem Schritt.

Aufgabe c: 4752,8–203,007=?

Noch ein paar gelöste Beispiele:

Bsp. A 453,803−452,944=0,857	Bsp. B 504,6−3,6003=500,997	Bsp. C 200−199,9998=0,0002

Multiplikation

Definition der Multiplikation

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses
Multiplikation	mal	⋅  (×)	9      ⋅      13      =	117
(multiplizieren, vervielfachen, -fach)			Faktor  ⋅  Faktor =	Produkt

Zunächst einmal erklären wir die Bedeutung der Multiplikation.

$5\cdot 3$ bedeutet, dass man $5$ mal die $3$ zueinander addiert (plus macht). Also $\textstyle \ 5\cdot 3=\underbrace {3+3+3+3+3} _{5\ mal}=15$. Allerdings spielt bei der Multiplikation die Reihenfolge keine Rolle. $\textstyle \ 5\cdot 3=3\cdot 5$. Letzteres ($\textstyle 3\cdot 5$) bedeutet drei mal die 5 zueinander addieren: $\textstyle \ 3\cdot 5=\underbrace {5+5+5} _{3\ mal}=15$.

Mit Hilfe der Addition kann man ein Multiplikationstabelle erstellen, sie wird das kleine Einmaleins genannt.

das kleine Einmaleins

Multiplikation mit Hilfe der Einmaleins-Tabelle

Mit Hilfe der Einmaleinstabelle (die man allerdings schon auswendig lernen könnte) kann man Multiplikationen zwischen Zahlen mit einer Ziffer ganz schnell berechnen:

2 mal 7 mit Hilfe der Einmaleinstabelle finden

Zeile "2" wählen

Spalte "7" wählen

Box wo sie sich treffen wählen

Ergebnis: 14

Und noch ein paar Beispiele:

Die Reihenfolge Spielt...	keine Rolle! 5x3=3x5
Ebenfalls: 7x8...	... = 8x7!
noch ein Beispiel

Multiplikation von Zahlen mit mehreren Ziffern und Nachkommastellen

a) $5\cdot 3$

b) $5\cdot 30$

c) $5\cdot 37$

d) $4\cdot 37$

e) $40\cdot 37$

f) $37\cdot 45$

g) $0{,}45\cdot 0{,}000037$

h) $450\cdot 37000$

Beispiel a haben wir im Abschnitt über Definition schon beantwortet: $5\cdot 3=3+3+3+3+3=15$

Bevor wir mit den restlichen Beispielen weitermachen, müssen wir zwei Sachen noch erklären.

1. Bemerkung: Multiplizieren mit Klammern
   Wenn etwas in Mathematik in Klammern steht, ist es so gemeint, dass die Rechnung in den Klammern erst gemacht werden muss. Wenn wir $3\cdot (2+5)$ berechnen wollen, rechnen wir erst $\ 2+5$ aus, also was in den Klammern steht. $2+5=7$. Dann führen wir die Multiplikation aus: $3\cdot 7=21$. Hätten wir erst $3\cdot 2$ gerechnet und dann $+5$, wäre das Ergebnis falsch: $3\cdot 2=6\ \ {\text{und}}\ \ 6+5=11$.
   Das bedeutet dann, dass man die Zahl außerhalb der Klammern erst mit jedem Summand in den Klammern multiplizieren muss und dann diese Produkte addieren. $3\cdot (2+5)$ ist nicht $3\cdot 2+5$. Man muss erst die Zahl außerhalb der Klammern (3) erst mit jedem Summand in den Klammern (2 und 5) multiplizieren $3\cdot 2=6\ \ {\text{und}}\ \ 3\cdot 5=15$ und dann diese Produkte (6 und 15) addieren: $6+15=21$ (also das richtige Ergebnis). Man schreibt:
   $3\cdot (2+5)=3\cdot 2+3\cdot 5=6+15=21$
   oder
   $3\cdot (2+5)=3\cdot 7=21$
2. Bemerkung: Multiplizieren mit 10
   Wenn man eine Zahl mit 10 multipliziert, ist das Ergebnis diese Zahl mit einer Null auf ihren rechten Seite geschrieben. Das haben wir in der einmaleins-Tabelle gesehen: $\textstyle 2\cdot 10=20\quad 3\cdot 10=30\quad 3\cdot 10=30\$ usw. Leicht denkt man dann, dass das Gleiche mit $\textstyle \ 15\cdot 10$ passiert. Tatsächlich ist $15\cdot 10$ gleich einer $15$ mit einer $0$ dahinter, also $15\cdot 10=150$.

Im Beispiel b ist es möglich, $30$ als Produkt von $3$ und $10$ zu schreiben. Es steht tatsächlich in der einmaleins-Tabelle, dass $\textstyle \ 3\cdot 10=30$ ist, also

$\textstyle \ 30=3\cdot 10$

Daher

$\textstyle \ 5\cdot 30=5\cdot 3\cdot 10=15\cdot 10$

(wir haben gerade eben im Beispiel a gesehen, dass $\textstyle \ 5\cdot 3=15$ ist).

Wir wir in der zweiten Bemerkung (Multiplizieren mit 10) gerade eben gelernt haben, gilt für $\textstyle 15\cdot 10$

$\textstyle 15\cdot 10=150$

Man kann also zusammenfassen:

$\textstyle \ 5\cdot 30=5\cdot 3\cdot 10=15\cdot 10=150$, also $\textstyle \ 5\cdot 30=150$.

Um Beispiel c zu lösen, können wir die erste Bemerkung (Multiplikation mit Klammern) benutzen:

$\textstyle \ 5\cdot 37=5\cdot (30+7)=5\cdot 30+5\cdot 7$ ist

$5\cdot 30=150$

wie wir eben im Beispiel b gesehen haben.

$\textstyle \ 5\cdot 7=35$

wie man aus der Einmaleins-Tabelle ablesen kann. Somit ist

$\textstyle \ 5\cdot 37=5\cdot (30+7)=5\cdot 30+5\cdot 7=150+35=185$,

also

$\textstyle \ 5\cdot 37=185$.

In der gleichen Weise und mit den gleichen Schritten kann man Beispiel d berechnen:

$\textstyle \ 4\cdot 37=4\cdot (30+7)=4\cdot 30+4\cdot 7=120+28=148$,

also

$\textstyle \ 4\cdot 37=148$.

Aber auch Beispiel e ist dann nicht so schwer, man soll einfach eine Null zum Ergebnis von d dazu schreiben, wie wir in der Bemerkung über Multiplikation mit 10 gelernt haben:

$\textstyle \ {\color {blue}4}{\color {red}\mathbf {0} }{\color {blue}\cdot 37}={\color {blue}168}{\color {red}\mathbf {0} }$

Wenn jetzt $37$ mit $45$ multipliziert wird, wie im Beispiel f, dann werden die folgenden Schritte gemacht:

${\begin{alignedat}{2}37\cdot 45&=37(40+5)\\&=37\cdot 40&&+37\cdot 5\\&=1480\ ^{\text{(Bsp. e)}}&&+185\ ^{\text{(Bsp. c)}}\end{alignedat}}$

(Wir haben hier die Ergebnisse aus den Beispielen e und c benutzt)

$1480+185$ ist

${\begin{array}{c|c|c|c|c}&1&4&8&0\\+&&1&8&5\\\hline &1&6&6&5\\\end{array}}$

wie wir schon bei der Addition gelernt haben. Also:

$37\cdot 45=1665$

Es gibt verschiedene Schreibweisen, die diesen Prozess beschreiben.

${\begin{array}{c|c|c|c|c}&45&\times &37&\\\hline &1&4&8&0\\+&&1&8&5\\\hline &1&6&6&5\\\end{array}}$	oder	(ohne Null) ${\begin{array}{c|c|c|c|c}&45&\times &37&\\\hline &1&4&8&\\+&&1&8&5\\\hline &1&6&6&5\\\end{array}}$	und
${\begin{array}{c|c|c|c|c}&&45&&\\&\times &37&&\\\hline &&1&8&5\\+&1&4&8&0\\\hline &1&6&6&5\\\end{array}}$	oder	${\begin{array}{c|c|c|c|c}&&45&&\\&\times &37&&\\\hline &&1&8&5\\+&1&4&8&\\\hline &1&6&6&5\\\end{array}}$

Wenn man Kommas hat, lässt man die Kommas und die Nullen am Anfang aus und macht die Multiplikation. Im Beispiel g ($\textstyle \ 0{,}45\cdot 0{,}000037$) haben wir insgesamt 8 Nachkommastellen (zwei bei $\textstyle \ 0{,}\overbrace {45} ^{2\ St.}$ und sechs bei $\textstyle \ 0{,}\overbrace {000037} ^{6\ Stellen}$, also 2+6=8 Stellen nach dem Komma insgesamt). Beim Ergebnis der Multiplikation ohne Kommas ($166{\color {red}5}$) fängt man dann mit der Ziffer rechts (hier ${\color {red}5}$) an und zählt nach links so viele Stellen, wie die gesamten Nachkommastellen (hier 8 Stellen). Dort muss beim neuen Ergebnis das Komma stehen. $1665$ hat aber nur vier Ziffer. Wenn die Zahl weniger Ziffer als die Nachkommastellen hat wie hier, schreibt man erst mehrere Nullen links der Zahl:

$000000001665\qquad \qquad 00000|\overbrace {0001665} ^{7\ Stellen}\qquad$Komma 7 Stellen nach links stellen → $0{,}0001665$

Daher:

$0{,}45\cdot 0{,}000037=0{,}0001665$

Wenn man Nullen am Ende der Zahlen hat, dann lässt man diese Nullen aus. Man macht die Multiplikation und schreibt dann wieder die ausgelassenen Nullen dazu. Im Beispiel h ($450\cdot 37000$) haben wir 4 Nullen (eine bei $650$ und drei bei $38000$). Also zum Ergebnis $1865$ schreibt man noch 4 Nullen dazu: $\textstyle \ 16650000$. Also $450\cdot 37000=18650000$.

Das Folgende Beispiel zeigt die Vorgangsweise genauer und Schritt zum Schritt:

Und noch ein Beispiel, diesmal mit zwei Zahlen mit jeweils drei Ziffern:

Division

Definition der Division

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses
Division	durch	:  (÷, /)	84      :      7      =	12
(dividieren, teilen)			Dividend : Divisor =	Quotient

Einfache Division mit Hilfe der Einmaleins-Tabelle

Mit diesem Vorgang kann man Divisionen durchführen, wenn der Divisor höchstens (also kleiner oder gleich) 10 ist und der Dividend höchsten das 10-fache des Divisors (also wenn der Divisor 4 ist, höchsten 40, wenn der Divisor 7 ist, höchstens 70 und so weiter.)

Zum Beispiel 17 : 5

Zeile des Divisors wählen	17 liegt zwischen 15 und 20 Beide Spalten wählen
Schauen, welche Zahlen oben in den Spalten stehen	Von beiden Zahlen (3 und 4) die kleinste wählen. Das ist das Ergebnis 17 : 5 = 3
Aber 3 mal 5 ist doch nicht 17	Es gibt einen Rest. Diesen berechnen wir dann: 3 mal 5 = 15 und 17−15=2 also 17 : 5 = 3 mit Rest 2 Man schreibt: 17:5=3 R 2

Der Haupt(vor)gang der Division

Der Vorgang der Division, wenn der Dividend eine größere Zahl ist, kann durch vier Schritte beschrieben werden:

1. ↓ Ziffer runter (ganz links anfangen)
2. ÷ was runter steht durch den Divisor dividieren (mit Hilfe der Einmaleinstabelle)
3. × das Ergebnis der Division mit dem Divisor multiplizieren
4. − dieses Produkt von dem, was "runter steht" subtrahieren. So berechnet man den Rest der Division (Schritt 2)

So einen Vorgang nennt man in Mathematik (und nicht nur) Algorithmus. Die vier Schritte (↓ ÷ × –) werden wiederholt (so was nennt man Iteration). Wenn der Rest null ist und es kein Ziffer mehr am Dividend gibt, dann hört man auf. Es gibt aber auch die Möglichkeit, dass der Rest nie Null wird. Dieser Fall wird später erklärt.

Am besten versteht man den Vorgang durch ein Beispiel (um ihn zu lernen, muss man selbstverständlich üben...). Probieren wir 792:3 zu berechnen:

Jetzt wird der Vorgang wiederholt!
Jetzt wird der Vorgang noch mal wiederholt!

Was aber man in der Tat schreibt, sieht doch anders aus! Man schreibt nur gewisse Schritte, der Rest macht man im Kopf oder als Nebenrechnung am Rand. Hier die Schritte, wie sie tatsächlich geschrieben werden:

Ein letztes Beispiel:

In diesem Fall sagt man, dass 842 durch 5 gleich 168 mit Rest 2 ist. Man schreibt 842:5=168 R 2. Der Rest muss allerdings immer kleiner als der Divisor sein (auch in den Zwischenschritten), sonst hat etwas nicht richtig geklappt. Die Division kann man allerdings weiterführen, wie wir bald lernen werden.

Dividend mit Nullen am Ende

Wenn der Dividend Nullen am Ende hat, kann man sich ein paar Schritte sparen. Schauen wir ein Beispiel:

Schauen wir jetzt, wie die richtige Regel lautet:

Man kann also die Division aufhören und die restlichen Nullen erst dann schreiben, wenn der Rest zum ersten Mal Null ist!

Wenn der Divisor auch Nullen am Ende hat, kann man vom beiden Divisor und Dividend so viele Nullen streichen, wie die Nullen des Divisors und erst dann die Division durchführen. Beispielsweise ist 7910000:400=79100:4 (in beiden Fällen ist das Ergebnis 19775). Warum das so ist, kann man erst verstehen, wenn man das Kürzen von Brüchen gelernt hat, daher lernen wir es hier zunächst einmal einfach so, als Regel...

Division mit Null in der Mitte des Ergebnisses

Ein Fehler, der oft vorkommt, ist die Nullen in der Mitte des Ergebnisses auszulassen. Im ersten Bild sieht man den richtigen Vorgang.   Für jede Ziffer des Dividenden, die runtergebracht wird, muss eine Ziffer im Ergebnis geschrieben werden!   Das richtige Ergebnis ist daher 2008. Im zweiten Bild sieht man den falschen Vorgang. Selbstverständlich ist 28 nicht gleich 2008 und daher ein falsches Ergebnis!

Division mit Null am Anfang des Ergebnisses

Was ist aber, wenn die Null (oder die Nullen) ganz am Anfang des Ergebnisses stehen? In diesem Fall spielt es keine Rolle, ob die Null da steht oder nicht. 059 bedeutet genau die gleiche Zahl wie 59 (allerdings auch genau wie 59,000 und 00059, auf gar keinen Fall aber wie 590 oder 59000...).   Wenn man Nullen vor dem Anfang einer Zahl oder nach der letzten Nachkommastelle schreibt, ändert sich die Zahl nicht.   47,03=00047,03=47,030000=0047,03000.   Das gilt allerdings nur für den Anfang der Zahl oder nach der letzten Nachkommastelle. Wenn man Nullen irgendwo in der Mitte der Zahl schreibt, dann hat man nicht mehr die gleiche Zahl. 47,03 ≠ 407,03 ≠ 470,03 ≠ 47,003    Alle diese Zahlen sind nicht gleich! Aus diesem Grund kann man am Anfang (und nur am Anfang) der Division mit den ersten zwei (oder drei und so weiter) Ziffern anfangen, wenn die erste kleiner als der Divisor ist. Dieser Vorgang wird im zweiten Bild dargestellt.

Dividend mit Komma (einfach)

Was ist, wenn der Divident schon Nachkommastellen hat? In diesem Fall wird die Division, wie wir sie bisher gelernt haben, mit einer Änderung durchgeführt:   Wenn zur nächsten Ziffer nach dem Komma gesprungen werden muss, dann muss man erst ein Komma im Ergebnis schreiben.   In unserem Fall ist es nicht wenn man die Ziffer 9 im Dividend erreicht. Das Komma muss geschrieben werden, erst bevor man die nächste Ziffer nach dem Komma (hier die Ziffer 2) runter bringen muss. Erst dann schreibt man das Komma und dann macht man die Rechnung (12:3) und dann schreibt man das Ergebnis dieser Rechnung (4) nach dem Komma. Es gibt kein anderes Komma in der Zahl (also auf gar keinen Fall irgendwo ein zweites Komma schreiben). Eine Bemerkung noch: Den letzten Rest haben wird hier mit (R) in Klammern geschrieben. Den Begriff Rest benutzt man eigentlich bei ganzzahligen Divisionen (mit Zahlen ohne Nachkommastellen). 0 ist hier der Teilrest der letzten Teildivision (12:4=3 R 0). Wenn bei einer Division mit Nachkommastellen im Ergebnis Teilrest 0 hat, kann man mit der Division aufhören. Das ist allerdings nur selten der Fall, wie wir gleich lernen werden.

Divisor mit Komma (einfach)

Was ist, wenn der Divisor Nachkommastellen hat, wie zum Beispiel in 236,2875:0,5? In diesem Fall wird das Komma sowohl im Divisor als auch im Dividenden so oft nach rechts verschoben, bis der Divisor keine (notwendige) Kommastelle mehr hat. In unserem Beispiel, wenn das Komma im Divisor (0,5) ein Mal nach rechts verschoben wird, bekommt man die Zahl 5, die keine Nachkommastellen hat. Das Komma wird dann auch im Dividenden (236,2875) ein Mal nach rechts verschoben (also der neue Dividend wird 2362,875 sein). Mit diesen neuen Zahlen kann man die Division ganz normal fortführen, wie im Bild am Rand. Der Prozess ist also:

Komma in Divisor verschieben, bis er keine Nachkommastelle hat:$0{\color {red},}5\ \to \ 0\underbrace {_{\color {red}{\xcancel {,}}}5{,}} _{1\ mal}...\ \to \ 5$ → Komma genauso oft (hier einmal) im Divident verschieben: $236{\color {red},}2875\ \to \ 236\underbrace {_{\color {red}{\xcancel {,}}}2{,}} _{1\ mal}875\ \to \ 2362{,}875\$ → Division mit den neuen Zahlen durchführen (siehe Bild)

Was ist, wenn der Dividend keine Nachkommastellen hat, beispielsweise 205:0,04?

In diesem Fall denkt man, dass ein Komma am Ende des Dividenden steht, und schreibt so viele Nullen wie notwendig nach dem Komma: 205=205,00 (allerdings gilt auch 205=205,00000 und so weiter). Dann wird der Vorgang wie vorher durchgeführt:

Komma im Divisor verschieben: $0{\color {red},}04\to 0\underbrace {_{\color {red}{\xcancel {,}}}04{,}} _{2\ mal}\to 4$ → Komma genauso oft (hier zweimal) im Dividenden verschieben, bis er keine Nachkommastelle hat:$205{\color {red},}00\ \to \ 205\underbrace {_{\color {red}{\xcancel {,}}}00{,}} _{2\ mal}...\ \to \ 20500\$ → Division mit den neuen Zahlen durchführen (siehe Bild)

Ein letztes Beispiel: 205:0,0004. Hier muss man das Komma sogar viermal verschieben:

Komma im Divisor verschieben: $0{\color {red},}0004\ \to \ 0\underbrace {_{\color {red}{\xcancel {,}}}0004{,}} _{4\ mal}...\ \to \ 4$\ → Komma genauso oft (hier zweimal) im Dividenden verschieben, bis er keine Nachkommastelle hat:$205{\color {red},}000000\ \to \ 205\underbrace {_{\color {red}{\xcancel {,}}}0000{,}} _{4\ mal}...\ \to \ 2050000\$ → Division mit den neuen Zahlen durchführen (siehe Bild)

Dividend ohne Komma, Ergebnis mit Komma (mit Null Rest)

Was ist, wenn die Division nicht genau aufgeht. wie zum Beispiel in 935:4?

		In diesem Beispiel ist es klar, dass ein Rest geben wird. Die Division kann man aber doch weiter fortsetzen, wie wir bei Zahlen mit Nachkommastellen schon gelernt haben. In diesem Beispiel können wir 935 als Zahl mit Nachkommastellen schreiben (freilich alle Nullen), wie wir schon gelernt haben: 935=935,00... Dann führen wir die Division in der gewöhnlichen Weise durch (siehe Bild). Allerdings kann man in diesem Fall die Nullen im Dividenden gar nicht schreiben, wie im Bild links unten zu sehen ist. In diesem Fall werden Nullen weiter unten geschrieben, bis der Teilrest irgendwann Null wird. Vorsicht aber: Wenn der Dividend zu Ende ist und die erste Null dazu benutzt wird, muss man ein Komma im Ergebnis schreiben!
			Diesen Prozess (weiter Nullen schreiben) kann man auch benutzen, wenn der Dividend zwar schon Nachkommastellen hat, der Teilrest am Ende aber doch nicht Null ist. In diesem Fall schreibt man Nullen weiter, selbstverständlich ohne ein zweites Komma im Ergebnis zu schreiben!

Dividend ohne Komma, Ergebnis mit Komma (periodisch)

Bisher war es fast immer in den Beispielen so, dass der Teilrest am Ende Null war. Das war kein Zufall, die Beispiele wurden einfach so gewählt, damit sie verständlicher sind. In der Regel ist der Teilrest keine genaue Zahl. Probieren wir es mit dem folgenden Beispiel:

Wie wir schon gelernt haben, wenn man das Ende der Zahl erreicht und keine Ziffer mehr hat, kann man doch die Division weiterführen: erst eine Null im Ergebnis schreiben und dann eine Null jedes Mal dazuschreiben, bis irgendwann der Teilrest Null wird. In unserem Fall hier passiert so etwas aber nicht. Wie man sieht, wiederholen sich die Zahlen 2 und 7 immer wieder und, wie man hoffentlich versteht, das wird immer so bleiben. Wir haben hier diese Wiederholung mit verschiedenen Farben dargestellt. Die wiederholte Zifferreihenfolge nennt man Periode. Man sagt, dass das Ergebnis von 938 durch 11 gleich 85 Komma 27 periodisch ist. Man bezeichnet die Periode mit einem Strich über der Zifferreihenfolge (oder mit einem Punkt, wenn es nur eine Ziffer ist). Man schreibt also: $938:11=85{,}{\overline {27}}$

Man braucht die Division nicht weiterführen. Wann kann man aber genau damit aufhören? Wenn man schon mit Null hinzufügen angefangen hat (passiert hier bei der letzten Ziffer der Zahl 938) und der gleiche Teildividend vorkommt, dann kann man aufhören, wie im Bild hier

Division Kombinationen

Hier finden wir ein paar weiterführende Beispiele zur Vertiefung der Kenntnissen.

Probieren wir erst die Division 3706,1:0,00007. Wenn der Divisor ein Komma hat (wie hier 0,00007), dann muss man das Komma sowohl im Divisor also auch im Dividenden so oft nach rechts verstellen, bis der Divisor keine Nachkommastellen mehr hat. Falls der Dividend dann nicht genügende Nachkommastellen hat, werden sie mit Nullen nachgefüllt. Daher ist 3706,1:0,00007 gleich so viel wie 370610000:7

3706,1:0,00007=370610000:7

Letztere Division führen wir auch im Bild durch. Wir fangen dann mit dem Hauptvorgang (in verkürzter Darstellung) an. Da die erste Stelle des Dividenden (3) kleiner als der Divisor ist, kann man weitere Ziffer des Dividenden benutzen (also 37), weil Nullen am Anfang des Ergebnisses (und nur dort) keine Rolle spielen. Diese zwei Stellen wurden mit Hellblau markiert. Da, wo die rote Stelle und der rote rechts-Pfeil im Bild ist, kann man weitere Nullen einführen, nachdem erst ein Komma im Ergebnis geschrieben wird (roter nach-oben-Pfeil und Komma im Ergebnis). Mit Lila (um dem Teildividenden 30) wird darauf aufmerksam gemacht, dass das Ergebnis doch periodisch ist (also der Teildividend 30 und alle andere Teildividenten, die nach ihm kommen, in der gleichen Reihe immer wiederholt vorkommen). Die Periode, wie im Ergebnis wieder mit Lila notiert, ist die Zifferfolge 428591.

Da man aber die Periode im Ergebnis erst nach dem Komma notiert wird, schreibt man nicht

$3706,1:0,00007=5295{\overline {4285{,}91}}\$ (falsch), sondern

$3706,1:0,00007=52954285{,}{\overline {914285}}\$ (richtig).

Im vorherigen Beispiel haben wir eine Division durch 11 gesehen. Da bestand die Periode aus zwei Ziffern (27). Im letzten Beispiel (Division durch 7) bestand die Periode aus sechs Ziffern (914285). Bei einer anderen Division (durch 4), gab es wieder keine Periode. Es kann also eine Periode geben oder nicht, und sie kann lang oder kurz sein. Im folgenden Beispiel (938:23) haben wir die Periode nicht mal angegeben, da sie schon aus 22 Ziffern(!) besteht. Es gibt einen Beweis dafür, dass wenn der Divisor und der Dividend ganze Zahlen sind (oder sein können), immer eine Periode entsteht (also eine wiederholte Reihenfolge von Ziffern nach dem Komma) oder ein Teilrest Null (also die Division kann aufhören). Diese Periode kann sehr lang sein, es gibt sie aber in diesem Fall immer.

Im folgenden Beispiel lernen wir allerdings auch dazu genauer, wie man die Division durchführt, wenn der Divisor größer als 10 ist. Wir haben schon eine solche Division gesehen, aber noch nicht erklärt, wie das funktioniert.

Grundsätzlich gibt es hier nichts Neues. Man soll wieder die Grundschritten durchführen:

↓ Ziffer runter (ganz links anfangen)

÷ was runter Steht durch den Divisor dividieren ("wie oft der Divisor in den Teildividenden hineinpasst")

× das Ergebnis der Division mit dem Divisor multiplizieren

− dieses Produkt von dem, was "runter steht" subtrahieren.

Nun aber werden diese Schritte irgendwo am Rand durchgeführt und jeweils unter dem Teildividenden das Ergebnis der Subtraktion am Ende geschrieben.

Schritt ↓ Ziffer runter: Weil die erste Ziffer im Dividend (9) kleiner als der Divisor (23) ist, nehmen wir am Anfang die ersten zwei Ziffer des Dividenden (93)

Schritt ÷ dividieren: 23 passt in 93 viermal hinein (das kann man allerdings bei größeren Zahlen nur raten und ausprobieren). Wie erste Ziffer des Ergebnisses wird daher 4 sein.

Schritt × multiplizieren: Die letzte Ziffer des Ergebnisse (4) wird mit dem Divisor multipliziert: 4×23=92.

Schritt − subtrahieren: Das Ergebnis der Multiplikation (92) wird aus dem vorläufigen Teildividenden (93) subtrahiert (93−92=1). Allein das Ergebnis der Subtraktion (hier 1) wird dann unter den Teildividenden geschrieben. Im Bild haben wir allerdings die zwei letzten Schritten am Rand links zusammengefasst (93−4×23=1).

Diese Schritte werden dann wiederholt, bis man irgendwann die Periode entdeckt. Hier haben wir allerdings schon ziemlich bald aufgehört (wie schon erwähnt, ist die Periode in diesem Beispiel sehr lang...).

Im folgenden Beispiel ist der Divisor wieder größer als 10, wir haben aber hier die Teilschritte des Hauptvorgangs (↓ ÷ × −) nicht am Rand geschrieben. Die Division lautet 4,52:1,3, man soll also erst das Komma verschieben: 4,52:1,3=45,2:13. Letztere Division wird im Bild gezeigt. Wieder muss man mit zwei Ziffern anfangen. Sofort nach der ersten Ziffer im Ergebnis muss man ein Komma schreiben (roter Pfeil). Und wieder gibt es eine Periode (wenn der Teildividend 100 wiederholt wird), die Ziffernfolge 769230. Die Periode besteht hier (wie bei der Division durch 7 am Anfang dieses Teilkapitels) aus sechs Ziffern. Also $\ 4,52:1,3=3{,}4{\overline {769230}}$. Hier ist zu beachten, dass nicht alle Ziffern nach dem Komma die Periode sind! Die Periode fängt in diesem Fall erst nach der ersten Nachkommastelle an.

Wenn allerdings die Division 0,0452:13 durchgeführt wird, muss man im Ergebnis schon mit Null und Komma anfangen (Bild links)! Der Rest des Vorgangs bleibt unverändert. Vorsicht aber: in diesem Fall (wenn Komma schon am Anfang steht), darf man Nullen nicht auslassen! Die Periode allerdings fängt in diesem Fall noch weitere Stellen nach dem Komma an: $0{,}0452:13=0{,}00034{\overline {769230}}$.

Bei der Division 330,103:11 (links) finden wir noch ein paar Neuigkeiten. Die Periode besteht zwar wieder aus zwei Ziffern wie in der vorherigen Division durch 11, diesmal sind es aber die Ziffern 36 (und nicht 27). Es gibt in dieser Division einige Nullen dazwischen, die man selbstverständlich NICHT auslassen darf und dazu ein Komma unter diesen Nullen.

Bei der Division 391,204:11 (rechts) stellt man fest, dass die Division durch 11 sogar auch genau ausgehen kann (das stimmt ja für alle Divisoren, die ganzzahlig, also ohne Komma, sind). Wenn der Teilrest Null ist, ist der Vorgang fertig. Wann die Division durch bestimmte Zahlen genau aufgeht, lernt man im Kapitel über Teilbarkeit.

Im letzten Beispiel können wir sehen, dass die Periode auch nur eine Ziffer sein kann (hier 6). In diesem Beispiel fängt die Periode wieder erst an der dritten Nachkommastelle an. Man schreibt: $7,43:3=2,47{\dot {6}}$

Punktrechnungen mit 10, 100, 1000 und so weiter

• Wenn man eine Zahl mit 10, 100, 1000 und so weiter multipliziert, dann verschiebt sich das Komma der Zahl einfach nach rechts (die Zahl wird größer), so oft, wie es Nullen gibt:

3,45 · 10 = 34,5    (Mal 10; in 10 gibt es eine Null, Komma wird einmal nach rechts verschoben)

54 · 10000 = 54,0000 · 10000 = 540000    (Mal 10000; in 10000 gibt es vier Nullen, Komma wird 4 Mal nach rechts verschoben; Allerdings gibt es kein Komma am Ende der Zahl 54; man schreibt ein Komma am Ende der Zahl und dazu nach dem Komma so viele Nullen, wie man will, und schiebt dann das Komma)

0,008 · 100 = 0,8    (Mal 100; in 100 gibt es 2 Nullen, Komma wird 2 Mal nach rechts verschoben)

• Wenn man eine Zahl mit 10, 100, 1000 und so weiter dividiert, dann verschiebt sich das Komma der Zahl einfach nach links (die Zahl wird kleiner), so oft, wie es Nullen gibt:

3,45:10 = 0,345    (Durch 10; in 10 gibt es eine Null, Komma wird einmal nach links verschoben; allerdings gibt es links vor 3,4 keine Null, man schreibt also links von der Zahl so viele Nullen, wie man will, und schiebt dann das Komma)

54:10000 = 0,0054    (Durch 10000; in 10000 gibt es 4 Nullen, Komma wird 4 Mal nach links verschoben; allerdings gibt es links vor 54 kein Komma, man schreibt also links von der Zahl ein Komma und so viele Nullen, wie man will, und schiebt dann das Komma)

0,008:100 = 0,00008    (Durch 10; in 10 gibt es eine Null, Komma wird 1 Mal nach links verschoben; allerdings muss man zuerst am Ende der Kommazahl weitere Nullen schreiben)

900000:100 = 9000,00 = 9000    (Durch 100; in 100 gibt es 2 Nullen, Komma wird 2 Mal nach links verschoben; da es kein Komma am Ende der Zahl gibt, muss man erst das Komma schreiben)

Textaufgaben zu den Grundrechenarten

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses
Addition	plus	+	$2$        $+$      $7$      $=$	$9$
(addieren, erhöhen)			Summand $+$ Summand $=$	Summe
Subtraktion	minus	−	$65$      $-$      $22$      $=$	$43$
(subtrahieren, reduzieren, vermindern, abziehen)			Minuend $-$ Subtrahend $=$	Differenz
Multiplikation	mal	⋅  (×)	$9$      $\cdot$      $13$      $=$	$117$
(multiplizieren, vervielfachen, -fach)			Faktor  ⋅  Faktor $=$	Produkt
Division	durch	:  (÷, /)	$84$      $:$      $7$      $=$	$12$
(dividieren, teilen)			Dividend $:$ Divisor $=$	Quotient

Mit den Grundrechenarten kann man auch Textaufgaben bilden. Bei diesen Aufgaben ist in der Regel die Bedeutung der Wörter nicht so wichtig, wie der Aufbau des Satzes:

• Dividieren Sie die Differenz von 125 und 20 mit der Summe von 4 und 3.

Schauen wir mal, wie der Satz aufgebaut ist. Erst steht, dass man dividieren muss (also durch machen). Was muss man aber dividieren? Was steht nach dem Wort dividieren? Die Zahlen 125 und 20? NEIN! Nach dem Wort dividieren (durch machen) steht das Wort Differenz! Man muss also erst eine Differenz berechnen! Welche Differenz? Die Differenz von 125 und 20(was nach dem Wort Differenz steht)! Das steht ja auch da! Die Differenz (Minus) von 125 und 20 ist 125−20=105. Diese Differenz muss man durch irgendwas dividieren. Ist das durch 4, durch 3 oder doch was anderes? Doch was anderes! Die Differenz muss man mit der Summe (Plus machen) dividieren. Man muss also erst eine Summe berechnen, die Summe von 4 und 3 (was nach dem Wort Summe steht), 4+3=7. Man soll also die Differenz (105) durch die Summe (7) dividieren:

105:7=15. 15 ist also die Antwort zur Aufgabe!

Vorrang der Rechenarten

Grundrechenartenvorrang

Bei einer Rechnung muss die Reihenfolge der Rechnungen klar sein, sonst ist das Ergebnis nicht eindeutig:

$6+3-7+5$:

• Wenn man von links nach rechts liest, dann: $\ 6+3=9,\ 9-7=2,\ 2+5=7\quad$ also Ergebnis 7.
• Wenn man von rechts nach links liest, dann: $\ {\overleftarrow {{\color {red}12}=7+5}},\ {\overleftarrow {{\color {lime}9}=3-{\color {red}12}}},\ {\overleftarrow {15=6+{\color {lime}9}}}\quad$ also Ergebnis 15.

Das Ergebnis ist nicht das Gleiche! In den meisten Sprachen der Welt fängt man links an. Dann ist das richtige (und eindeutige) Ergebnis 7. Nur bei Addition oder Multiplikation spielt die Leserichtung und allgemein die Reihenfolge keine Rolle:

$6+5+11=5+6+11=11+5+6=5+11+6=22$

$2\cdot 4\cdot 5=4\cdot 2\cdot 5=2\cdot 5\cdot 4=40$

In diesem Buch wird die Deutsche Leserichtung benutzt, also von links nach rechts.

Was ist, wenn man Strich- und Punktrechnungen gleichzeitig hat? Spielt hier die Reihenfolge wieder keiner Rolle, wie bei der Addition oder der Multiplikation?

$2+3\cdot 4$

Machen wir die Rechnung einfach von links nach rechts, ist das Ergebnis: $2+3=5\ \to \ 5\cdot 4=20$

Ändern wir die Reihenfolge der Multiplikation: $2+4\cdot 3$

und machen wir die Rechnung einfach von links nach rechts, bekommen wir ein anderes Ergebnis: $2+4=6\ \to \ 6\cdot 3=18$

Es gilt auch:

• Wenn man erst die Strichrechnung macht, ist das Ergebnis: $2+3=5\ \to \ 5\cdot 4=20$
• Wenn man erst die Punktrechnung macht, ist das Ergebnis: $3\cdot 4=12\ \to 2+12=14$

Das Ergebnis ist wieder unterschiedlich.Ein unterschiedliches Ergebnis kommt auch dann vor, wenn die Reihenfolge bei der Addition geändert wird und die Multiplikation erst gemacht wird:

$2+3\cdot 4\$ und $\ 3+2\cdot 4$

Hier haben wir die Reihenfolge bei der Addition geändert (einmal steht 2+3 und dann 3+2). Machen wir in beiden Fällen erst die Multiplikation:

$2+3\cdot 4\ =2+12=14\$ und $\ 3+2\cdot 4=3+8=11$

Das Ergebnis ist wieder unterschiedlich. Wenn wir aber einen mathematischen Ausdruck haben, wollen wir ein eindeutiges Ergebnis. Damit das Ergebnis eindeutig ist, muss es eine Regel geben. In Mathematik haben die Punktrechnungen (mal und durch) immer Vorrang vor den Strichrechnungen (Plus und Minus). Man muss zuerst die Punktrechnungen machen und dann die Strichrechungen. Also ist hier 14 das richtige Ergebnis. Wenn es also in einer Rechnung Strich- und Punktrechnungen gibt, dann muss man zuerst die Punktrechnungen machen!

Wenn es aber eine Klammer gibt, dann muss man erst die Rechnung in der Klammer machen:

$(2+3)\cdot 4=5\cdot 4=20\$ Hier ist das Ergebnis doch $20$

$2+(3\cdot 4)=2+12=14\$ ...und hier ist das Ergebnis wieder $14$.

Wenn in einem mathematischen Ausdruck mehrere Rechenarten vorkommen, dann muss eine Regel gelten, damit das Ergebnis eindeutig ist. Die grundlegende Regel lautet:

Klammer vor Punkt vor Strich.

(Zu Erinnerung: Punktrechnungen sind mal und durch, Strichrechnungen sind plus und minus)

Wenn es wiederum innerhalb einer Klammer mehrere Rechnungen gibt, dann muss man die Klammer erst machen und in der Klammer an die Regeln halten:

$5+36:(3\cdot 5-6)-(56:7-2)\cdot 3=?$

Unterstreichen wir zuerst die Rechnungen in den Klammern:

$5+$	$36:$	${\underline {({\underline {3\cdot 5}}-6)}}\ -$	${\underline {({\underline {56:7}}-2)}}$	$\cdot 3$	$=$	In beiden Klammern muss man zuerst die Punktrechnung machen
		$15-6\quad$	$8-2$			und dann die Strichrechnung in Klammer
		$9$	$6$			Man kann also die Klammer durch das jeweilige Ergebnis ersetzen

$5+$	$36:$	${\cancelto {9}{(3\cdot 5-6)}}\ -$	${\cancelto {6}{(56:7-2)}}$	$\cdot 3=$
$5+$	$36:$	$9-$	$6$	$\cdot 3=$	Kompakter geschrieben ist die Rechnung jetzt:

$5+36:9-6\cdot 3\qquad \qquad$ Hier muss man erst die Punktrechnungen machen

$5+{\cancelto {4}{36:9}}-{\cancelto {18}{6\cdot 3}}=$

$5+4-18=-9$

Hier das Ganze noch einmal übersichtlicher und in einer Animation:

Alle Schritte kompakt dargestellt: ${\begin{array}{c}5+36:\underbrace {(\underbrace {3\cdot 5} _{15}-6)} _{9}-\underbrace {(\underbrace {56:7} _{8}-2)} _{6}\cdot 3=\\5+\underbrace {36:9} _{4}-\underbrace {6\cdot 3} _{18}=\\5+4-18=-9\end{array}}$

Vorrang mit Klammern in Klammern

$5+6\cdot 7-55:$	$(21-4\cdot 8)$	$-3\cdot$	$[7+$	$2\cdot (6\cdot 3-39:3)]$	$-57$	$=$	In der großen Klammer hat die kleine Klammer Vorrang (Klammer vor Punkt vor Strich)
	↓		$7+$	$2\cdot (18-13)$			In der kleinen Klammer erst Punkt und dann Strichrechnung
	↓		7   +   $2\cdot 5$				Kleine Klammer durch ihr Ergebnis in der großen Klammer ersetzen
	$21-32$		$7$   +   $10$				In den verbliebenen Klammern erst Punkt- und dann Strichrechnungen
	$-11$		$17$				Man kann also die Klammer durch das jeweilige Ergebnis ersetzen

${\begin{array}{c}5+6\cdot 7-55:{\cancelto {21-32=-11}{(21-4\cdot 8)}}-3\cdot \underbrace {{\Bigl [}7+{\color {blue}\overbrace {2\cdot {\color {red}({\cancelto {18}{6\cdot 3}}-{\cancelto {13}{39:3)}}}} ^{2\cdot {\color {red}{\cancelto {5}{(18-13)}}}=\ \ 10}{\color {black}{\Bigr ]}}}} _{7+{\color {blue}10}=17}-57=\\\\5+{\cancelto {42}{6\cdot 7}}-{\cancelto {-5}{55:(-11)}}+{\cancelto {51}{3\cdot 17}}-57\\\\5+42+5-51-57=-56\end{array}}$

(an Plus-Minus Regeln halten!)

(an Plus-Minus Regeln halten!)

Bruchrechnungen

Was ist ein Bruch

Bruch:    $\textstyle {\begin{array}{ccc}10&\leftarrow {\text{Zähler}}\\{\boldsymbol {-}}&\leftarrow \mathrm {Bruchstrich} \\5&\leftarrow \mathrm {Nenner} \end{array}}$    

Es gilt:   $\textstyle {\frac {10}{5}}=10:5=2$   (Ein Bruch ist wie eine Division)

Unterschied: Ein Bruch ist eine Zahl. Eine Division ist eine Rechenart zwischen zwei Zahlen.

Echter Bruch: Wenn der Nenner größer als der Zähler ist: $\textstyle {\frac {5}{11}}$

Unechter Bruch: Wenn der Zähler größer als der Nenner ist: $\textstyle {\frac {11}{5}}$

Gleichnamige Brüche: Brüche, die den gleichen Nenner haben (z.B. $\textstyle {\frac {10}{5}}$,  $\textstyle {\frac {3}{5}}$ aber NICHT $\textstyle {\frac {5}{10}}$ und $\textstyle {\frac {5}{9}}$, wo der Zähler gleich ist, oder $\textstyle {\frac {10}{5}}$ und $\textstyle {\frac {5}{9}}$)

Gemischte Zahlen

Eine gemischte Zahl besteht aus einer natürlichen Zahl und einem echten Bruch:  $\textstyle 6{\frac {4}{5}}$

Gemischte Zahl in unechten Bruch umwandeln

Um eine gemischte Zahl in einen Bruch umzuwandeln, multipliziert man die natürliche Zahl mit dem Nenner des Bruches und addiert das Ergebnis zum Zähler. Das neue Ergebnis ist dann der Zähler des neuen Bruches, der Nenner bleibt der gleiche:

$6{\frac {4}{5}}={\frac {6\cdot 5+4}{5}}={\frac {34}{5}}$

Unechten Bruch in gemischte Zahl umwandeln

Um einen unechten Bruch in eine gemischte Zahl umzuwandeln, dividiert man den Zähler mit dem Nenner (ohne Nachkommastellen). Das Ergebnis der Division ist der „Zahlteil“ der gemischten Zahl, der Rest ist der Zähler des „Bruchteils“, der Nenner bleibt der gleiche:

    (siehe Division)

Folgendes Beispiel setzt die Anwendung eines Taschenrechners voraus:

${\frac {1895}{23}}=?\qquad \qquad {\begin{array}{rrl}1895&:{\boldsymbol {2}}3&={\color {red}{\boldsymbol {8}}2}{,}\dots \\\ {\color {red}{\boldsymbol {8}}2}&\cdot \ {\boldsymbol {2}}3&={\color {YellowOrange}1886}\\1895&-{\color {YellowOrange}1886}&={\color {blue}{\boldsymbol {9}}}\end{array}}\qquad \qquad {\text{ also }}\quad {\frac {1895}{23}}={\color {red}{\boldsymbol {8}}2}{\frac {\color {blue}{\boldsymbol {9}}}{{\boldsymbol {2}}3}}$

Eintausend-achthundert-fünfundneunzig Dreiundzwanzigstel sind so viel wie zweiundachtzig Ganzen und neun Zwanzigstel.

Das Ergebnis der Division 1895:23 mit dem Taschenrechner ist 82 Komma einige Nachkommastellen. Dieses Ergebnis ohne Nachkommastellen (82) wird die ganze Zahl in der gemischte Zahl sein. Das Ergebnis ohne Nachkommastellen (82) wird dann mit den Nenner (hier 23) multipliziert: 82·23=1886. Dieses Produkt (1886) wird dann vom Zähler (1895) subtrahiert: 1895-1886=9. Diese Differenz (9) stellt den neuen Zähler in der gemischten Zahl dar, der Nenner bleibt unverändert (23).

Der Prozess also mit Anwendung eines Taschenrechners könnte so aussehen:

${\frac {1895}{23}}=?$

Division mit dem Taschenrechner durchführen (1895:23=82 Komma einige Nachkommastellen). Ergebnis nach dem Gleichzeichen samt Bruchstrich und Nenner (23) schreiben:

${\frac {\color {red}1895}{23}}={\color {red}81}{\frac {?}{\color {red}23}}$

Die Diagonale (hier oben mit roten Zahlen markiert:) Zähler links (1895) minus ganze Zahl (81) mal Nenner rechts (23) wie im folgenden benutzen und Ergebnis in den Zähler rechts schreiben:

$1895-81\cdot 23={\color {red}9}$

also

${\frac {1895}{23}}=81{\frac {\color {red}9}{23}}$

Erweitern und Kürzen

Erweitern

Erweitern ist, wenn man sowohl Zähler als auch Nenner eines Bruches mit der gleichen Zahl multipliziert. Der neue Bruch bleibt dann doch gleich:

${\frac {4}{7}}={\frac {4\cdot 5}{7\cdot 5}}={\frac {20}{35}}$

Bruchkürzen

Kürzen ist, wenn man sowohl Zähler als auch Nenner eines Bruches mit der gleichen Zahl dividiert. Der neue Bruch bleibt dann doch gleich:

${\frac {12}{8}}={\frac {12:4}{8:4}}={\frac {3}{2}}$

In all diesen Fällen arbeitet man mit natürlichen Zahlen (positive Zahlen ohne Komma).

Erklärung des Erweiterns und des Kürzens

7 2         5

Vergleichen wir die beiden Bilder. Im ersten Bild wird das Ganze im $5$ geteilt, zwei Teile davon werden dunkel dargestellt. Das ist also eine Repräsentation des Bruches $\textstyle \ {\frac {2}{5}}$. Im zweiten Bild wird das Ganze nicht nur in $5$ (waagerecht) sondern auch in $7$ (senkrecht) geteilt. Dadurch entstehen im Ganzen $\ 5\cdot 7=35\$ kleine "Quadrate". Jedes kleines Quadrat ist daher $\textstyle \ {\frac {1}{35}}\$ des Ganzen. Die dunkle Region ($\textstyle \ {\frac {2}{5}}$) beinhaltet allerdings $\ 2\cdot 7=14\$ solche "Quadrate" also $\textstyle \ {\frac {14}{35}}$. Man folgt daraus, dass $\textstyle \ {\frac {2}{5}}={\frac {14}{35}}\$ ist. Man hat in diesem Fall sowohl den Zähler als auch den Nenner mit der gleichen Zahl (hier $7$) multipliziert: $\textstyle \ {\frac {2}{5}}={\frac {2\cdot 7}{5\cdot 7}}={\frac {14}{35}}\$. Diesen Prozess nennt man erweitern.

Der Gegenprozess ist dann das Kürzen. Im ersten Bild wird das Ganze in $5$ Zeilen und $7$ Spalten also insgesamt in $\ 7\cdot 5=35\$ kleine "Quadrate" geteilt (das könnte selbstverständlich eine andere Austeilung sein). Die blaue Region ist $\ 3\cdot 5=15\$ solche Teile, also $\textstyle \ {\frac {15}{35}}$. Wenn man jetzt die waagerechte Austeilung (in Fünf Zeilen geteilt) entfernt (zweites Bild), dann ist das ganze nur in $7$ (Spalten) geteilt, wobei jetzt die blaue Region $3$ Spalten davon ist also $\textstyle \ {\frac {3}{7}}$. In diesem Fall haben wir sowohl Zähler als auch Nenner durch die gleichen Zahl (hier $5$) dividiert: $\textstyle \ {\frac {15}{35}}={\frac {15:5}{35:5}}={\frac {3}{7}}$. Diesen Prozess nennt man kürzen.

Strich und Punkt Bruchrechnungen

Strichbruchrechnungen

Wenn man zwei Brüche addiert oder subtrahiert, dann muss man auf den Nenner aufpassen:

Brüche mit gleichem Nenner:

${\frac {5}{4}}+{\frac {2}{4}}={\frac {5+2}{4}}={\frac {7}{4}}$

Brüche mit unterschiedlichen Nennern: Zähler und Nenner des ersten Bruches mit Nenner des zweiten erweitern (blaue Pfeile) und entsprechend für den zweiten Bruch (rote Pfeile)!

$={\frac {5\cdot 3}{4\cdot 3}}+{\frac {2\cdot 4}{3\cdot 4}}$$\textstyle \color {CadetBlue}{\left(={\frac {5\cdot 3+2\cdot 4}{3\cdot 4}}\right)}$$={\frac {15}{12}}+{\frac {8}{12}}={\frac {15+8}{12}}={\frac {23}{12}}$

Dabei ist es nicht wichtig, ob man minus oder plus zwischen den Brüchen hat. Allein der Nenner (ob er der gleiche oder nicht ist) spielt einer Rolle.

Erklärung der Strichbruchrechnungen

Wenn man den gleichen Nenner hat, ist es leicht mit einer Figur zu verstehen, warum die angegebene Regel gilt. Man kann sehen:

wenn zwei gleiche Schokoladentafeln in 7 geteilt werden und von einer Schokoladentafel 3 Teile (drei Siebtel) und von der anderen 2 Teile (zwei Siebtel) genommen werden, hat man insgesamt 5 Teile (also fünf Siebtel).

Was ist aber, wenn man nicht den gleichen Nenner hat (ungleichnamige Brüche), wie z.B. mit $\textstyle \ {\frac {2}{5}}+{\frac {3}{7}}$ ?

• 
• 

Das Ergebnis ist:

$\ {\frac {2}{5}}+{\frac {3}{7}}={\frac {2\cdot 7+5\cdot 3}{5\cdot 7}}={\frac {29}{35}}.$

Um dies zu zeigen, haben wir das erste Rechteck horizontal in 5 Teile geteilt und das zweite senkrecht in 7. Wir teilen jetzt dazu die erste Figur auch in 7 senkrechte Teile und die zweite in 5 horizontale:

• 
• 

Wir haben in jedem der beiden (gleichen) Rechtecken 5 mal sieben, also 35 kleine Quadrate. Jedes kleines Quadrat in den neuen Figuren ist daher $\textstyle \ {\frac {1}{35}}\$ des Ganzen. Wie man sehen kann, sind die $\textstyle {\frac {2}{5}}\$ gleich so viel wie $\textstyle \ {\frac {2\cdot 7}{5\cdot 7}}={\frac {14}{35}}\$ und die $\textstyle \ {\frac {3}{7}}\$ gleich so viel wie $\textstyle \ {\frac {3\cdot 5}{7\cdot 5}}={\frac {15}{35}}.\$ Da wir jetzt gleichnamigen Brüchen haben, kann man die Zähler addieren:

${\frac {2}{5}}+{\frac {3}{7}}={\frac {2\cdot 7}{5\cdot 7}}+{\frac {3\cdot 5}{7\cdot 5}}={\frac {14}{35}}+{\frac {15}{35}}={\frac {14+15}{35}}={\frac {29}{35}}$

Aus unserer alltäglichen Erfahrung können wir vermuten, dass wir diesen Vorgang auch bei allen anderen Paaren von ungleichnamigen Brüchen übertragen können (wenn auch mit viel mehr Aufwand für größeren Nennern). Das können wir dann auch auf mehrere Brüche übertragen, da wir den Vorgang erst am ersten Paar anwenden können und dann mit dem Ergebnis mit dem nächsten Bruch arbeiten können usw. Dies gilt auch für die Subtraktion von Brüchen (wenn das Ergebnis positiv ist).

Punktbruchrechnungen

Bei einer Multiplikation zwischen zwei Brüchen multipliziert man Zähler mit Zähler und Nenner mit Nenner (Oben mal Oben, Unten mal Unten):

${\frac {5}{4}}\cdot {\frac {3}{7}}={\frac {5\cdot 3}{4\cdot 7}}={\frac {15}{28}}$

Bei der Division von zwei Brüchen multipliziert man den ersten Bruch mit dem Kehrwert des zweitens Bruches:

${\frac {5}{4}}:{\frac {3}{7}}={\frac {5}{4}}\cdot {\frac {7}{3}}={\frac {5\cdot 7}{4\cdot 3}}={\frac {35}{12}}$   ($\textstyle {\frac {7}{3}}$ ist der Kehrwert von  $\textstyle {\frac {3}{7}}$)

Hier spielt der Nenner keine Rolle (im Gegenteil zu den Strichrechnungen).

Erklärung der Punktbruchrechnungen

Doppelbrüche

Ein Doppelbruch ist wie die Division zwischen zwei Brüchen. Der Bruch oben wird durch den Bruch unten dividiert, also mit dem Kehrwert des Bruches unten multipliziert:

${\dfrac {\ \ {\frac {7}{12}}\ \ }{\frac {3}{20}}}={\frac {7}{12}}:{\frac {3}{20}}={\frac {7}{\cancelto {3}{12}}}\cdot {\frac {\cancelto {5}{20}}{3}}={\frac {35}{9}}$

Arbeiten mit ganzen Zahlen und Brüchen

Die Rechnungen mit ganzen Zahlen und Brüchen sind leicht, wenn man den vorherigen Stoff schon verstanden hat.

Strichrechnungen

Um eine ganze Zahl in einen Bruch umzuwandeln, reicht das Produkt der ganzen Zahl mit dem Nenner des Bruches als Zähler im Bruch zu schreiben:

$3={\frac {5\cdot 3}{5}}={\frac {15}{5}}$

Das sollte schon klar sein, da 15:5=3 ist... Um das zu veranschaulichen reicht es 3 ganzen jeweils in 5 geteilt nebeneinander zu stellen. Dann werden genau 3×5=15 Fünftel aufgezählt!

Hat man einmal die ganze Zahl als (gleichnamigen) Bruch, kann man auch eine entsprechende Strichrechnung durchführen, z.B.:

$3+{\frac {2}{7}}={\frac {3\cdot 7}{7}}+{\frac {2}{7}}={\frac {23}{7}}\qquad \qquad 5-{\frac {5}{9}}={\frac {5\cdot 9}{9}}-{\frac {5}{9}}={\frac {40}{9}}$

Punktrechnungen

Genau so leicht ist die entsprechende Multiplikation. Im ersten Bild werden zwei Fünftel dargestellt und diese werden 4 mal nebeneinander dargestellt. Insgesamt sind es daher 4×2=8 Fünftel.

$4\cdot {\frac {2}{5}}={\frac {4\cdot 2}{5}}={\frac {8}{5}}$

Um das Produkt einer ganzen Zahl mit einem Bruch zu berechnen, reicht es das Produkt der ganzen Zahl mit dem Zähler des Bruches in einem neuen gleichnamigen Bruch zu schreiben.

Die Division ist dann auch leicht:

$4:{\frac {3}{13}}=4\cdot {\frac {13}{3}}={\frac {52}{3}}\ (=17{\frac {1}{3}})$

Um den Quotient einer ganzen Zahl durch einem Bruch zu berechnen, reicht es das Produkt der ganzen Zahl mit dem Kehrwert des Bruches zu berechnen.

Primfaktorzerlegung

Was sind Primzahlen

Primzahlen sind die natürlichen Zahlen (Zahlen ohne Komma und Minus), die nur durch 1 und sich selbst geteilt werden können. (teilbar: dividieren, ohne dass eine Kommazahl entsteht)

	2	3	4	5	6	7	8	9	10	11	12	13
geht auch durch			2		2 3		2 4	3	2 5		2 3 4 6
Prim- zahl	✔	✔	✘	✔	✘	✔	✘	✘	✘	✔	✘	✔

Z.B.:

2 ist nur durch 2 und 1 teilbar und daher eine Primzahl.

3 ist nur durch 3 und 1 teilbar und daher eine Primzahl.

4 ist nur durch 4 und 1, aber auch durch 2 teilbar und daher keine Primzahl.

5 ist nur durch 5 und 1 teilbar und daher eine Primzahl.

6 ist nur durch 6 und 1, aber auch durch 2 und 3 teilbar und daher keine Primzahl.

usw.

Was bedeutet in diesen Sätzen "teilbar"? Eine Zahl ist durch eine andere Zahl teilbar, wenn das Ergebnis der Division keine Nachkommastellen enthält.

Nehmen wir die Zahl 5.

$5:1=5$

$5:2=2{,}5$

$5:3=1{,}{\dot {3}}$ 

$5:4=1{,}25$

$5:5=1$

Dividiert man 5 durch jede größere natürliche Zahl (also: 6,7,8…), erhält man als Ergebnis eine Kommazahl kleiner als 1 (also Null-Komma-irgendwas). Beispielsweise:

$5:6=0{,}8{\dot {3}}$

Teilbar ist die Zahl 5 also nur durch eins (5:1=5) und sich selbst (5:5=1). Da bei unserem Beispiel alle anderen Ergebnisse ein Komma enthalten ist die Zahl 5 eine Primzahl.

Für 6 hingegen ist das nicht der Fall. 6 ist selbstverständlich durch 1 und 6 teilbar, aber eben auch durch 2 (6:2=3) und durch 3 (6:3=2). Daher ist 6 KEINE Primzahl.

Die ersten Primzahlen sind also 2, 3, 5, 7, 11, 13, 17, 19, 23 ...

Faktor ist ein Teil einer Multiplikation.

Primfaktorzerlegung (PFZ) bedeutet daher, eine Zahl als Produkt von Primzahlen auszudrücken (die dann Faktoren sind; Primzahlen die auch Faktoren sind, nennt man Primfaktoren; wenn man eine Zahl in Primfaktoren zerlegt, hat man die PFZ).

Primfaktorzerlegung Vorgangsweise

Nehmen wir die Zahl 7800. Wir versuchen sie durch die Primzahlen der Reihe nach und soweit es jedes Mal geht zu dividieren. Die erste Primzahl ist 2 7800 : 2 = 3900. Geht es weiter durch 2? Ja! 3900 : 2 = 1950. Geht es noch weiter? Ja! 1950:2=975. Weiter durch 2 geht es aber nicht.

Probieren wir dann durch 3. Geht es? Ja! 975:3=325. Geht es weiter durch 3? Nein! (325:3 = 108,33

Probieren wir die nächste Primzahl: 325:5=65. Das geht nochmal: 65:5=13.

Die nächsten Primzahlen sind 7 und 11, da geht es nicht. Es geht wieder durch 13 13:13=1.

Hier sind wir fertig. Wir haben 7800 drei mal durch 2, ein mal durch 3, zwei mal durch 5 und ein mal durch 13 dividiert und dann war das Ergebnis 1. Es gilt daher: 7800:2:2:2:3:5:5:13=1 und umgekehrt (Gegenrechnung) 7800=2·2·2·3·5·5·13.

Kürzen mit Primfaktorzerlegung

Wir haben schon das Kürzen von Brüchen gesehen:

${\frac {45}{35}}={\frac {45:5}{35:5}}={\frac {9}{7}}$

Hier sieht man sofort, dass man sowohl den Zähler als auch den Nenner durch 5 teilen kann. Was ist aber, wenn man große Zahlen hat? In diesem Fall ist es besser, die PFZ der Zahlen erst durchzuführen:

${\frac {6664}{8820}}=$?

6664	2
3332	2
1666	2
833	7
119	7
17	17
1

8820	2
4410	2
2205	3
735	3
245	5
49	7
7	7
1

Man schreibt Zähler und Nenner als Produkt von Primzahlen und kürzt den Bruch (also Primzahlen, die oben und unten vorkommen, werden gestrichen)

${\frac {6664}{8820}}={\frac {{\cancel {2}}\cdot {\cancel {2}}\cdot 2\cdot {\cancel {7}}\cdot {\cancel {7}}\cdot 17}{{\cancel {2}}\cdot {\cancel {2}}\cdot 3\cdot 3\cdot 5\cdot {\cancel {7}}\cdot {\cancel {7}}}}={\frac {2\cdot 17}{3\cdot 3\cdot 5}}={\frac {34}{45}}$

Arbeiten mit Termen

Term Definition

Ein Term ist ein mathematischer Ausdruck. $\textstyle {\color {Red}3+4}$,  $\textstyle {\color {Blue}s+x}$,  $\textstyle {\color {Red}t^{2}}$,  $\textstyle {\color {Cyan}r^{2}x-4r}$,  $\textstyle {\color {Red}{\frac {r^{2}x-4r}{w+9}}}$   sind alles Terme, wobei  $\textstyle {\color {Red}{\frac {r^{2}x-4r}{w+9}}}$   aus mehreren Teiltermen besteht.

Potenzen

Potenz Definition

Jeder Term der Form mⁿ ist eine Potenz. Was unten steht (hier m) nennt man Basis, was oben rechts (hier n) Hochzahl.

Potenz    $4_{\ \leftarrow {\text{Basis}}}^{3\ \ \leftarrow {\text{Hochzahl}}}$     Was bedeutet diese Schreibweise?

Wenn man 4+4+4 hat, kann man auch 3·4 schreiben: $\textstyle \underbrace {4+4+4} _{3\ mal}=3\cdot 4$. Eine Multiplikation zeigt, wie oft man eine Zahl mit sich selbst addiert.

Wenn man 4·4·4 hat, dann kann man 4³ schreiben. Eine Potenzzahl (hier 4³) zeigt, wie oft (so oft, wie die Hochzahl, hier 3) man eine Zahl (die Basis, hier 4) mit sich selbst multipliziert.

Potenzen Erklärung

Strichrechnungen unter Potenzzahlen

Wir haben gelernt, dass eine Multiplikation uns zeigt, wie oft die gleiche Zahl innerhalb einer Summe vorkommt. Beispielsweise ist $\textstyle \ \underbrace {4+4+4+4+4+4+4} _{{\color {red}7}\ mal}={\color {red}7}\cdot 4$. Das bedeutet allerdings auch, dass $\textstyle \ 2a+5a=7a\$ ist, weil $\textstyle \ 2a+5a=\underbrace {a+a} _{{\color {red}2}\ mal}+\underbrace {a+a+a+a+a} _{{\color {red}5}\ mal}=\underbrace {a+a+a+a+a+a+a} _{{\color {red}7}\ mal}=({\color {red}2+5})\cdot a={\color {red}7}a$

Eine Potenzzahl zeigt, wie oft die gleiche Zahl innerhalb eines Produktes vorkommt. Beispielsweise: $\textstyle \ \underbrace {5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5} _{{\color {red}6}\ mal}=5^{\color {red}6}$.

Was ist jetzt, wenn wir Potenzzahlen addieren (oder subtrahieren)?

Eine Vereinfachung einer Strichrechnung zwischen Potenzen ist nur dann möglich, wenn die Potenzzahl die gleiche Basis und die gleiche Hochzahl hat.

Nehmen wir ein Beispiel: $\textstyle \ 3a^{2}+5a^{4}-2a^{4}+7a^{2}-6b^{2}$.

Bei 3a² und 7a² hat die Potenzzahl a² die gleiche Basis a und die gleiche Hochzahl 2. Diese Potenzen können zusammengerechnet werden:

$\textstyle \ 3a^{2}+7a^{2}=10a^{2}$

Entsprechend können wir mit a⁴ arbeiten:

$\textstyle \ 5a^{4}-2a^{4}=3a^{4}$

a² und a⁴ können wir hingegen nicht zusammenrechnen, da sie zwar die gleiche Basis a aber nicht die gleiche Hochzahl (2 bzw. 4) haben.

a² und b² können wir auch nicht zusammenrechnen, da sie zwar die gleiche Hochzahl 2 aber nicht die gleiche Basis (a bzw. b) haben.

Daher ist: $\textstyle \ 3a^{2}+5a^{4}-2a^{4}+7a^{2}-6b^{2}=10a^{2}+3a^{4}-6b^{2}$

Warum ist es so? Wie schon erwähnt, können nur gleiche Summanden durch eine Multiplikation ersetzt werden:

$\textstyle \ \underbrace {3+3+3+3+3+3+3} _{{\color {red}7}\ mal}={\color {red}7}\cdot 3$

Wenn wir 3⁴ und 3² anstatt 3 haben, sind die Summanden nicht gleich, da 3⁴=3·3·3·3=81 und 3²=3·3=9 ist:

$\textstyle \ {3^{4}+3^{2}+3^{4}+3^{4}+3^{2}+3^{4}+3^{4}}\neq {\color {red}7}\cdot 3$

$\textstyle \ {3^{4}+3^{2}+3^{4}+3^{4}+3^{2}+3^{4}+3^{4}}=81+9+81+81+9+81+81=\dots$

$\textstyle \ \dots =\underbrace {81+81+81+81+81} _{{\color {red}5}\ mal}+\underbrace {9+9} _{{\color {red}2}\ mal}={\color {red}5}\cdot 81+{\color {red}2}\cdot 9={\color {red}5}\cdot 3^{4}+{\color {red}2}\cdot 3^{2}(=423)$

Nur Potenzen, die sowohl die gleiche Basis als auch die gleiche Hochzahl haben, können zusammengerechnet werden.

Noch ein Beispiel: $\textstyle \ 11w^{3}+5c^{3}-7w^{3}+8c^{5}-12c^{3}+2w^{3}-3c^{5}=6w^{3}-7c^{3}+5c^{5}$

 

Multiplikation von zwei Potenzen mit der gleichen Basis

Zwei Potenzzahlen mit der gleichen Basis kann man multiplizieren, indem man die gleiche Basis und als Hochzahl die Summe der Hochzahlen schreibt.

$4^{3}\cdot 4^{6}=4^{3+6}=4^{9}\quad \quad a^{t}\cdot a^{q}=a^{t+q}\quad \quad x^{3}\cdot x^{57}=x^{3+57}=x^{60}$

Warum das so ist, ist leicht zu erklären:

$4^{3}\cdot 4^{6}=\underbrace {4\cdot 4\cdot 4} _{3\ mal}\cdot \underbrace {4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4} _{6\ mal}=\underbrace {4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4} _{9\ mal}=4^{9}\quad _{(=4^{3+6})}$

Die Hochzahlen addiert man, auch wenn sie negativ sind:

$4^{7}\cdot 4^{-2}=4^{7+(-2)}=4^{5}\quad \quad a^{t}\cdot a^{-q}=a^{t+(-q)}=a^{t-q}\quad \quad x^{3}\cdot x^{-7}=x^{3+(-7)}=x^{3-7}=x^{-4}$

Allgemein kann man daher folgern:

$a^{n}\cdot a^{m}=a^{n+m}$

wobei n und m irgendwelche positive oder negative reelle Zahlen sein können. Für den Fall von natürlichen Hochzahlen können wir schreiben:

$a^{n}\cdot a^{m}=\underbrace {a\cdot a\cdot \dots \ \cdot a} _{n\ mal}\cdot \underbrace {a\cdot a\cdot \dots \ \cdot a} _{m\ mal}=\underbrace {a\cdot a\cdot \dots \ \cdot a} _{n+m\ mal}=a^{n+m}$

Vorischt! Bei einer Addition oder Subtraktion von Potenzen kann man dagegen die Hochzahlen nicht addieren!

$4^{3}+4^{6}\neq 4^{9}$

Klammer Auflösen

Ziel des Ausmultiplizierens

Lösen Sie die Klammern auf!

$2(3x-5)\qquad (1)$

Ziel solcher Aufgaben ist, einen Ausdruck ohne Klammern zu schreiben, der gleichwertig zu diesem Ausdruck (mit Klammern) ist. Probieren wir zunächst einmal die Klammern einfach wegzulassen. Zuerst soll man etwas erklären:

Wenn zwischen zwei mathematischen Ausdrücken nichts (keine Rechenart) steht, ist ein "mal" gemeint (Multiplikation) (einzige Ausnahme sind hier die gemischten Zahlen)

${\begin{matrix}2(3x-5)=\\6x-5\end{matrix}}\qquad (2)$

Probieren wir jetzt in beiden Ausdrücken eine Zahl an der Stelle von x einzusetzen, beispielsweise 0:

$(1)\quad \rightarrow \quad 2(3{\cancel {x}}^{=0}-5)=-10$ $(2)\quad \rightarrow \quad 6{\cancel {x}}^{=0}-5=-5$

Die beide Ausdrücke sind nicht gleich. Probieren wir es auch mit 1:

$(1)\quad \rightarrow \quad 2(3{\cancel {x}}^{=1}-5)=-4$ $(2)\quad \rightarrow \quad 6{\cancel {x}}^{=1}-5=1$

Wieder sind die Ausdrücke nicht gleich. Man sagt dann, dass  $2(3x-5)\neq 6x-5$  ist, dass  $2(3x-5)$  nicht gleich zu  $6x-5$  ist. Obwohl eine Zahl schon ausreichen könnte, stimmt das eigentlich für alle Zahlen, die man für $x$ einsetzen kann.

Probieren wir dann beide Summanden in der Klammer mit dem Ausdruck außerhalb der Klammer zu multiplizieren:

${\begin{matrix}2(3x-5)=\\6x-10\end{matrix}}\qquad (3)$

Egal mit welcher Zahl wir es jetzt ausprobieren, werden die beide Ausdrücke immer gleich sein! Beispielsweise mit $4$:

$(1)\quad \rightarrow \quad 2(3{\cancel {x}}^{=4}-5)=14$ $(3)\quad \rightarrow \quad 6{\cancel {x}}^{=4}-10=14$

Da das immer gilt, kann man schreiben:

$2(3x-5)=6x-10$

Wir haben daher unser Ziel erreicht! Wir haben einen gleichwertigen Ausdruck ohne Klammern!

Klammern werden aufgelöst, indem jeder Summand in Klammern mit dem Ausdruck außerhalb der Klammer multipliziert wird.

Erklärung des Ausmultiplizierens

Denken wir an eine Kiste die 2 Zitronen und 4 Birnen hat:

Nehmen wir an, dass wir diese Kiste 3 mal haben:

In diesem Fall haben wir 3 mal 2 also 6 Zitronen und 3 mal 4 also 12 Birnen.

Den Inhalt der Kiste müssen wir mit 3 multiplizieren und zwar muss jede verschiedene Sorte, die in der Kiste ist, mit 3 multipliziert werden.

Ein Klammer ist genau so wie eine Kiste:

$3\cdot (2z+4b)=3\cdot 2z+3\cdot 4b=6z+12b$

Wir haben einfach statt Bilder für die Zitronen den Buchstabe z und für die Birnen den Buchstabe b benutzt.

Es spielt keine Rolle, ob außerhalb der Kiste eine Zahl oder ein Symbol steht:

$a\cdot (2z+4b)=a\cdot 2z+a\cdot 4b=2a\ z+4a\ b$

Zwischen 2z und 4b steht ein Plus. Der Vorgang ist der gleiche bei Minus:

$a\cdot (2z-4b)=a\cdot 2z-a\cdot 4b=2a\ z-4a\ b$

Auch wenn wir Minus haben, können wir die verschiedenen Sorten (hier 2z und 4b) Summanden nennen.

Ein Klammer wird ausmultipliziert, indem jeder Summand in der Klammer mit der Sache außerhalb der Klammer multipliziert wird.

Beispiel: $\ 5a\cdot (2z-4b+3c)=5a\cdot 2z-5a\cdot 4b+5a\cdot 3c=10a\ z-20a\ b+15a\ c$

Ausmultiplizieren mit einer oder zwei Klammer ==== ===== Aufgaben mit einer Klammer =

Lösen Sie die Klammern auf!

$2x^{2}(3x^{5}-7+5x)$

Die Aufgabe hier ist, einen gleichwertigen Ausdruck ohne Klammern zu schreiben. Wie eben erklärt, multipliziert man dafür den Term außerhalb der Klammer ( $2x^{2}$ ) mit jedem Summand in den Klammern (also erst mit  $3x^{5}$ , dann mit  $7$  und dann mit  $5x$ ):

Der Ausdruck am Ende ist immer gleich mit dem Ausdruck am Anfang. Wir haben also die Klammer aufgelöst!

Aufgaben mit 2 Klammern

Lösen Sie die Klammern auf!

$(2x^{2}-5)(3x^{2}-4)$

Die Aufgabe hier ist wieder, einen gleichwertigen Ausdruck ohne Klammern zu schreiben. Um das zu machen, multipliziert man jeden Summand der ersten Klammer  $(2x^{2}-5)$  mit jedem Summand der zweiten Klammer  $(3x^{2}-4)$ :

Zu bemerken ist, dass −8x²−15x² eine Strichrechnung zwischen Potenzen ist. Daher gelten hier die entsprechenden Regel der Strichrechnungen unter Potenzzahlen

Hier gilt die Multiplikationsregel der Vorzeichen: plus mal plus ist plus, plus mal minus ist minus, minus mal plus ist minus, minus mal minus ist plus. (Das Gleiche gilt bei durch)

+ · + = +

+ · − = −

− · + = −

− · − = +

Hier ist darauf zu achten, dass die Regel ausschließlich bei Punktrechnungen gilt (Multiplikation und Division). Hier ein paar Beispiele, die den Zusammenhang klar machen sollten:

5−6=−1
In diesem Fall haben wir eine Strichrechnung zwischen zwei Zahlen: 5 MINUS 6, was insgesamt MINUS 1 beträgt.

5·(−6)=−30
In diesem Fall haben wir eine Punktrechnung (mal) zwischen eine positive und eine negative Zahl, also hier gilt + · − = − und die Werte 5 und 6 müssen wir multiplizieren (5 mal 6 ist 30).

−20−4=−24
In diesem Fall haben wir eine Strichrechnung zwischen zwei Zahlen, wobei die erste Zahl negativ ist, also MINUS 20 MINUS 4, was insgesamt MINUS 24 beträgt.

−20 : (−4)=5
In diesem Fall haben wir eine Punktrechnung (durch) zwischen zwei negative Zahlen, also hier gilt − · − = + und die Werte 20 und 4 müssen wir dividieren (20 durch 4 ist 5).

5+6=11
In diesem Fall haben wir eine Strichrechnung zwischen zwei Zahlen: 5 PLUS 6, was insgesamt 11 beträgt.

5·6=30
In diesem Fall haben wir eine Punktrechnung (mal) zwischen zwei positive Zahlen, also hier gilt + · + = + und die Werte 5 und 6 müssen wir multiplizieren (5 mal 6 ist 30). Diese Berechnung ist gleichbedeutend mit (+5)·(+6)=30.

Die Berechnung 5−6=−1 ist gleichbedeutend mit 5+(−6)=−1. Hier haben wir zwar keine ausdrückliche Multiplikation, wir addieren allerdings eine negative Zahl. In solchen Fällen sollen wir schon die plus mal minus Regel anwenden, wir haben aber doch keine Multiplikation, also 5 wird NICHT mit 6 multipliziert. Die Regel gilt nur für die Vorzeichen. Daher gilt:
5+(+6)=11
5−(+6)=−1
5−(−6)=5+6=11
5+(−6)=−1
Es gilt auch: −5+6=1

Umformen

Umformen Grundwissen Gegenrechnungen

Nachdem Vassili Lisa drei Äpfel gibt, hat er fünf Äpfel. Wie viele Äpfel hatte er vorher?

Wie kann man diese Aufgabe in der mathematischen Sprache schreiben? Für das Gefragte (wie viele Äpfel) wird in Mathematik irgendein Symbol benutzt, als Stellvertreter für die noch unbekannte Zahl. In der Regel wird als Symbol ein Buchstabe verwendet und nicht allzu selten x.
Mit x sind also die Äpfel gemeint, die Vassili am Anfang hatte. Wir wissen noch nicht, wie viele sie waren, daher schreiben wir ein Symbol dafür, ein Buchstabe, also x.

Wenn Vassili drei Äpfel der Lisa gibt, dann hat er weniger Äpfel als zuvor, es geht um eine Subtraktion. Von den x Äpfeln am Anfang sind drei Äpfel zu subtrahieren. Dass dann noch fünf Äpfel bleiben, wird durch den folgenden mathematischen Ausdruck geschrieben:

x−3=5

Man kann für x verschiedene Zahlen ausprobieren, z.B. 2, 3, 7, 8 oder 9. So kann man schon feststellen, dass nur acht minus drei gleich fünf ist. „x“ muss also 8 sein, damit die Rechnung stimmt. Vassili hatte also 8 Äpfel am Anfang.

Die ganze Zeit ausprobieren ist allerdings nicht gerade geschickt. Besonders bei größeren Zahlen wird es sogar ziemlich schwer. Es gibt in der Mathematik einen geschickteren Weg, die Aufgabe zu lösen. Man benutzt die sogenannte Gegenrechnung. Bei allen Gleichungen gibt es zwei Teile, ein Teil links vom „=“ und ein Teil rechts vom „=“. Bringt man einen Term von einer Seite zur anderen, dann muss man die Gegenrechnung benutzen.

Die Gegenrechnung der Subtraktion ist die Addition und umgekehrt.

Wenn x−3=5 ist, dann kann man die 3 auf die andere Seite vom „=“ bringen und statt minus die Gegenrechnung (plus) benutzen:

x=5+3       also x=8

Bei der Aufgabe c+4452 = 341 bringt man 4452 auf die andere Seite und benutzt die Gegenrechnung von minus. Die Lösung ist daher:

c+4452 = 341 → c= 341−4452 → c = −4111

Die Gegenrechnung der Multiplikation ist die Division und umgekehrt.

3f=114

Zwischen 3 und f steht nichts.

Wenn in Mathematik zwischen zwei Ausdrucken (zum Beispiel einer Zahl und einem Symbol, einer Klammer und einer Zahl und so weiter) nichts steht, dann ist Multiplikation gemeint (einzige Ausnahme: die gemischten Zahlen).

Da zwischen 3 und f nichts steht, ist mal gemeint. f ist ein Symbol und steht für irgendeine Zahl. Die Aufgabe ist herauszufinden, wie viel f sein soll, damit die Rechnung stimmt. In diesem fall soll 3 auf die andere Seite gebracht und die Gegenrechnung von mal (also durch) benutzt werden:

3f=114 (nichts zwischen 3 und f, also mal gemeint):

3·f=114 (3 auf die andere Seite von „=“ bringen und Gegenrechnung, also hier Division, benutzen)

f=114:3 und daher

f = 38.

Man kann auch einen Bruch statt einer Division benutzen:

$f={\frac {114}{3}}=38$

Entsprechend ist die Gegenrechnung der Division die Multiplikation:

$\textstyle {\frac {k}{5}}=11$    also k:5 = 11 und daher k = 11 · 5

k = 55

Was ist aber die Gegenrechnung vom Quadrat?

Die Gegenrechnung von Quadrat ist die sogenannte „Wurzel“:

z² = 81 also z = ${\sqrt {81}}$  und daher z=9

9 ist die Zahl, deren Quadrat 81 ist, daher ist die Wurzel von 81 gleich 9. Wenn wir in der Gleichung z² = 81 z durch 9 ersetzen, dann stimmt die Gleichung tatsächlich: 9² = 81

Selbstverständlich ist die Gegenrechnung der Wurzel das Quadrat.

${\sqrt {m}}$ = 13 also m = 13² und daher m=169

Obwohl es für das Niveau dieses Buches nicht absolut notwendig ist, können wir doch auf eine Tatsache aufmerksam machen: Die Gleichung z² = 81 hat noch eine Lösung, wenn z gleich −9 ist. Freilich stimmt die Gleichung (−9)² = 81. (−9)² bedeutet (−9)·(−9). Minus mal minus ist plus und daher:

(−9)² =(−9)·(−9)= + 9·9 = 81 also

(−9)² = 81

Umformen einfache Kombinationen

Wenn man mehrere Summanden und Rechenarten und eine unbekannte Variable hat, dann soll man alle Teilterme (Summanden) mit der gesuchten Variable auf eine Seite bringen. Im Folgenden werden alle Terme mit der gesuchten Variable nach links gebracht. Die restlichen Terme werden auf die andere Seite gebracht (das geht aber selbstverständlich auch umgekehrt). Schauen wir ein Beispiel an:

5x − 7 = 3x + 11

Wir wählen die linke Seite als die Seite, in der die Teilterme (Summanden) mit der gesuchten Variable (x) sein werden. Wir haben zwei solchen Teilterme, 5x und 3x. 5x ist schon auf der linken Seite, wir müssen also noch 3x auf die andere Seite bringen. Vor 3x steht das Symbol „=“. Ist 3x jetzt positiv oder negativ? Wenn man b=4 schreibt, ist +4 oder −4 gemeint? Die Antwort ist +4. Daher auch hier, wenn nach dem Symbol „=“ kein plus oder minus steht, dann ist ein plus gemeint. Wenn man 5x − 7 = 3x + 11 schreibt, ist es das Gleiche wie + 5x − 7 = + 3x + 11. Wenn man den Term 3x auf die andere Seite bringt, muss man die Gegenrechnung benutzen, also Subtraktion (minus).

5x − 7 − 3x = 11

7 hat kein x neben sich, sie muss auch auf die rechte Seite gebracht werden, wieder mit der Gegenrechnung, also diesmal mit Addition (plus):

5x − 3x = 11 + 7

Das Ganze kann man in einem Schritt machen:

5x − 7 = 3x + 11

5x − 3x = 11 +7

2x = 18
(Hier haben wir einfach die Rechnungen gemacht: 5x-3x ist 2x und 11+7 ist 18).

Es bleibt noch, 2 auf die andere Seite zu bringen. Zwischen 2 und x steht nichts, daher ist eine Multiplikation gemeint. Die Gegenrechnung ist eine Division:

x = $\textstyle {\frac {18}{2}}$ und daher x = 9

Man kann das ganze auch so erklären:

5x − 7 = 3x + 11

Man will, dass auf der rechten Seite 3x verschwindet. Das kann passieren, indem man 3x subtrahiert. Ein Gleichung aber ist wie eine Waage. Das Gleichungssymbol (=) teilt die Gleichung in zwei Teilen, links und rechts. Was auf der einen Seite passiert, muss auch auf der anderen stattfinden, damit das Gleichgewicht erhalten bleibt. Man benutzt folgende Schreibweise:

5x − 7 = 3x + 11      | −3x (Man schreibt am Rand, was auf beiden Seiten zu tun ist)

5x − 7 − 3x = 3x + 11 − 3x

2x − 7 = 11

Man will aber auf der linken Seite nur Teilterme (Summanden) mit x haben, deshalb muss die -7 dort verschwinden. Das geht, indem man 7 auf beiden Seiten addiert.

2x − 7 = 11      | +7

2x − 7 + 7 = 11 + 7

2x = 18

Jetzt bleibt nur die Division:

2x = 18      | :2

x = 18 : 2      (Man kann auch  $\textstyle x={\frac {18}{2}}$  schreiben)

x = 9

Sofern mehrere Teilrechnungen oder Zwischenschritte im Kopf durchgeführt werden, wird zusammengefasst und kürzer notiert:

5x − 7 = 3x + 11      | −3x+7

2x = 18      | :2

x =  $\textstyle {\frac {18}{2}}$

x = 9

Wenn die Variable innerhalb einer Klammer steht, ist der erste Schritt, die Klammer aufzulösen, sonst geht man wie vorher vor:

4y + 3 (7 − 5y) = 11 − 6y

4y + 21 − 15y = 11 − 6y | −21

4y − 15y = 11 − 6y −21 | +6y

4y − 15y + 6y = 11 − 21

− 5y = −10 | : (−5)

y=2

Wenn man y durch 2 in der Anfangsgleichung 4y + 3 (7 − 5y) = 11 − 6y ersetzt, stellt man fest, dass die Gleichung tatsächlich stimmt.

4y + 3 (7 − 5y) = 11 − 6y

4·2 + 3 (7 − 5·2) = 11 − 6·2

8 + 3 ·(−3) = 11 − 12

8 − 9 = − 1

In der Tat ist 2 der einziger Wert von y, für den die Gleichung wirklich stimmt. Die LeserInnen können andere Werte ausprobieren und feststellen, dass die Gleichung dann nicht mehr stimmt.

Schluss und Prozentrechnung

Schlussrechnung (Dreisatz)

Direkte Proportionalität

Fangen wir direkt mit einem Beispiel an.

• 5 Tische kosten 315€. Wie viel kosten 2 Tische?

Hier spricht man von einer sogenannten direkte Proportionalität. Weniger Tische werden weniger Geld kosten. Das Beispiel besteht aus zwei Sätze:

was gegeben ist: „5 Tische kosten 315€“. Diese Daten schreibt man auf ein Zeile nebeneinander. Man schreibt also am Anfang:

5 Tische ... 315€

was gefragt ist: „Wie viel kosten 2 Tische?“ Hier ist der Preis der Tische in € gefragt. Man schreibt eine zweite Zeile unter die erste: Dabei schreiben wir das Gefragte (Preis der Tische) als x und die Anzahl der Tische unter der Anzahl Tische von der ersten Zeile:

5 Tische ... 315€

2 Tische ... x

Man fängt mit der gefragten Größe an (hier €), also mit der Zahl, die an der gleichen
Spalte mit x steht, und multipliziert diese Zahl mit der Zahl schräg gegenüber.

315·2=630.

Das Ergebnis dividiert man mit der verbliebenden Zahl (hier 5).

630:5=126

Jetzt kommt die Frage: 126 was? Was haben wir hier gerechnet? Sicherlich nicht Frösche und auch nicht Äpfel. Wie kann man herausfinden, was hier gerechnet wurde? Eine Möglichkeit ist es, die folgende Frage zu stellen: „Wieviel kosten 2 Tische?“ Kosten sind gefragt, also €. Das Ergebnis ist daher der Wert in €. Ein anderer Weg ist es darauf zu schauen, wo x steht: Es steht unterhalb von „315€“. Wir haben gesagt, dass in jeder Spalte die Sachen (in Mathematik „Einheiten“ genannt) übereinstimmen müssen. Unterhalb von € müssen € stehen. Daher sollte die Einheit von x auch € sein. Somit ist die Antwort:

„Zwei Tische kosten 126€.“

Der ganze Prozess noch einmal Schritt für Schritt:

Noch ein Beispiel:

3,5 Liter eines Stoffes wiegen 14,7 kg.

a) Wie viel wiegen 0,0175 Liter?

b) Wie viel Liter sind 3850kg?

Hier gibt es zwei Fragen, das gegebene ist aber in beiden Fällen das gleiche, nämlich der erste Satz.

a) Für die erste Frage schreiben wir das gegebene an einer Zeile und das gefragte darunter (gleiche Sachen unter gleichem):

${\begin{matrix}{\text{3,5 Liter}}\\\uparrow :\\{\text{0,0175 Liter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$

Die Zahl, die an der gleichen Spalte mit x steht, mal die Zahl schräg gegenüber und durch die andere Zahl:

$\left({\frac {14{,}7\cdot 0{,}0175}{3{,}5}}\right)\qquad x=0{,}735\ \ kg$

Noch einmal stellt sich die Frage: 0,735 was? Was haben wir hier gerechnet? Wieso haben wir kg geschrieben? Die Frage war „Wie viel wiegen 0,0175 Liter?“ Also muss die Einheit vom Ergebnis kg sein. Wenn wir die Schlussrechnung betrachten, sehen wir ebenfalls, dass x unterhalb von „14,7 kg“ steht. In einer Spalte müssen die Einheiten übereinstimmen, unterhalb von kg müssen gleichfalls kg stehen. Somit ist die Antwort:

„0,0175 Liter des Stoffes wiegen 0,735kg.“

b) Für die zweite Frage schreiben wir wieder das gegebene in einer Zeile und das gefragte darunter (gleiche Sachen (Einheiten) unter gleiche):

${\begin{matrix}{\text{3,5 Liter}}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\:\uparrow \\{\text{3850 kg}}\end{matrix}}$     $\left({\frac {3{,}5\cdot 3850}{14{,}7}}\right)\qquad x\approx 916{,}7\ {\text{ Liter}}$

Ob man die Liter links oder rechts schreibt oder das gegebene oben oder unten, spielt keiner Rolle. Wichtig ist: das Gegebene in einer Zeil und gleiche Sachen (Einheiten) in der gleichen Spalte!

${\begin{matrix}{\text{14,7 kg}}\\\uparrow :\\{\text{3850 kg}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{3,5 Liter}}\\{}\\x\end{matrix}}$     $\left({\frac {3{,}5\cdot 3850}{14{,}7}}\right)\qquad x\approx 916{,}7\ {\text{Liter}}$

In diesen Aufgaben ist es wichtig zu verstehen: Man braucht nicht wissen, was die Wörter bedeuten! Man soll einfach die Struktur der Sätze der Aufgabe verstehen!

Indirekte Proportionalität

In der direkten Proportionalität haben wir gesehen, wie man vorgeht, wenn zwei Größen gleichzeitig größer oder kleiner werden. Wenn man mehr von einer Ware kaufen will, dann muss man auch mehr bezahlen. Wenn man weniger kaufen will, dann zahlt man auch weniger. Wenn man mehr kg von einem Stoff hat, dann hat man auch mehr Liter des Stoffes. Es gibt aber auch Fälle, bei denen die Erhöhung einer Größe die Verminderung einer anderen bedeutet:

• 3 Arbeiter brauchen 15 Stunden, um ein Haus mit Fliesen zu verlegen. Wie viel Zeit brauchen dann 5 Arbeiter?

1 Arbeiter würde in diesem Fall mehr Zeit brauchen. Es gibt für einen Arbeiter viel mehr Boden zu verlegen, wenn er alleine arbeitet. Also weniger Arbeiter brauchen mehr Zeit. Das ist also KEINE direkte sondern eine indirekte Proportionalität.

Wie bei der direkten Proportionalität schreibt man hier auch die gegebenen Größen nebeneinander und gleiche Größen untereinander.

${\begin{matrix}{\text{3 Arbeiter}}\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\x\end{matrix}}$

In diesem Fall multipliziert man mit der Zahl gerade gegenüber (und NICHT schräg gegenüber, wie in der direkten Proportionalität) und dividiert dann durch die andere Zahl:

${\begin{matrix}{\text{3 Arbeiter}}\\\downarrow :\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}{\dot {\longleftarrow }}\\\\{}\end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$      $\left({\frac {15\cdot 3}{5}}\right)\qquad x=9\ {\text{Stunden}}\ \$  (die die Arbeiter in diesem Fall brauchen).

Um zu unterscheiden, ob man eine direkte oder indirekte Proportionalität hat, muss man schon die Sprache und die Zusammenhänge gut verstehen können!

Vergleich direkter und indirekter Proportionalität

Wie wir in den vorherigen Absätzen gesehen haben, muss man sowohl bei der direkten als auch bei der indirekten Proportionalität die Daten, die (in der Regel in einem Satz) in Verbindung gebracht werden, in einer Zeile nebeneinander schreiben (hier bei der direkten Proportionalität 3,5 Liter und 14,7 kg und bei der indirekten 3 Arbeiter und 15 Stunden) und dafür sorgen, dass in jeder Spalte die gleichen Einheiten geschrieben werden.

${\begin{matrix}{\text{3,5 Liter}}\\\\{\text{0,0175 Lit}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\{}\\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$

${\begin{matrix}{\text{3 Arbeiter}}\\{}\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$

Bei beiden Vorgängen fängt man dann mit der Zahl an, die nur an der gleichen Spalte mit x steht (hier 14,7 kg in der direkten und 15 Stunden in der indirekten Proporionalität). Der Unterschied ist: bei der direkten Proportionalität geht man dann schräg, bei der indirekten gerade gegenüber, und multiplitiert mit dieser Zahl (hier 0,0175 Liter in der direkten und 3 Arbeiter in der indirekten Proporionalität). Am Ende dividiert man in beiden Fällen mit der übriggebliebenen Zahl (hier 3,5 Liter in der direkten und 5 Arbeiter in der indirekten Proporionalität).

${\begin{matrix}{\text{3,5 Liter}}\\\uparrow :\\{\text{0,0175 Lit}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$

${\begin{matrix}{\text{3 Arbeiter}}\\\downarrow :\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}{\dot {\longleftarrow }}\\\\{}\end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$

Wie kann man verstehen, ob eine direkte oder eine indirekte Proportionalität vorliegt?

Nehmen wir den folgenden Bruch b:  $\textstyle b={\frac {z}{n}}$,  wobei z der Zähler und n der Nenner ist. Wenn z=20 und n=5 ist, dann ist der Bruch b=4: $\textstyle b={\frac {20}{5}}=4$. Wenn jetzt der Zähler z größer wird (z.B. z=30), dann wird der ganze Bruch b auch größer:  $\textstyle b={\frac {30}{5}}=6$. Wenn der Zählerz kleiner wird (z.B. z=10), dann wird der ganze Bruch auch kleiner:  $\textstyle b={\frac {10}{5}}=2$. Je größer der Zähler, desto größer der Bruch. Je kleiner der Zähler, desto kleiner der Bruch. Diesen Zusammenhang nennt man direkte Proportionalität.

Wenn jetzt der Nenner größer wird (z.B. n=10), dann wird der ganze Bruch das Gegenteil, also kleiner:

Wenn der Zähler z=20 und der Nenner n=5 ist, dann ist der Bruch b=4: $\textstyle b={\frac {20}{5}}=4$. Wird der Nenner n größer, z.B. 10, dann wird der Bruch b kleiner:  $\textstyle b={\frac {20}{10}}=2$. Wenn der Nenner kleiner wird (z.B. n=2), dann wird der ganze Bruch das Gegenteil, also größer:  $\textstyle b={\frac {20}{2}}=10$. Je größer der Nenner, desto kleiner der Bruch. Je kleiner der Nenner, desto größer der Bruch. Diesen Zusammenhang nennt man indirekte Proportionalität.

Wenn zwei Größen (z.B. Volumen und grob gesagt Gewicht) gleichzeitig wachsen oder gleichzeitig weniger werden, dann liegt eine direkte Proportionalität vor (z.B. wenn man mehr Wasser hat, ist sowohl das Volumen als auch das Gewicht mehr). Wenn das Wachstum einer Größe zur Verminderung einer anderen führt, dann liegt eine indirekte Proportionalität vor (z.B. mehr Arbeiter brauchen weniger Zeit, um die gleiche Arbeit zu erledigen). So kann man verstehen, ob man direkte oder indirekte Proportionalität benutzen soll. Beim nächsten Kapitel allerdings (Prozentrechnung) kommt nur die direkte Proportionalität vor!

Prozentrechnung

Prozentrechnung allgemein

Prozentrechung Begriffe

Grundaufgaben der Prozentrechnung

Nicht vergessen: Der Wert am Anfang (das „Ganze“) ist immer 100%

• Wie viel % von 55 Personen sind 11 Personen?

Der Wert am Anfang (das „Ganze“) ist immer 100%. Hier ist der Prozentsatz eines Teils von 55 Personen gefragt. 55 Personen sind 100%. (Nach dem Wort „von“ steht der Wert, der 100% ist). Wir schreiben das so auf, wie wir es in der Schlussrechnung (genauer in der direkten Proportionalität) gelernt haben:

${\begin{matrix}{\text{55 Personen }}\\\uparrow :\\{\text{11 Personen }}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\{}\\x\end{matrix}}$      $\left({\frac {100\cdot 11}{55}}\right)\qquad x=20\%$.

• Wie viele Personen sind 11% von 55 Personen?

Der Wert am Anfang (das „Ganze“) ist immer 100%. Hier ist ein Prozentsatz von 55 Personen gefragt, also haben wir am Anfang 55 Personen, die dann 100% sind! (Also nach dem Wort „von“ steht der Wert, der 100% ist). Wir schreiben das auf, wie wir es in der Schlussrechnung (genauer in der direkten Proportionalität) gelernt haben:

${\begin{matrix}{\text{55 Personen }}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\:\uparrow \\11\%\end{matrix}}$      $\left({\frac {55\cdot 11}{100}}=6{,}05\right)\qquad x\approx 6\ {\text{Personen}}$.

• Wie viel % von 23 kg sind 5329kg?

Hier steht nach „von“ 23 kg, also sind 23kg 100%

${\begin{matrix}{\text{23 kg}}\\\uparrow :\\{\text{5329 kg}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\{}\\x\end{matrix}}$      $\left({\frac {100\cdot 5329}{23}}\right)\qquad x\approx 23170\%$.

• Wie viel ist 0,3% von 0,26 Liter?

${\begin{matrix}{\text{0,26 Liter}}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\:\uparrow \\0{,}3\%\end{matrix}}$      $\left({\frac {0{,}26\cdot 0{,}3}{100}}\right)\qquad x=0{,}00078\ {\text{Liter}}$.

• Von wie vielen Personen sind 55 Personen 11%?

Hier steht nach dem Wort „von“ eine Frage. Das Gefragte schreibt man in der Mathematik mit x. Daher ist x 100%. Das Gefragte ist 100%.

${\begin{matrix}x\\{}\\{\text{55 Personen }}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\nearrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\:\downarrow \\11\%\end{matrix}}$      $\left({\frac {55\cdot 100}{11}}\right)\qquad x=500\ {\text{Personen}}$.

Prozentrechnung bei Wachstum oder Zerfall

Umkehraufgaben der Prozentrechnung

• Man hat in seinem Haus ein neues Zimmer aufgebaut. Die Fläche des Hauses ist dadurch um 15% auf 112,7m² gewachsen. Berechnen Sie die ursprüngliche Fläche!

Der Wert am Anfang (das „Ganze“) ist immer 100%. Hier wissen wir nicht, wie groß das Haus am Anfang war, das ist doch gefragt! Das gefragte schreibt man in Mathematik mit x. 100% ist also x. Das Haus ist um 15% gewachsen, also die Fläche am Ende (112,7m²) ist 100%+15%=115%. Daher sind 112,7m² 115%.

Schreiben wir diese Information auf, wie wir das gelernt haben:

${\begin{matrix}100\%\\\downarrow :\\115\%\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\nwarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}x\\{}\\{\text{112,7 m}}^{2}\end{matrix}}$      $\left({\frac {112{,}7\cdot 100}{115}}\right)\qquad x=98\ \mathrm {m} ^{2}$.

• Ein Tisch wurde um 10% geschnitten. Die neue Länge ist 2,7m. Berechnen Sie die ursprüngliche Länge!

Der Wert am Anfang (das „Ganze“) ist immer 100%. Er ist aber nicht gegeben. Daher ist x 100%. Der Tisch wurde um 10% geschnitten, war am Anfang 100%, daher bleibt noch 100%-10%=90%. 2,7m (der Wert am Ende) sind daher 90%. Schreiben wir das Ganze auf:

${\begin{matrix}100\%\\\downarrow :\\90\%\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\nwarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}x\\{}\\{\text{2,7 m}}\end{matrix}}$      $x=3\ \mathrm {m}$.

Erklärung der Prozent und Schlussrechnung

Wie schon betont, bedeutet "ein Prozent" das gleiche wie ein Hundertstel. Ein Hundertstel ist ein Bruch.Für die Erklärung der Prozentrechnung kann man daher die Bruchrechnung benutzen, genauer gesagt das Erweitern von Brüchen.

Wenn wir wissen wollen, wie viel Prozent von 5kg 3kg sind, können wir mit der Darstellung von 5kg anfangen:

Drei kg kann man dann als Bruchteil von diesen 5kg darstellen, wie im folgenden Bild:

Wenn jemand das Ganze senkrecht auf 20 teilt, ist jeder kleiner Teil ein Hundertstel. Im Bild kann man schon sehen, dass die drei fünftel $3\cdot 20=60$ solche kleine Teile sind, also 60 Hundertstel, also 60%:

Wenn wir jetzt mit Brüchen arbeiten, können wir durch die Bilder leicht verstehen, dass wir den Bruch $\textstyle 3 \over 5$ mit der Zahl 20 erweitert haben:

${3 \over 5}={\frac {3\cdot 20}{5\cdot 20}}={60 \over 100}=60\%$

Wie sind wir auf die Zahl 20 gekommen? Wir haben einfach 100 durch 5 dividiert, also durch die Zahl, die den Wert des Ganzen darstellt. Wieso ist 5 das Ganze? Wir haben schon in den Definitionen gesagt, dass das Ganze nach dem Wort "von" steht, also hier die 5 kg. So wie wir die Prozentrechnung gelernt haben, bedeutet das, dass man mit der Zahl quer gegenüber multiplizieren muss und durch die andere Zahl dividieren:

${\begin{matrix}{\text{5 kg}}\\\uparrow :\\{\text{3 kg}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\{}\\x\end{matrix}}$         $\left(100\cdot {3 \over 5}=3\cdot {100 \over 5}=3\cdot 20=60\right)\qquad x=60\%$

3 kg sind daher 60% (also 60 Hundertstel) von 5 kg.

Schauen wir jetzt ein Beispiel mit Zahlen, die nicht so "rund" sind:

Wie viel Prozent von 17 Äpfel sind 230 Äpfel?

Hier ist das Ganze die 17 Äpfel, also was nach dem Wort "von" (also in Genitiv) steht. Welcher Anteil von 17 Äpfel sind 230 Äpfel?

${230 \over 17}$

Diesen Bruch müssen wir so erweitern, damit im Nenner am Ende 100 steht:

${230 \over 17}={\frac {230\cdot 100:17}{17\cdot 100:17}}$

Der Nenner hier wird tatsächlich 100 sein (es gilt: ${17\cdot 100:17}=1700:17=100$). Somit haben wir:

${\frac {230\cdot 100:17}{100}}={230\cdot 100:17}\%={100\cdot 230:17}\%\approx 1352{,}94\%$

da hundertstel genau Prozent bedeutet.

Wir haben in diesem Fall tatsächlich die Prozentrechnung mit Hilfe der Schlussrechnung durchgeführt, so wie wir das gelernt haben:

${\begin{matrix}{\text{17 Äpfel}}\\\uparrow :\\{\text{230 Äpfel}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\{}\\x\end{matrix}}$        $\left({\frac {100\cdot 230}{17}}\approx 1352{,}94\right)\qquad x\approx 1352{,}94\%$

230 Äpfel sind daher ca. 1352,94% von 17 Äpfel.

Was ist, wenn man 17% von 35 Stunden berechnen will?

17% bedeutet 17 Hundertstel. Wir müssen 35 Mal die 17 Hundertstel nehmen. Anders gesagt teilen wir die 35 Stunden in Hundert Teile und nehmen 17 davon:

$x=35\cdot {\frac {17}{100}}=5{,}95$

17% von 35 Stunden sind daher 5,95 Stunden.

Das ist wieder genauso, wie wir den Prozess mit Schlussrechnung gelernt haben:

${\begin{matrix}100\%\\\uparrow :\\17\%\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{35 Stunden}}\\{}\\x\end{matrix}}$        $\left(35\cdot {\frac {17}{100}}={\frac {17\cdot 35}{100}}\right)\qquad x=5{,}95{\text{ Stunden}}$

Ähnlich denkt man bei der Schlussrechnung (genauer: bei der direkten Proportionalität). Nehmen wir folgendes Beispiel:

3,5 Liter eines Stoffes wiegen 14,7 kg.

a) Wie viel wiegen 175 Liter?

b) Wie viel Liter sind 3850kg?

Für die erste Frage denkt man erst, wie viel ein Liter wiegt. Man soll also 14,7 kg durch 3,5 dividieren, um zu finden, wie viel jedes Liter wiegt. Das ist als ob man eine Schokolade hätte und wissen wollte, wie viel jedes Teil wiegt.

$x_{1}={\frac {14{,}7}{3{,}5}}=4{,}2$

4,2 kg wiegt jedes Liter des Stoffes.

175 Liter wiegen dann 735 kg:

$175\cdot 4{,}2=735$

Als Schlussrechnung:

${\begin{matrix}{\text{3,5 Liter}}\\\\{\text{175 Liter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\{}\\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$        $\left(175\cdot {\frac {14{,}7}{3{,}5}}\right)\qquad x=735{\text{ kg}}$

In der zweiten Frage muss man erst finden, wie viel Volumen ein kg hat:

$x_{1}={\frac {3{,}5}{14{,}7}}\approx 0{,}238$

Ca. 0,238 Liter ist jedes kg des Stoffes.

Das Volumen von 3850 kg ist dann ca. 917 Liter:

$3850\cdot 0{,}238...=3850\cdot {\frac {3{,}5}{14{,}7}}=916{,}{\dot {6}}$

Nochmal als Schlussrechnung:

${\begin{matrix}{\text{14,7 kg}}\\{}\\{\text{3850 kg}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\{}\\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{3,5 Liter}}\\\\x\end{matrix}}$        $\left(3850\cdot {\frac {3{,}5}{14{,}7}}=916{,}{\dot {6}}\right)\qquad x=916{,}{\dot {6}}{\text{ Liter}}$

Bei der indirekten Prportionalität muss man ein bisschen anderes denken:

• 3 Arbeiter brauchen 15 Stunden, um ein Haus mit Fliesen zu verlegen. Wie viel Zeit brauchen dann 5 Arbeiter?

1 Arbeiter würde in diesem Fall mehr Zeit brauchen. Es gibt für einen Arbeiter viel mehr Boden zu verlegen, wenn er alleine arbeitet. Also weniger Arbeiter brauchen mehr Zeit. Wie wir schon im entsprechenden Kapitel erklärt haben, ist das keine direkte sondern eine indirekte Proportionalität. Man muss in diesem Fall herausfinden, wie viel Zeit ein Arbeiter braucht. Ein Arbeiter wird die Arbeit von allen anderen erledigen müssen und jede der 3 Arbeiter braucht 15 Stunden. Einer Arbeiter braucht daher 45 Stunden:

$3\cdot 15=45$

Wenn jetzt diese Arbeit auf 5 Arbeiter aufgeteilt wird, wird jeder ein fünftel der Arbeit erledigen müssen. Wenn alle zusammen arbeiten, dann wird die Arbeit 9 Stunden dauern:

$45:5=9$

In diesem Fall muss man also direkt gegenüber multiplizieren, wie wir das gelernt haben:

${\begin{matrix}{\text{3 Arbeiter}}\\\downarrow :\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}{\dot {\longleftarrow }}\\\\{}\end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$      $\left({\frac {15\cdot 3}{5}}\right)\qquad x=9\ {\text{Stunden}}\ \$

Zinsen und Kapitalertragssteuer (KESt.)

Zinsrechnung Begriffe

Die Symbole: Guthaben G₀ (Geld im Konto am Anfang), Zinsen Z, effektive Zinsen eZ, Zinssatz Zs, effektiver Zinssatz eZs, Guthaben G₁ (Geld am Ende des ersten Jahres).

Der Begriff Zinsen hat mit den Bankinstitutionen zu tun, der Begriff KESt. mit dem Staat. Eine Bank ist eine Institution, die Geschäfte mit Geld macht. Als Privatkunde kann jede Person ihr Geld in einer Bank anlegen. Das Geld befindet sich dann auf einem sogenannten Konto. Die Bank gibt dem Kunden Zinsen, die nach einem jährlichen Prozentsatz, den sogenannten Zinssatz berechnet wird. Der Grundwert für den Zinssatz ist das Guthaben am Anfang G₀. Die Zinsen werden durch die Staat versteuert. Diese Steuer, Kapitalertragssteuer (KESt.) genannt, ist im deutschsprachigem Raum ca. 25% der Zinsen und dieser Prozentsatz wird im Folgenden immer benutzt.

Es gibt verschiedene Gründe, warum die Bank jedes Jahr den Kunden Zinsen gibt. Einerseits verliert das Geld durch die Inflation (Erhöhung der Preise) an seinen Wert, andererseits erzielen die Banken durch Investitionen und Kredite einen Gewinn, der ein Vielfaches der Zinsen ist.

Wie schon erwähnt, die Zinsen werden versteuert, daher bleiben im Ḱonto nicht die ganzen Zinsen, die die Bank gibt, sonder ein Teil davon, die sogenannten effektiven Zinsen. Da die Steuer 25% ist, sind die effektiven Zinsen der Rest 75% der Zinsen, die die Bank gibt (75% ist das 0,75-fache oder $\textstyle {\frac {3}{4}}$ der Zinsen.

Guthaben am Anfang G₀ ist das Geld, das ein Privatkunde in ein Bankkonto anlegt.

Zinsen Z ist das Geld, das die Bank jedes Jahr dem Kunden dazu gibt, sozusagen als Belohnung für sein Vertrauen an der Bank (und als Teil des Gewinns, den die Bank mit diesem Geld macht).

Zinssatz Zs ist ein Prozentsatz. Er wird benutzt, um die Zinsen, die die Bank gibt, zu berechnen. In diesem Fall ist das Guthaben am Anfang (für das erste Jahr G₀) der Grundwert (also 100%).

Kapitalertragssteuer KESt. ist eine Steuer auf die Zinsen. Sie wird vom Staat genommen, um Funktionen des Staates zu finanzieren. in diesem Buch wird sie immer 25% sein. Der Grundwert allerdings ist in diesem Fall nicht das Guthaben am Anfang, sondern die Zinsen Z, die die Bank dem Kunden gibt.

Effektive Zinsen eZ ist das Geld, das dem Kunden von den Zinsen übrig bleibt, nachdem die Zinsen versteuert werden. Wenn nichts Anderes auf dem Konto passiert, ist das Guthaben nach einem Jahr G₁ die Summe des Guthabens am Anfang G₀ und der effektiven Zinsen.

Effektiver Zinssatz eZs ist ein Prozentsatz. Er ist 75% (also das 0,75-fache oder $\textstyle {\frac {3}{4}}$) des Zinssatzes Zs, da 25% der Zinsen als KESt. vom Staat genommen werden. Wenn nichts Anderes auf dem Konto passiert, wird das Guthaben nach einem Jahr G₁ um so viel mehr Prozent als das Guthaben am Anfang G₀, wie der effektive Zinssatz.

G1 = G0 + eZ	$\textstyle \mathbf {{\text{Z=G}}_{0}\cdot {\frac {\text{Zs}}{100}}}$	KESt.= Z ⋅ $\textstyle \mathbf {\frac {25}{100}}$	eZs= Zs ⋅ $\textstyle \mathbf {\frac {75}{100}}$= Zs ⋅ $\textstyle \mathbf {\frac {3}{4}}$
eZ = Z – KESt.	$\textstyle \mathbf {{\text{eZ=G}}_{0}\cdot {\frac {\text{eZs}}{100}}}$	G1 = G0 · $\textstyle \mathbf {\frac {100+eZS}{100}}$	eZ= Z ⋅ $\textstyle \mathbf {\frac {75}{100}}$= Z ⋅ $\textstyle \mathbf {\frac {3}{4}}$

Zinsen

Wenn man Geld auf einem Konto hat, bekommt man jedes Jahr Zinsen. Die Bank benutzt das Geld vom Konto, um es zu investieren. Teil des Gewinns aus den Investitionen bekommt der Kontoinhaber als Zinsen (zu diesem Thema lernen wir mehr im Kapitel über Wachstum).

Die Zinsen werden nach einem Jahreszinssatz berechnet. Wenn man z.B. 4000€ im Konto (Anfangswert: 100%) hat und der Zinssatz 0,5%, dann bekommt man am Ende des Jahres:

${\begin{matrix}100\%\\\uparrow :\\0{,}5\%\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{4000€}}\\{}\\x\end{matrix}}$        $x=20{\text{€ }}$Zinsen.

KESt., effektive Zinsen, Guthaben nach einem Jahr

Wenn man ein Bankkonto hat, bekommt man von der Bank jedes Jahr Zinsen. Diese werden vom Staat versteuert. Diese Steuer nennt man Kapitalertragssteuer (KESt.). Der Zinssatz für die Berechnung der Steuer ist ungefähr auch 25%. Das bedeutet im vorherigen Beispiel, dass ein Teil (25%) von den 20€ dem Staat (und nicht dem Kontoinhaber) gegeben wird. Wie viel Geld gelangt dann auf das Konto? In dieser Frage sind die Zinsen (und nicht das Geld am Anfang) der Grundwert (also 100%):

${\begin{matrix}100\%\\\uparrow :\\25\%\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{20€}}\\{}\\KESt.\end{matrix}}$      $KESt.=5{\text{€}}$  KESt.

Daher bleiben auf dem Konto nicht 20€ mehr am Ende des Jahres sondern:

${\begin{matrix}100\%\\\uparrow :\\75\%\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{20€}}\\{}\\eZ.\end{matrix}}$      $\qquad eZ.=15{\text{€}}$  effektive Zinsen.

(nicht vergessen: $\textstyle 25\%=0,25={\frac {25}{100}}={\frac {1}{4}},\qquad 75\%=0,75={\frac {75}{100}}={\frac {3}{4}}$,  also 3/4 der Zinsen bleibt im Konto und 1/4 geht zum Staat als Steuer KESt.)

Diese Zinsen, die auf dem Konto bleiben, nennt man effektive Zinsen, den entsprechenden Zinssatz, effektiven Zinssatz. Man kann die effektiven Zinsen offenbar auch einfacher berechnen: eZ = Z – KESt.=20€−5€=15€

Das bedeutet dann, dass das Geld am Ende des Jahres (Guthaben G₁):

G₁=4000€+15€=4015€ ist.

Man kann dann als Formel schreiben:

Die Symbole: Guthaben G₀ (Geld im Konto am Anfang), Zinsen Z, effektive Zinsen eZ, Zinssatz Zs, effektiver Zinssatz eZs, Guthaben G₁ (Geld am Ende des ersten Jahres).

G1 = G0 + eZ	Z = G0 · Zs : 100	KESt.= Z ⋅ $\textstyle {\frac {25}{100}}$	eZs= Zs ⋅ $\textstyle {\frac {75}{100}}$= Zs ⋅ $\textstyle {\frac {3}{4}}$
eZ = Z – KESt.	eZ = G0 · eZS : 100	G1 = G0 · $\textstyle {\frac {100+eZS}{100}}$	eZ= Z ⋅ $\textstyle {\frac {75}{100}}$= Z ⋅ $\textstyle {\frac {3}{4}}$

Geometrie der Ebene

Definitionen der ebenen Geometrie

Grundbegriffe der Geometrie

Strecke

Strecke Definition

Strecke ist der kürzeste Weg zwischen zwei Punkten. Z.B von den beiden gezeichneten Möglichkeiten zwischen A und B im Bild "Strecken Definition", welche ist die kürzeste?

Gerade und Strahl

Gerade und Strahl

Wenn ich eine Strecke auf einer Seite unendlich lang verlängere, dann habe ich einen Strahl. Wenn ich das an beiden Seiten tue, dann hab ich eine Gerade.

Winkel

Winkel Darstellung

Zwischen zwei Strahlen, die vom gleichen Punkt ausgehen, entsteht ein Winkel. Mit einem Winkel misst man eine Drehung.

Rechter Winkel

vier rechte Winkel

Wenn sich zwei Geraden einander so schneiden, dass vier gleichen Winkel entstehen, dann ist jeder von diesen Winkeln ein rechter Winkel.

Parallelen

zwei Parallele Geraden

Wenn zwei Geraden so nebeneinander liegen, dass sie nie einander schneiden und immer den Gleichen Abstand haben, dann sind sie parallel zueinander.

Punkt

Um alle Begriffe bisher zu definieren, haben wir den Punkt gebraucht. Was ist aber wieder ein Punkt? Diese ist die schwerste Definition. Wenn man beispielsweise den Abstand zwischen Wien und Linz berechnen will, muss man einen Ort in jeder Stadt wählen, sonst kann der Abstand bis 15km mehr oder weniger sein! Dieser Ort könnte z.B. eine Säule in der Mitte von jeder Stadt sein. Für so einen großen Abstand reicht eine Säule schon. Sie ist sozusagen ein Punkt.

Wenn man aber die Säule selber messen will, geht es nicht mehr. Man nimmt dann zwei winzigen Flächen am Rand der Säule. Je kleiner das Objekt ist, das wir messen wollen, desto kleiner muss der „Punkt“ sein.

Im idealen Fall ist der Punkt gar nichts, hat selber keine Länge, keine Breite und keine Höhe! So kann man sich einen Punkt vorstellen und so wird er auch definiert.

Eckpunkt

Seite und Diagonale

Die Seiten einer ebenen Figur sind die Abgrenzungen der Figur vom Rest der Ebene. Im folgenden Bild eines Quadrats werden alle seine Seiten mit a bezeichnet, im Bild des Rechtecks werden zwei Seiten mit a und zwei mit b bezeichnet. Eine Seite verbindet zwei Punkte die nacheinander liegen. Die Diagonale verbindet hingegen zwei gegenüberliegenden Eckpunkte, die sich nicht am Rand der gleichen Seite befinden. Ein Quadrat und ein Rechteck haben jeweils zwei Diagonalen, die gleich lang sind, in einem Parallelogramm hingegen sind sie nicht gleich lang.

Figuren

Quadrat

Quadrat

Ein Quadrat ist eine viereckige geschlossene Figur, deren Seiten als auch deren Winkel gleich zu einander sind. Formeln: u=4a, A=a² (u ist der Umfang, a die Seite, A die Fläche). Mit d ist hier die sogenannte Diagonale gezeigt (verbindet zwei gegenüberliegende Eckpunkte).

Rechteck

Rechteck

Ein Rechteck ist eine viereckige geschlossene Figur, deren Winkel gleich zueinander sind und deren gegenüberliegenden Seiten auch gleich sind. Formeln: u=2a+2b oder u=2(a+b), A=a·b. Mit d ist wieder die Diagonale bezeichnet, mit a und b die Seiten (in der Figur ist a für die Länge, also die längere Seite und b für die Breite, also die kürzere Seite).

Parallelogramm

Parallelogramm

Ein Parallelogramm ist eine viereckige geschlossene Figur, deren gegenüberliegenden Seiten gleich sind. Daher sind sie auch parallel. Formeln: u=2a+2b oder u=2(a+b), A=a·h_a oder A=b·h_b. In der Figur ist h_a die Höhe zur Seite a und h_b die Höhe zur Seite b. Mit d wird eine der beiden Diagonalen bezeichnet (hier die kürzeste).

Raute (Rhombus)

Rhobus

Eine Raute ist eine viereckige geschlossene Figur, deren Seiten gleich sind. Daher sind auch alle Winkeln gleich. Formeln: u=4a, A=$\textstyle {\frac {e\cdot f}{2}}$. Mit e und f sind die beiden Diagonale bezeichnet, mit a die Seite.

Trapez

Trapez

Ein Trapez ist eine viereckige geschlossene Figur mit zwei gegenüberliegenden parallele Seiten. Formeln: u=a+b+c+d, $\textstyle A={\frac {a+c}{2}}\cdot h$. Mit a, b, c und d werden die vier (nicht unbedingt gleichen) Seiten bezeichnet, mit h die Höhe auf die Basis (Basis ist nicht nur beim Trapez, sondern bei jeder Figur die untere Seite, beim Trapez im Bild hier die Seite a, also die Seite die im Bild unten steht). In der Figur sieht man auch die Diagonalen (ohne Symbol).

Deltoid

Deltoid1

Ein Deltoid ist eine viereckige geschlossene Figur mit zwei Paaren nacheinander liegenden gleichen Seiten.

Vieleck (regelmäßiges)

Siebeneck

Ein Vieleck ist eine Figur mit mehreren Winkeln. Wenn die Figur geschlossen ist und alle Seiten (und Winkel) gleich zueinander, dann ist das Vieleck regelmäßig. Im Bild sieht man ein regelmäßiges Siebeneck, die Seite ist hier mit s bezeichnet.

Fragen zu Figuren

Ist jedes Rechteck ein Parallelogramm? Umgekehrt?

Ist jede Raute ein Quadrat? Umgekehrt?

Ist jedes Trapez ein Parallelogramm? Umgekehrt?

Ist jedes Quadrat auch ein Rechteck? Umgekehrt?

Dreieck, Besondere Dreiecke

• 
  spitz
• 
  gleichseitiges
• 
  gleichschenkliges
• 
  rechtwinkeliges
• 
  stumpfwinkeliges

Ein Dreieck ist eine geschlossene Figur mit drei Winkel. Ist einer Winkel mehr als 90°, dann heißt das Dreieck stumpfwinkeliges, wenn alle Winkel kleiner als 90° sind, dann spitzwinkeliges.

Bei allen Dreiecken gilt für den Umfang: u=a+b+c, wobei a, b und c die Symbole für die Seiten sind. Die allgemeinen Formeln für die Fläche sind  $\textstyle A={\frac {a\cdot h_{a}}{2}}={\frac {b\cdot h_{b}}{2}}={\frac {c\cdot h_{c}}{2}}$, wobei h_a, h_b und h_c die Höhen zu den entsprechenden Seiten sind (im Bild nicht zu sehen).

Ist einer der Winkeln 90°, dann wird das Dreieck rechtwinkelig genannt. Die Formel für die Fläche ist in diesem Fall  $\textstyle A={\frac {a\cdot b}{2}}$, wobei hier a und b die kleineren Seiten sind (Katheten genannt). Die größte Seite (dem rechten Winkel gegenüber) nennt man Hypotenuse.

Sind zwei der drei Winkel (und auch zwei Seiten) gleich, dann nennt man das Dreieck gleichschenklig. Sind alle Winkel (und Seiten) gleich, dann ist es ein gleichseitiges Dreieck (mit Seite a). Für die Fläche des gleichseitigen Dreiecks gilt:  $\textstyle A={\frac {\sqrt {3}}{4}}\cdot a^{2}$.

Intuitiver Beweis der Formeln des Flächeninhalts mancher ebenen Figuren

Definition des Quadratzentimeters

1 cm²

Ein Zentimeter Quadrat (1 cm², ein Zentimeter hoch zwei) ist ganz einfach ein Quadrat, dessen Seite ein Zentimeter ist (erstes Bild).

Fläche des Rechtecks

Rechteck

Im zweiten Bild sieht man ein Rechteck, dass aus mehreren Quadrat Zentimeter besteht. Hier haben wir zwei Zeilen, jede mit 3 Quadraten. Insgesamt 2x3=6 (cm²). Man kann offenbar sagen, dass der Flächeninhalt A eines Rechtecks die Länge a der einer Seite mal die Länge b der anderen ist.

A = a · b

Sonderfall: Das Quadrat. Da gilt A = a · a = a², da die Seiten gleich sind.

Fläche des Parallelogramms

Parallelogramm

Im Fall eines Parallelogramms kann man sich vorstellen, dass ein Stück der Figur so wie im Bild geschnitten und auf der anderen Seite wieder hinzugefügt werden kann. Dadurch entsteht wieder ein Rechteck, dessen Seiten jetzt die Basis a und die Höhe h_a des Parallelogramms sind. Die Fläche des dadurch entstandenen Rechtecks ist daher der Flächeninhalt des Parallelogramms:

A= a · h_a

Fläche des Dreiecks

Fläche des Dreiecks

Im Fall eines Dreiecks kann man sich wie im Bild vorstellen, dass ein zweites Dreieck, gleich groß wie das erste, umgedreht und auf das erste zugefügt wird. So entsteht wieder ein Parallelogramm, dessen Flächeninhalt A = b · h_b ist. Weil aber dieses Parallelogramm aus 2 gleiche Dreiecke besteht, muss man für den Flächeninhalt des Dreiecks das ganze mit 2 dividieren:

$A={\frac {b\cdot h_{b}}{2}}$

Entsprechend für die anderen Seiten kann man schreiben:

$A={\frac {a\cdot h_{a}}{2}}$

$A={\frac {c\cdot h_{c}}{2}}$

Sonderfälle: Rechtwinkeliges, gleichschenkeliges und gleichseitiges Dreieck. In den zwei letzten Fällen kann man den Satz des Pythagoras benutzen, um eine Formel zu erzeugen (machen wir aber hier nicht).

Fläche des Trapezes

Fläche des Trapezes

Genauso geht man bei einem Trapez vor. Es entsteht ein Parallelogramm, dessen Basis aber jetzt a+b ist und den Flächeninhalt daher (a+b) · h. Weil, wie vorher beim Dreieck, das Trapez zwei mal vorkommt, muss man wieder für den Flächeninhalt des Trapezes das ganze durch 2 dividieren:

$A={\frac {a+c}{2}}\cdot h$

Anwendung der Formeln

Variablen in der Geometrie

Bei allen Formeln gibt es sogenannten „Variablen“. Es geht in der Regel um ein Buchstabe, der für irgendwas steht. Hier schreiben wir, wofür diese Symbole in der Geometrie stehen.

• Ein großes A, steht in der Regel für die Fläche (genauer für den Flächeninhalt)

• Ein u steht i.d.R. für den Umfang (also wie lang das Rum-herum der Figur ist)

• a, b, c usw. stehen i.d.R. für die Seiten (auch Länge oder Breite) von Figuren

• h (oder H) steht i.d.R. für die Höhe einer Figur. Oft gibt es dann ein Index, z.B. h_b, was dann bedeutet, dass diese die Höhe für die Seite b ist.

• r (oder R) steht i.d.R. für den Radius eines Kreises.

• d steht bei einem Kreis für den Durchmesser des Kreises, bei einem Parallelogramm (oder Rechteck, Quadrat, Trapez, Vieleck) aber für die Diagonale!

• Griechische kleine Buchstaben (α, β, γ, δ, ε, θ, φ) stehen i.d.R. für Winkel.

• Allerdings ist mit dem griechischen Buchstabe π die Kreiszahl bezeichnet (π≈3,1415...).

Formel Einsetzen in der ebenen Geometrie

Bei einer Aufgabe sind immer gewisse Informationen gegeben, z.B.:

• Ein Zimmer ist 4m lang und 2,8m breit. Finden Sie seinen Umfang und seine Fläche heraus!

In solchen Problemen soll man die gegebenen Zahlen in die Formel sinnvoll einsetzen. Das bedeutet, dass man die Buchstaben in der Formel durch Zahlen ersetzt. In diesem Beispiel sucht man in einer Formelsammlung das Rechteck (da ein Zimmer die Form eines Rechtecks hat).

Rechteck

In der Figur, die man in der Formelsammlung finden kann, kann man sehen, dass mit a die Länge und mit b die Breite bezeichnet wird. In der Formelsammlung kann man auch die Formel für den Umfang finden:

u=2a+2b

Die Länge a ist gegeben: 4m. Die Breite b auch: 2,8m. Wenn nichts zwischen einer Zahl und einer Variable steht (hier z.B. 2a), dann ist mal gemeint (2 mal a). Man schreibt also an der Stelle von a und b die Zahlen 4 und 2,8:

$u=2a+2b=2{\cancel {a}}^{=4}+2{\cancel {b}}^{=2{,}8}=2\cdot 4+2\cdot 2,8=13,6\ (m$, da wie m mit m addiert haben)

In der Spalte für die Fläche steht beim Rechteck:

A=a·b   also

$A=a\cdot b={\cancel {a}}^{=4}\cdot {\cancel {b}}^{=2{,}8}=4\cdot 2,8=11,2\ (m^{2}$, da wie m mit m multipliziert haben)

Man soll auch auf die Einheiten aufpassen:

Der Umfang ist eine Strecke, also er wird in Streckeneinheiten gemessen (hier m), die Fläche hingegen in Flächeneinheiten (hier in m²).

Andererseites kann es sein, dass eine Größe in verschiedenen Einheiten gegeben wird, z.B.:

• Die Länge eines Rechtecks ist 5dm und seine Breite 32cm. Finden Sie seinen Umfang und seine Fläche heraus!

Das Einsetzen von Werten in einer Formel setzt voraus, dass die Einheiten übereinstimmen. Man muss z.B. überall in der Formel Werte in Stunden haben und nicht irgendwo Stunden, an einer anderen Stelle Minuten usw. Hier muss man den Wert einer der beiden Seiten umwandeln, z.B.:

32cm=32:10 dm = 3,2 dm

Jetzt sind beide Seiten (Länge und Breite) in dm und es kann weiter berechnet werden:

u=2a+2b und A=a·b

Die Länge a ist gegeben: a=5dm. Die Breite b haben wir jetzt auch in dm umgerechet: b=3,2dm:

$u=2a+2b=2{\cancel {a}}^{=5}+2{\cancel {b}}^{=3{,}2}=2\cdot 5+2\cdot 3{,}2=16{,}4\ (dm$, da wie hier dm mit dm addiert haben)      und

$A=a\cdot b={\cancel {a}}^{=5}\cdot {\cancel {b}}^{=3{,}2}=5\cdot 3{,}2=16\ (dm^{2}$,da wie hier dm mit dm multipliziert haben)

Hätten wir die Einheiten (die 32cm) nicht umgewandelt, hätten wir Probleme mit dem Einheit am Ende oder sogar ein völlig falsche Antwort:

• Bei der Multiplikation hätten wir:

$\textstyle A=a\cdot b={\cancel {a}}^{=5}\cdot {\cancel {b}}^{=32}=5\cdot 32=160\qquad$FALSCH! Wenn man hier dm² oder cm² als Einheit schreibt, ist das Ergebnis völlig falsch, die Einheit, die wir schreiben hätten sollen, wäre dm⋅cm, das wäre zwar richtig, aber diese Einheit wird für die Fläche nie benutzt.

• Bei der Addition hätten wir:

$u=2a+2b=2{\cancel {a}}^{=5}+2{\cancel {b}}^{=32}=2\cdot 5+2\cdot 32=74\qquad$FALSCH! Hier ist sogar der Wert völlig falsch! Der richtige Wert, wie wir gesehen haben, ist 16,4 dm (oder 164 cm). Man kann nicht dm und cm addieren oder subtrahieren, genauso wie man nicht dm und kg addieren kann! Addieren (oder subtrahieren) kann man nur Sachen, die genau die gleichen Einheiten haben!

Nicht nur bei Multiplikation oder Addition müssen die Einheiten übereinstimmen, sondern auch bei Division und allen anderen Rechenarten. Bei Multiplikation und Addition haben wir das Beispiel gerade eben gesehen (Fläche und Umfang des Rechtecks am letzten Beispiel). Ein Beispiel für Division, ist wenn man die Fläche eines Rechtecks durch seine Länge dividiert, um die Breite zu berechnen. Wenn die Fläche 6cm² und die Länge 30mm, dann kann man NICHT die Division so durchführen:  $\textstyle b={\frac {6}{30}}$, da 6 in cm gegeben ist und 30 in mm. Man soll zuerst z.B. die mm in cm umwandeln (30mm=3cm) und dann die Division durchführen:  $\textstyle b={\frac {6}{3}}=2$ (das sind dann cm, da wir cm² durch cm dividiert haben und man die Hochzahl und dann kann man die Einheiten kürzen:  $\textstyle {\frac {cm^{\cancel {2}}}{\cancel {cm}}}=cm$.

Wir können also schreiben:

Bei Rechnungen müssen die Einheiten immer übereinstimmen!

Bei einer Rechnung (oder Gleichung) muss man immer erst kontrollieren, ob die Einheiten übereinstimmen, dann die Einheiten, die nicht übereinstimmen, in übereinstimmenden Einheiten umwandeln und erst am Ende die Rechnung durchführen! Das gilt immer (auch bei der Schluss-und Prozentrechnung)!

In Physik benutzt man sogar Einheitssysteme, das ist aber für dieses Buch ein fortgeschrittenes Thema.

Umformen in der ebenen Geometrie konkret

Beim Umformen haben wir am Anfang eine Formel, in der eine bestimmte Variable durch eine Beziehung von anderen Variablen und Zahlen ausgedrückt wird. Diese bestimmte Variable steht allein auf einer Seite (i.d.R. die rechte). Diese Formel wird dann so geändert, dass eine andere Variable der Formel allein auf einer Seite steht. Dafür benutzen wir u.A. die Gegenrechnungen (siehe Kapitel „Umformen“). Z.B. ist plus die Gegenrechnung von minus (und umgekehrt), mal von plus (und umgekehrt), Wurzel von Quadrat (und umgekehrt). „Konkret“ wird in diesem Buch das Umformen dann genannt, wenn die Variablen (außer einer) durch Zahlen ersetzt werden. Wenn dies nicht der Fall ist, wird die Rede von „abstraktem“ Umformen sein. Im letzten Fall bleiben alle Variablen (alle „Buchstaben“) vorhanden. Hier zwei Beispiele aus der Geometrie der Ebene:

Der Umfang eines Quadrats ist 12cm. Berechnen Sie die Seite und die Fläche!

Wir finden die Figur (hier Quadrat) in der Formelsammlung. Wir fangen mit der Formel der gegebenen Eigenschaft (hier Umfang) an:

u=4a

Hier ist der Umfang gegeben, man braucht die Seite. Zwischen 4 und a steht nichts, also ist mal gemeint. Die Gegenrechnung von mal ist durch und der Umfang ist 12, also:

$u=4a\quad |:4$

${\frac {u}{4}}=a$    Seiten in einer Gleichung kann man selbstverständlich umtauschen, also:

$a={\frac {u}{4}}={\frac {\cancelto {12}{u}}{4}}={\frac {12}{4}}$  also

a=3 cm

Die Formel für die Fläche, die man auch in der Formelsammlung finden kann ist dann:

$A=a^{2}$$_{(a=3)}\ \$$=3^{2}=9$   also  $A=9\ cm^{2}$

Auch wenn die Seite erst nicht gefragt wäre, wäre es doch notwendig diese erst einmal zu berechnen, um dann mit Hilfe des Wertes für die Seite auch die Fläche berechnen zu können.

Ähnlichkeit von Figuren

Wenn wir die beiden Bilder oben vergleichen, können wir sagen, dass es das gleiche Dreieck ist, nur von einem anderen Abstand gesehen oder, dass wir doch zwei verschiedene Dreiecke haben, die zwar ähnlich zueinander sind aber doch nicht das gleiche Dreieck, da die Seiten nicht gleich sind. Um auf diesen Unterschied aufmerksam zu machen, wird beim Vergleich zwei geometrischen Figuren nicht das Wort "gleich" (und "nicht gleich") benutzt, sondern die Worten "ähnlich" (und "nicht ähnlich") und "kongruent" (und "nicht kongruent").

Zwei geometrische Figuren sind ähnlich, wenn sie die gleiche Seitenanzahl haben und alle entsprechenden Winkel gleich zueinander sind. Wenn dazu zumindest eine Seite (und daher auch alle andere) der beiden Figuren gleich ist, dann sagt man, dass die Figuren kongruent sind.

Das Wort "gleich" wird bei geometrischen Figuren nicht benutzt, weil es dann nicht klar ist, ob nur alle Winkel oder doch auch alle Seiten gleich sind.

Bei ähnlichen Figuren gilt, dass das Verhältnis entsprechender Seiten eine Konstante Zahl ist. Wenn wir die Seiten aus dem Bild benutzen, wird es klar, was damit gemeint ist. Nehmen wir die Seite b aus dem Bild links und die entsprechende Seite b' aus dem Bild rechts. Verhältnis in Mathematik bedeutet Bruch. Der Bruch der beiden Seiten ist dann $\textstyle {b \over {b'}}$. Werden die beiden Seiten in irgendeiner Weise gemessen, wird dann festgestellt, dass der Bruch ca. 1,5 ist. Es gilt also: $\textstyle {b \over {b'}}=1{,}5$.

Wenn wir ein anderes Paar von entsprechenden Seiten nehmen, wird das Verhältnis (der Bruch) wieder 1,5 sein: $\textstyle {c \over {c'}}=1{,}5$.

Das Verhältnis (der Bruch) von entprechenden Seiten (z.B. $\textstyle {b \over {b'}}$ oder $\textstyle {c \over {c'}}$) ist eine konstante Zahl, hier 1,5. Das gilt genauso für das dritte Paar von entsprechenden Seiten: $\textstyle {d \over {d'}}=1{,}5$.

Diese Regel gilt nicht nur in Dreiecken sondern in allen geometrischen Figuren, die ähnlich sind. Im folgenden Bild sieht man verschiedene Figuren. Alle Figuren mit der gleichen Farbe sind ähnlich.

Alle hier gleichfarbigen Figuren sind zueinander ähnlich.

Strahlensatz

Die Ähnlichkeit von Figuren findet Anwendung im sogenannten "Strahlensatz".

Nehmen wir zwei geraden, die einander am Schnittpunkt Z schneiden, wie die Geraden BB' und AA' im Bild links. Diese Geraden werden von zwei weiteren parallel zueinander Geraden AB und A'B' geschnitten. So entstehen zwei ähnliche Dreiecke, ABZ und A'B'Z. Da die Dreiecke ähnlich sind, gilt:

${\frac {AB}{A'B'}}={\frac {AZ}{A'Z}}={\frac {BZ}{B'Z}}$

Diese Formel zeigt, was bei der Ähnlichkeit von Figuren behauptet wurde: Das Verhältnis (der Bruch) von entsprechenden Seiten bleibt konstant.

Der Strahlensatz findet zahlreiche Anwendungen in Physik und Mathematik. Hier erwähnen wir "nur" seine Anwendung bei der Vermessung des Abstandes zwischen Mond und Erde.

Eine Bemerkung dazu: Das erste in der Geschichte bekanntes Buch, in dem Geometrie als auf wenigen Sätzen aufgebautes geordnetes Wissen dargestellt wird, ist das Werk "Elemente" von Euklid. In diesem Werk wird erst der Strahlensatz bewiesen und dann auf die Ähnlichkeit von Figuren angewendet.

Zusammengesetzte Figuren

Satz von Pythagoras

Geschichte des Satzes von Pythagoras

Obwohl der Satz nach dem griechischen Philosoph Pythagoras genannt wird, wurde er nicht von ihm entdeckt. Der Satz wurde zumindest 1000 Jahre früher benutzt. Es gibt Tontafel aus Babylonien, die sogenannte pythagoreische Tripeln beinhalten. Eine pythagoreische Tripel sind drei Zahlen, die den Satz von Pythagoras erfühlen. Die Entdeckung zeigt eine hochentwickelte antike Zivilisation, Die Berechnungen mancher Tripel ohne technische Mittel sind ziemlich kompliziert und brauchen viel Geduld und Zeit.

Formulierung des Satzes von Pythagoras

Der Satz von Pythagoras lautet:

In einem rechtwinkeligem Dreieck ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse.

Der Satz gilt daher nur bei Dreiecken, die einen rechten Winkel haben.

Selbstverständlich versteht man den Satz viel besser, wenn man eine Figur sieht:

Die Seiten an der rechten Winkel nennt man Katheten (im Bild mit a und b), die Seite gegenüber Hypotenuse (im Bild mit c).Es gilt: $a^{2}+b^{2}=c^{2}$

Nehmen wir drei Zahlen: 2, 3 und 4. Sind diese eine pythagoräische Tripel? Die größte Zahl sollte die längste Seite sein, die Hypotenuse, also c. Hier ist es die Zahl 4. Dann wären die Katheten 2 und 3. Die entsprechenden Quadrate der Katheten sind 2²=4 und 3²=9, ihre Summe 4+9=13. Das Quadrat der Hypotenuse wäre 4²=16. Es gilt 2²+3²≠4² (13 ist nicht gleich 16!). Das bedeutet: Es gibt kein rechtwinkeliges Dreieck, dessen Katheten 2 und 3 und dessen Hypotenuse 4 Einheiten (z.B. Meter) sind.

2,3 und 4 sind daher keine Pythagoreische Tripel. Wie ist es mit 3, 4 und 5? Sind diese Zahlen eine Pythagoräische Tripel?     3²+4² = 25   aber auch 5² = 25.  Es gilt also: 3²+4²=5².  Das bedeutet nicht nur, dass es ein rechtwinkeliges Dreieck gibt, dessen Katheten 3 und 4 und dessen Hypotenuse 5 Einheiten ist, sondern auch umgekehrt, dass ein Dreieck, dessen Seiten 3, 4 und 5 Einheiten sind, einen rechten Winkel haben muss!

In den Aufgaben muss man aufpassen. Wenn die Katheten angegeben sind und die Hypotenuse gefragt, dann kann man die gegebene Formel benutzen:

• Bei einem rechtwinkeligen Dreieck sind die Katheten 6 und 8 cm lang. Berechnen Sie die Hypotenuse!

$a^{2}+b^{2}=c^{2}\qquad$ wobei $a=6$ und $b=8$ also

$6^{2}+8^{2}=c^{2}\ \Rightarrow \ 36+64=c^{2}\ \Rightarrow \ 100=c^{2}\ \Rightarrow \ c={\sqrt {100\ }}=10cm$

Wenn aber die Hypotenuse und eine Kathete gegeben sind, dann muss man die Formel erst umformen:

• Bei einem rechtwinkeligen Dreieck sind die eine Kathete 21mm und die Hypotenuse 0,29dm lang. Berechnen Sie die andere Kathete!

Erst müssen wir auf die Einheiten aufpassen: 0,29dm=29mm

$a^{2}+b^{2}=c^{2}\qquad |-a^{2}$

$b^{2}=c^{2}-a^{2}\qquad |-a^{2}$also$\qquad b^{2}=29^{2}-21^{2}=841-441=400\qquad$$b={\sqrt {400}}=20\ mm$

Also: Wenn beide Katheten angegeben sind müssen wir die Quadrate addieren, wenn nur eine Kathete und die Hypotenuse, müssen wir vom größeren Quadrat das kleinere subtrahieren. In beiden Fällen ziehen wir dann die Wurzel des Ergebnisses.

Geometrie des Raums

Grundbegriffe

Dimension

Wir haben schon in der Geometrie der Ebene den Begriff der Strecke als auch verschiedene Figuren auf einer ebenen Fläche (z.B. Quadrat, Kreis, Dreieck, Rechteck) kennengelernt. Für eine Strecke braucht man nur die Länge angeben (z.B. 2,4dm), dann hat man sie vollständig beschrieben. Alle Strecken mit dieser Länge sind die gleiche Sache (man sagt in Mathematik: Sie sind Kongruent).

Verschiedene Rechtecke
mit gleicher Länge
und anderer Breite

Bei einem Rechteck hingegen reicht die Länge nicht aus. Es gibt unendlich viele Rechtecke mit der gleichen Länge und eine andere Breite. Diese Rechtecke sind nicht mehr die gleiche Sache. Sie haben auch einen anderen Flächeninhalt. Sie sind nicht kongruent. Man braucht daher bei Flächen zwei Zahlen, die Abstände beschreiben, beim Rechteck ist das die Länge und die Breite.

Quader mit Raumdiagonale d

Wenn man jetzt eine Figur im Raum betrachtet, z.B. einen Quader, dann reichen die Länge und die Breite wieder nicht aus. Da braucht man noch einen Abstand, die Höhe. Wenn die Höhe anders ist, dann ist auch das Volumen anders.

Die Anzahl der Abstandswerte, die man braucht, um eine Figur vollständig zu beschreiben, nennt man Dimension.

Eine Strecke ist eine eindimensionale Figur: Allein ein Abstand (die Länge), reicht aus, um sie zu beschreiben. Ein Rechteck (und alle ebene Figuren) ist eine zweidimensionale Figur: Man braucht zwei Abstände (Länge und Breite), um sie zu beschreiben. Ein Quader (und alle Figuren, die Raum besetzen) ist eine dreidimensionale Figur: Man braucht drei Abstände (Länge, Breite und Höhe), um sie zu beschreiben. In unserem Bild eines Quaders wird die Länge mit a, die Breite mit b und die Höhe mit c bezeichnet.

Obwohl wir Menschen uns nicht mehrere Dimensionen vorstellen können, gibt es in der Physik theoretische Modelle, die noch mehrere Dimensionen haben. Beispielsweise setzt die allgemeine Relativitätstheorie die Zeit als eine weitere Dimension des sogenannten Zeitraums voraus! Die Stringtheorie kann sogar 11 Dimensionen voraussetzen!

Körper

Ein Gegenstand in der Geometrie wird Körper genannt, wenn für seine Beschreibung drei Abstände notwendig und hinreichend sind.

Notwendig bedeutet, dass weniger Abstände nicht genügend sind, um den Körper zu beschreiben. Man kann nicht einen Quader nur mit Länge und Breite vollständig beschreiben.

Hinreichend bedeutet, dass man nicht mehrere Abstände oder eine andere Dimension für die Beschreibung braucht. Wenn die Länge, die Breite und die Höhe des Quaders gegeben sind, braucht man nicht auch die Raumdiagonale angeben (sie wird schon von den anderen drei Abständen bestimmt).

Jede dreidimensionale Figur ist ein (geometrischer) Körper. In diesem Text wird auch das Wort „Raumfigur“ dafür benutzt.

Kante

Im Kapitel über die Geometrie der Ebene haben wir den Begriff der Seite einer ebenen Fläche gesehen. Bei einem Quadrat sind alle Seiten gleich, bei einem Rechteck gibt es eine Länge und eine Breite. Die Strecken am Rand einer ebene Figur wurden also Seiten genannt.

Die Strecken am Rand eine Raumfigur werden aber doch Kanten genannt. Das Wort „Seite“ wäre in diesem Fall verwirrend: man wüsste dann nicht, ob mit „Seite“ die Seitenfläche oder die Seitenstrecke gemeint ist. Daher benutzt man das Wort „Kante“ für die Strecken. In unserem Bild eines Quaders wird die Länge mit a, die Breite mit b und die Höhe mit c bezeichnet. a,b und c sind daher Kanten des Quaders. Es gibt in diesem Bild 4 Kanten, die so lang wie a sind, 4 Kanten, die so lang wie b sind, und 4 Kanten, die so lang wie c sind.

Für die ebenen Flächen, die die Figur begrenzen, benutzt man die Worte „Grundfläche“, „Seitenfläche“ und „Deckfläche“. Es gibt selbstverständlich auch Raumfiguren, die von keinen ebenen Flächen begrenzt werden, wie beispielsweise die Kugel.

Ecke und Raumdiagonale

Den Punkt, wo drei Grenzflächen aufeinander treffen, nennt man Ecke (Eckpunkt). Die Strecke zwischen zwei Eckpunkten, die nicht auf der gleichen Grenzfläche liegen, nennt man Raumdiagonale (mit d im Bild des Quaders bezeichnet).

Oberfläche

Grundfläche

Pyramide

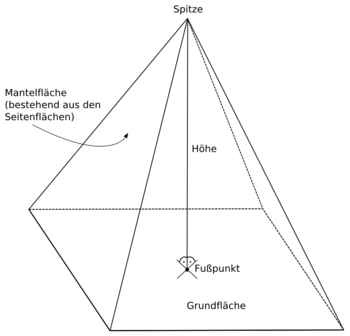
Grundfläche ist die Fläche, die im Bild unten (am Grund) steht. Bei Figuren deren Grenzflächen alle die gleiche Form haben (wie z.B. in einem Quader, wo alle Grenzflächen Rechtecke sind), kann jede beliebige Fläche der Figur als Grundfläche benutzt werden.

Wenn es eine Grenzfläche gibt, die sich von den anderen unterscheidet (wie z.B. bei der Pyramide in unserem Bild: alle Flächen außer einer sind Dreiecke), dann wird i.d.R. diese Fläche als Grundfläche bezeichnet.

Wenn es eine Grundfläche gibt, dann kann ihr gegenüber nur ein Punkt oder eine ganze Fläche stehen. Wenn ihr gegenüber eine ganze Fläche steht, dann nennt man diese Fläche Deckfläche (da sie an der „Decke“ ist). Die Deckfläche kann auch rund sein. Wenn der Grundfläche gegenüber nur ein Punkt liegt (wie in der Pyramide am Bild), dann nennt man diesen Punkt Spitze.

Seitenfläche und Mantel

Wenn es eine Grundfläche gibt, dann nennt man jede der restlichen Flächen Seitenfläche (außer der Deckfläche, wenn es eine gibt). Alle Seitenflächen zusammen nennt man Mantel. Der Mantel kann allerdings auch aus runden und nicht nur ebenen Flächen bestehen, wie z.B. in einem Zylinder (der auch eine Deckfläche hat, die ebenfalls ein Kreis ist) oder einem Kegel (der keine Deckfläche hat, dafür eine Spitze).

Körpernetz

• 
  Netz eines Würfels
• 
  Netz eines Quaders
• 
  Netz eines Prismas
• 
  Netz eines Zylinders
• 
  Netz eines Kegels

Wenn man die Grenzflächen eines Körpers abwickelt, so dass eine (komplizierte) ebene Figur entsteht, dann nennt man diese ebene Figur Körpernetz (oder einfach Netz). Das ist immer möglich, wenn die Grenzflächen ebene Figuren sind, allerdings nicht immer, wenn die Grenzflächen rund sind. Das ist möglich bei einem Quader, einem Zylinder oder einem Kegel aber nicht möglich bei einer Kugel oder einem Torus.

Gerade und schiefe Körper

• 
  A: gerades Prisma
  B: schiefes Prisma
• 
  Gerade Pyramide
• 
  Schiefe Pyramide
• 
  Gerader Kegel
• 
  Schiefer Kegel

Wenn es bei einem Körper eine Grundfläche gibt, dann gibt es gegenüber entweder eine Fläche oder einen Punkt. Wenn der gegenüberliegende Punkt oder der Mittelpunkt der gegenüberliegenden Fläche direkt oberhalb (also senkrecht nach oben) vom Mittelpunkt der Grundfläche liegen, dann sagt man, dass der Körper gerade ist, sonst dass er schief ist.

Raumfiguren

Würfel

• 
  Würfel
• 
  Würfelnetz
• 
  Spielwürfel

Definition

Eine geschlossene Raumfigur, deren Grenzfläche aus 6 kongruente („gleiche“) Quadrate besteht, nennt man Würfel.

Formeln

Mit $a$ wird die Länge der Kante bezeichnet.

Volumen: $V=a^{3}$

Oberfläche: $A_{O}=6a^{2}$

Kantensumme: $K=12a$

Raumdiagonale(rot im Bild): $d_{R}={\sqrt {3}}\ a$

Flächendiagonale(grün im Bild): $d_{F}={\sqrt {2}}\ a$

Quader

• 
  Quader
• 
  Netz eines Quader
• 
  Eine quaderförmige
  Mauerziegel

Definition

Eine geschlossene Raumfigur, deren Grenzfläche aus 3 Paare paarweise kongruente („gleiche“) gegenüberliegende Rechtecke besteht, nennt man Quader.

Formeln

Mit $a$ wird hier die Länge, mit $b$ die Breite und mit $c$ die Höhe bezeichnet (wie im Bild).

Volumen: $V=abc$

Oberfläche: $A_{O}=2ab+2ac+2bc$

Kantensumme: $K=4a+4b+4c$

Raumdiagonale:$d_{R}={\sqrt {a^{2}+b^{2}+c^{2}}}$

Flächendiagonalen: $d_{F1}={\sqrt {a^{2}+b^{2}}}$,  $d_{F2}={\sqrt {a^{2}+c^{2}}}$,  $d_{F3}={\sqrt {b^{2}+c^{2}}}$

Prisma

• 
  Prisma
• 
  Prismanetz
• 
  Optisches Prisma

Definition

Eine geschlossene Raumfigur, die durch Parallelverschiebung eines ebenen Vielecks entlang einer nicht in dieser Ebene liegenden Geraden im Raum entsteht, nennt man Prisma. Die Höhe ist der Abstand zwischen Grund- und Deckfläche.

Formeln

Es gibt viele verschiedenen Prismen, daher sollte man dafür die allgemeineren Formeln benutzen, die sich am Ende dieses Teilkapitels befinden.

Pyramide

• 
  Pyramide
• 
  Pyramidennetz
• 
  Einer der ältesten
  bekannten Pyramiden
• 
  Maya Pyramide

Definition

Wenn man alle Punkte des Umfangs eines Vieleckes mit einem Punkt (genannt „Spitze“ oder „Scheitel“) außerhalb der Ebene des Vieleckes verbindet, dann entsteht die Grenzfläche einer Pyramide. Das Vieleck bildet dann i.d.R. die Grundfläche, die Dreiecke, die durch die Verbindung des Punktes mit dem Umfang entstehen, sind dann die Seitenflächen. Höhe ist der Abstand zwischen Spitze und Grundfläche.

Formeln

Es gibt viele verschiedenen Pyramiden, daher sollte man dafür die allgemeineren Formeln benutzen, die sich am Ende dieses Teilkapitels befinden.

Intuitiver Beweis der Formel des Volumens des Quaders

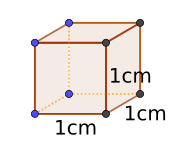
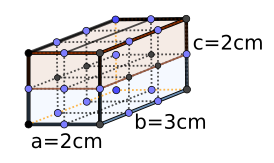
1 cm³ (auch „Kubikzentimeter“ genannt, Bild links) ist ein Würfel, dessen Kante 1cm ist.

Das Wort „Kubik“ stammt aus dem griechischen Wort für Würfel. Als Hochzahl bedeutet „Kubik“ hoch 3, also Kubikzentimeter (cm³), Kubikmeter (m³) usw.

Wie man jetzt im Bild rechts sehen kann, wenn man einen Quader hat, dessen Länge 3cm, dessen Breite 2cm und dessen Höhe 2cm ist, dann beinhaltet dieser Quader 12 Würfel, je 1cm³, also ist das Volumen 12cm³. Man kann daraus folgen, dass das Volumen eines Quaders allgemein die Länge mal die Breite mal die Höhe ist:

$V=a\cdot b\cdot c$

Anwendung der Formeln

Formel Einsetzen in der Raumgeometrie

Holzlineal

Quader

Die Länge eines Lineals ist 3,1 dm, seine Breite 2,5 cm, seine Dicke 2 mm. Berechnen sie die Gesamtlänge seine Kanten, seine Oberfläche und sein Volumen!

Wie wir in der Geometrie der Ebene schon gelernt haben, kann man in solchen Aufgaben das Volumen durch Einsetzen berechnen. Von der Aufgabe kann man schon erschließen, dass das Lineal die Form eines Quaders hat. Hier benutzt man das Wort „Dicke“ anstatt „Höhe“, also wird für diese Dimension ein anderer Name benutzt. Man kann also die Formeln, die in der Formelsammlung für den Quader stehen, benutzen:

Volumen: $V=abc$

Oberfläche: $A_{O}=2ab+2ac+2bc$

Kantensumme: $K=4a+4b+4c=4(a+b+c)$

(Mit $a$ wird hier die Länge, mit $b$ die Breite und mit $c$ die Dicke bezeichnet)

Wie aber schon im entsprechenden Kapitel erwähnt, muss man davor warnen, falschen Einheiten anzuwenden! Die Einheiten muss man erst überprüfen und, wenn notwendig, umwandeln. Das ist in dieser Aufgabe schon der Fall:

$a=3{,}1\,\mathrm {dm} \quad b=2{,}5\,\mathrm {cm} \quad c=2\,\mathrm {mm}$

Wir können alle drei Längenwerte entweder in dm oder in cm oder in mm benutzen. Lass uns hier alle in mm berechnen (wie wir es Kapitel über Einheiten gelernt haben):

$a=3{,}1\,\mathrm {dm} =310\,\mathrm {mm} \quad b=2{,}5\,\mathrm {cm} =25\,\mathrm {mm} \quad c=2\,\mathrm {mm}$

Erst jetzt können wir diese Werte in die Formel einsetzen:

Volumen: $V=abc=310\,\mathrm {mm} \cdot 25\,\mathrm {mm} \cdot 2\,\mathrm {mm} =15500\,\mathrm {mm^{3}}$

Oberfläche: ${A_{O}=2ab+2ac+2bc=2\cdot 310\,\mathrm {mm} \cdot 25\,\mathrm {mm} +2\cdot 310\,\mathrm {mm} \cdot 2\,\mathrm {mm} +2\cdot 25\,\mathrm {mm} \cdot 2\,\mathrm {mm} =16840\,\mathrm {mm^{2}} }$

Kantensumme: $K=4a+4b+4c=4(a+b+c)=4(310\,\mathrm {mm} +25\,\mathrm {mm} +2\,\mathrm {mm} )=1348\,\mathrm {mm}$

Umformen in der Raumgeometrie konkret

Bei manchen Aufgaben muss man die Formel umformen (wie bei der Geometrie der Ebene), z.B.:

Zylinder

Das Volumen eines (geraden) Zylinders ist 530cm³, seine Höhe 70mm. Wie viel ist seine Fläche?

In der Formelsammlung findet man die Formel für die Fläche:

Oberfläche: $A_{O}=2\pi \ r^{2}+2\pi \ r\ h$

Wenn man die Formel betrachtet, findet man schon das Symbol $h$ für die Höhe. Diese aber reicht nicht für die Berechnung des Volumens aus! Man braucht auch den Radius $r$ der Grundfläche. Daher wendet man sich an den anderen Vorgaben der Aufgabe. Dort findet man den Wert nicht nur für die Höhe, sondern auch fürs Volumen $V$.

Wir fangen mit der Formel die gegeben ist an.

Hier ist die Formel fürs Volumen gegeben:

$V=\pi r^{2}h$

Die Werte sowohl fürs Volumen als auch für die Höhe sind zwar gegeben, müssen allerdings übereinstimmen. Wir rechnen erst die 70 mm in cm um (siehe Kapitel „Einheiten umrechnen“): $h=70mm=7cm$

$\textstyle {\begin{aligned}V&=\pi r^{2}h&&\ \\530&=\pi \cdot r^{2}\cdot 7&&|:(7\pi )\\{\frac {530}{7\pi }}&=r^{2}&&\ \\24,1&\approx r^{2}&&|{\sqrt {\ \ }}\\r\approx {\sqrt {24,1}}&\approx 4,91\ cm\end{aligned}}$

Jetzt können wir leicht die Oberfläche berechnen, indem wir die entsprechende Formel anwenden:

$A_{O}=2\pi r(r+h)=2\pi \cdot 4,91\cdot (4,91+7)\approx 366,4\ cm^{2}$

Diagramme

Was ist ein Diagramm

In Diagrammen kann man verschiedene Daten in einem Bild darstellen, die man dann schnell ablesen kann. Diagramme können helfen, einen schnellen Überblick zu bekommen, werden aber auch oft benutzt, um einen falschen Eindruck zu bewirken. Hier werden das Säulendiagramm, das Liniendiagramm, das Kreisdiagramm und das Boxplotdiagramm präsentiert, es gibt aber auch zahlreiche andere Diagrammarten, wie z.B. Punktdiagramm, Balkendiagramm usw.

Säulendiagramm

Das Diagramm mit den Farben gibt die Anzahl der Steine in einem Kinderspiel, die eine gewisse Farbe haben. 4 Steine sind rot, 1 ist orange, 1 ist gelb, keine ist grün, es gibt 6 türkis usw. So ein Diagramm nennt man Säulendiagramm, weil es aus „Säulen“ besteht, wie in einem alten Tempel (Bild rechts). Die Farben sind sogenannte nominale Variablen. Nominale Variablen können wir zwar voneinander unterscheiden, wir können aber nicht z.B. sagen, dass rot "größer" als blau ist, wie z.B. wir sagen können, dass 4 mehr als 1 ist. Nominalen Variablen können wir also nicht der Größe nach ordnen. In diesem Diagramm können wir allerdings den sogenannten Modus ablesen, also welche Farbe am häufigsten vorkommt (Türkis).

Das folgende Diagramm gibt die Anzahl der Packungen, die eine gewisse Anzahl von Bananen pro Packung beinhalten. Die Anzahl der Bananen pro Packung ist eine sogenannte kardinale Größe (genauer gesagt: Variable einer Verhältnisskala). Wir können die einzelne Werte addieren, wir können auch dadurch einen Durchschnitt finden. Das geht allerdings nicht mit den Werten, die auf der x-Achse stehen (hier Bananen pro Packung), sondern nur mit den einzelnen Werten.

Säulendiagramm

Wenn die Frage z.B. ist, wie viele Packungen 4 Bananen haben, geht man so vor:

Auf der Achse unten (waagerechte Achse, x-Achse, auch Abszissenachse oder einfach Abszisse genannt) kann man die Bananen pro Packung ablesen, also kann man Bananen ablesen. Da wo 4 Bananen stehen (unten am Diagramm) befindet sich eine Säule. Man kann sehen, wie hoch diese Säule ist. Sie ist so hoch wie 5 Packungen. Die Anzahl der Packungen kann man links ablesen (auf der senkrechte Achse, der y-Achse, auch Ordinatenachse oder einfach Ordinate genannt). Also es gibt 5 Packungen mit 4 Bananen.

Wie viele Packungen haben 3 Bananen? Da, wo 3 Bananen stehen (unten, x-Achse), gibt es keine Säule! Die Höhe der Säule ist daher 0. Es gibt also keine (0) Packung, die 3 Bananen hat!

Wie viele Packungen haben keine Banane? Da, wo 0 Bananen stehen (unten, x-Achse), gibt es eine Säule, die 4 Packungen hoch ist. Es gibt also 4 Packungen mit keiner Banane!

Wie viele Packungen haben höchstens 3 Bananen? Höchstens bedeutet bis, also so viel wie 3 Bananen oder weniger (also 2, 1 oder keine Banane). Es gibt keine Packung mit 3 Bananen, 3 Pack. mit 2 Ban., 2 Pack. mit 1 Banane und 4 Pack. mit keiner Banane, also insgesamt 0+3+2+4=9 Pack..

Wie viele Packungen haben mindestens 3 Bananen? Mindestens bedeutet ab, also so viel wie 3 Bananen oder mehr (also 4, 5, 6 oder mehr Bananen). Es gibt keine Packung mit 3 Bananen, 5 Pack. mit 4 Ban. und 1 Pack. mit 5 Ban., also insgesamt 0+5+1=6 Pack..

Mittelwerte bei einem Säulendiagramm

Bei einem Säulendiagramm kann man auch Mittelwerte finden. Nehmen wir das gleiche Diagramm:

Aus dem Diagramm kann man eine Tabelle erzeugen!

	Bananen pro Packung	Anzahl der Packungen	Gesamte Bananen in diesen Packungen
	0	4	0⋅4=	0
	1	2	1⋅2=	2
	2	3	2⋅3=	6
	3	0	3⋅0=	0
	4	5	4⋅5=	20
	5	1	5⋅1=	5
		4+2+3+0+5+1=		0+2+6+0+20+5=
	Summe	15 Packungen		33 Bananen

Es gibt also 33 Bananen in 15 Packungen. Der Durchschnitt ist daher:  $\textstyle {\frac {33}{15}}=2,2$ B/P (Bananen pro Packung) im Durchschnitt.

Man kann auch den Median finden. Man soll die Werte (wie viele Bananen) einordnen. Wir haben 4 Packungen mit 0 Bananen (also die null kommt vier mal vor), 2 mit einer Banane, 3 mit 2 Bananen usw.:

$\underbrace {0,0,0,0,1,1,2,} _{\longleftarrow {\text{7 Werte}}}$  $\underbrace {2} _{Median}$  $\underbrace {,2,\overbrace {\color {Red}4,4,4,4,4} ^{Modus},5} _{{\text{7 Werte}}\longrightarrow }$

Wie man sehen kann, 3 kommt nicht vor. Wir haben ja keine Packung mit 3 Bananen, also der Wert 3 Bananen kommt nicht vor! Wir haben insgesamt 15 Werte (15 Packungen). Der Wert in der Mitte ist der achte Wert, also 2. Der Median ist 2.

Welcher Wert kommt öfters vor? 4 Bananen kommt 5 mal vor (in 5 Packungen). Alle andere Werte kommen nicht so oft vor. Also 4 ist der Modalwert.

Liniendiagramme

Lineare Funktion Diagramm

In einem Liniendiagramm spricht man von einem Koordinatensystem. Es gibt zwei „Koordinaten“, die x-Achse (senkrecht) und die y-Achse (waagerecht).

In Balkendiagramm im vorherigen Absatz hatten wir diskrete Werte. Das Wort „diskrete“ bedeutet in Mathematik, dass man z.B. den Wert 2 und den Wert 3 (Bananen im letzten Beispiel) hat, aber keinen Wert dazwischen (z.B. keine 2,156 Bananen). Das Gegenteil von diskreten Werten sind die kontinuierlichen Werte. In unserem Beispiel hier sieht man eine sogenannte (quasi-kontinuierliche) Kostenkurve. Man kann in Diagramm ablesen, sowohl wie viel die Produktion von z.B. 60 T-Shirts kostet, als auch wie viele T-Shirts man mit z.B. 20€ produzieren kann. Für die erste Frage (wie viel kosten 60 T-Shirts) fängt man an der x-Achse an, da wo die Anzahl der T-Shirts angegeben ist. Man geht von 60 (T-Shirts) senkrecht nach oben, bis man die Linie (oft Kurve genannt) trifft. Dann geht man waagerecht zur y-Achse (hier links), bis man die y-Achse trifft, da wo die Kosten stehen. In diesem Fall sind die Kosten 25€. Umgekehrt geht man vor, wenn die Kosten angegeben sind. In unserem Beispiel sind 20€ gegeben. Wie viele T-Shirts kann man damit produzieren? Man fängt in diesem Fall mit der y-Achse an, da auf dieser Achse die Kosten angegeben sind. Man geht dann waagerecht rechts bis man die Linie trifft und dann senkrecht nach unten, bis man die x-Achse trifft. Da kann man 45 T-Shirts ablesen. Man kann also mit 20€ 45 T-Shirts produzieren.

Liniendiagramm

Die Kurve in einem Liniendiagramm kann irgendeine Form haben (und nicht nur eine Gerade). Das folgende Beispiel zeigt die Körpertemperatur von einer Person (namens Gregor) am 12.3.15. Man kann sich aber vorstellen, was im Diagramm dargestellt wird. Man kann z.B. sehen welche Temperatur Gregor um 6 oder um 22.15 Uhr hatte, oder am welchen Zeitpunkten seine Temperatur z.B. 36,45°C oder 36,6°C war.