Endomorphismus, Automorphismus – Serlo „Mathe für Nicht-Freaks“

Ein Endomorphismus ist eine lineare Verformung eines Vektorraums $V$. Formal ist ein Endomorphismus eine lineare Abbildung $f$, die $V$ auf sich selbst abbildet, d.h. $f\colon V\to V$. Ein bijektiver Endomorphismus heißt Automorphismus. Intuitiv ist ein Automorphismus eine lineare Verformung, die man rückgängig machen kann.

Herleitung

Wir kennen schon lineare Abbildungen. Es sind diejenigen Abbildungen zwischen zwei Vektorräumen, welche sich mit der Struktur der Vektorräume vertragen. Wir untersuchen nun ein paar Beispiele von linearen Abbildungen, die wir schon in früheren Artikeln kennengelernt haben.

Beispiele im $\mathbb {R} ^{2}$

Streckung in $x$-Richtung

Zuerst betrachten wir die Streckung eines Vektors in der Ebene um den Faktor $2$ in $x$-Richtung. Unsere Abbildung ist damit

$f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},\ (x,y)\mapsto (2x,y).$

Man kann einfach nachprüfen, dass $f$ eine lineare Abbildung ist. Wir können $f$ wie folgt veranschaulichen: Wir legen ein Schachbrettmuster in die Ebene und wenden $f$ auf dieses Schachbrettmuster an.

Streckung der $x$-Achse um den Faktor $2$

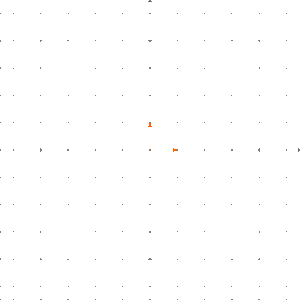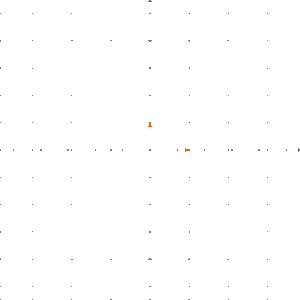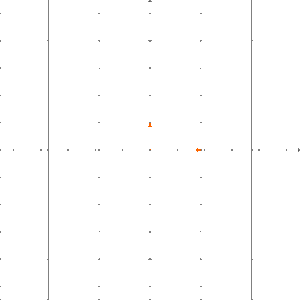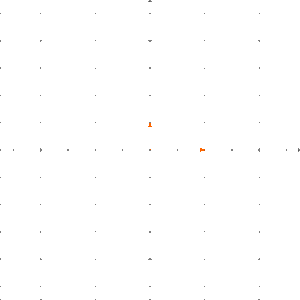
Das Ergebnis ist, dass die Boxen um den Faktor $2$ in $x$-Richtung gestreckt werden.

Drehung um den Ursprung

Wir betrachten nun eine Drehung $D_{\alpha }$ um den Winkel $\alpha$ gegen den Uhrzeigersinn mit dem Ursprung als Drehzentrum. Das ist eine Abbildung $D_{\alpha }:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$, die jedem Vektor $v\in \mathbb {R} ^{2}$ den um den Winkel $\alpha$ gedrehten Vektor $D_{\alpha }(v)\in \mathbb {R} ^{2}$ zuordnet:

Drehung eines Vektors $v\in \mathbb {R} ^{2}$ um den Winkel $\alpha$

Im Einführungsartikel zu linearen Abbildungen haben wir gesehen, dass Drehungen um den Ursprung linear sind. Wir können uns $D_{\alpha }$ wie im ersten Beispiel veranschaulichen, indem wir die Abbildung auf das Schachbrettmuster anwenden. Die einzelnen Felder bleiben dann gleich, sie werden nur gedreht.

Projektion auf eine Gerade

Anwendung von $P$ auf zwei Vektoren

Zuletzt betrachten wir die Abbildung

$P\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},\ (x,y)\mapsto (x,x).$

Die Abbildung $P$ „drückt“ Vektoren auf die Gerade $G=\{a\cdot (1,1)^{T}|a\in \mathbb {R} \}$. Man kann einfach nachrechnen, dass $P$ eine lineare Abbildung ist. Auch diese lineare Abbildung wenden wir auf das Schachbrettmuster an, um sie zu veranschaulichen.

Projektion auf die Diagonale in der Ebene

Das gesamte Gitter wird auf die Gerade $G$ „plattgedrückt“.

Lineare Verformungen eines beliebigen Vektorraums

In allen obigen Beispielen konnten wir die linearen Abbildungen als Verzerrungen des Schachbrettmusters im $\mathbb {R} ^{2}$ visualisieren. Das war möglich, weil alle obigen Funktionen vom $\mathbb {R} ^{2}$ wieder in den $\mathbb {R} ^{2}$ abbilden. Wir können beliebige lineare Abbildungen $\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ als Verformung des Schachbrettmusters veranschaulichen. Die Verformung des Schachbrettmusters zeigt uns, wie die Abbildung auf die Standardbasisvektoren $(1,0)^{T}$ und $(0,1)^{T}$ von $\mathbb {R} ^{2}$ und ganzzahlige Vielfache davon wirkt.

Jede lineare Abbildung $\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ ist eine lineare Verformung des Raums $\mathbb {R} ^{2}$. Diese Idee wollen wir auf allgemeine Vektorräume $V$ verallgemeinern. Wir können uns lineare Abbildungen von $V$ nach $V$ als lineare Verformungen bzw. Transformationen des Vektorraums $V$ vorstellen. Im Gegensatz dazu ist eine lineare Abbildung $V\to W$ ein Transport des Vektorraums $V$ nach $W$. Wir geben denjenigen linearen Abbildungen, die den Vektorraum verformen, d. h. die von $V$ nach $V$ abbilden, einen eigenen Namen. Wir nennen eine solche lineare Abbildung Endomorphismus. Also sind Endomorphismen genau die linearen Abbildungen, die den gleichen Definitions- und Zielbereich haben.

Rückgängig machbare Verformungen

In den Beispielen im $\mathbb {R} ^{2}$ haben wir gesehen, dass einige Verformungen den Raum erhalten und andere etwas platt drücken. Die Abbildungen, die den Raum erhalten, können wir rückgängig machen. Wenn etwas plattgedrückt wird, ist das nicht möglich, da Information verloren geht. Zum Beispiel geht bei der obigen linearen Abbildung „Projektion auf eine Gerade“ die Information verloren, welche $y$-Komponente der ursprüngliche Vektor hatte. Es ist nicht möglich, den Vektor nach Anwenden der Transformation wieder zurückzugewinnen. Es gibt also Verformungen des Raums, die man rückgängig machen kann, und welche, bei denen das nicht geht. Man kann eine Verformung genau dann rückgängig machen, wenn die dazugehörige Abbildung invertierbar ist. Das gibt uns die Definition einer rückgängig machbaren Verformung des Raums, d. h. ein invertierbarer Endomorphismus. Eine solche Abbildung heißt Automorphismus.

Definition

Definition (Endomorphismus und Automorphismus)

Sei $V$ ein $K$-Vektorraum. Eine lineare Abbildung $f\colon V\to V$, die $V$ auf sich selbst abbildet, heißt Endomorphismus. Die Menge aller Endomorphismen von $V$ bezeichnen wir mit $\operatorname {End} _{K}(V)$.

Einen bijektiven Endomorphismus nennen wir Automorphismus. Die Menge aller Automorphismen von $V$ wird mit $\operatorname {Aut} _{K}(V)$ bezeichnet.

Hinweis

Jeder Automorphismus ist eine bijektive lineare Abbildung und damit auch ein Isomorphismus. Aber nicht jeder Isomorphismus ist ein Automorphismus. Denn Isomorphismen können auch zwei verschiedene Vektorräume aufeinander abbilden.

Beispiele

Beispiele im $\mathbb {R} ^{2}$

Spiegelung

Wir betrachten die lineare Abbildung $f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},(x,y)^{T}\mapsto (-x,y)^{T}$. Da sie als Definitions- sowie als Bildraum den gleichen Vektorraum $\mathbb {R} ^{2}$ hat, ist sie ein Endomorphismus. Die Abbildung $f$ hält $y$ fest und schickt $x$ auf $-x$. Damit können wir uns $f$ als eine Spiegelung entlang der $y$-Achse vorstellen. Eine Spiegelung können wir rückgängig machen, indem wir ein zweites Mal spiegeln. Das bedeutet, dass $f$ selber die zu $f$ inverse Abbildung $f$ ist. Formal heißt das $f\circ f=\operatorname {id} _{\mathbb {R} ^{2}}$ bzw. $f^{-1}=f$. Eine solche Abbildung nennt man auch „selbstinvers.“ Weil $f$ ein Inverses besitzt, also invertierbar ist, folgt, dass $f$ bijektiv ist. Somit ist $f$ auch ein Automorphismus.

Drehung um 90°

Als nächstes betrachten wir den Endomorphismus $f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},(x,y)^{T}\mapsto (-y,x)^{T}$. Wir wollen zunächst sehen, dass es sich hierbei um eine Drehung um $90$ Grad gegen den Uhrzeigersinn handelt. Dazu genügt es zu berechnen, dass $f$ auf den Standardbasisvektoren $(1,0)^{T}$ und $(0,1)^{T}$ wie eine solche Drehung wirkt, da wegen der Linearität daraus folgt, dass $f$ dann insgesamt eine solche Drehung sein muss. Wir berechnen $f((1,0)^{T})=(0,1)^{T}$, sowie $f((0,1)^{T})=(-1,0)^{T}$, und sehen, dass es sich um die gewünscht Drehung handelt. Auch hier können wir leicht ein Inverses angeben, indem wir „zurückdrehen“ bzw. um $90$ Grad im Uhrzeigersinn drehen. Diese Drehung ist durch $g\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},(x,y)^{T}\mapsto (y,-x)^{T}$ gegeben. Wir rechnen kurz nach, dass $g$ tatsächlich die Inverse von $f$ ist: Es gilt

${\begin{aligned}(f\circ g){\begin{pmatrix}x\\y\end{pmatrix}}&=f{\begin{pmatrix}y\\-x\end{pmatrix}}={\begin{pmatrix}-(-x)\\y\end{pmatrix}}={\begin{pmatrix}x\\y\end{pmatrix}}{\text{, sowie }}\\[0.5em](g\circ f){\begin{pmatrix}x\\y\end{pmatrix}}&=g{\begin{pmatrix}-y\\x\end{pmatrix}}={\begin{pmatrix}x\\-(-y)\end{pmatrix}}={\begin{pmatrix}x\\y\end{pmatrix}}\end{aligned}}$

für $(x,y)^{T}\in \mathbb {R} ^{2}$. Also gilt $f\circ g=\operatorname {id} _{\mathbb {R} ^{2}}=g\circ f$ und $f$ ist auch in diesem Beispiel ein Automorphismus.

Scherung

Sei $f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},(x,y)^{T}\mapsto (x+2y,y)^{T}$. Wie diese Abbildung den Raum verformt, können wir in der Animation sehen.

Scherung der Ebene

Die Transformation sieht umkehrbar aus, d.h. sie sieht aus als wäre sie ein Automorphismus. Das können wir überprüfen, indem wir zeigen, dass $f$ injektiv und surjektiv ist.

Um die Injektivität zu zeigen, gucken wir uns den Kern von $f$ an, d. h. $\{(x,y)^{T}\in \mathbb {R} ^{2}\mid f((x,y)^{T})=(0,0)^{T}\}$. Für einen Vektor $(x,y)^{T}$ im Kern, gilt dann $(x+2y,y)^{T}=(0,0)^{T}$. Daraus folgt direkt $y=0$ und damit auch $x=x+2y=0$. Somit besteht der Kern nur aus dem Nullvektor und damit ist $f$ injektiv.

Um die Surjektivität zu zeigen, nehmen wir uns ein beliebiges $(x',y')^{T}\in \mathbb {R} ^{2}$ und finden ein passendes Urbild unter $f$. Wir suchen also $(x,y)^{T}\in \mathbb {R} ^{2}$ mit $(x+2y,y)^{T}=f((x,y)^{T})=(x',y')^{T}$. Es ist direkt klar, dass $y=y'$ sein muss. Weiterhin muss $x+2y=x+2y'=x'$ gelten. Das lässt sich zu $x=(x'-2y')^{T}$ umformen. Also ist $(x'-2y',y')^{T}$ ein Urbild von $(x',y')^{T}$. Da $(x',y')^{T}$ beliebig waren, ist $f$ surjektiv.

Abbildungen der Form $f((x,y)^{T})=(x+\lambda y,y)^{T}$ mit $\lambda \in K$ heißen Scherungen. Du kannst als Übunsaufgabe zeigen, dass eine Scherung immer ein Automorphismus ist, egal was für eine Zahl $\lambda$ ist.

Plattdrücken auf die $x$-Achse

Betrachten wir nun die Abbildung $f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},(x,y)^{T}\mapsto (x+y,0)^{T}$. Diese ist ein Endomorphismus von $\mathbb {R} ^{2}$ auf $\mathbb {R} ^{2}$, der jeden Punkt auf der Ebene auf einen Punkt auf der $x$-Achse abbildet. Wir können uns also vorstellen, dass $f$ die 2-dimensionale Ebene auf die $x$-Achse „plattgedrückt.“

Da $f$ die Punkte in $\mathbb {R} ^{2}$ ausschließlich auf die $x$-Achse abbildet, ist $f$ keine surjektive Abbildung. Injektiv ist sie auch nicht, denn für jedes $z\in \mathbb {R}$ können wir unterschiedliche $x,y\in \mathbb {R}$ finden, sodass $x+y=z$ gilt, z.B. $x=z,y=0$ und umgekehrt. Also ist $f$ kein Automorphismus.

Plattdrücken auf die x-Achse

Beispiel im $\mathbb {R} ^{3}$

Betrachten wir nun ein Beispiel im $\mathbb {R} ^{3}$. Wir sehen uns dafür die lineare Abbildung $f\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3},(x,y,z)^{T}\mapsto (x+y,x+y,z)^{T}$ an. Weil $f$ den Vektorraum $\mathbb {R} ^{3}$ wieder nach $\mathbb {R} ^{3}$ abbildet, ist die Abbildung ein Endomorphismus.

Wir wollen nun prüfen, ob $f$ auch ein Automorphismus ist. Dafür müssen wir die Surjektivität und Injektivität überprüfen. Für die Injektivität betrachten wir den Kern von $f$, also $\{(x,y,z)^{T}\in \mathbb {R} ^{3}|f((x,y,z)^{T})=(0,0,0)^{T}\}$. Für Vektoren $(x,y,z)^{T}$ aus dem Kern von $f$ gilt also $(x+y,x+y,z)^{T}=(0,0,0)^{T}$. Daraus können wir direkt schließen, dass $z=0$ und $x+y=0$, also $y=-x$, gelten muss. Wir sehen damit, dass der Kern von $f$ nicht nur den Nullvektor enthält, sondern auch die Menge aller Vektoren $\{(x,-x,0)^{T}|x\in \mathbb {R} \}$. Somit ist $f$ nicht injektiv und kann daher auch nicht bijektiv sein. Insbesondere ist $f$ kein Automorphismus.

Anschaulich drückt $f$ Vektoren auf die Ebene $\{(x,x,z)^{T}\mid x,z\in \mathbb {R} \}$ zusammen. Es gehen somit Informationen verloren. Wenn man einen Vektor $(x,x,z)^{T}\in \mathbb {R} ^{3}$ hat, kann man nicht mehr auf eindeutige Weise sagen, aus welchem Vektor $(a,b,z)^{T}\in \mathbb {R} ^{3}$ er unter der Abbildung $f$ entstanden ist, da es sehr viele Wege gibt, $x\in \mathbb {R}$ als Summe zweier Zahlen $a,b\in \mathbb {R}$ darzustellen. Beispielsweise gilt $5=2+3=1+4=-1000+1005$.

Beispiel im Folgenraum

Es gibt auch Endomorphismen auf anderen Vektorräumen als $\mathbb {R} ^{2}$ und $\mathbb {R} ^{3}$. Für einen beliebigen Körper $K$ betrachten wir den Folgenraum

$\omega :=\{(x_{i})_{i}\mid x_{i}\in K{\text{ für alle }}i\in \mathbb {N} \}.$

Wir betrachten die Abbildung

${\begin{aligned}f\colon \omega &\to \omega \\[0.3em](x_{i})_{i}&\mapsto f\left((x_{i})_{i}\right)=(x_{k(i)})_{i},\end{aligned}}$

wobei

$k(i)={\begin{cases}i-1&{\text{falls }}i{\text{ gerade ist}}\\i+1&{\text{falls }}i{\text{ ungerade ist}}.\end{cases}}$

Wenn wir die ersten Folgenglieder ausschreiben, sieht die Abbildung so aus:

$f(x_{1},x_{2},x_{3},x_{4},\ldots )=(x_{2},x_{1},x_{4},x_{3},\ldots ).$

Die Abbildung $f$ vertauscht also gerade und ungerade Folgenglieder miteinander. Wir begründen kurz, warum $f$ linear ist. Die Addition und skalare Multiplikation im Folgenraum ist komponentenweise, d.h. für $(x_{i})_{i}$ und $(y_{i})_{i}\in \omega$ und $\lambda \in K$ gilt

$(x_{i})_{i}+(y_{i})_{i}=(x_{i}+y_{i})_{i}{\text{ und }}\lambda \cdot (x_{i})_{i}=(\lambda \cdot x_{i})_{i}.$

Da $f$ nur die Reihenfolge der Komponenten vertauscht, ist $f$ linear. Wir können von $f$ auch explizit nachprüfen.

Frage: Wie zeigt man direkt, dass $f$ linear ist?

Wir beweisen Additivität und Homogenität von $f$. Seien $(x_{i})_{i}$ und $(y_{i})_{i}\in \omega$ und $\lambda \in K$. Dann ist

${\begin{aligned}&f((x_{i})_{i}+(y_{i})_{i})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Addition von Folgen}}\right.}\\[0.3em]=&f((x_{i}+y_{i})_{i})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f\right.}\\[0.3em]=&(x_{k(i)}+y_{k(i)})_{i}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Addition von Folgen}}\right.}\\[0.3em]=&(x_{k(i)})_{i}+(y_{k(i)})_{i}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f\right.}\\[0.3em]=&f((x_{i})_{i})+f((y_{i})_{i})\end{aligned}}$

und

${\begin{aligned}&f(\lambda \cdot (x_{i})_{i})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Skalare Multiplikation von Folgen}}\right.}\\[0.3em]=&f((\lambda \cdot x_{i})_{i})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f\right.}\\[0.3em]=&(\lambda \cdot x_{k(i)})_{i}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Skalare Multiplikation von Folgen}}\right.}\\[0.3em]=&\lambda \cdot (x_{k(i)})_{i})_{i}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f\right.}\\[0.3em]=&\lambda \cdot f((x_{i})_{i}).\end{aligned}}$

Also ist $f$ ein Endomorphismus von $\omega$. Ist $f$ auch ein Automorphismus? Um das zu beantworten, müssen wir überprüfen, ob man $f$ rückgängig machen kann. Die Abbildung vertauscht gerade und ungerade Folgenglieder miteinander. Wenn wir die Folgenglieder wieder zurücktauschen, ist $f$ wieder rückgängig gemacht. Beim Zurücktauschen werden wieder gerade und ungerade Folgenglieder vertauscht, d.h. das Zurücktauschen ist wieder $f$. Wie beim allerersten Beispiel ist $f$ selbstinvers – in Formeln heißt das $f\circ f=\operatorname {id} _{\omega }$ bzw. $f=f^{-1}$. Da $f$ invertierbar ist, ist die Abbildung bijektiv. Also ist $f$ ein Automorphismus.

Endomorphismen bilden einen Ring mit Eins

Im Artikel Vektorraum linearer Abbildungen haben wir gesehen, dass die Menge der linearen Abbildungen $\operatorname {Hom} _{K}(V,W)$ zwischen zwei $K$-Vektorräumen $V$ und $W$ wieder einen Vektorraum bildet. Da $\operatorname {End} _{K}(V)=\operatorname {Hom} _{K}(V,V)$ gilt, ist auch die Menge Endomorphismen ein Vektorraum. Das heißt, wir können Endomorphismen eines Vektorraums $V$ addieren und mit Skalaren multiplizieren. Insbesondere können wir zwei Endomorphismen $f$ und $g\in \operatorname {End} _{K}(V)$ durch Addition verknüpfen und erhalten einen Endomorphismus $f+g\in \operatorname {End} _{K}(V)$. Dieser ist durch

$f+g:V\to V,\quad (f+g)(v):=f(v)+_{V}g(v)$

definiert, wobei $+_{V}$ die Addition im Vektorraum $V$ bezeichnet.

Lassen sich $f$ und $g$ auch auf eine andere Art verknüpfen? Intuitiv sind $f$ und $g$ zwei Verfomungen des Vektorraums $V$. Wir können nun mit $f$ den Raum $V$ verformen und anschließend das Ergebnis mit $g$ verformen. Dabei kommt eine neue Verformung des Vektorraums heraus. Das heißt, wir erhalten wieder einen Endomorphismus von $V$. Diese Abbildung, die aus dem Hintereinanderausführen vom $f$ und $g$ entsteht, ist die Komposition $g\circ f$. Die Komposition von zwei Endomorphismen ist also immer ein Endomorphismus. Zusammengefasst können wir zwei Endomorphismen $f$ und $g$ verknüpfen, indem wir die Addition $f+g$ oder die Komposition $g\circ f$ bilden.

Weil wir neben er Addition auch die Komposition als Verknüpfung haben, trägt $\operatorname {End} _{K}(V)$ mehr Struktur als nur die Vektorraumstruktur. Wir werden später beweisen, dass die Menge $\operatorname {End} _{K}(V)$ der Endomorphismen auf $V$ mit diesen Verknüpfungen einen Ring bildet. Die Addition im Ring ist dabei die Addition der Abbildungen und die Multiplikation im Ring ist die Komposition der Abbildungen.

Wir überlegen uns nun, ob der Ring $\operatorname {End} _{K}(V)$ eine Eins hat und kommutativ ist. Eine Eins existiert, wenn es ein neutrales Element der Multiplikation gibt. Das heißt, wenn es ein $k\in \operatorname {End} _{K}(V)$ gibt, so dass $k\circ f=f$ und $f\circ k=f$ für alle $f\in \operatorname {End} _{K}(V)$ gilt. Wir kennen schon eine Abbildung, die diese Eigenschaft erfüllt: die Identität $\operatorname {id} _{V}$. Das ist eine lineare Abbildung $V\to V$ und damit gilt $\operatorname {id} _{V}\in \operatorname {End} _{K}(V)$. Also hat der Ring $\operatorname {End} _{K}(V)$ eine Eins.

Ist $\operatorname {End} _{K}(V)$ ein kommutativer Ring? Um das zu beantworten, müssen wir prüfen, ob $f\circ g=g\circ f$ für alle $f,g\in \operatorname {End} _{K}(V)$ gilt. Wir überlegen uns das wieder mit Beispielen über $\mathbb {R} ^{2}$. Sei $f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2}$ die Projektion auf die $y$-Achse; das heißt, für $(x,y)\in \mathbb {R} ^{2}$ gilt $f(x,y)=(0,y)$. Außerdem sei $g\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2}$ die Drehung um $90^{\circ }$ im Urzeigersinn (bzw. um $270^{\circ }$ gegen den Uhrzeigersinn) um den Ursprung; das heißt, es gilt $g(x,y)=(-y,x)$. Wir wollen untersuchen, ob $f\circ g=g\circ f$ gilt. Was machen die Abbildungen $f\circ g$ und $g\circ f$ anschaulich? Die Abbildung $g\circ f$ drückt erst den ganzen Raum auf die $y$-Achse und dreht diese anschließend um $90^{\circ }$ im Urzeigersinn. Unser Ergebnis liegt also auf der $x$-Achse.

$g\circ f$

Die Abbildung $f\circ g$ dreht zuerst den Raum um $90^{\circ }$ im Urzeigersinn und drückt anschließend alles auf die $y$-Achse. Also liegt das Ergebnis der Abbildung auf der $y$-Achse.

$f\circ g$

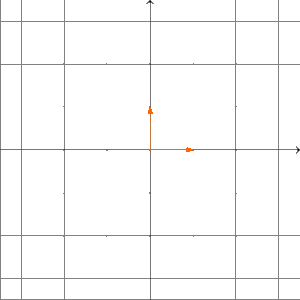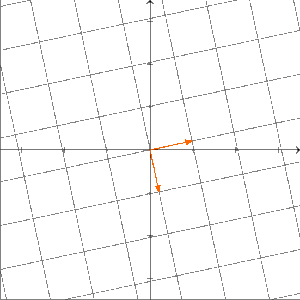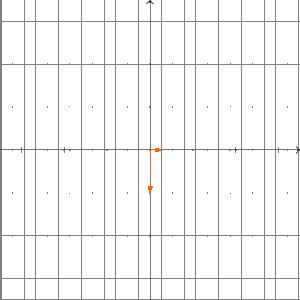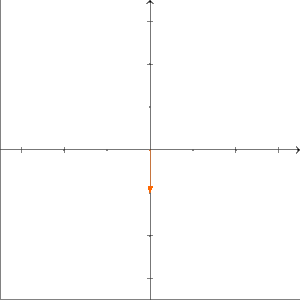
Folglich sind $f\circ g$ und $g\circ f$ verschiedene Abbildungen. Deshalb ist $\operatorname {End} _{\mathbb {R} }(\mathbb {R} ^{2})$ kein kommutativer Ring. Allgemeiner gilt: Für jeden Vektorraum $V$ mit $\dim V\geq 2$ ist $\operatorname {End} _{K}(V)$ kein kommutativer Ring. Das behandeln wir unten in einer Aufgabe.

Wie oben angekündigt beweisen wir jetzt, dass $(\operatorname {End} _{K}(V),+,\circ )$ ein Ring ist:

Satz (Endomorphismenring)

Sei $K$ ein Körper und $V$ ein $K$-Vektorraum. Dann bildet die Menge der Endomorphismen $\operatorname {End} _{K}(V):=\{f\colon V\to V\mid f{\text{ ist linear}}\}$ von $V$ zusammen mit Addition $+$ und Komposition $\circ$ einen Ring mit Eins.

Für zwei Endomorphismen $f,g\in \operatorname {End} _{K}(V)$ sind $f+g\colon V\to V$ und $f\circ g\colon V\to V$ durch

$(f+g)(v):=f(v)+_{V}g(v)$ und $(f\circ g)(v):=f(g(v))$ für $v\in V$

definiert. Hierbei ist $+_{V}$ die Addition von $V$.

Beweis (Endomorphismenring)

Damit $(\operatorname {End} _{K}(V),+,\circ )$ einen Ring mit Eins bildet, müssen folgende Eigenschaften erfüllt sein:

• Das Tupel ($\operatorname {End} _{K}(V),+$) ist eine abelsche Gruppe.
  1. Assoziativgesetz der Addition: $\forall f,g,h\in \operatorname {End} _{K}(V):\ f+(g+h)=(f+g)+h$
  2. Kommutativgesetz der Addition: $\forall f,g\in \operatorname {End} _{K}(V):\ f+g=g+f$
  3. Existenz eines additiven neutralen Elements: $\exists e\in \operatorname {End} _{K}(V)\;\forall f\in {\operatorname {End} _{K}(V)}:\ e+f=f$
  4. Existenz von additiven Inversen: $\forall f\in \operatorname {End} _{K}(V)\;\exists f'\in \operatorname {End} _{K}(V):\ f'+f=e$
• Das Tupel ($\operatorname {End} _{K}(V),\circ$) ist ein Monoid
  1. Assoziativgesetz der Multiplikation: $\forall f,g,h\in \operatorname {End} _{K}(V):\ f\circ (g\circ h)=(f\circ g)\circ h$
  2. Existenz eines multiplikativen neutralen Elements: $\exists k\in \operatorname {End} _{K}(V)\;\forall f\in \operatorname {End} _{K}(V):\ k\circ f=f$
• Es gelten die Distributivgesetze
  1. Distributivgesetz I: $\forall f,g,h\in \operatorname {End} _{K}(V):\ f\circ (g+h)=f\circ g+f\circ h$
  2. Distributivgesetz II: $\forall f,g,h\in \operatorname {End} _{K}(V):\ (f+g)\circ h=f\circ h+g\circ h$

Bevor wir mit dem Beweis starten, wollen wir folgende einfache Tatsache im Hinterkopf behalten:

Seien $f,g,h\in \operatorname {End} K(V)$ und $x\in V$. Die Abbildungen $f,g$ und $h$ bilden Elemente von $V$ auf Elemente von $V$ ab. Dementsprechend sind $f(x),g(x),h(x)$ Elemente von $V$. Nach Voraussetzung ist $(V,+_{V},\cdot _{V})$ ein $K$-Vektorraum. Deshalb können wir die Rechenregeln, die im $K$-Vektorraum gelten, auch auf die Elemente $f(x),g(x),h(x)$ anwenden.

Beweisschritt: ($\operatorname {End} _{K}(V),+$) ist eine abelsche Gruppe

Beweisschritt: Assoziativgesetz der Addition

Das Assoziativgesetz der Addition lautet: $\forall f,g,h\in \operatorname {End} _{K}(V):\ f+(g+h)=(f+g)+h$

Diese Gleichung beweisen wir, indem wir für alle $f,g,h\in \operatorname {End} _{K}(V)$ die Gleichung $(f+(g+h))(x)=((f+g)+h)(x)$ für jeden Vektor $x\in V$ beweisen.

Seien daher $f,g,h\in \operatorname {End} K(V)$ und $x\in V$. Dann gilt

${\begin{aligned}&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]((f+g)+h)(x)&=(f+g)(x)+_{V}h(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(f(x)+_{V}g(x))+_{V}h(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Assoziativität der Addition in }}V\right.}\\[0.3em]&=f(x)+_{V}(g(x)+_{V}h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=f(x)+_{V}(g+h)(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(f+(g+h))(x)\\[0.3em]\end{aligned}}$

Damit ist die Assoziativität gezeigt.

Beweisschritt: Kommutativgesetz der Addition

Das Kommutativgesetz der Addition lautet: $\forall f,g\in \operatorname {End} _{K}(V):\ f+g=g+h$ Diese Gleichung beweisen wir, in dem wir für alle $f,g\in \operatorname {End} _{K}(V)$ die Gleichung $(f+g)(x)=(g+f)(x)$ für jedes $x\in V$ beweisen.

Seien daher $f,g\in \operatorname {End} K(V)$ und $x\in V$. Dann gilt

${\begin{aligned}&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em](f+g)(x)&=f(x)+_{V}g(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Kommutativität der Addition in }}V\right.}\\[0.3em]&=g(x)+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(g+f)(x)\\[0.3em]\end{aligned}}$

Damit ist die Kommutativität gezeigt.

Beweisschritt: Existenz eines additiven neutralen Elements

Wir müssen folgende Aussage zeigen: $\exists e\in \operatorname {End} _{K}(V)\;\forall f\in {\operatorname {End} _{K}(V)}:\ e+f=f$

Diese Aussage beweisen wir, in dem wir folgende Aussage zeigen: $\exists e\in \operatorname {End} _{K}(V)\;\forall f\in {\operatorname {End} _{K}(V)}:\ (e+f)(x)=f(x)\quad x\in V$

Wir wählen $e=0_{\operatorname {Abb(V,V)} }\in \operatorname {End} K(V)\subseteq Abb(V,V)$, wobei $0_{\operatorname {Abb(V,V)} }:V\rightarrow V,x\mapsto 0_{V}$ die Nullabbildung von $V$ nach $V$ ist. Wir zeigen nun, dass $0_{\operatorname {Abb(V,V)} }$ das neutrale Element der Addition ist. Seien dafür $f\in \operatorname {End} K(V)$ und $x\in V$. Dann gilt

${\begin{aligned}&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em](0_{\operatorname {Abb(V,V)} }+f)(x)&=0_{\operatorname {Abb(V,V)} }(x)+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}0_{\operatorname {Abb(V,V)} }\right.}\\[0.3em]&=0_{V}+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Neutrales Element der Addition in }}V\right.}\\[0.3em]&=f(x)\\[0.3em]\end{aligned}}$

Das additive neutrale Element ist hier also die Nullabbildung $0_{\operatorname {Abb(V,V)} }:V\rightarrow V,x\mapsto 0_{V}$.

Beweisschritt: Existenz von additiven Inversen

Wir müssen folgende Aussage zeigen: $\forall f\in \operatorname {End} K(V)\;\exists f'\in \operatorname {End} _{K}(V):\ f'+f=0_{\operatorname {Abb(V,V)} }$

Diese Aussage beweisen wir, in dem wir folgende Aussage zeigen: $\forall f\in \operatorname {End} K(V)\;\exists f'\in \operatorname {End} _{K}(V)\;\forall x\in V:\ (f'+f)(x)=0_{V}=0_{\operatorname {Abb(V,V)} }(x)$

Da $V$ ein $K$-Vektorraum ist, hat ein beliebiger Vektor $v\in V$ ein additive Inverse, nämlich $-v$. Es gilt dann $v+_{V}(-v)=0_{V}$. Wir können daher für einen beliebigen Endomorphismus $f\in \operatorname {End} _{K}(V)$ einfach $f':V\rightarrow V,x\mapsto -f(x)$ wählen. Das müssen wir nun noch zeigen. Seien dafür $f\in \operatorname {End} K(V)$ und $x\in V$. Dann gilt

${\begin{aligned}&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em](f'+f)(x)&=f'(x)+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f'\right.}\\[0.3em]&=-f(x)+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{additive Inverse in }}V\right.}\\[0.3em]&=0_{V}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}0_{\operatorname {Abb(V,V)} }\right.}\\[0.3em]&=0_{\operatorname {Abb(V,V)} }(x)\\[0.3em]\end{aligned}}$

Also ist die additive Inverse einer Abbildung $f:V\rightarrow V,x\mapsto f(x)$ die Abbildung $f':V\rightarrow V,x\mapsto -f(x)$.

Wir haben damit bewiesen, dass $(\operatorname {End} _{K}(V),+)$ eine abelsche Gruppe ist.

Diese Aussage hätten wir auch anders zeigen können. Im Artikel Vektorraum linearer Abbildungen haben wir die Menge der linearen Abbildungen zwischen zwei $K$-Vektorräumen $V$ und $W$ betrachtet. Diese Menge nennen wir $\operatorname {Hom} (V,W)$. Wir haben gesehen, dass $\operatorname {Hom} (V,W)$ einen $K$-Vektorraum bildet. Es gilt $\operatorname {End} _{K}(V)=\operatorname {Hom} (V,V)$. Also ist auch $\operatorname {End} _{K}(V)$ ein Vektorraum und damit eine abelsche Gruppe.

Beweisschritt: ($\operatorname {End} _{K}(V),\circ$) ist ein Monoid

Beweisschritt: Assoziativgesetz der Multiplikation

Das Assoziativgesetz der Multiplikation in $\operatorname {End} _{K}(V)$ lautet: $\forall f,g,h\in \operatorname {End} _{K}(V):\ f\circ (g\circ h)=(f\circ g)\circ h$

Das gilt, da die Komposition von Abbildungen assoziativ ist.

Beweisschritt: Existenz eines multiplikativen neutralen Elements

Wir müssen folgende Aussage zeigen: $\exists k\in \operatorname {End} _{K}(V)\;\forall f\in {\operatorname {End} _{K}(V)}:\ k\circ f=f$

Diese Aussage beweisen wir, in dem wir folgende Aussage zeigen: $\exists k\in \operatorname {End} _{K}(V)\;\forall f\in {\operatorname {End} _{K}(V)}\;\forall x\in V:\ (k\circ f)(x)=f(x)$

Wir wählen $k=\operatorname {id} _{V}\in \operatorname {End} K(V)\subseteq Abb(V,V)$, wobei $\operatorname {id} _{V}:V\rightarrow V,\ x\mapsto x$ die Identität auf $V$ ist. Wir wollen noch zeigen, dass $k$ das neutrale Element der Multiplikation ist. Seien dafür $f\in \operatorname {End} K(V)$ und $x\in V$. Dann gilt

${\begin{aligned}&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}k\right.}\\[0.3em](k\circ f)(x)&=(\operatorname {id} _{V}\circ f)(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}\circ \right.}\\[0.3em]&=\operatorname {id} _{V}(f(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}\operatorname {id} _{V}\right.}\\[0.3em]&=f(x)\\[0.3em]\end{aligned}}$

Also ist das neutrale Element der Multiplikation in gegeben durch die Identität auf $V$, d.h. $\operatorname {id} _{V}:V\to V,\ x\mapsto x$.

Beweisschritt: Distributivgesetze

Beweisschritt: Distributivgesetz I

Das Distributivgesetz I lautet: $\forall f,g,h\in \operatorname {End} _{K}(V):\ f\circ (g+h)=f\circ g+f\circ h$

Diese Gleichung beweisen wir, indem wir für alle $f,g,h\in \operatorname {End} _{K}(V)$ die Gleichung $(f\circ (g+h))(x)=(f\circ g+f\circ h)(x)$ für jedes $x\in V$ zeigen. Seien $f,g,h\in \operatorname {End} K(V)$ und $x\in V$. Dann gilt

${\begin{aligned}&{\color {OliveGreen}\left\downarrow \ {\text{Definition der Komposition}}\right.}\\[0.3em](f\circ (g+h))(x)&=f((g+h)(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=f(g(x)+_{V}h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{f ist linear}}\right.}\\[0.3em]&=f(g(x))+_{V}f(h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition der Komposition}}\right.}\\[0.3em]&=(f\circ g)(x)+_{V}(f\circ h)(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(f\circ g+f\circ h)(x)\end{aligned}}$

Damit ist die Distributivität I gezeigt.

Beweisschritt: Distributivgesetz II

Das Distributivgesetz II lautet: $\forall f,g,h\in \operatorname {End} _{K}(V):\ (f+g)\circ h=f\circ h+g\circ h$

Diese Gleichung beweisen wir, in dem wir die Gleichung $((f+g)\circ h)(x)=(f\circ h+g\circ h)(x)$ für alle $f,g,h\in \operatorname {End} _{K}(V)$ und $x\in V$ zeigen. Seien dafür $f,g,h\in \operatorname {End} K(V)$ und $x\in V$. Dann gilt

${\begin{aligned}&{\color {OliveGreen}\left\downarrow \ {\text{Definition der Komposition}}\right.}\\[0.3em]((f+g)\circ h)(x)&=(f+g)(h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=f(h(x))+_{V}g(h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition der Komposition }}\right.}\\[0.3em]&=(f\circ h)(x)+_{V}(g\circ h)(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(f\circ h+g\circ h)(x)\end{aligned}}$

Damit ist die Distributivität II gezeigt.

Automorphismen und platt drücken

Der endlichdimensionale Fall

Oben haben wir bereits einige Beispiele von Endo- und Automorphismen untersucht. Dabei haben wir gesehen, dass Endomorphismen, die etwas „plattdrücken“, nicht bijektiv und damit keine Automorphismen sind. Andererseits waren Endomorphismen, die nichts „plattdrücken“, schon Automorphismen.

Frage: Was ist „nichts plattdrücken“ in mathematischer Sprache?

Ein Endomorphismus $f\colon V\to V$ „drückt nichts platt“, wenn es keinen Vektor $v\neq 0$ gibt, der von $f$ auf Null abgebildet wird. Das heißt, für alle Vektoren $v\neq 0$, gilt $f(v)\neq 0$. Da $f$ eine lineare Abbildung ist, gilt das genau dann, wenn $f$ injektiv, also ein Monomorphismus ist.

Bei Endomorphismen von endlich-dimensionalen Vektorräumen ist „nichts plattdrücken“ gleichbedeutend mit „Automorphismus sein“: Sei $f\colon V\to V$ ein Endomorphismus eines $n$-dimensionalen Vektorraums $V$. Wenn die Abbildung $f$ ein Automorphismus ist, ist sie insbesondere injektiv. Also drückt $f$ nichts in $V$ platt. Wenn wir umgekehrt annehmen, dass $f$ nichts plattdrückt, folgt, dass $f$ injektiv ist. Damit gehen keine Informationen aus $V$ beim Abbilden mit $f$ verloren. Daraus können wir schließen, dass das Bild $\operatorname {im} (f)=f(V)$ auch $n$-dimensional ist. Also muss $\operatorname {im} (f)=V$ gelten. Damit ist $f$ auch surjektiv und somit ein Automorphismus.

Wir haben gesehen, dass ein injektiver Endomorphismus über einen endlich-dimensionalen Vektorraum automatisch surjektiv ist. Gilt auch die umgekehrte Aussage? In anderen Worten: Wenn $f\colon V\to V$ ein surjektiver Endomorphismus eines $n$-dimensionalen Vektorraums ist, folgt dann, dass $f$ injektiv ist? Wenn $f$ surjektiv ist, gilt $f(V)=V$ und damit $\dim(f(V))=n$. Angenommen $f$ ist nicht injektiv. Dann gibt es einen Vektor $0\neq v\in V$ für den $f(v)=0$ gilt. Dann drückt $f$ die Richtung platt, in die $v$ zeigt. Das bedeutet, beim Abbilden von $V$ durch $f$ verlieren wir mindestens eine Dimension von $V$. Folglich wäre dann $\dim(f(V))<n$. Das ist ein Widerspruch zu $\dim(f(V))=n$. Deshalb muss $f$ injektiv sein. Also gilt, wenn $f$ surjektiv ist, dann ist $f$ auch injektiv.

To-Do:

evtl. verweisen auf eine Erklärung im Artikel "Lineare Abbildungen zwischen endlichdimensionalen Vektorräumen", wenn dieser geschrieben ist.

Diese Aussagen zeigen wir in folgendem Satz noch einmal formal.

Satz (Endomorphismen auf endlichdimensionalen Vektorräumen)

Sei $V$ ein endlichdimensionaler Vektorraum und $f\colon V\to V$ ein Endomorphismus. Dann ist äquivalent

• $f$ ist ein Isomorphismus
• $f$ ist ein Monomorphismus
• $f$ ist ein Epimorphismus

Beweis (Endomorphismen auf endlichdimensionalen Vektorräumen)

Wir wissen schon, dass für zwei endlich-dimensionale Vektorräume $V$ und $W$ mit $\dim V=\dim W$ und eine lineare Abbildung $f\colon V\to W$ gilt, dass die Aussagen

• $f$ ist ein Isomorphismus
• $f$ ist ein Monomorphismus
• $f$ ist ein Epimorphismus

äquivalent sind. Also folgt für einen Endomorphismus $f\colon V\to V$ von einem endlich-dimensionalen Vektorraum $V$, dass die drei Aussagen äquivalent sind.

To-Do:

Den Satz für allgemeine lineare Abbildungen verlinken, sobald er geschrieben wurde

Der unendlichdimensionale Fall

Im Unendlichdimensionalen funktioniert das obige Argument nicht mehr. Wir haben im endlichdimensionalen Fall ausgenutzt, dass für einen $n$-dimensionalen Vektorraum $V$ und einen Untervektorraum $U\subseteq V$ aus $\dim(U)=n$ schon $V=U$ folgt. Oben haben wir $U=f(V)$ verwendet. In unendlich-dimensionalen Vektorräume gilt das jedoch nicht. Wir können uns das so vorstellen: In einem unendlich-dimensionalen Vektorraum hat ein gleich großer Untervektorraum Platz ohne alles auszufüllen.

Also gilt für Endomorphismen $f\colon V\to V$ eines unendlichdimensionalen Vektorraums $V$ nicht, dass $f$ genau dann surjektiv ist, wenn $f$ injektiv ist. Um das besser zu verstehen, untersuchen wir nun konkrete Gegenbeispiele.

Beispiel (Ein injektiver Endomorphismus, der nicht surjektiv ist)

Sei $V=\{(x_{i})_{i}\mid x_{i}\in \mathbb {R} {\text{ für alle }}i\in \mathbb {N} \}$ der Folgenraum über $\mathbb {R}$. Wir definieren den Endomorphismus

$f\colon V\to V,\quad (x_{1},x_{2},x_{3},\ldots )\mapsto (0,x_{1},x_{2},x_{3},\ldots ).$

Man kann leicht nachprüfen, dass $f$ linear ist. Warum ist $f$ injektiv? Für $x=(x_{1},x_{2},x_{3},\ldots )\in V$ mit $f(x)=0$ gilt $0=x_{1}=x_{2}=x_{3}=\ldots$, also ist $x=0$. Somit folgt $\ker(f)=\{0\}$ und $f$ ist injektiv.

Warum ist $f$ nicht surjektiv? Um das zu sehen, müssen wir einen Vektor in $V$ finden, den $f$ nicht trifft. Sei dafür $(1,0,0,\ldots )\in V$. Egal welches $x\in V$ wir wählen, es gilt für $f(x)$, dass das erste Folgenglied gleich $0$ ist. Also wird $(1,0,0,\ldots )$ nie von $f$ getroffen. Deshalb ist $f$ nicht surjektiv.

Hinweis

Das Vorgehen in diesem Beispiel erinnert an Hilberts Hotel. Dort verschiebt man durch eine Abbildung alle Elemente der Menge $\mathbb {N}$ um $1$. Die Abbildung ist dabei

${\begin{aligned}g\colon \mathbb {N} &\to \mathbb {N} \\n&\mapsto n+1.\end{aligned}}$

Diese Abbildung ist auch injektiv, aber genau wie $f$ nicht surjektiv. Der Unterschied ist, dass $f$ eine lineare Abbildung zwischen Vektorräumen ist und $g$ nur eine Abbildung zwischen Mengen. Wir sehen also hier, dass unendlich-dimensionale Vektorräume ähnlich komische Eigenschaften erfüllen wie unendliche Mengen.

Beispiel (Ein surjektiver Endomorphismus, der nicht injektiv ist)

Wir wählen wieder $V=\{(x_{i})_{i}\mid x_{i}\in \mathbb {R} {\text{ für alle }}i\in \mathbb {N} \}$ den Folgenraum über $\mathbb {R}$. Wir definieren den Endomorphismus

$f\colon V\to V,\quad (x_{1},x_{2},x_{3},\ldots )\mapsto (x_{2},x_{3},x_{4},\ldots ).$

Also ist $f(x)_{i}=x_{i+1}$ für $x=(x_{i})_{i}\in V$. Wieder kann man leicht nachprüfen, dass $f$ linear ist.

Zuerst überprüfen wir, dass $f$ surjektiv ist. Sei dafür $y=(y_{1},y_{2},y_{3}\ldots )\in V$ ein beliebiger Vektor. Wir wollen einen Vektor $x\in V$ finden, für den $f(x)=y$ gilt. Dies gilt für $x=(0,y_{1},y_{2},y_{3},\ldots )\in V$ und damit ist $f$ surjektiv.

Warum ist $f$ nicht injektiv? Um das zu sehen, suchen wir ein $x\in V$ mit $f(x)=0$ und $x\neq 0$. Wir wählen dafür $x=(1,0,0,\ldots )\in V$. Dann ist $x\neq (0,0,0,\ldots )=0$, aber $f(x)=(0,0,0,\ldots )=0$. Somit ist $f$ nicht injektiv.

Die Automorphismengruppe

Wir wissen, dass die Endomorphismen einen Ring mit Eins bilden. Die Automorphismen sind genau alle invertierbaren Endomorphismen. Deshalb sind die Automorphismen eines Vektorraums genau die Einheiten, d. h. die multiplikativ invertierbaren Elemente, des Endomorphismenrings. Die Multiplikation im Endomorphismenring ist die Komposition $\circ$ von Abbildungen. Im folgenden Satz zeigen wir, dass $\operatorname {Aut} _{K}(V)$ eine Gruppe bzgl. dieser Multiplikation ist.

Satz (Automorphismengruppe)

Sei $K$ ein Körper und $V$ ein $K$-Vektorraum. Die Menge $\operatorname {Aut} _{K}(V):=\{\,f\colon V\to V\,|\,f{\text{ Automorphismus}}\,\}$ bildet eine Gruppe bezüglich der Komposition $\circ$.

Es gilt zudem $\operatorname {Aut} _{K}(V)=\operatorname {End} _{K}(V)^{\times }$.

Beweis (Automorphismengruppe)

Wir müssen folgendes zeigen

1. $\operatorname {Aut} _{K}(V)$ ist abgeschlossen bezüglich $\circ$
2. $\circ$ ist assoziativ
3. Es gibt ein neutrales Element bezüglich $\circ$ in $\operatorname {Aut} _{K}(V)$
4. Jedes Element $f$ in $\operatorname {Aut} _{K}(V)$ hat ein multiplikatives Inverses.

Beweisschritt: Abgeschlossenheit bzgl. $\circ$

Wir beweisen, dass für alle Automorphismen $f$ und $g\in \operatorname {Aut} _{K}(V)$ auch $f\circ g\in \operatorname {Aut} _{K}(V)$ gilt.

Seien dafür $f$ und $g\in \operatorname {Aut} _{K}(V)$. Also sind $f$ und $g$ auch Endomorphismen. Weil $\operatorname {End} _{K}(V)$ ein Ring mit Multiplikation $\circ$ bildet, ist $\operatorname {End} _{K}(V)$ abgeschlossen bezüglich $\circ$. Also gilt $f\circ g\in \operatorname {End} _{K}(V)$. Wir müssen also nur noch begründen, dass $f\circ g$ bijektiv ist. Weil $f$ und $g$ bijektiv sind, gibt es jeweils Inverse $f^{-1}\colon V\to V$ und $g^{-1}\colon V\to V$. Wir zeigen nun, dass $g^{-1}\circ f^{-1}\colon V\to V$ die Inverse von $f\circ g$ ist. Es gilt

$(f\circ g)\circ (g^{-1}\circ f^{-1})=f\circ (g\circ g^{-1})\circ f^{-1}=f\circ \operatorname {id} _{V}\circ f^{-1}=f\circ f^{-1}=\operatorname {id} _{V}$

und

$(g^{-1}\circ f^{-1})\circ (f\circ g)=g^{-1}\circ (f^{-1}\circ f)\circ g=g^{-1}\circ \operatorname {id} _{V}\circ g=g^{-1}\circ g=\operatorname {id} _{V}.$

Also hat $f\circ g$ ein Inverses und ist damit bijektiv. Deshalb ist $f\circ g$ ein Automorphismus.

Beweisschritt: Assoziativität von $\circ$

Wir müssen zeigen, dass für alle Automorphismen $f,g$ und $h\in \operatorname {Aut} _{K}(V)$ folgendes gilt

$f\circ (g\circ h)=(f\circ g)\circ h.$

Die Komposition ist sogar für beliebige Abbildungen assoziativ. Trotzdem begründen wir diese Aussage nochmal. Seien dafür $f,g$ und $h\in \operatorname {Aut} _{K}(V)$ und $v\in V$ ein beliebiger Vektor. Dann gilt

${\begin{aligned}&(f\circ (g\circ h))(v)\\=&f((g\circ h)(v))\\=&f(g(h(v)))\\=&(f\circ g)(h(v))\\=&((f\circ g)\circ h)(v).\end{aligned}}$

Da die Abbildungen $f\circ (g\circ h)$ und $(f\circ g)\circ h$ auf allen Vektoren $v\in V$ übereinstimmen, sind sie gleich, d.h. $f\circ (g\circ h)=(f\circ g)\circ h$.

Beweisschritt: Existenz eines Neutralen Elements

Wir müssen ein Element $e\in \operatorname {Aut} _{K}(V)$ finden, so dass für alle $f\in \operatorname {Aut} _{K}(V)$ gilt $f\circ e=f=e\circ f$.

Wir wählen $e:=\operatorname {id} _{V}$. Dann gilt $e\colon V\to V$ und $e$ ist linear. Also ist $e\in \operatorname {End} _{K}(V)$. Außerdem ist $e=\operatorname {id} _{V}$ bijektiv und deshalb gilt $e\in \operatorname {Aut} _{K}(V)$.

Sei $f\in \operatorname {Aut} _{K}(V)$. Es gilt

$f\circ e=f\circ \operatorname {id} _{V}=f=\operatorname {id} _{V}\circ f=e\circ f.$

Also ist $e$ das neutrale Element in $\operatorname {Aut} _{K}(V)$.

Beweisschritt: Existenz Multiplikativer Inverser

Wir beweisen, dass für jedes $f\in \operatorname {Aut} _{K}(V)$ ein Automorphismus $g\in \operatorname {Aut} _{K}(V)$ existiert, so dass $f\circ g=\operatorname {id} _{V}=g\circ f$.

Sei $f\in \operatorname {Aut} _{K}(V)$ ein Automorphismus. Dann ist $f$ bijektiv und somit existiert ein inverse Abbildung $f^{-1}\colon V\to V$, für die gilt $f\circ f^{-1}=\operatorname {id} _{V}=f^{-1}\circ f$. Wir müssen nur noch zeigen, dass $f^{-1}\in \operatorname {Aut} _{K}(V)$. Wir wissen, dass Umkehrabbildungen von linearen Abbildungen linear sind. Folglich ist $f^{-1}$ als Umkehrabbildung der linearen Abbildung $f$ auch linear. Außerdem ist $f^{-1}$ auch bijektiv, weil $f^{-1}$ Umkehrabbildung $f$ hat. Also gilt $f^{-1}\in \operatorname {Aut} _{K}(V)$ und damit ist $f^{-1}$ ein Inverses von $f$ in $\operatorname {Aut} _{K}(V)$.

Die Automorphismen bilden zwar eine Gruppe, sind aber kein Ring mehr. Das liegt daran, dass $\operatorname {Aut} _{K}(V)$ keine additive Struktur mehr hat: Wenn wir zwei Automorphismen $f$ und $g$ von einem Vektorraum $V$ haben, muss $f+g$ nicht unbedingt wieder ein Automorphismus sein. Um das konkret zu machen, betrachten wir ein Beispiel:

Beispiel (Summe von Automorphismen, die kein Automorphismus ist)

Wir betrachten den Vektorraum $V=\mathbb {R} ^{2}$ und definieren die Automorphismen

${\begin{aligned}&f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},\quad &g\colon \mathbb {R} ^{2}&\to \mathbb {R} ^{2}\\[0.3em]&{\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}x\\y\end{pmatrix}},&{\begin{pmatrix}x\\y\end{pmatrix}}&\mapsto {\begin{pmatrix}x\\-y\end{pmatrix}}.\end{aligned}}$

Es ist leicht, zu zeigen, dass $f$ und $g$ linear und bijektiv sind. Also gilt $f,g\in \operatorname {Aut} _{\mathbb {R} }(\mathbb {R} ^{2})$. Es ist

${\begin{aligned}f+g\colon \mathbb {R} ^{2}&\to \mathbb {R} ^{2}\\[0.3em]{\begin{pmatrix}x\\y\end{pmatrix}}&\mapsto {\begin{pmatrix}2x\\0\end{pmatrix}}.\end{aligned}}$

Da diese Abbildung den Vektor $(0,1)^{T}$ nicht trifft, ist sie nicht surjektiv. Also ist $f+g$ nicht bijektiv und somit kein Automorphismus.

Hinweis

Für keinen Vektorraum $V\neq \{0\}$ gilt, dass $\operatorname {Aut} _{K}(V)$ abgeschlossen unter Addition ist.

Für Vektorräume $V$ mit $\dim V\geq 2$ ist die Automorphismengruppe nicht kommutativ. Wie beim Endomorphismenring ist das Verknüpfen der Abbildungen nicht kommutativ. Das untersuchen wir unten in einer Aufgabe.

Aufgaben

Aufgabe (Automorphismus)

Zeige, dass die Abbildung $f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{n},\,(x_{1},x_{2},\ldots ,x_{n})^{T}\mapsto (-2x_{1},-2x_{2},\ldots ,-2x_{n})^{T}$ ein Automorphismus ist.

Lösung (Automorphismus)

Linearität lässt sich leicht nachrechnen. Da Definitions- und Zielbereich gleich sind, ist $f$ also ein Endomorphismus.

Wir wollen nun zeigen, dass $f$ bijektiv ist. Dazu müssen wir zeigen, dass $f$ injektiv und surjektiv ist.

Wir beginnen mit der Injektivität. Seien $x=(x_{1},\ldots ,x_{n})^{T}$ und $y=(y_{1},\ldots ,y_{n})^{T}\in \mathbb {R} ^{n}$ mit $f(x)=f(y)$. Dann gilt für $i=1,\ldots ,n$, dass $-2x_{i}=-2y_{i}$, also $x_{i}=y_{i}$ und somit $x=y$. Dies zeigt die Injektivität.

Nun zeigen wir die Surjektivität. Sei dazu $x=(x_{1},\ldots ,x_{n})^{T}\in \mathbb {R} ^{n}$. Definiere $y:=(-x_{1}/2,\ldots ,-x_{n}/2)^{T}\in \mathbb {R} ^{n}$. Dann gilt $f(y)=x$. Also ist $f$ surjektiv.

Wir haben also gezeigt, dass $f$ ein Automorphismus ist.

Aufgabe (Transformation im Raum der Fibonacci-Folgen)

Sei $K$ ein Körper und $V$ der Vektorraum der Fibonacci-Folgen

$V=\{(x_{i})_{i\in \mathbb {N} }\in \omega \mid x_{n}+x_{n+1}=x_{n+2}{\text{ für alle }}n\in \mathbb {N} \},$

wobei $\omega$ der Raum aller Folgen in $K$ ist. Zeige:

1. $V$ ist isomorph zu $K^{2}$.
2. Es gibt einen Endomorphismus $f\colon V\to V$, der die ersten beiden Einträge jeder Folge vertauscht, das heißt, es gilt $f((x_{i})_{i\in \mathbb {N} })_{1}=x_{2}$ und $f((x_{i})_{i\in \mathbb {N} })_{2}=x_{1}$ für alle $(x_{i})_{i\in \mathbb {N} }\in V$.
3. $f$ ist ein Automorphismus.

Lösung (Transformation im Raum der Fibonacci-Folgen)

Beweisschritt: $V\cong K^{2}$

Wir zeigen, dass

$\Phi \colon V\to K^{2},\quad (x_{i})_{i\in \mathbb {N} }\mapsto {\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}$

ein Isomorphismus ist. Die Linearität lässt sich leicht nachrechnen.

Für die Injektivität zeigen wir $\ker \Phi =\{0\}$. Sei also $(x_{i})_{i\in \mathbb {N} }\in V$ mit $\Phi ((x_{i})_{i\in \mathbb {N} })=(0,0)^{T}$, d.h. $x_{1}=x_{2}=0$. Wir zeigen $x_{n}=0$ für alle $n\in \mathbb {N}$ mit vollständiger Induktion. Nach Annahme gilt die Aussage für $n=1,2$. Damit ist der Induktionsanfang gezeigt. Sei nun $n>2$. Für den Beweis des Induktionsschritts müssen wir $x_{n}=0$ zeigen und nehmen dafür als Induktionsvoraussetzung an, dass die Aussage $x_{i}=0$ für alle $i\in \{1,2,\ldots ,n-1\}$ gilt. Per Definition der Folge $(x_{i})_{i\in \mathbb {N} }\in V$ folgt $x_{n}=x_{n-1}+x_{n-2}=0+0=0$.

Für die Surjektivität benutzen wir, dass jede Folge in $V$ durch Angabe der ersten beiden Folgenglieder definiert werden kann: Sei $(a,b)^{T}\in K^{2}$. Wir definieren $(x_{i})_{i\in \mathbb {N} }$ wie im Beweis der Injektivität induktiv durch $x_{1}=a$, $x_{2}=b$ und $x_{i}:=x_{i-1}+x_{i-2}$. Dann gilt $(x_{i})_{i\in \mathbb {N} }\in V$ und $\Phi ((x_{i})_{i\in \mathbb {N} })=(a,b)^{T}$.

Beweisschritt: Es gibt einen Endomorphismus $f\colon V\to V$, der die ersten beiden Einträge jeder Folge vertauscht.

Wir benutzen den Isomorphismus $\Phi$ aus dem ersten Teil der Aufgabe. Offenbar ist

$g\colon K^{2}\to K^{2},\quad {\begin{pmatrix}a\\b\end{pmatrix}}\mapsto {\begin{pmatrix}b\\a\end{pmatrix}}$

linear und bildet von $K^{2}$ nach $K^{2}$ ab, ist also ein Endomorphismus. Damit ist auch $f:=\Phi ^{-1}\circ g\circ \Phi$ als Verkettung linearer Abbildungen linear. Da $f$ von $V$ nach $V$ abbildet, ist $f$ ein Endomorphismus, und per Konstruktion gilt

$\Phi (f((x_{i})_{i\in \mathbb {N} }))=g(\Phi ((x_{i})_{i\in \mathbb {N} }))=g{\Bigl (}{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}{\Bigr )}={\begin{pmatrix}x_{2}\\x_{1}\end{pmatrix}}$

für alle $(x_{i})_{i\in \mathbb {N} }\in V$. Also vertauscht $f$ die ersten beiden Einträge jeder Folge.

Beweisschritt: $f$ ist ein Automorphismus.

Wir müssen zeigen, dass $f$ ein Isomorphismus ist. Da $\Phi$ ein Isomorphismus ist, ist $f=\Phi ^{-1}\circ g\circ \Phi$ ein Isomorphismus genau dann wenn $g$ ein Isomorphismus ist. Der Endomorphismus $g$ vertauscht einfach nur die beiden Komponenten eines Vektors in $K^{2}$, bildet also die (geordnete) Basis $(e_{1},e_{2})$ von $K^{2}$ auf die Basis $(e_{2},e_{1})$ ab. Da eine lineare Abbildung genau dann bijektiv ist, wenn sie Basen auf Basen abbildet, ist $g$ ein Isomorphismus.

Aufgabe (Scherungen sind Automorphismen)

Sei $\lambda \in \mathbb {R}$ ein Skalar. Wir betrachten die Abbildung $f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},\ (x,y)^{T}\mapsto (x+\lambda y,y)^{T}$. Zeige, dass $f$ ein Automorphismus ist.

Lösung (Scherungen sind Automorphismen)

Die Linearität von $f$ lässt sich leicht nachprüfen. Da $f$ den $\mathbb {R} ^{2}$ auf sich selbst abbildet, ist $f$ ein Endomorphismus und es bleibt lediglich die Bijektivität zu zeigen.

Wir beweisen die Injektivität, indem wir $\ker(f)=\{(0,0)^{T}\}$ zeigen. Sei $u=(u_{1},u_{2})^{T}\in \ker(f)$, das heißt, es gilt $f(u)=(0,0)^{T}$. Wir wollen $u=(0,0)^{T}$ zeigen. Da $f(u)=(u_{1}+\lambda u_{2},u_{2})^{T}=(0,0)^{T}$ gilt, erhalten wir $u_{2}=0$ aus der zweiten Vektorkomponente. Daraus folgt nun $0=u_{1}+\lambda \cdot 0=u_{1}$ und es gilt $u=(0,0)$. Damit ist $f$ injektiv.

Als zweites müssen wir zeigen, dass $f$ surjektiv ist. Sei dafür $v=(v_{1},v_{2})^{T}\in \mathbb {R} ^{2}$; wir müssen zeigen, dass es ein $u=(u_{1},u_{2})^{T}\in \mathbb {R} ^{2}$ mit $f(u)=v$ gibt. Wenn wir die Definition von $f$ einsetzen, muss der gesuchte Vektor $u$ damit $(u_{1}+\lambda u_{2},u_{2})^{T}=(v_{1},v_{2})^{T}$ erfüllen. Das heißt, es muss $u_{2}=v_{2}$ gelten. Hieraus erhalten wir $u_{1}+\lambda v_{2}=v_{1}$, also $u_{1}=v_{1}-\lambda v_{2}$. Setzen wir $u:=(v_{1}-\lambda v_{2},v_{2})^{T}\in \mathbb {R} ^{2}$, so gilt

$f(u)=f{\begin{pmatrix}v_{1}-\lambda v_{2}\\v_{2}\end{pmatrix}}={\begin{pmatrix}(v_{1}-\lambda v_{2})+\lambda v_{2}\\v_{2}\end{pmatrix}}={\begin{pmatrix}v_{1}\\v_{2}\end{pmatrix}}=v.$

Also ist $f$ surjektiv.

Da $f$ bijektiv und ein Endomorphismus ist, ist $f$ ein Automorphismus.

Aufgabe (Nicht-Kommutativität im Endomorphismenring)

Sei $V$ ein $n$-dimensionaler $K$-Vektorraum mit $n\geq 2$. Zeige: Der Endomorphismenring $\operatorname {End} _{K}(V)$ ist nicht kommutativ.

Lösung (Nicht-Kommutativität im Endomorphismenring)

Sei $B=\{v_{1},\ldots ,v_{n}\}$ eine Basis von $V$, wobei nach Annahme $n\geq 2$ gilt. Wir definieren zwei nichtkommutierende Endomorphismen $f,g\in \operatorname {Hom} _{K}(V)$ nach dem Prinzip der linearen Fortsetzung, indem wir die Bilder der Basisvektoren vorgeben: Für $k\in \{1,\ldots ,n\}$ setze

$f:V\to V,\quad f(v_{k})={\begin{cases}v_{2}{\text{ falls }}k=1,\\v_{1}{\text{ falls }}k=2,\\v_{k}{\text{ sonst,}}\end{cases}}$

und

$g:V\to V,\quad g(v_{k})={\begin{cases}0{\text{ falls }}k=1,\\v_{k}{\text{ sonst.}}\end{cases}}$

Die Abbildung $f$ vertauscht also die ersten beiden Basisvektoren, während $g$ den ersten Basisvektor auf den Nullvektor abbildet. Bei der Definition von $f$ und $g$ haben wir gebraucht, dass es $n\geq 2$ Basisvektoren gibt. Es gilt für $k\in \{1,\ldots ,n\}$

$(f\circ g)(v_{k})=f(g(v_{k}))={\begin{cases}0{\text{ falls }}k=1,\\v_{1}{\text{ falls }}k=2,\\v_{k}{\text{ sonst,}}\end{cases}}$

aber

$(g\circ f)(v_{k})=g(f(v_{k}))={\begin{cases}v_{2}{\text{ falls }}k=1,\\0{\text{ falls }}k=2,\\v_{k}{\text{ sonst.}}\end{cases}}$

Da der Basisvektor $v_{2}$ als Element der Basis $B$ von $V$ nicht der Nullvektor sein kann, folgt insbesondere

$(g\circ f)(v_{1})=v_{2}\neq 0=(f\circ g)(v_{1}).$

Also gilt $g\circ f\neq f\circ g$. Damit ist der Endomorphismenring $\operatorname {End} _{K}(V)$ nicht kommutativ, falls $\dim(V)\geq 2$.

Aufgabe (Kommutativität im Endomorphismenring)

Sei $V$ ein eindimensionaler $K$-Vektorraum, d.h. $\dim(V)=1$. Zeige: Der Endomorphismenring $\operatorname {End} _{K}(V)$ ist kommutativ.

Lösung (Kommutativität im Endomorphismenring)

Sei $B=\{b\}$ eine Basis von $V$ und seien $f,g\in \operatorname {End} _{K}(V)$ beliebig. Endomorphismen sind durch die Bilder der Basisvektoren schon eindeutig bestimmt. Da es wegen $\dim(V)=1$ nur einen Basisvektor gibt, gilt $f(b),g(b)\in \operatorname {span} (V)$ und damit

$f(b)=\lambda _{1}\cdot b\quad {\text{und}}\quad g(b)=\lambda _{2}\cdot b$

für gewisse $\lambda _{1},\lambda _{2}\in K$. Wegen $V=\operatorname {span} \{b\}$ ist jedes $v\in V$ von der Form $v=\mu b$ für ein $\mu \in K$. Mit der Linearität von $f$ und der Kommutativität der Multiplikation in $K$ folgt

$f(v)=f(\mu b)=\mu f(b)=\mu (\lambda _{1}b)=(\mu \lambda _{1})b=(\lambda _{1}\mu )b=\lambda _{1}(\mu b)=\lambda _{1}v.$

Analog kann man $g(v)=\lambda _{2}v$ für beliebiges $v\in V$ zeigen und es folgt

$f\colon V\to V,\;v\mapsto \lambda _{1}\cdot v\quad {\text{und}}\quad g\colon V\to V,\;v\mapsto \lambda _{2}\cdot v.$

Somit gilt für alle $v\in V$

$(f\circ g)(v)=f(g(v))=f(\lambda _{2}v)=\lambda _{1}(\lambda _{2}v)=(\lambda _{1}\lambda _{2})v{\overset {(*)}{=}}(\lambda _{2}\lambda _{1})v=\lambda _{2}(\lambda _{1}v)=g(\lambda _{1}v)=g(f(v))=(g\circ f)(v),$

wobei wir in $(*)$ die Kommutativität der Multiplikation in $K$ ausgenutzt haben.

Hinweis

In den obigen beiden Aufgaben haben wir gesehen, dass $\operatorname {End} _{K}(V)$ kommutativ ist, wenn $\dim(V)=1$ und nicht kommutativ, wenn $\dim(V)\geq 2$. Was gilt für $\dim(V)=0$? Wenn $\dim(V)=0$ gilt, ist $V$ der Nullvektorraum. Es gibt nur einen Endomorphismus über dem Nullraum $V=\{0\}$. Dieser Endomorphismus ist die Nullabbildung $e\colon \{0\}\to \{0\},\ 0\mapsto 0$. Also gilt $\operatorname {End} _{K}(V)=\{e\}$. Da der Ring nur aus einem Element besteht, ist $\operatorname {End} _{K}(V)$ kommutativ.

Somit gilt: $\operatorname {End} _{K}(V)$ ist genau dann kommutativ, wenn $\dim(V)\leq 1$.