Größe
Formelzeichen
Name der Einheit
Einheitenzeichen
Beziehung zwischen den Einheiten
Arbeit, Energie
W
,
E
{\displaystyle W,E}
Joule
J
{\displaystyle \mathrm {J} }
1
J
=
1
N
⋅
m
=
1
k
g
⋅
m
2
s
2
{\displaystyle 1\,\mathrm {J} =1\,\mathrm {N} \cdot \mathrm {m} =1{\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{2}}}}
Beschleunigung
a
{\displaystyle a}
Meter durch Quadratsekunde
m
s
2
{\displaystyle {\frac {\mathrm {m} }{\mathrm {s} ^{2}}}}
Dichte
ρ
{\displaystyle \rho }
Masse (Kilogramm) geteilt durch Volumen (Kubikmeter)
k
g
m
3
{\displaystyle {\frac {\mathrm {kg} }{\mathrm {m} ^{3}}}}
1
k
g
m
3
=
0,001
g
c
m
3
{\displaystyle 1{\frac {\mathrm {kg} }{\mathrm {m} ^{3}}}=0{,}001{\frac {\mathrm {g} }{\mathrm {cm} ^{3}}}}
Drehimpuls
L
{\displaystyle L}
Newtonmetersekunde
N
⋅
m
⋅
s
{\displaystyle \mathrm {N} \cdot \mathrm {m} \cdot \mathrm {s} }
1
N
⋅
m
⋅
s
=
1
k
g
⋅
m
2
s
{\displaystyle \mathrm {1} \!\,\mathrm {N} \cdot \mathrm {m} \cdot \mathrm {s} =\mathrm {1} \mathrm {kg} \cdot {\frac {\mathrm {m^{2}} }{\mathrm {s} }}}
Drehmoment
M
{\displaystyle M}
Newtonmeter
N
⋅
m
{\displaystyle \mathrm {N} \cdot \mathrm {m} }
1
N
⋅
m
=
1
k
g
⋅
m
2
s
2
{\displaystyle \mathrm {1} \,\mathrm {N} \cdot \mathrm {m} =1\,{\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{2}}}}
Druck
p
{\displaystyle p}
Pascal
P
a
{\displaystyle \mathrm {Pa} }
1
P
a
=
1
N
m
2
=
1
k
g
m
⋅
s
2
{\displaystyle \mathrm {1} \,\mathrm {Pa} =\mathrm {1} {\frac {\mathrm {N} }{\mathrm {m} ^{2}}}=1{\frac {\mathrm {kg} }{\mathrm {m} \cdot \mathrm {s} ^{2}}}}
Drehzahl
n
{\displaystyle n}
durch Sekunde
1
s
{\displaystyle {\frac {1}{\mathrm {s} }}}
1
s
=
60
1
m
i
n
{\displaystyle {\frac {1}{\mathrm {s} }}=60{\frac {1}{\mathrm {min} }}}
Federkonstante
D
{\displaystyle D}
k
{\displaystyle k}
Newton durch Meter
N
m
{\displaystyle {\frac {\mathrm {N} }{\mathrm {m} }}}
1
N
m
=
1
k
g
s
2
{\displaystyle 1\,{\frac {\mathrm {N} }{\mathrm {m} }}=1\,{\frac {\mathrm {kg} }{\mathrm {s} ^{2}}}}
Fläche, Flächeninhalt
A
{\displaystyle A}
Quadratmeter
m
2
{\displaystyle \mathrm {m} ^{2}}
1
m
2
=
1
m
⋅
1
m
{\displaystyle 1\,\mathrm {m} ^{2}=1\mathrm {m} \cdot 1\mathrm {m} }
Frequenz
f
{\displaystyle f}
ν
{\displaystyle \nu }
Hertz
H
z
{\displaystyle \mathrm {Hz} }
1
H
z
=
1
s
{\displaystyle 1\,\mathrm {Hz} ={\frac {1}{\mathrm {s} }}}
Geschwindigkeit
v
{\displaystyle v}
Meter durch Sekunde
m
s
{\displaystyle {\frac {\mathrm {m} }{\mathrm {s} }}}
1
m
s
=
3
,
6
k
m
h
{\displaystyle 1\,{\frac {\mathrm {m} }{\mathrm {s} }}=3,6{\frac {\mathrm {km} }{\mathrm {h} }}}
Impuls
p
{\displaystyle p}
Kilogrammmeter durch Sekunde
k
g
⋅
m
s
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} }}}
1
k
g
⋅
m
s
=
1
N
⋅
s
{\displaystyle 1\,{\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} }}=1\mathrm {N} \cdot \mathrm {s} }
Kraft
F
{\displaystyle F}
Newton
N
{\displaystyle \mathrm {N} }
1
N
=
1
k
g
⋅
m
s
2
{\displaystyle 1\,\mathrm {N} =1{\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} ^{2}}}}
Weg
s
{\displaystyle s}
Meter
m
{\displaystyle \mathrm {m} }
Basiseinheit
Leistung, Energiestrom
P
{\displaystyle P}
Watt
W
{\displaystyle \mathrm {W} }
1
W
=
1
J
s
=
1
N
⋅
m
s
=
1
k
g
⋅
m
2
s
3
{\displaystyle 1\mathrm {W} =1\,{\frac {\mathrm {J} }{\mathrm {s} }}=1\,{\frac {\mathrm {N} \cdot \mathrm {m} }{\mathrm {s} }}=1\,{\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{3}}}}
Masse
m
{\displaystyle m}
Kilogramm
k
g
{\displaystyle \mathrm {kg} }
Basiseinheit
Schwingungsdauer, Periodendauer
T
{\displaystyle T}
Sekunde
s
{\displaystyle \mathrm {s} }
Trägheitsmoment
J
{\displaystyle J}
Kilogramm mal Quadratmeter
k
g
⋅
m
2
{\displaystyle \mathrm {kg} \cdot \mathrm {m} ^{2}}
Volumen
V
{\displaystyle V}
Kubikmeter
m
3
{\displaystyle \mathrm {m} ^{3}}
1
m
3
=
1
m
⋅
1
m
⋅
1
m
{\displaystyle 1\,\mathrm {m} ^{3}=1\mathrm {m} \cdot 1\mathrm {m} \cdot 1\mathrm {m} }
Wellenlänge
λ
{\displaystyle \lambda }
Meter
m
{\displaystyle \mathrm {m} }
Winkelbeschleunigung
α
{\displaystyle \alpha }
Radiant durch Quadratsekunde
r
a
d
s
2
{\displaystyle {\frac {\mathrm {rad} }{\mathrm {s} ^{2}}}}
1
r
a
d
s
2
=
1
s
2
{\displaystyle 1\,{\frac {\mathrm {rad} }{\mathrm {s} ^{2}}}={\frac {1}{\mathrm {s} ^{2}}}}
Winkelgeschwindigkeit
ω
{\displaystyle \omega }
Radiant durch Sekunde
r
a
d
s
{\displaystyle {\frac {\mathrm {rad} }{\mathrm {s} }}}
1
r
a
d
s
=
1
s
{\displaystyle 1\,{\frac {\mathrm {rad} }{\mathrm {s} }}={\frac {1}{\mathrm {s} }}}
Zeit
t
{\displaystyle t}
Sekunde
s
{\displaystyle \mathrm {s} }
Basiseinheit
Definition. Geschwindigkeit.
Für eine Punktmasse, die zum Zeitpunkt t die Strecke s (t ) zurückgelegt hat, ist
v
(
t
)
=
d
s
d
t
≈
s
(
t
)
−
s
(
t
0
)
t
−
t
0
{\displaystyle v(t)={\frac {\mathrm {d} s}{\mathrm {d} t}}\approx {\frac {s(t)-s(t_{0})}{t-t_{0}}}}
t
≈
t
0
{\displaystyle t\approx t_{0}}
die momentane Geschwindigkeit zum Zeitpunkt t .
Einheiten
m/s = 3,6 km/h = (3600/1852) kn = (3600/1609,344) mph
m: Meter, s: Sekunde, km: Kilometer, h: Stunde,
Definition. Durchschnittsgeschwindigkeit.
v
¯
:=
Δ
s
Δ
t
=
s
(
t
)
−
s
(
t
0
)
t
−
t
0
.
{\displaystyle {\bar {v}}:={\frac {\Delta s}{\Delta t}}={\frac {s(t)-s(t_{0})}{t-t_{0}}}.}
Bei einer gleichförmigen Bewegung stimmt die Durchschnittsgeschwindigkeit mit der momentanen Geschwindigkeit überein.
Definition. Geschwindigkeitsvektor.
Für eine Parameterkurve, die einer Punktmasse zu jedem Zeitpunkt t einen Ort
r
→
(
t
)
{\displaystyle {\vec {r}}(t)}
v
→
(
t
)
:=
d
r
→
d
t
{\displaystyle {\vec {v}}(t):={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}}
der momentane Geschwindigkeitsvektor zum Zeitpunkt t .
Der Betrag
v
=
|
v
→
|
{\displaystyle v=|{\vec {v}}|}
Die Größe
s
(
t
)
:=
s
(
t
0
)
+
∫
t
0
t
|
v
→
(
t
)
|
d
t
{\displaystyle s(t):=s(t_{0})+\int _{t_{0}}^{t}|{\vec {v}}(t)|\,\mathrm {d} t}
ist die zurückgelegte Strecke. Es gilt
v
(
t
)
=
|
d
r
→
d
t
|
=
d
s
d
t
.
{\displaystyle v(t)={\bigg |}{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}{\bigg |}={\frac {\mathrm {d} s}{\mathrm {d} t}}.}
Definition. Beschleunigung in eine Richtung.
Wird durch x (t ) eine Bewegung in eine Richtung beschrieben, dann versteht man unter
a
x
(
t
)
:=
v
x
′
(
t
)
≈
v
x
(
t
)
−
v
x
(
t
0
)
t
−
t
0
{\displaystyle a_{x}(t):=v_{x}'(t)\approx {\frac {v_{x}(t)-v_{x}(t_{0})}{t-t_{0}}}}
t
≈
t
0
{\displaystyle t\approx t_{0}}
die momentane Beschleunigung zum Zeitpunkt t , wobei
v
x
(
t
)
=
x
′
(
t
)
{\displaystyle v_{x}(t)=x'(t)}
die Geschwindigkeit ist.
Die Beschleunigung ist die zweite Ableitung des Ortes nach der Zeit:
a
x
(
t
)
=
x
″
(
t
)
.
{\displaystyle a_{x}(t)=x''(t).}
Definition. Beschleunigungsvektor.
Der momentane Beschleunigungsvektor zum Zeitpunkt t ist
a
→
(
t
)
:=
v
→
′
(
t
)
=
a
x
e
→
x
+
a
y
e
→
y
+
a
z
e
→
z
.
{\displaystyle {\vec {a}}(t):={\vec {v}}'(t)=a_{x}{\vec {e}}_{x}+a_{y}{\vec {e}}_{y}+a_{z}{\vec {e}}_{z}.}
Für die Komponenten gilt dabei
a
x
=
v
x
′
(
t
)
≈
v
x
(
t
)
−
v
x
(
t
0
)
t
−
t
0
,
{\displaystyle a_{x}=v_{x}'(t)\approx {\frac {v_{x}(t)-v_{x}(t_{0})}{t-t_{0}}},}
a
y
=
v
y
′
(
t
)
≈
v
y
(
t
)
−
v
y
(
t
0
)
t
−
t
0
,
{\displaystyle a_{y}=v_{y}'(t)\approx {\frac {v_{y}(t)-v_{y}(t_{0})}{t-t_{0}}},}
a
z
=
v
z
′
(
t
)
≈
v
z
(
t
)
−
v
z
(
t
0
)
t
−
t
0
{\displaystyle a_{z}=v_{z}'(t)\approx {\frac {v_{z}(t)-v_{z}(t_{0})}{t-t_{0}}}}
für
t
≈
t
0
{\displaystyle t\approx t_{0}}
a
=
|
a
→
|
=
a
x
2
+
a
y
2
+
a
z
2
{\displaystyle a=|{\vec {a}}|={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}}
wird Beschleunigung genannt.
Bei einer geradlinigen Bewegung gilt
a
(
t
)
=
v
′
(
t
)
.
{\displaystyle a(t)=v'(t).}
Bei einer krummlinigen Bewegung zerfällt die Beschleunigung jedoch in zwei Komponenten:
die Tangentialbeschleunigung
a
tangential
=
v
′
(
t
)
{\displaystyle a_{\text{tangential}}=v'(t)}
und die Normalbeschleunigung
a
normal
=
v
2
R
.
{\displaystyle a_{\text{normal}}={\frac {v^{2}}{R}}.}
Es gilt
a
→
=
a
tangential
t
^
+
a
normal
n
^
{\displaystyle {\vec {a}}=a_{\text{tangential}}{\hat {t}}+a_{\text{normal}}{\hat {n}}}
und
a
=
a
tangential
2
+
a
normal
2
.
{\displaystyle a={\sqrt {a_{\text{tangential}}^{2}+a_{\text{normal}}^{2}}}.}
Hierbei ist
R
{\displaystyle R}
r
→
(
t
)
{\displaystyle {\vec {r}}(t)}
t
^
{\displaystyle {\hat {t}}}
r
→
(
t
)
{\displaystyle {\vec {r}}(t)}
n
^
{\displaystyle {\hat {n}}}
r
→
(
t
)
{\displaystyle {\vec {r}}(t)}
Definition. Impuls in eine Richtung.
Wird durch den zeitlich veränderlichen Ort x (t ) die Bewegung einer Punktmasse in eine Richtung beschrieben, dann ist der Impuls das Produkt aus Masse und Geschwindigkeit zum Zeitpunkt t :
p
x
(
t
)
:=
m
(
t
)
⋅
v
x
(
t
)
.
{\displaystyle p_{x}(t):=m(t)\cdot v_{x}(t).}
Definition. Impulsvektor.
Unter dem Impulsvektor versteht man das Produkt aus Masse und Geschwindigkeitsvektor:
p
→
:=
m
v
→
.
{\displaystyle {\vec {p}}:=m{\vec {v}}.}
Impulsvektor und Geschwindigkeitsvektor zeigen in die gleiche Richtung.
Für die Komponenten gilt:
p x = m v x ,p y = m v y ,p z = m v z .Für die Beträge gilt:
p = m v .
Definition. Kraft in eine Richtung.
Wird durch den zeitlich veränderlichen Ort x (t ) eine Bewegung in eine Richtung beschrieben, dann versteht man unter
F
x
(
t
)
:=
p
x
′
(
t
)
≈
p
x
(
t
)
−
p
x
(
t
0
)
t
−
t
0
{\displaystyle F_{x}(t):=p_{x}'(t)\approx {\frac {p_{x}(t)-p_{x}(t_{0})}{t-t_{0}}}}
t
≈
t
0
{\displaystyle t\approx t_{0}}
die Kraft zum Zeitpunkt t .
Für eine zeitlich konstante Masse m gilt:
F
x
=
m
a
x
.
{\displaystyle F_{x}=ma_{x}.}
Einheit
[
F
]
=
N
:=
k
g
⋅
m
s
2
{\displaystyle [F]=\mathrm {N} :={\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} ^{2}}}}
N: Newton, kg: Kilogramm, m: Meter, s: Sekunde
Definition. Kraftvektor.
Unter dem Kraftvektor zum Zeitpunkt t versteht man die Ableitung des Impulsvektors nach der Zeit:
F
→
(
t
)
:=
p
→
′
(
t
)
=
p
x
′
(
t
)
e
→
x
+
p
y
′
(
t
)
e
→
y
+
p
z
′
(
t
)
e
→
z
.
{\displaystyle {\vec {F}}(t):={\vec {p}}'(t)=p_{x}'(t){\vec {e}}_{x}+p_{y}'(t){\vec {e}}_{y}+p_{z}'(t){\vec {e}}_{z}.}
Für eine zeitlich konstante Masse m gilt:
F
→
=
m
a
→
.
{\displaystyle {\vec {F}}=m{\vec {a}}.}
Für die betragsmäßige Kraft gilt dann
F
=
m
a
{\displaystyle F=ma}
mit
F
:=
|
F
→
|
{\displaystyle F:=|{\vec {F}}|}
a
:=
|
a
→
|
{\displaystyle a:=|{\vec {a}}|}
Für eine zeitlich veränderliche Masse ergibt sich jedoch
F
→
=
d
m
d
t
v
→
+
m
a
→
.
{\displaystyle {\vec {F}}={\frac {\mathrm {d} m}{\mathrm {d} t}}\,{\vec {v}}+m{\vec {a}}.}
Definition. Arbeit bei einer geradlinigen Bewegung.
Muss während einer geradlinigen Bewegung von einem Ort x 1 zu einem Ort x 2 gegen die Kraft F (x ) gearbeitet werden, dann ist
W
:=
∫
x
1
x
2
F
(
x
)
d
x
=
∫
t
1
t
2
F
(
x
(
t
)
)
v
(
t
)
d
t
{\displaystyle W:=\int _{x_{1}}^{x_{2}}F(x)\,\mathrm {d} x=\int _{t_{1}}^{t_{2}}F(x(t))\,v(t)\,\mathrm {d} t}
die aufgebrachte Arbeit, wobei
x
1
=
x
(
t
1
)
{\displaystyle x_{1}=x(t_{1})}
x
2
=
x
(
t
2
)
{\displaystyle x_{2}=x(t_{2})}
Für eine konstante Kraft F gilt
W
=
F
Δ
x
=
F
⋅
(
x
2
−
x
1
)
.
{\displaystyle W=F\Delta x=F\cdot (x_{2}-x_{1}).}
Einheit
[
W
]
=
J
:=
k
g
⋅
m
2
s
2
=
N
⋅
m
=
W
⋅
s
=
V
⋅
A
⋅
s
=
V
⋅
C
{\displaystyle [W]=\mathrm {J} :={\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{2}}}=\mathrm {N} \cdot \mathrm {m} =\mathrm {W} \cdot \mathrm {s} =\mathrm {V} \cdot \mathrm {A} \cdot s=\mathrm {V} \cdot \mathrm {C} }
J: Joule, kg: Kilogramm, m: Meter, s: Sekunde, N: Newton, W: Watt, V: Volt, A: Ampere, C: Coulomb
Definition. Arbeit.
W
:=
∫
γ
⟨
F
→
(
r
→
)
,
d
r
→
⟩
:=
∫
t
1
t
2
⟨
F
→
(
r
→
(
t
)
)
,
v
→
(
t
)
⟩
d
t
,
{\displaystyle W:=\int _{\gamma }\langle {\vec {F}}({\vec {r}}),\mathrm {d} {\vec {r}}\rangle :=\int _{t_{1}}^{t_{2}}\langle {\vec {F}}({\vec {r}}(t)),{\vec {v}}(t)\rangle \,\mathrm {d} t,}
wobei
γ
(
t
)
=
r
→
(
t
)
{\displaystyle \gamma (t)={\vec {r}}(t)}
r
→
(
t
1
)
{\displaystyle {\vec {r}}(t_{1})}
r
→
(
t
2
)
{\displaystyle {\vec {r}}(t_{2})}
Für das Skalarprodukt gilt
⟨
F
→
,
v
→
⟩
=
F
x
v
x
+
F
y
v
y
+
F
z
v
z
,
{\displaystyle \langle {\vec {F}},{\vec {v}}\rangle =F_{x}v_{x}+F_{y}v_{y}+F_{z}v_{z},}
sofern eine Orthonormalbasis vorliegt.
Für eine konstante Kraft
F
→
{\displaystyle {\vec {F}}}
W
=
⟨
F
→
,
Δ
r
→
⟩
=
⟨
F
→
,
r
→
(
t
2
)
−
r
→
(
t
1
)
⟩
.
{\displaystyle W=\langle {\vec {F}},\Delta {\vec {r}}\rangle =\langle {\vec {F}},{\vec {r}}(t_{2})-{\vec {r}}(t_{1})\rangle .}
Die Anheftung der selben konstanten Kraft an jeden Ort ist ein Potentialfeld, da die Arbeit unabhängig vom gewählten Weg von
r
→
1
=
r
→
(
t
1
)
{\displaystyle {\vec {r}}_{1}={\vec {r}}(t_{1})}
r
→
2
=
r
→
(
t
2
)
{\displaystyle {\vec {r}}_{2}={\vec {r}}(t_{2})}
s
:=
|
r
→
2
−
r
→
1
|
{\displaystyle s:=|{\vec {r}}_{2}-{\vec {r}}_{1}|}
den Abstand, das ist die kürzeste Streckenlänge, dann ergibt sich die Formel
W
=
F
⋅
s
⋅
cos
φ
{\displaystyle W=F\cdot s\cdot \cos \varphi }
mit
F
:=
|
F
→
|
{\displaystyle F:=|{\vec {F}}|}
φ
:=
∠
(
F
→
,
Δ
r
→
)
.
{\displaystyle \varphi :=\angle ({\vec {F}},\Delta {\vec {r}}).}
Beschleunigungsarbeit m von einer Geschwindigkeit v 0 auf eine Geschwindigkeit v beschleunigt, dann muss gegen die Trägheit der Masse gearbeitet werden. Die Beschleunigungsarbeit beträgt
W
B
=
1
2
m
v
2
−
1
2
m
v
0
2
.
{\displaystyle W_{B}={\frac {1}{2}}mv^{2}-{\frac {1}{2}}mv_{0}^{2}.}
Die Beschleunigungsarbeit ist neben der Masse und der Anfangsgeschwindigkeit nur von der erreichten Endgeschwindigkeit abhängig. Ob die Punktmasse gleichförmig beschleunigt wurde oder nicht, ist dabei unwesentlich.
Hubarbeit g als näherungsweise konstant angenommen werden. Demnach ist auch die Kraft
F
g
=
m
g
{\displaystyle F_{g}=mg}
näherungsweise konstant. Um eine Punktmasse m um eine Höhe h zu heben, muss nun die Hubarbeit
W
H
=
F
g
h
=
m
g
h
.
{\displaystyle W_{H}=F_{g}\,h=m\,g\,h.}
aufgebracht werden.
Spannarbeit x die Kraft
F
=
k
x
{\displaystyle F=kx}
entgegen, wobei k die Federkonstante ist.
Bei der Auslenkung der Feder von x 0 bis x muss die Spannarbeit
W
Spann
=
1
2
k
x
2
−
1
2
k
x
0
2
{\displaystyle W_{\text{Spann}}={\frac {1}{2}}kx^{2}-{\frac {1}{2}}kx_{0}^{2}}
aufgebracht werden.
Kinetische Energie
Kinetische Energie einer Masse
m
{\displaystyle m}
v
{\displaystyle v}
E
kin
=
1
2
m
⋅
v
2
bei
v
≪
c
{\displaystyle E_{\text{kin}}={\frac {1}{2}}\,m\cdot v^{2}\quad {\text{bei}}\ v\ll c}
mit c = Lichtgeschwindigkeit .
Einheiten
Energie
Masse
Geschwindigkeit
[E ] = J
[m ] = kg
[v ] = m/s = Ns/kg
J: Joule, kg: Kilogramm, m: Meter, s: Sekunde, N: Newton
Kartesische Koordinaten
E
kin
=
1
2
m
(
x
˙
2
+
y
˙
2
+
z
˙
2
)
{\displaystyle E_{\text{kin}}={\tfrac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})}
Polarkoordinaten
E
kin
=
1
2
m
(
r
˙
2
+
r
2
φ
˙
2
)
{\displaystyle E_{\text{kin}}={\tfrac {1}{2}}m({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2})}
Zylinderkoordinaten
E
kin
=
1
2
m
(
r
˙
2
+
r
2
φ
˙
2
+
z
˙
2
)
{\displaystyle E_{\text{kin}}={\tfrac {1}{2}}m({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2}+{\dot {z}}^{2})}
Kugelkoordinaten
E
kin
=
1
2
m
(
r
˙
2
+
r
2
θ
˙
2
+
r
2
φ
˙
2
sin
θ
)
{\displaystyle E_{\text{kin}}={\tfrac {1}{2}}m({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}{\dot {\varphi }}^{2}\sin \theta )}
Allgemein
E
kin
=
1
2
m
|
v
→
|
2
{\displaystyle E_{\text{kin}}={\tfrac {1}{2}}m|{\vec {v}}|^{2}}
Potentielle Energie
Potentielle Energie an der Erdoberfläche:
E
pot
=
m
⋅
g
⋅
h
{\displaystyle E_{\text{pot}}=m\cdot g\cdot h}
mit:
g
:
{\displaystyle g\colon }
h
:
{\displaystyle h\colon }
Achtung: Dies ist keine allgemeine Formel für die potentielle Energie, sondern nur ein Spezialfall in der Nähe der Erdoberfläche.
Bei anderen Problemen sieht die potentielle Energie anders aus – zum Beispiel bei Molekülen, einer Feder, im Potential einer Ladung oder
im Gravitationspotential.
Einheiten
Energie
Masse
Schwerebeschleunigung
Höhe
[E ] = J
[m ] = kg
[g ] = N/kg = m/s2
[h ] = m
J: Joule, kg: Kilogramm, N: Newton, m: Meter, s: Sekunde
Spannenergie
Spannenergie einer Feder:
E
Spann
=
E
pot
=
1
2
D
⋅
s
2
{\displaystyle E_{\text{Spann}}=E_{\text{pot}}={\frac {1}{2}}\,D\cdot s^{2}}
mit:
D
{\displaystyle D}
s
:
{\displaystyle s\colon }
Spannenergie einer Drehfeder:
E
Spann
=
E
pot
=
1
2
D
⋅
φ
2
{\displaystyle E_{\text{Spann}}=E_{\text{pot}}={\frac {1}{2}}\,D\cdot \varphi ^{2}}
mit:
D
:
{\displaystyle D\colon }
φ
:
{\displaystyle \varphi \colon }
Einheiten
Energie
Federkonstante
Auslenkung
Direktionsmoment
Auslenkungswinkel
[E ] = J
[k ] = N/m
[s ] = m
[D ] = Nm
[φ ] = rad
J: Joule, N: Newton, m: Meter, rad: Radiant
Die Leistung
P
{\displaystyle P}
Δ
W
{\displaystyle \Delta W}
Δ
E
{\displaystyle \Delta E}
Δ
t
{\displaystyle \Delta t}
P
=
Δ
E
Δ
t
=
Δ
W
Δ
t
{\displaystyle P={\frac {\Delta E}{\Delta t}}={\frac {\Delta W}{\Delta t}}}
oder:
P
=
W
˙
=
F
→
⋅
d
s
→
d
t
=
F
→
⋅
v
→
.
{\displaystyle P={\dot {W}}={\vec {F}}\cdot {\frac {\mathrm {d} {\vec {s}}}{\mathrm {d} t}}={\vec {F}}\cdot {\vec {v}}.}
In einem Zeitintervall der Länge
T
=
[
t
1
,
t
2
]
{\displaystyle T=\left[t_{1},t_{2}\right]}
P
¯
:
{\displaystyle {\overline {P}}:}
P
¯
=
1
T
∫
t
1
t
2
P
(
t
)
d
t
.
{\displaystyle {\overline {P}}={\frac {1}{T}}\int _{t_{1}}^{t_{2}}P(t)\mathrm {d} t.}
Diese Angabe hat insbesondere Bedeutung, wenn
P
(
t
)
{\displaystyle P(t)}
T
{\displaystyle T}
η
=
W
abgegeben
W
zugeführt
⋅
100
%
=
E
abgegeben
E
zugeführt
⋅
100
%
=
P
abgegeben
P
zugeführt
⋅
100
%
<
1.
{\displaystyle \eta ={\frac {W_{\text{abgegeben}}}{W_{\text{zugeführt}}}}\cdot 100\%={\frac {E_{\text{abgegeben}}}{E_{\text{zugeführt}}}}\cdot 100\%={\frac {P_{\text{abgegeben}}}{P_{\text{zugeführt}}}}\cdot 100\%<1.}
Bei der Verkettung von Energie-umformenden Einrichtungen ist der Gesamtwirkungsgrad das Produkt der einzelnen Wirkungsgrade:
η
ges
=
η
1
⋅
η
2
⋅
…
⋅
η
n
.
{\displaystyle \eta _{\text{ges}}=\eta _{1}\cdot \eta _{2}\cdot \ldots \cdot \eta _{n}.}
Größe
Einheit
t : Zeits oder h
s : Wegm oder km
v : Geschwindigkeitm/s oder km/h
a : Beschleunigungm/s2
Einheiten
s: Sekunde, h: Stunde, m: Meter, km: Kilometer
Weg
Geschwindigkeit
Beschleunigung
s
=
v
⋅
(
t
−
t
0
)
+
s
0
{\displaystyle s=v\cdot (t-t_{0})+s_{0}}
v
=
v
0
=
s
−
s
0
t
−
t
0
{\displaystyle v=v_{0}={\frac {s-s_{0}}{t-t_{0}}}}
a
=
0
{\displaystyle a=0}
Weg
Geschwindigkeit
Beschleunigung
s
=
a
2
⋅
(
t
−
t
0
)
2
+
v
0
⋅
(
t
−
t
0
)
+
s
0
{\displaystyle s={\frac {a}{2}}\cdot (t-t_{0})^{2}+v_{0}\cdot (t-t_{0})+s_{0}}
v
=
a
⋅
(
t
−
t
0
)
+
v
0
{\displaystyle v=a\cdot (t-t_{0})+v_{0}}
a
=
a
0
=
v
−
v
0
t
−
t
0
{\displaystyle a=a_{0}={\frac {v-v_{0}}{t-t_{0}}}}
s
=
v
2
−
v
0
2
2
a
+
s
0
{\displaystyle s={\frac {v^{2}-v_{0}^{2}}{2a}}+s_{0}}
v
=
v
0
2
+
2
a
⋅
(
s
−
s
0
)
{\displaystyle v={\sqrt {v_{0}^{2}+2a\cdot (s-s_{0})}}}
a
=
v
2
−
v
0
2
2
(
s
−
s
0
)
{\displaystyle a={\frac {v^{2}-v_{0}^{2}}{2(s-s_{0})}}}
s
−
s
0
t
−
t
0
=
1
2
(
v
+
v
0
)
.
{\displaystyle {\frac {s-s_{0}}{t-t_{0}}}={\frac {1}{2}}(v+v_{0}).}
Weg
Geschwindigkeit
Beschleunigung
s
=
∫
t
0
t
v
d
t
+
s
0
{\displaystyle s=\int _{t_{0}}^{t}v\,\mathrm {d} t+s_{0}}
v
=
d
s
d
t
=
∫
t
0
t
a
d
t
+
v
0
{\displaystyle v={\frac {\mathrm {d} s}{\mathrm {d} t}}=\int _{t_{0}}^{t}a\,\mathrm {d} t+v_{0}}
a
=
d
v
d
t
{\displaystyle a={\frac {\mathrm {d} v}{\mathrm {d} t}}}
Definition. Gleichförmige Kreisbewegung.
Eine gleichförmige Kreisbewegung (gegen den Uhrzeigersinn) wird beschrieben durch:
r
→
(
t
)
:=
[
r
cos
(
φ
(
t
)
)
r
sin
(
φ
(
t
)
)
]
,
{\displaystyle {\vec {r}}(t):={\begin{bmatrix}r\cos(\varphi (t))\\r\sin(\varphi (t))\end{bmatrix}},}
φ
(
t
)
:=
ω
t
+
φ
0
.
{\displaystyle \varphi (t):=\omega t+\varphi _{0}.}
Die Parameter r , ω und φ 0 sind konstant.
r
→
(
t
)
{\displaystyle {\vec {r}}(t)}
Ortsvektor zum Zeitpunkt t
r
{\displaystyle r}
Radius
ω
{\displaystyle \omega }
Winkelgeschwindigkeit
φ
(
t
)
{\displaystyle \varphi (t)}
Winkel zum Zeitpunkt t
φ
0
{\displaystyle \varphi _{0}}
Anfangswinkel
T
{\displaystyle T}
Umlaufzeit
n
{\displaystyle n}
Drehzahl
Für die Winkelgeschwindigkeit gilt:
ω
=
Δ
φ
Δ
t
=
v
r
=
2
π
T
=
2
π
n
.
{\displaystyle \omega ={\frac {\Delta \varphi }{\Delta t}}={\frac {v}{r}}={\frac {2\pi }{T}}=2\pi n.}
Für die Beschleunigung gilt:
a
→
=
−
ω
2
r
→
.
{\displaystyle {\vec {a}}=-\omega ^{2}{\vec {r}}.}
Die Beschleunigung stimmt mit der Zentripetalbeschleunigung überein:
a
→
=
a
→
z
p
=
−
a
→
z
f
.
{\displaystyle {\vec {a}}={\vec {a}}_{\mathrm {zp} }=-{\vec {a}}_{\mathrm {zf} }.}
Betragsmäßige Gleichungen:
v
=
ω
r
,
{\displaystyle v=\omega r,}
a
z
p
=
ω
2
r
.
{\displaystyle a_{\mathrm {zp} }=\omega ^{2}r.}
Der Geschwindigkeitsvektor steht senkrecht zum Ortsvektor:
⟨
v
→
,
r
→
⟩
=
0.
{\displaystyle \langle {\vec {v}},{\vec {r}}\rangle =0.}
Der Beschleunigungsvektor steht senkrecht zum Geschwindigkeitsvektor:
⟨
a
→
,
v
→
⟩
=
0.
{\displaystyle \langle {\vec {a}},{\vec {v}}\rangle =0.}
Es gibt keine messbare Winkelbeschleunigung:
α
=
0.
{\displaystyle \alpha =0.}
Bearbeiten
Definition. Gleichmäßig beschleunigte Kreisbewegung.
Eine gleichmäßig beschleunigte Kreisbewegung (gegen den Uhrzeigersinn) wird beschrieben durch:
r
→
(
t
)
:=
[
r
cos
(
φ
(
t
)
)
r
sin
(
φ
(
t
)
)
]
,
{\displaystyle {\vec {r}}(t):={\begin{bmatrix}r\cos(\varphi (t))\\r\sin(\varphi (t))\end{bmatrix}},}
φ
(
t
)
:=
α
2
t
2
+
ω
0
t
+
φ
0
.
{\displaystyle \varphi (t):={\frac {\alpha }{2}}t^{2}+\omega _{0}t+\varphi _{0}.}
Die Parameter r , α , ω 0 und φ 0 sind konstant.
Es gilt
ω
=
α
t
+
ω
0
,
{\displaystyle \omega =\alpha t+\omega _{0},}
α
=
Δ
ω
Δ
t
{\displaystyle \alpha ={\frac {\Delta \omega }{\Delta t}}}
v
=
ω
r
{\displaystyle v=\omega r}
a
=
r
α
2
+
ω
4
{\displaystyle a=r{\sqrt {\alpha ^{2}+\omega ^{4}}}}
Für die Tangential- und die Zentripetalbeschleunigung gilt:
a
t
a
n
=
α
r
{\displaystyle a_{\mathrm {tan} }=\alpha r}
a
z
p
=
ω
2
r
{\displaystyle a_{\mathrm {zp} }=\omega ^{2}r}
Definition. Allgemeine Kreisbewegung.
Eine allgemeine Kreisbewegung (gegen den Uhrzeigersinn) wird beschrieben durch:
r
→
(
t
)
:=
[
r
cos
(
φ
(
t
)
)
r
sin
(
φ
(
t
)
)
]
,
{\displaystyle {\vec {r}}(t):={\begin{bmatrix}r\cos(\varphi (t))\\r\sin(\varphi (t))\end{bmatrix}},}
wobei φ (t ) ein zeitlich veränderlicher Winkel ist.
Definition. Winkelgeschwindigkeit.
Die Winkelgeschwindigkeit ist die Ableitung des Winkels nach der Zeit:
ω
=
d
φ
d
t
=
φ
′
(
t
)
.
{\displaystyle \omega ={\frac {\mathrm {d} \varphi }{\mathrm {d} t}}=\varphi '(t).}
Definition. Winkelbeschleunigung
Die Winkelbeschleunigung ist die Ableitung der Winkelgeschwindigkeit nach der Zeit:
α
=
d
ω
d
t
=
φ
″
(
t
)
.
{\displaystyle \alpha ={\frac {\mathrm {d} \omega }{\mathrm {d} t}}=\varphi ''(t).}
v
=
ω
r
{\displaystyle v=\omega r}
a
=
r
α
2
+
ω
4
{\displaystyle a=r{\sqrt {\alpha ^{2}+\omega ^{4}}}}
Für die Tangential- und die Zentripetalbeschleunigung gilt:
a
t
a
n
=
α
r
{\displaystyle a_{\mathrm {tan} }=\alpha r}
a
z
p
=
ω
2
r
{\displaystyle a_{\mathrm {zp} }=\omega ^{2}r}
a
2
=
a
t
a
n
2
+
a
z
p
2
.
{\displaystyle a^{2}=a_{\mathrm {tan} }^{2}+a_{\mathrm {zp} }^{2}.}
Die folgenden vektoriellen Beziehungen sind gültig:
v
→
=
ω
R
(
π
2
)
r
→
{\displaystyle {\vec {v}}=\omega R({\tfrac {\pi }{2}}){\vec {r}}}
a
→
t
a
n
=
α
R
(
π
2
)
r
→
{\displaystyle {\vec {a}}_{\mathrm {tan} }=\alpha R({\tfrac {\pi }{2}}){\vec {r}}}
a
→
z
p
=
−
ω
2
r
→
{\displaystyle {\vec {a}}_{\mathrm {zp} }=-\omega ^{2}{\vec {r}}}
a
→
=
a
→
t
a
n
+
a
→
z
p
{\displaystyle {\vec {a}}={\vec {a}}_{\mathrm {tan} }+{\vec {a}}_{\mathrm {zp} }}
Mit
R
(
π
2
)
=
[
0
−
1
1
0
]
{\displaystyle R({\tfrac {\pi }{2}})={\begin{bmatrix}0&-1\\1&0\end{bmatrix}}}
ist die Rotationsmatrix gemeint, die einen Vektor um 90° gegen den Uhrzeigersinn dreht.
Jeder Massepunkt der um eine feste Achse rotiert bewegt sich stets tangential. Um das Entfernen in diese Richtung zu verhindern bedarf es der Zentripetalkraft, welche Radial wirkt, also senkrecht zur Bewegungsrichtung, und so den Massepunkt auf eine Kreisbahn um die Achse zwingt.
Die Zentripetalkraft ist inertial und unterscheidet sich somit von der "Schein" -Zentrifugalkraft.
Für die Zentripetalkraft gilt:
F
→
z
p
:=
m
⋅
a
→
z
p
=
−
m
⋅
ω
2
⋅
r
→
,
{\displaystyle {\vec {F}}_{\mathrm {zp} }:=m\cdot {\vec {a}}_{\mathrm {zp} }=-m\cdot \omega ^{2}\cdot {\vec {r}},}
F
z
p
:=
|
F
→
z
p
|
=
m
⋅
ω
2
⋅
r
.
{\displaystyle F_{\mathrm {zp} }:=|{\vec {F}}_{\mathrm {zp} }|=m\cdot \omega ^{2}\cdot r.}
Die Zentrifugalkraft ist im Gegensatz zur Zentripetalkraft eine Scheinkraft, da sie nicht im inertialen äußeren Bezugssystem existiert sondern nur im relativen rotierenden System anscheinend in Erscheinung tritt. Wird ein um eine Achse rotierender Körper losgelassen, bewegt er sich im rotierenden Bezugssystem im ersten Moment Radial fort.
Für die Zentrifugalkraft gilt:
F
→
z
f
=
−
m
ω
→
×
(
ω
→
×
r
)
.
{\displaystyle {\vec {F}}_{\mathrm {zf} }=-m{\vec {\omega }}\times ({\vec {\omega }}\times r).}
Dabei ist
m
{\displaystyle m}
ω
→
{\displaystyle {\vec {\omega }}}
r
→
{\displaystyle {\vec {r}}}
Für den Spezialfall dass der Körper im rotierenden Bezugssystem ruht, ist die Zentrifugalkraft der Trägheitswiderstand in Bezug auf die Zentripetalkraft:
F
→
z
f
=
−
F
→
z
p
.
{\displaystyle {\vec {F}}_{\mathrm {zf} }=-{\vec {F}}_{\mathrm {zp} }.}
Dieser Trägheitswiderstand ist auch im Inertialsystem definiert.
Die folgenden Formeln beschreiben die Bewegung bei konstanter Beschleunigung.
Dies trifft zum Beispiel näherungsweise zu, wenn man Objekte in der Nähe der Erdoberfläche fallenläßt, entsprechend mit anderer Beschleunigung natürlich auch in der Nähe anderer großer Objekte wie Planeten, Monde, Sonnen etc.
g
{\displaystyle g}
h
{\displaystyle h}
ohne Reibung
Das ist der eigentliche freie Fall im Vakuum.
v
=
g
⋅
t
=
2
⋅
g
⋅
h
{\displaystyle v=g\cdot t={\sqrt {2\cdot g\cdot h}}}
t
=
2
⋅
h
g
{\displaystyle t={\sqrt {\frac {2\cdot h}{g}}}}
s
=
1
2
⋅
g
⋅
t
2
{\displaystyle s={\frac {1}{2}}\cdot g\cdot t^{2}}
mit Reibung
Reibung an sich ist ein recht komplexer Vorgang, bei dem Bewegungsenergie verloren geht, bezogen auf den freien Fall wird dies primär dadurch bewirkt, dass etwas durch die Luft fällt oder durch Wasser als Flüssigkeit.
Je nach Geschwindigkeit und Medium, durch welches die Bewegung führt, ist hat die Reibung andere Effekte.
Fall 1: Newton-Reibung
Dabei wird die Reibungskraft proportional zum Quadrat des Betrages der Geschwindigkeit relativ zum Medium angenommen.
Das tritt besonders bei hohen Geschwindigkeiten oder dichten Medien auf.
Im Falle von Gasen erzeugt das bewegte Objekt im Medium dabei meist Turbulenzen, die einen hohen Energieverlust bedeuten.
Bei Medien geringer Dichte oder kleinen Geschwindigkeiten wird dabei die Reibung eher zu klein abgeschätzt.
Momentanhöhe:
h
(
t
)
=
H
−
m
α
ln
[
cosh
(
α
g
m
⋅
t
)
]
{\displaystyle h(t)=H-{\frac {m}{\alpha }}\ln \left[\cosh \left({\sqrt {\frac {\alpha g}{m}}}\cdot t\right)\right]}
v
(
t
)
=
−
m
g
α
tanh
(
α
g
m
⋅
t
)
{\displaystyle v(t)=-{\sqrt {\frac {mg}{\alpha }}}\tanh \left({\sqrt {\frac {\alpha g}{m}}}\cdot t\right)}
a
(
t
)
=
−
g
cosh
2
(
α
g
m
⋅
t
)
{\displaystyle a(t)=-{\frac {g}{\cosh ^{2}\left({\sqrt {\frac {\alpha g}{m}}}\cdot t\right)}}}
Grenzgeschwindigkeit:
v
g
=
−
m
g
α
{\displaystyle v_{\mathrm {g} }=-{\sqrt {\frac {mg}{\alpha }}}}
Im Newton-Fall ist
α
=
1
2
⋅
c
w
ρ
A
{\displaystyle \alpha ={\tfrac {1}{2}}\cdot c_{\mathrm {w} }\,\rho \,A}
H
{\displaystyle H}
c
w
{\displaystyle c_{\mathrm {w} }}
Strömungswiderstandskoeffizient
ρ
{\displaystyle \rho }
Luftdichte
A
{\displaystyle A}
Stirnfläche des fallenden Körpers Fall 2: Stokes-Reibung
Bei Medien geringer Dichte oder kleinen Geschwindigkeiten wird dabei die Reibungskraft proportional zum Betrag der Geschwindigkeit abgeschätzt.
Bei hoher Dichte oder hoher Geschwindigkeit wird damit die Reibung als zu klein abgeschätzt.
h
(
t
)
=
H
+
m
α
g
[
m
α
(
1
−
e
−
(
α
/
m
)
t
)
−
t
]
{\displaystyle h(t)=H+{\frac {m}{\alpha }}g\left[{\frac {m}{\alpha }}\left(1-e^{-(\alpha /m)t}\right)-t\right]}
v
(
t
)
=
m
α
g
(
e
−
(
α
/
m
)
t
−
1
)
{\displaystyle v(t)={\frac {m}{\alpha }}g\left(e^{-(\alpha /m)t}-1\right)}
a
(
t
)
=
−
g
e
−
α
m
t
{\displaystyle a(t)=-g\,e^{-{\frac {\alpha }{m}}t}}
v
g
=
−
m
α
g
{\displaystyle v_{g}=-{\frac {m}{\alpha }}g}
Ort-Zeit-Gesetz
y
=
v
0
t
−
g
2
t
2
+
y
0
{\displaystyle y=v_{0}t-{\frac {g}{2}}t^{2}+y_{0}}
Geschwindigkeit-Zeit-Gesetz
v
=
v
0
−
g
t
{\displaystyle v=v_{0}-gt}
Ort-Geschwindigkeit-Gesetz
y
=
v
0
2
−
v
2
2
g
+
y
0
{\displaystyle y={\frac {v_{0}^{2}-v^{2}}{2g}}+y_{0}}
Steigzeit
t
u
=
v
0
g
{\displaystyle t_{u}={\frac {v_{0}}{g}}}
Gipfelpunkt
y
u
=
v
0
2
2
g
+
y
0
{\displaystyle y_{u}={\frac {v_{0}^{2}}{2g}}+y_{0}}
v
0
>
0
{\displaystyle v_{0}>0}
Wurf nach oben
v
0
<
0
{\displaystyle v_{0}<0}
Wurf nach unten
x
y
Ort-Zeit-Gesetz
x
=
x
0
+
v
0
t
{\displaystyle x=x_{0}+v_{0}t}
y
=
y
0
−
g
2
t
2
{\displaystyle y=y_{0}-{\frac {g}{2}}t^{2}}
Geschwindigkeit-Zeit-Gesetz
v
x
=
v
0
{\displaystyle v_{x}=v_{0}}
v
y
=
−
g
t
{\displaystyle v_{y}=-gt}
|
v
→
|
=
v
0
2
+
(
g
t
)
2
{\displaystyle |{\vec {v}}|={\sqrt {v_{0}^{2}+(gt)^{2}}}}
Wurfparabel
y
=
y
0
−
g
2
v
0
2
(
x
−
x
0
)
2
{\displaystyle y=y_{0}-{\frac {g}{2v_{0}^{2}}}(x-x_{0})^{2}}
x
y
Ort-Zeit-Gesetz
x
=
v
x
(
0
)
t
{\displaystyle x=v_{x}(0)\,t}
y
=
v
y
(
0
)
t
−
g
2
t
2
{\displaystyle y=v_{y}(0)\,t-{\frac {g}{2}}t^{2}}
Geschwindigkeit-Zeit-Gesetz
v
x
=
v
x
(
0
)
{\displaystyle v_{x}=v_{x}(0)}
v
y
=
v
y
(
0
)
−
g
t
{\displaystyle v_{y}=v_{y}(0)-gt}
Startgeschwindigkeit
v
x
(
0
)
=
v
0
cos
α
{\displaystyle v_{x}(0)=v_{0}\cos \alpha }
v
y
(
0
)
=
v
0
sin
α
{\displaystyle v_{y}(0)=v_{0}\sin \alpha }
v
0
:=
|
v
→
0
|
=
v
x
(
0
)
2
+
v
y
(
0
)
2
{\displaystyle v_{0}:=|{\vec {v}}_{0}|={\sqrt {v_{x}(0)^{2}+v_{y}(0)^{2}}}}
Ein kräftefreier Körper bleibt in Ruhe oder bewegt sich geradlinig mit konstanter Geschwindigkeit.
Eine auf einen Körper wirkende Kraft
F
→
{\displaystyle {\vec {F}}}
F
→
=
d
d
t
p
→
{\displaystyle {\vec {F}}={\frac {\mathrm {d} }{\mathrm {d} t}}\;{\vec {p}}}
Ist die Masse
m
{\displaystyle m}
F
→
=
m
d
d
t
v
→
=
m
⋅
a
→
{\displaystyle {\vec {F}}=m{\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {v}}=m\cdot {\vec {a}}}
Kraft gleich Gegenkraft : Eine Kraft von Körper A auf Körper B geht immer mit einer gleich großen, aber entgegen gerichteten Kraft von Körper B auf Körper A einher.
F
→
A
→
B
=
−
F
→
B
→
A
{\displaystyle {\vec {F}}_{A\to B}=-{\vec {F}}_{B\to A}}
Drehmoment = Kraft · Länge des Hebelarmes:
M
=
F
⋅
s
.
{\displaystyle M=F\cdot s.}
Einheit:
N
⋅
m
{\displaystyle \mathrm {N} \cdot \mathrm {m} }
Im Gleichgewicht gilt:
M
1
=
M
2
.
{\displaystyle M_{1}=M_{2}.}
Rechts drehendes Moment = Links drehendes Moment:
F
1
⋅
s
1
=
F
2
⋅
s
2
.
{\displaystyle F_{1}\cdot s_{1}=F_{2}\cdot s_{2}.}
Besteht der Flaschenzug aus n Rollen, so verteilt sich die Last ebenfalls auf n Seile. Im Falle des Gleichgewichts gilt:
Kraft = Last / Anzahl der Seile:
F
1
=
F
2
n
{\displaystyle F_{1}={\frac {F_{2}}{n}}}
wobei
F
1
{\displaystyle F_{1}}
F
2
{\displaystyle F_{2}}
Nomenklatur
F
→
G
{\displaystyle {\vec {F}}_{\mathrm {G} }}
Gewichtskraft
F
→
G
N
{\displaystyle {\vec {F}}_{\mathrm {GN} }}
Normalkomponente der Gewichtskraft
F
→
G
H
{\displaystyle {\vec {F}}_{\mathrm {GH} }}
Hangabtriebskomponente der Gewichtskraft
F
→
N
{\displaystyle {\vec {F}}_{\mathrm {N} }}
Normalkraft
F
→
R
{\displaystyle {\vec {F}}_{\mathrm {R} }}
Haftreibungskraft
μ
H
{\displaystyle \mu _{\mathrm {H} }}
Haftreibungskoeffizient
α
{\displaystyle \alpha }
Neigungswinkel
l
{\displaystyle l}
Länge
h
{\displaystyle h}
Höhe
b
{\displaystyle b}
Basis
b
=
l
cos
α
{\displaystyle b=l\cos \alpha }
F
G
N
=
F
G
cos
α
{\displaystyle F_{\mathrm {GN} }=F_{\mathrm {G} }\cos \alpha }
F
N
=
F
G
N
{\displaystyle F_{\mathrm {N} }=F_{\mathrm {GN} }}
h
=
l
sin
α
{\displaystyle h=l\sin \alpha }
F
G
H
=
F
G
sin
α
{\displaystyle F_{\mathrm {GH} }=F_{\mathrm {G} }\sin \alpha }
F
R
=
F
G
H
{\displaystyle F_{\mathrm {R} }=F_{\mathrm {GH} }}
Bedingung für die Ruhe eines haftenden Körpers:
F
R
≤
μ
H
⋅
F
N
bzw.
tan
α
≤
μ
H
.
{\displaystyle F_{\mathrm {R} }\leq \mu _{\mathrm {H} }\cdot F_{\mathrm {N} }\quad {\text{bzw.}}\quad \tan \alpha \leq \mu _{\mathrm {H} }.}
Reibungskraft = Reibungszahl · Normalkraft:
F
R
=
μ
⋅
F
N
.
{\displaystyle F_{R}=\mu \cdot F_{N}.}
Trockene Reibung (Gleitreibung):
F
→
R
T
=
−
α
T
.
{\displaystyle {\vec {F}}_{\mathrm {RT} }=-\alpha _{\mathrm {T} }.}
Für den Impuls gilt:
p
→
=
m
⋅
v
→
{\displaystyle {\vec {p}}=m\cdot {\vec {v}}}
E
kinetisch
=
p
→
2
2
m
{\displaystyle E_{\text{kinetisch}}={\frac {{\vec {p}}^{2}}{2\ m}}}
Δ
p
→
=
m
⋅
Δ
v
→
=
∫
t
1
t
2
F
→
(
t
)
d
t
{\displaystyle \Delta {\vec {p}}=m\cdot \Delta {\vec {v}}=\int _{t_{1}}^{t_{2}}{\vec {F}}(t)\mathrm {d} t}
d
p
→
d
t
=
F
→
.
{\displaystyle {\frac {\mathrm {d} {\vec {p}}}{\mathrm {d} t}}={\vec {F}}.}
Impulse bleiben (in einem kräftemäßig abgeschlossenen System) in der Summe erhalten.
Für den Kraftstoß gilt:
I
→
=
F
→
⋅
Δ
t
bei
F
→
=
konstant
{\displaystyle {\vec {I}}={\vec {F}}\cdot \Delta t\qquad {\text{bei }}{\vec {F}}={\text{konstant}}}
I
→
=
Δ
p
→
=
∫
F
→
(
t
)
⋅
d
t
.
{\displaystyle {\vec {I}}=\Delta {\vec {p}}=\int {\vec {F}}(t)\cdot \mathrm {d} t.}
Für den Drehimpuls gilt:
L
→
=
J
⋅
ω
→
{\displaystyle {\vec {L}}=J\cdot {\vec {\omega }}}
und außerdem:
d
L
→
d
t
=
M
→
{\displaystyle {\frac {\mathrm {d} {\vec {L}}}{\mathrm {d} t}}={\vec {M}}}
mit:
L
{\displaystyle L}
J
{\displaystyle J}
ω
{\displaystyle \omega }
M
{\displaystyle M}
Der Gesamtdrehimpuls eines isolierten physikalischen Systems bleibt unverändert.
Geschwindigkeiten vor dem Stoß:
v
1
,
v
2
.
{\displaystyle v_{1},v_{2}.}
Geschwindigkeiten nach dem Stoß:
u
,
u
1
,
u
2
.
{\displaystyle u,u_{1},u_{2}.}
Impulserhaltung:
m
1
⋅
v
1
+
m
2
⋅
v
2
=
m
1
⋅
u
1
+
m
2
⋅
u
2
.
{\displaystyle m_{1}\cdot v_{1}+m_{2}\cdot v_{2}=m_{1}\cdot u_{1}+m_{2}\cdot u_{2}.}
Energieerhaltung:
1
2
m
1
⋅
v
1
2
+
1
2
m
2
⋅
v
2
2
=
1
2
m
1
⋅
u
1
2
+
1
2
m
2
⋅
u
2
2
.
{\displaystyle {\frac {1}{2}}m_{1}\cdot v_{1}^{2}+{\frac {1}{2}}m_{2}\cdot v_{2}^{2}={\frac {1}{2}}m_{1}\cdot u_{1}^{2}+{\frac {1}{2}}m_{2}\cdot u_{2}^{2}.}
Geschwindigkeiten nach dem Stoß:
u
1
=
m
1
⋅
v
1
+
m
2
⋅
(
2
v
2
−
v
1
)
m
1
+
m
2
.
{\displaystyle u_{1}={\frac {m_{1}\cdot v_{1}+m_{2}\cdot (2\ v_{2}-v_{1})}{m_{1}+m_{2}}}.}
u
2
=
m
2
⋅
v
2
+
m
1
⋅
(
2
v
1
−
v
2
)
m
1
+
m
2
.
{\displaystyle u_{2}={\frac {m_{2}\cdot v_{2}+m_{1}\cdot (2\ v_{1}-v_{2})}{m_{1}+m_{2}}}.}
Spezialfall: bei gleichen Massen:
u
1
=
v
2
u
2
=
v
1
.
{\displaystyle u_{1}=v_{2}\qquad u_{2}=v_{1}.}
Impulserhaltung:
m
1
⋅
v
1
+
m
2
⋅
v
2
=
(
m
1
+
m
2
)
⋅
u
.
{\displaystyle m_{1}\cdot v_{1}+m_{2}\cdot v_{2}=(m_{1}+m_{2})\cdot u.}
Verringerung der kinetischen Energie (Verformungsenergie):
1
2
(
m
1
⋅
v
1
2
+
m
2
⋅
v
2
2
)
−
1
2
(
m
1
+
m
2
)
⋅
u
2
.
{\displaystyle {\frac {1}{2}}(m_{1}\cdot v_{1}^{2}+m_{2}\cdot v_{2}^{2})-{\frac {1}{2}}(m_{1}+m_{2})\cdot u^{2}.}
Geschwindigkeit
u
{\displaystyle u}
u
=
m
1
⋅
v
1
+
m
2
⋅
v
2
m
1
+
m
2
.
{\displaystyle u={\frac {m_{1}\cdot v_{1}+m_{2}\cdot v_{2}}{m_{1}+m_{2}}}.}
Änderung der Bewegungsenergie ("Verlust"):
Δ
E
=
(
E
kin.vor
−
E
kin.nach
)
⋅
(
1
−
k
2
)
=
1
2
(
1
−
k
2
)
⋅
m
1
⋅
m
2
m
1
+
m
2
⋅
(
v
1
−
v
2
)
2
.
{\displaystyle \Delta E=(E_{\text{kin.vor}}-E_{\text{kin.nach}})\cdot (1-k^{2})={\frac {1}{2}}(1-k^{2})\cdot {\frac {m_{1}\cdot m_{2}}{m_{1}+m_{2}}}\cdot (v_{1}-v_{2})^{2}.}
Stoßzahl:
k
=
u
2
−
u
1
v
1
−
v
2
.
{\displaystyle k={\frac {u_{2}-u_{1}}{v_{1}-v_{2}}}.}
Außerdem gilt:
u
1
=
v
1
⋅
(
m
1
−
k
⋅
m
2
)
+
v
2
⋅
(
1
+
k
)
⋅
m
2
m
1
+
m
2
.
{\displaystyle u_{1}={\frac {v_{1}\cdot (m_{1}-k\cdot m_{2})+v_{2}\cdot (1+k)\cdot m_{2}}{m_{1}+m_{2}}}.}
u
2
=
v
2
⋅
(
m
2
−
k
⋅
m
1
)
+
v
1
⋅
(
1
+
k
)
⋅
m
1
m
1
+
m
2
.
{\displaystyle u_{2}={\frac {v_{2}\cdot (m_{2}-k\cdot m_{1})+v_{1}\cdot (1+k)\cdot m_{1}}{m_{1}+m_{2}}}.}
Dichte = Masse / Volumen:
ρ
=
m
V
.
{\displaystyle \rho ={\frac {m}{V}}.}
Druck = senkrecht wirkende Kraft / Fläche:
p
=
|
F
→
⊥
|
|
A
→
|
.
{\displaystyle p={\frac {|{\vec {F}}_{\perp }|}{|{\vec {A}}|}}.}
Einheit: Pa (Pascal)}
Schweredruck:
p
=
F
G
A
=
m
⋅
g
A
=
ρ
⋅
h
⋅
g
.
{\displaystyle p={\frac {F_{G}}{A}}={\frac {m\cdot g}{A}}=\rho \cdot h\cdot g.}
Auftriebskraft:
F
A
=
ρ
⋅
V
⋅
g
.
{\displaystyle F_{A}=\rho \cdot V\cdot g.}
(siehe Link)
Definition. Gibt es ein (auf einer offenen Teilmenge des euklidischen Raumes definiertes,
stetig differenzierbares) Skalarfeld
U
(
r
→
)
{\displaystyle U({\vec {r}})}
F
→
(
r
→
)
=
−
∇
U
(
r
→
)
,
{\displaystyle {\vec {F}}({\vec {r}})=-\nabla U({\vec {r}}),}
so nennt man
F
→
{\displaystyle {\vec {F}}}
U
{\displaystyle U}
k
{\displaystyle k}
E
pot
(
r
→
)
=
k
⋅
U
(
r
→
)
.
{\displaystyle E_{\text{pot}}({\vec {r}})=k\cdot U({\vec {r}}).}
Triviale Eichfreiheit: Das Potential ist nur bis auf eine additive Konstante bestimmt.
Potentialfelder sind Rotationsfrei:
∇
×
F
→
=
0.
{\displaystyle \nabla \times {\vec {F}}=0.}
Die Arbeit im Potentialfeld ist wegunabhängig:
W
=
−
∫
γ
⟨
∇
U
(
r
→
)
,
d
r
→
⟩
=
U
(
r
→
1
)
−
U
(
r
→
2
)
,
{\displaystyle W=-\int _{\gamma }\langle \nabla U({\vec {r}}),\mathrm {d} {\vec {r}}\rangle =U({\vec {r}}_{1})-U({\vec {r}}_{2}),}
wobei
U
=
E
p
o
t
{\displaystyle U=E_{\mathrm {pot} }}
γ
(
t
)
=
r
→
(
t
)
{\displaystyle \gamma (t)={\vec {r}}(t)}
γ
(
0
)
=
r
→
1
{\displaystyle \gamma (0)={\vec {r}}_{1}}
γ
(
1
)
=
r
→
2
{\displaystyle \gamma (1)={\vec {r}}_{2}}
W
<
0
{\displaystyle W<0}
Arbeit muss aufgebracht werden
W
>
0
{\displaystyle W>0}
Arbeit wird freigegeben
Einer Punktmasse, die sich auf der Parameterkurve
r
→
(
t
)
{\displaystyle {\vec {r}}(t)}
t die kinetische Energie
E
kin
(
t
)
=
1
2
m
|
v
→
(
t
)
|
2
=
1
2
m
|
r
→
′
(
t
)
|
2
{\displaystyle E_{\text{kin}}(t)={\tfrac {1}{2}}m|{\vec {v}}(t)|^{2}={\tfrac {1}{2}}m|{\vec {r}}'(t)|^{2}}
zugeordnet. Befindet sich die Punktmasse in einem Potentialfeld, so besitzt sie am Ort
r
→
{\displaystyle {\vec {r}}}
E
pot
(
r
→
)
.
{\displaystyle E_{\text{pot}}({\vec {r}}).}
Bei der Bewegung der Punktmasse im Potentialfeld gilt:
d
d
t
E
kin
(
t
)
+
d
d
t
E
pot
(
r
→
(
t
)
)
=
0.
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}E_{\text{kin}}(t)+{\frac {\mathrm {d} }{\mathrm {d} t}}E_{\text{pot}}({\vec {r}}(t))=0.}
Nach Integration bekommt die Gleichung die Gestalt:
E
kin
(
t
1
)
+
E
pot
(
r
→
(
t
1
)
)
=
E
kin
(
t
2
)
+
E
pot
(
r
→
(
t
2
)
)
.
{\displaystyle E_{\text{kin}}(t_{1})+E_{\text{pot}}({\vec {r}}(t_{1}))=E_{\text{kin}}(t_{2})+E_{\text{pot}}({\vec {r}}(t_{2})).}
In Kurzschreibweise:
T 1 +V 1 = T 2 +V 2 mit T =E kin und V =E pot .
In Worten:
Die Summe aus kinetischer und potentieller Energie ist die Gesamtenergie einer Punktmasse in einem Potentialfeld. Die Gesamtenergie ist konstant, sie hat zu jedem Zeitpunkt den selben Wert.
Potential
Potentielle Energie
Potentialfeld
Höhenpotential
U
(
h
)
=
m
g
h
{\displaystyle U(h)=mgh}
E
pot
=
U
(
h
)
{\displaystyle E_{\text{pot}}=U(h)}
F
(
h
)
=
−
∇
U
(
h
)
=
−
m
g
{\displaystyle F(h)=-\nabla U(h)=-mg}
Potential einer Feder
U
(
s
)
=
1
2
D
s
2
{\displaystyle U(s)={\tfrac {1}{2}}Ds^{2}}
E
pot
=
U
(
s
)
{\displaystyle E_{\text{pot}}=U(s)}
F
(
s
)
=
−
∇
U
(
s
)
=
−
D
s
{\displaystyle F(s)=-\nabla U(s)=-Ds}
Gravitationspotential einer kugelförmigen Masse
M
{\displaystyle M}
U
(
r
→
)
=
−
G
M
|
r
→
|
{\displaystyle U({\vec {r}})=-{\frac {GM}{|{\vec {r}}|}}}
E
pot
=
m
U
(
r
→
)
{\displaystyle E_{\text{pot}}=mU({\vec {r}})}
g
→
(
r
→
)
=
−
∇
U
(
r
→
)
=
−
G
M
r
→
|
r
→
|
3
{\displaystyle {\vec {g}}({\vec {r}})=-\nabla U({\vec {r}})=-GM{\frac {\vec {r}}{|{\vec {r}}|^{3}}}}
Elektrisches Potential einer Ladung
Q
{\displaystyle Q}
U
(
r
→
)
=
Q
4
π
ε
0
|
r
→
|
{\displaystyle U({\vec {r}})={\frac {Q}{4\pi \varepsilon _{0}|{\vec {r}}|}}}
E
pot
=
q
U
(
r
→
)
{\displaystyle E_{\text{pot}}=qU({\vec {r}})}
E
→
(
r
→
)
=
−
∇
U
(
r
→
)
=
Q
r
→
4
π
ϵ
0
|
r
→
|
3
{\displaystyle {\vec {E}}({\vec {r}})=-\nabla U({\vec {r}})={\frac {Q{\vec {r}}}{4\pi \epsilon _{0}|{\vec {r}}|^{3}}}}
Das Gravitationsgesetz lautet:
F
→
=
G
⋅
m
1
⋅
m
2
r
2
{\displaystyle {\vec {F}}=G\cdot {\frac {m_{1}\cdot m_{2}}{r^{2}}}}
Für die Hubarbeit im Gravitationsfeld ergibt sich:
W
H
=
F
G
⋅
h
.
{\displaystyle W_{H}=F_{G}\cdot h.}
Daraus folgt:
W
H
=
G
⋅
M
⋅
m
r
2
⋅
h
{\displaystyle W_{H}=G\cdot {\frac {M\cdot m}{r^{2}}}\cdot h}
oder:
W
H
=
m
⋅
G
⋅
M
r
2
⋅
h
{\displaystyle W_{H}=m\cdot {\frac {G\cdot M}{r^{2}}}\cdot h}
oder:
W
H
=
m
⋅
g
⋅
h
.
{\displaystyle W_{H}=m\cdot g\cdot h.}
Für die potentielle Energie in einem Gravitationsfeld gilt:
E
p
o
t
=
−
G
⋅
m
1
⋅
m
2
r
{\displaystyle E_{\mathrm {pot} }=-G\cdot {\frac {m_{1}\cdot m_{2}}{r}}}
mit:
Gravitationskraft
F
{\displaystyle F}
Massen der sich anziehenden Körper:
m
1
{\displaystyle m_{1}}
m
2
{\displaystyle m_{2}}
Abstand der sich anziehenden Körper:
r
{\displaystyle r}
Richtung zwischen den sich anziehenden Körpern:
e
→
r
{\displaystyle {\vec {e}}_{r}}
Gravitationskonstante:
G
=
(
6,674
2
±
0,001
0
)
⋅
10
−
11
m
3
k
g
s
2
{\displaystyle G=(6{,}6742\pm 0{,}0010)\cdot 10^{-11}\;\mathrm {\frac {m^{3}}{kg\,s^{2}}} }
Auf der Erde gilt:
Kraft = Masse · Erdbeschleunigung
F
=
m
⋅
g
{\displaystyle F=m\cdot g}
Die Erdbeschleunigung g hängt von der geografischen Breite und der Höhe über Meeresniveau ab und ist am Äquator ca. g = 9,780 m/s² und an den Polen ca. g = 9,832 m/s².
Erdbeschleunigung:
g
=
G
⋅
M
r
2
{\displaystyle g={\frac {G\cdot M}{r^{2}}}}
mit
Erdmasse:
M
=
5,972
⋅
10
24
k
g
{\displaystyle M=5{,}972\cdot 10^{24}\,\mathrm {kg} }
Erdradius:
r
=
6371
k
m
{\displaystyle r=6371\,\mathrm {km} }
Gravitationskonstante:
G
=
6,674
⋅
10
−
11
m
3
k
g
s
2
{\displaystyle G=6{,}674\cdot 10^{-11}\,{\frac {\mathrm {m^{3}} }{\mathrm {kg\,s^{2}} }}}
Diese Formel liefert etwa 9,82 m/s².
1. kosmische Geschwindigkeit (Kreisbahngeschwindigkeit)
Die 1. kosmologische Geschwindigkeit berechnet sich wie folgt:
v
K
=
G
⋅
M
r
{\displaystyle v_{K}={\sqrt {\frac {G\cdot M}{r}}}}
M
{\displaystyle M}
r
{\displaystyle r}
v
K, Erde
=
7
,
9
k
m
s
{\displaystyle v_{\text{K, Erde}}=7{,}9\,\mathrm {\frac {km}{s}} }
Herleitung :
Bei einer Kreisbewegung eines Probekörpers
m
{\displaystyle m}
M
{\displaystyle M}
F
Z
f
{\displaystyle F_{Zf}}
F
G
{\displaystyle F_{G}}
Zentrifugalkraft
F
Z
f
{\displaystyle F_{Zf}}
F
G
{\displaystyle F_{G}}
Daraus folgt:
v
2
⋅
m
r
=
G
⋅
M
⋅
m
r
2
{\displaystyle {\frac {v^{2}\cdot m}{r}}={\frac {G\cdot M\cdot m}{r^{2}}}}
Umstellen nach
v
{\displaystyle v}
v
=
G
⋅
M
r
{\displaystyle v={\sqrt {\frac {G\cdot M}{r}}}}
2. kosmische Geschwindigkeit (Fluchtgeschwindigkeit)
Die 2. kosmologische Geschwindigkeit berechnet sich wie folgt:
v
F
=
2
⋅
G
⋅
M
r
{\displaystyle v_{F}={\sqrt {\frac {\,2\cdot G\cdot M}{r}}}}
v
F, Erde
=
11
,
2
k
m
s
{\displaystyle v_{\text{F, Erde}}=11{,}2\,\mathrm {\frac {km}{s}} }
Herleitung:
Bei der minimalen Fluchtgeschwindigkeit ist die kinetische Energie eines Probekörpers gerade gleich der Gravitationsenergie .
Kinetische Energie
E
kin
{\displaystyle E_{\text{kin}}}
E
G
{\displaystyle E_{G}}
Daraus folgt:
1
2
⋅
m
⋅
v
2
=
G
⋅
M
⋅
m
r
{\displaystyle {\frac {1}{2}}\cdot m\cdot v^{2}=G\cdot {\frac {M\cdot m}{r}}}
Umstellen nach
v
{\displaystyle v}
v
=
2
⋅
G
⋅
M
r
.
{\displaystyle v={\sqrt {\frac {2\cdot G\cdot M}{r}}}.}
Definition. Federkraft = Federkonstante · Federverlängerung:
F
=
D
⋅
Δ
l
{\displaystyle F=D\cdot \Delta l}
oder:
F
=
D
⋅
s
.
{\displaystyle F=D\cdot s.}
Es ist zu beachten, dass die Rückstellkraft die entgegengesetzte Richtung wie die Verlängerung hat (Feder wird wieder kürzer).
Für eine Verlängerung müsste ein Minus [-] eingefügt werden, um die Richtung miteinzubeziehen:
F
=
−
D
⋅
s
.
{\displaystyle F=-D\cdot s.}
Für die Spannarbeit an einer Feder ergibt sich:
W
Spann
=
1
2
D
⋅
s
2
.
{\displaystyle W_{\text{Spann}}={\frac {1}{2}}\ D\cdot s^{2}.}
Spannenergie einer Feder:
E
Spann
=
E
pot
=
1
2
D
⋅
s
2
{\displaystyle E_{\text{Spann}}=E_{\text{pot}}={\frac {1}{2}}\,D\cdot s^{2}}
mit:
D
{\displaystyle D}
s
:
{\displaystyle s\colon }
Spannenergie einer Drehfeder:
E
Spann
=
E
pot
=
1
2
D
⋅
φ
2
{\displaystyle E_{\text{Spann}}=E_{\text{pot}}={\frac {1}{2}}\,D\ \cdot \varphi ^{2}}
mit:
D
:
{\displaystyle D\colon }
φ
:
{\displaystyle \varphi \colon }
Hookesches Gesetz für den einachsigen Spannungszustand:
σ
=
E
⋅
ε
.
{\displaystyle \sigma =E\cdot \varepsilon .}
Daraus folgt das E-Modul:
E
=
σ
ε
{\displaystyle E={\frac {\sigma }{\varepsilon }}}
oder für die Verzerrung:
ε
=
σ
E
{\displaystyle \varepsilon ={\frac {\sigma }{E}}}
wobei:
σ
{\displaystyle \sigma }
Spannung (Kraft pro Fläche)
ε
{\displaystyle \varepsilon }
Verzerrung (Längenänderung durch ursprüngliche Länge)
E
{\displaystyle E}
Elastizitätsmodul (auch Zugmodul, Elastizitätskoeffizient, Dehnungsmodul, E.Modul usw.).Verzerrungstensor
Der Verzerrungstensor lautet:
ε
i
j
:=
1
2
(
∂
u
i
∂
x
j
+
∂
u
j
∂
x
i
)
,
{\displaystyle \varepsilon _{ij}:={\frac {1}{2}}\left({\frac {\partial u_{i}}{\partial x_{j}}}+{\frac {\partial u_{j}}{\partial x_{i}}}\right),}
wobei:
u
→
=
(
u
i
)
i
∈
{
1
,
2
,
3
}
{\displaystyle {\vec {u}}=\left(u_{i}\right)_{i\in \{1,2,3\}}}
Der Verzerrungstensor ist symmetrisch:
ε
i
j
=
ε
j
i
.
{\displaystyle \varepsilon _{ij}=\varepsilon _{ji}.}
Spannungstensor
(siehe Link)
Tensorielle Form des Hookschen Gesetzes
Die tensorielle Form des Hookeschen Gesetzes lautet:
σ
i
j
=
∑
k
l
c
i
j
k
l
⋅
ε
k
l
.
{\displaystyle \sigma _{ij}=\sum _{kl}c_{ijkl}\cdot \varepsilon _{kl}.}
Für die Spannung bei einem Stab der Länge
l
0
{\displaystyle l_{0}}
σ
x
=
F
x
A
{\displaystyle \sigma _{x}={\frac {F_{x}}{A}}}
mit:
F
x
:
{\displaystyle F_{x}:}
A
:
{\displaystyle A:}
Für die Dehung eines Stabes in x-Richtung ergibt sich:
ε
=
Δ
l
l
0
.
{\displaystyle \varepsilon ={\frac {\Delta l}{l_{0}}}.}
Das Hookesche Gesetz lautete:
σ
=
E
⋅
ε
.
{\displaystyle \sigma =E\cdot \varepsilon .}
Durch Einsetzen und Umstellen erhält mann:
F
x
=
E
⋅
A
⋅
Δ
l
l
0
.
{\displaystyle F_{x}=E\cdot A\cdot {\frac {\Delta l}{l_{0}}}.}
Dieses erweitere Hookesche Gesetz lässt sich dort anwenden, wo die wirkende Kraft nahezu linear von der Ausdehnung bzw. Auslenkung abhängt, und ist eine Verallgemeinerung des Hookeschen Gesetzes für Federn.
Parallelschaltung
Für die Parallelschaltung von Federn ergibt sich:
D
=
D
1
+
D
2
+
D
3
+
⋯
+
D
n
=
∑
i
=
1
n
D
i
.
{\displaystyle D=D_{1}+D_{2}+D_{3}+\dots +D_{n}=\sum _{i=1}^{n}D_{i}.}
Reihenschaltung
Für die Reihenschaltung von Federn ergibt sich:
1
D
=
1
D
1
+
1
D
2
+
1
D
3
+
⋯
+
1
D
n
=
∑
i
=
1
n
1
D
i
.
{\displaystyle {\frac {1}{D}}={\frac {1}{D_{1}}}+{\frac {1}{D_{2}}}+{\frac {1}{D_{3}}}+\dots +{\frac {1}{D_{n}}}=\sum _{i=1}^{n}{\frac {1}{D_{i}}}.}
Federschaltungen verhalten sich in diesem Sinne wie Kondensatorschaltungen.
Jede Feder kann sich jedoch nur bis zu einem bestimmten Punkt ausdehnen.
(siehe Link)
Weg-Zeit-Gesetz des Federpendels :
s
(
t
)
=
s
^
⋅
cos
ω
t
{\displaystyle s(t)={\hat {s}}\cdot \cos \omega t}
Geschwindigkeits-Zeit-Gesetz des Federpendels :
v
(
t
)
=
−
ω
s
^
⋅
sin
ω
t
{\displaystyle v(t)=-\omega {\hat {s}}\cdot \sin \omega t}
Beschleunigungs-Zeit-Gesetz des Federpendels :
a
(
t
)
=
−
ω
2
s
^
⋅
cos
ω
t
{\displaystyle a(t)=-\omega ^{2}{\hat {s}}\cdot \cos \omega t}
Frequenz des Federpendels :
f
=
1
2
π
D
m
{\displaystyle f={\frac {1}{2\pi }}{\sqrt {\frac {D}{m}}}}
Schwingungsdauer des Federpendels :
T
=
2
π
m
D
{\displaystyle T=2\pi {\sqrt {\frac {m}{D}}}}
(siehe Link)
(siehe Link)
(siehe Link)
Die Hydrostatik ist die Lehre von den ruhenden Flüssigkeiten und den sich in ihnen ausbildenden
Kräften unter der Wirkung äußerer Kräfte. Aufgabe der Hydrostatik ist es, die infolge des hydrostatischen
Drucks auftretenden Erscheinungen zu analysieren und Kraftwirkungen zu ermitteln.
Bearbeiten
Unter dem hydraulischen Druck p versteht man den Quotienten aus Normalkraft und gedrückter Fläche:
Der Druck ist eine skalare Größe, d. h., er ist in einem Punkt eines Fluids ( Flüssigkeit, Gas, Dampf )
nach allen Richtungen gleich groß. Zur Angabe seiner Größe genügt demnach eine einzige Zahlenangabe
mit dazugehöriger Einheit.
Die Einheit des Druckes ist das Pascal ( Pa ). 1 Pa ist der Druck, der durch eine Kraft von 1 N erzeugt
wird, welche gleichmäßig auf die zu ihr senkrechten Fläche von 1 m² wirkt:
1 Pa = 1 N/m² = 1 kg/( m * s² )
1 bar = 1000 mbar = 105 Pa = 103 hPa ( Hektopascal )
Druck p am Boden eines Fluides in Tiefe h ergibt
Beachte:
1) h wird nach unten von der Fluidoberfläche gezählt
2) der Druck nimmt linear mit der Tiefe zu
3) der Druck ist isotrop, d.h. er wirkt in einer Tiefe h in alle Richtungen gleich
Beispiel 2.1.1: Wasserdruck in 10 m Tiefe
Gegeben: h = 10 m; Dichte des Wassers
ρ
{\displaystyle \rho }
Gesucht: Wasserdruck p
Lösung: p =
ρ
{\displaystyle \rho }
Die Wellengeschwindigkeit ist hier mit c bezeichnet. Für eine elektromagnetische Welle ist diese die Lichtgeschwindigkeit.
Ψ
{\displaystyle \Psi \,}
Zusammenhang von Frequenz
f
{\displaystyle f\ }
λ
{\displaystyle \lambda \ }
λ
=
c
f
{\displaystyle \lambda ={\frac {c}{f}}}
f
=
c
λ
{\displaystyle f={\frac {c}{\lambda }}}
gelegentlich wird auch der Buchstabe
ν
{\displaystyle \nu }
f
{\displaystyle f}
Intensitätsverlauf :
I
(
Θ
)
=
I
0
(
sin
(
π
b
λ
sin
θ
)
π
b
λ
sin
θ
)
2
{\displaystyle I(\Theta )=I_{0}\left({\frac {\sin \left({\frac {\pi b}{\lambda }}\sin \theta \right)}{{\frac {\pi b}{\lambda }}\sin \theta }}\right)^{2}}
Konstruktive Interferenz (Maximum) :
b
sin
Θ
=
±
(
n
+
1
2
)
λ
{\displaystyle b\sin \Theta =\pm \left(n+{\frac {1}{2}}\right)\lambda }
Destruktive Interferenz (Minimum) :
b
sin
Θ
=
±
n
λ
{\displaystyle b\sin \Theta =\pm n\lambda \,}
wobei
n eine positive Ganzahl ist (1, 2, 3, …) (Null ist ausgenommen ). Sie wird auch die Ordnung des Maximums bzw. Minimums genannt.
λ
{\displaystyle \lambda }
Wellenlänge
b
{\displaystyle b}
I
0
=
I
(
Θ
=
0
)
{\displaystyle I_{0}=I(\Theta =0)}
Θ
{\displaystyle \Theta \;}
Achtung :
Die Formeln für Minimum und Maximum gelten nur für positive Ganzzahlen. Bei
Θ
=
0
{\displaystyle \Theta =0}
Konstruktive Interferenz (Maximum) :
a
sin
Θ
=
n
λ
{\displaystyle a\sin \Theta =n\lambda \;}
Destruktive Interferenz (Minimum) :
a
sin
Θ
=
λ
(
n
+
1
2
)
{\displaystyle a\sin \Theta =\lambda \left(n+{\frac {1}{2}}\right)\,}
Intensitätsverlauf :
I
(
Θ
)
=
I
0
(
sin
(
π
b
λ
sin
Θ
)
π
b
λ
sin
Θ
)
2
cos
2
(
a
π
λ
sin
Θ
)
{\displaystyle I(\Theta )=I_{0}\left({\frac {\sin \left({\frac {\pi b}{\lambda }}\sin \Theta \right)}{{\frac {\pi b}{\lambda }}\sin \Theta }}\right)^{2}\cos ^{2}\left({\frac {a\pi }{\lambda }}\sin \Theta \right)}
Intensitätsverlauf für
b
≪
λ
{\displaystyle b\ll \lambda }
:
I
(
Θ
)
=
cos
2
(
a
π
λ
sin
Θ
)
{\displaystyle I(\Theta )=\cos ^{2}\left({\frac {a\pi }{\lambda }}\sin \Theta \right)}
wobei
n eine Ganzzahl ist. Sie wird auch die Ordnung des Maximums bzw. Minimums genannt.
λ
{\displaystyle \lambda }
Wellenlänge ist
a
{\displaystyle a}
b
{\displaystyle b}
I
0
=
I
(
Θ
=
0
)
{\displaystyle I_{0}=I(\Theta =0)}
Θ
{\displaystyle \Theta \;}
Beugung an einem Gitter mit 6 Spalten Intensitätsverlauf :
I
(
Θ
)
=
I
0
(
sin
(
π
b
λ
sin
Θ
)
π
b
λ
sin
Θ
)
2
(
sin
(
π
N
g
λ
sin
Θ
)
π
g
λ
sin
Θ
)
2
{\displaystyle I(\Theta )=I_{0}\left({\frac {\sin \left({\frac {\pi b}{\lambda }}\sin \Theta \right)}{{\frac {\pi b}{\lambda }}\sin \Theta }}\right)^{2}\left({\frac {\sin \left({\frac {\pi Ng}{\lambda }}\sin \Theta \right)}{{\frac {\pi g}{\lambda }}\sin \Theta }}\right)^{2}}
Hauptmaxima :
g
sin
Θ
=
n
λ
{\displaystyle g\sin \Theta =n\lambda \ }
Zwischen zwei Hauptmaxima liegen immer n-1 Nebenminima und n-2 Nebenmaxima.
wobei
n eine Ganzahl ist. Sie wird auch die Ordnung des Maximums genannt.
λ
{\displaystyle \lambda }
Wellenlänge
b
{\displaystyle b}
N
{\displaystyle N}
g
{\displaystyle g}
Gitterparameter (Abstand zweier Spalte des Gitters)
I
0
=
I
(
Θ
=
0
)
{\displaystyle I_{0}=I(\Theta =0)}
Θ
{\displaystyle \Theta \;}
Divergente Strahlen : Strahlen, die von einem Punkt ausgehen (wie bei der auslaufenden Kugelwelle)Konvergente Strahlen : Strahlen, die in einem Punkt zusammenlaufen (wie bei der einlaufenden Kugelwelle)Parallele Strahlen : alle Strahlen verlaufen parallel zueinander. Dies entspricht der ebenen Welle.Diffuse Strahlen : die einzelnen Strahlen verlaufen wahllos zueinander, Gegensatz zu homozentrischen Strahlen. Sie entstehen z.B. bei der Reflexion paralleler Strahlung an einer rauen Oberfläche.
n
m
=
c
c
m
{\displaystyle n_{\mathrm {m} }={\frac {c}{c_{\mathrm {m} }}}}
c
{\displaystyle c}
c
m
{\displaystyle c_{\mathrm {m} }}
≈
3
⋅
10
8
m
s
{\displaystyle \approx 3\cdot 10^{8}{\frac {\mathrm {m} }{\mathrm {s} }}}
n
m
{\displaystyle n_{\mathrm {m} }}
≈
1
{\displaystyle \approx 1}
c
1
c
2
=
n
2
n
1
{\displaystyle {\frac {c_{1}}{c_{2}}}={\frac {n_{2}}{n_{1}}}}
α
=
α
′
{\displaystyle \alpha =\alpha '}
α
{\displaystyle \alpha }
α
′
{\displaystyle \alpha '}
e
r
−
e
i
=
2
e
A
cos
α
{\displaystyle {{\mathbf {e} }_{r}}-{{\mathbf {e} }_{i}}=2{{\mathbf {e} }_{A}}\cos \alpha }
e
i
{\displaystyle {{\mathbf {e} }_{i}}}
e
r
{\displaystyle {{\mathbf {e} }_{r}}}
e
A
{\displaystyle {{\mathbf {e} }_{A}}}
E
(
r
,
z
)
=
E
0
w
0
w
(
z
)
e
−
r
2
w
2
(
z
)
e
−
i
k
r
2
2
R
z
+
i
ζ
(
z
)
{\displaystyle E(r,z)=E_{0}{\frac {w_{0}}{w(z)}}e^{\frac {-r^{2}}{w^{2}(z)}}e^{-ik{\frac {r^{2}}{2Rz+i\zeta (z)}}}}
I
(
r
,
z
)
=
I
0
(
w
0
w
(
z
)
)
2
e
−
2
r
2
w
2
(
z
)
{\displaystyle I(r,z)=I_{0}\left({\frac {w_{0}}{w(z)}}\right)^{2}e^{\frac {-2r^{2}}{w^{2}(z)}}}
w
(
z
)
=
w
0
1
+
(
z
z
0
)
2
{\displaystyle w(z)=w_{0}\,{\sqrt {1+{\left({\frac {z}{z_{0}}}\right)}^{2}}}}
z
0
=
π
⋅
w
0
2
λ
{\displaystyle z_{0}={\frac {\pi \cdot w_{0}^{2}}{\lambda }}}
Parallelstrahlen (Strahlen parallel zur optischen Achse) werden zu Brennpunktstrahlen (führen durch den Brennpunkt).
Mittelpunktstrahlen werden nicht abgelenkt.
Strahlengänge sind umkehrbar (also werden auch Brennpunktstrahlen zu Parallelstrahlen). Der Abbildungsmaßstab A ist das Verhältnis von Bildgröße B zu Gegenstandsgröße G .
A
=
B
G
{\displaystyle A={\frac {B}{G}}}
Für die Brechung eines Lichtstrahls beim Übergang Vakuum
→
{\displaystyle \rightarrow }
Medium
sin
(
Θ
1
)
sin
(
Θ
2
)
=
c
0
c
=
n
{\displaystyle {\frac {\sin(\Theta _{1})}{\sin(\Theta _{2})}}={\frac {c_{0}}{c}}=n}
Für den Übergang Medium 1
→
{\displaystyle \rightarrow }
Medium 2 gilt:
sin
(
Θ
1
)
sin
(
Θ
2
)
=
c
1
c
2
=
n
2
n
1
o
d
e
r
n
1
sin
(
Θ
1
)
=
n
2
sin
(
Θ
2
)
{\displaystyle {\frac {\sin(\Theta _{1})}{\sin(\Theta _{2})}}={\frac {c_{1}}{c_{2}}}={\frac {n_{2}}{n_{1}}}\qquad {\rm {oder}}\qquad n_{1}\sin(\Theta _{1})=n_{2}\sin(\Theta _{2})}
wobei
Reflektionsgrad senkrecht zur Einfallsebene polarisierter Wellen
Bearbeiten
R
⊥
=
(
sin
(
Θ
1
−
Θ
2
)
sin
(
Θ
1
+
Θ
2
)
)
2
{\displaystyle R_{\perp }=\left({\frac {\sin(\Theta _{1}-\Theta _{2})}{\sin(\Theta _{1}+\Theta _{2})}}\right)^{2}}
wobei
R
⊥
{\displaystyle R_{\perp }}
Θ
1
{\displaystyle \Theta _{1}}
Θ
2
{\displaystyle \Theta _{2}}
Reflektionsgrad parallel zur Einfallsebene polarisierter Wellen
Bearbeiten
R
|
|
=
(
tan
(
Θ
1
−
Θ
2
)
tan
(
Θ
1
+
Θ
2
)
)
2
{\displaystyle R_{||}=\left({\frac {\tan(\Theta _{1}-\Theta _{2})}{\tan(\Theta _{1}+\Theta _{2})}}\right)^{2}}
wobei
R
|
|
{\displaystyle R_{||}\ }
Θ
1
{\displaystyle \Theta _{1}}
Θ
2
{\displaystyle \Theta _{2}}
Bearbeiten
R
=
(
n
1
−
n
2
n
1
+
n
2
)
2
{\displaystyle R=\left({\frac {n_{1}-n_{2}}{n_{1}+n_{2}}}\right)^{2}}
R
{\displaystyle R}
n
1
{\displaystyle n_{1}}
Brechzahl in Medium 1
n
2
{\displaystyle n_{2}}
Brechzahl in Medium 2
θ
c
=
arcsin
(
n
2
n
1
)
mit
n
1
>
n
2
{\displaystyle \theta _{\mathrm {c} }=\arcsin \left({\frac {n_{2}}{n_{1}}}\right)\quad {\text{mit}}\quad n_{1}>n_{2}}
wobei
θ
c
{\displaystyle \theta _{\mathrm {c} }}
θ
B
=
arctan
(
n
2
n
1
)
{\displaystyle \theta _{\mathrm {B} }=\arctan \left({\frac {n_{2}}{n_{1}}}\right)}
wobei
θ
B
{\displaystyle \theta _{\mathrm {B} }}
D
=
1
f
{\displaystyle D={\frac {1}{f}}}
wobei:
f
{\displaystyle f}
Erzeugen eines reellen Bildes mit einer Sammellinse Brennweite
1
f
=
(
n
n
0
−
1
)
(
1
r
1
−
1
r
2
)
{\displaystyle {\frac {1}{f}}=\left({\frac {n}{n_{\mathrm {0} }}}-1\right)\left({\frac {1}{r_{\mathrm {1} }}}-{\frac {1}{r_{\mathrm {2} }}}\right)}
wobei
f
{\displaystyle f}
Brennweite
n
{\displaystyle n}
n
0
{\displaystyle n_{\mathrm {0} }}
≈
{\displaystyle \approx }
r
1
{\displaystyle r_{1}}
(positiv bei konvexer Linsenfläche)
r
2
{\displaystyle r_{2}}
(positiv bei konvexer Linsenfläche) Linsengleichung
1
f
=
1
g
+
1
b
{\displaystyle {\frac {1}{f}}={\frac {1}{g}}+{\frac {1}{b}}}
wobei
f
{\displaystyle f}
Brennweite
g
{\displaystyle g}
b
{\displaystyle b}
Abbildungsmaßstab
A
=
B
G
=
b
g
{\displaystyle A={\frac {B}{G}}={\frac {b}{g}}}
A
=
b
−
f
f
=
f
g
−
f
{\displaystyle A={\frac {b-f}{f}}={\frac {f}{g-f}}}
1
f
=
(
n
−
n
0
n
0
)
(
1
R
1
−
1
R
2
+
(
n
−
n
0
)
d
n
R
1
R
2
)
{\displaystyle {\frac {1}{f}}=\left({\frac {n-n_{0}}{n_{0}}}\right)\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-n_{0})d}{nR_{1}R_{2}}}\right)}
R
1
,
R
2
{\displaystyle R_{1},R_{2}}
d
{\displaystyle d}
optischen Achse ),
n
0
{\displaystyle n_{0}}
n
{\displaystyle n}
f
{\displaystyle f}
S
=
D
(
b
+
g
)
g
{\displaystyle S={\frac {D(b+g)}{g}}}
wobei
D
{\displaystyle D}
S
{\displaystyle S}
b
{\displaystyle b}
g
{\displaystyle g}
V
=
tan
ϵ
tan
ϵ
0
=
O
f
O
s
0
=
s
0
f
=
25
c
m
f
{\displaystyle V={\frac {\tan \epsilon }{\tan \epsilon _{0}}}={\frac {\frac {O}{f}}{\frac {O}{s_{0}}}}={\frac {s_{0}}{f}}={\frac {25\mathrm {cm} }{f}}}
wobei
V
{\displaystyle V}
Winkelvergrößerung
ϵ
0
{\displaystyle \epsilon _{0}}
ohne Lupe
ϵ
{\displaystyle \epsilon }
s
0
{\displaystyle s_{0}}
deutliche Sehweite
O
{\displaystyle O}
f
{\displaystyle f}
Brennweite
V
=
f
o
b
f
o
k
{\displaystyle V={\frac {f_{\mathrm {ob} }}{f_{\mathrm {ok} }}}}
V
=
f
o
b
f
o
k
{\displaystyle V={\frac {f_{\mathrm {ob} }}{f_{\mathrm {ok} }}}}
V
=
(
d
−
f
o
b
)
s
0
f
o
b
f
o
k
{\displaystyle V={\frac {(d-f_{\mathrm {ob} })s_{0}}{f_{\mathrm {ob} }f_{\mathrm {ok} }}}}
wobei
Schallschnelle
ist die Geschwindigkeit schwingender Teilchen um deren Ruhelage.
Sie ergibt sich aus Frequenz f und Auslenkung y
v
=
2
π
f
⋅
y
{\displaystyle v=2\,\pi \,f\cdot y}
Schalldruck
ist der maximale Differenzdruck einer Schallwelle (Unter- bzw. Überdruck).
Er ergibt sich aus Schallschnelle, statischer Luftdichte
ρ
{\displaystyle \rho \ }
Schallgeschwindigkeit c
p
=
ρ
c
⋅
v
{\displaystyle p=\rho \,c\cdot v}
Schallintensität I
beschreibt die Schallleistung
P
{\displaystyle P}
A
{\displaystyle A}
I
=
d
P
d
A
{\displaystyle I={\frac {dP}{dA}}}
Pegelmaße
Alle Schallfeldgrößen lassen sich in Pegelmaße [dB] überführen.
Für die energetische Größe Schallintensitätspegel ergibt sich
L
(
I
)
=
10
lg
(
J
J
0
)
{\displaystyle L(I)=10\lg \left({\frac {J}{J_{0}}}\right)}
Für alle linearen Schalldruckgrößen (
p
,
ρ
,
v
{\displaystyle p,\,\rho ,\,v}
L
=
20
lg
(
p
p
0
)
{\displaystyle L=20\lg \left({\frac {p}{p_{0}}}\right)}
t
=
e
+
d
{\displaystyle t=e+d}
]
Diese Formelsammlung kommt aus den Gebieten Akustik, Psychoakustik, Elektro-Akustik, Elektrotechnik und vielen weiteren Gebiete mehr.
c
S
=
f
λ
{\displaystyle c_{\mathrm {S} }=f\,\lambda }
c
S
:
{\displaystyle c_{\mathrm {S} }:}
Schallgeschwindigkeit in m/s
f
{\displaystyle f}
Frequenz in Hz
λ
{\displaystyle \lambda }
Wellenlänge in m
c
S
=
K
ρ
{\displaystyle c_{\mathrm {S} }={\sqrt {\frac {K}{\rho }}}}
c
S
:
{\displaystyle c_{\mathrm {S} }:}
K
{\displaystyle K}
Kompressionsmodul in Pascal Pa = N/m²
ρ
{\displaystyle \rho }
Dichte , in kg/m³
c
S
=
κ
p
ρ
=
κ
R
T
M
{\displaystyle c_{\mathrm {S} }={\sqrt {\frac {\kappa \,p}{\rho }}}={\sqrt {\frac {\kappa \,R\,T}{M}}}}
p
{\displaystyle p}
Schalldruck in Pascal ) = N/m²κ = cp /cV = Adiabatenexponent
R
{\displaystyle R}
universelle Gaskonstante = 8,3145 J/molK
Die Schallgeschwindigkeit in Luft ist nicht vom Luftdruck abhängig, weil
p
ρ
{\displaystyle {\frac {p}{\rho }}}
langer Stab longitudinal :
c
l
=
E
ρ
{\displaystyle c_{\rm {l}}={\sqrt {\frac {E}{\rho }}}}
langer Stab transversal :
c
t
=
G
ρ
=
E
2
(
1
+
μ
)
ρ
{\displaystyle c_{\rm {t}}={\sqrt {\frac {G}{\rho }}}={\sqrt {\frac {E}{2(1+\mu )\rho }}}}
E
{\displaystyle E}
Elastizitätsmodul in N/m²
G
{\displaystyle G}
Schubmodul in N/m²
μ
{\displaystyle \mu }
Poissonzahl
Verschiebungsamplitude
x
0
=
v
0
ω
{\displaystyle x_{0}={\frac {v_{0}}{\omega }}}
Geschwindigkeitsamplitude (Schallschnelle )
v
0
=
ω
x
0
{\displaystyle v_{0}=\omega \,x_{0}}
Beschleunigungsamplitude
a
0
=
ω
2
x
0
{\displaystyle a_{0}=\omega ^{2}\,x_{0}}
Druckamplitude
Δ
p
0
=
Z
v
0
{\displaystyle \Delta p_{0}=Z\,v_{0}}
p
⋅
V
=
n
⋅
R
⋅
T
{\displaystyle p\cdot V=n\cdot R\cdot T}
Symbol, Größe
Einheit bzw. Wert
p : DruckPa (-->Pascal)
V : Volumenm3
n : Stoffmengemol
R : Allgemeine Gaskonstante 8,314472 J/(mol·K)
T : Absolute TemperaturK
p
T
=
const.
⇔
p
1
T
1
=
p
2
T
2
{\displaystyle {\frac {p}{T}}={\text{const.}}\qquad \Leftrightarrow \qquad {\frac {p_{1}}{T_{1}}}={\frac {p_{2}}{T_{2}}}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
T
1
{\displaystyle T_{1}}
T
2
{\displaystyle T_{2}}
T
2
=
p
2
⋅
T
1
p
1
{\displaystyle T_{2}={\frac {p_{2}\cdot T_{1}}{p_{1}}}}
T
1
{\displaystyle T_{1}}
T
2
{\displaystyle T_{2}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
p
2
=
p
1
⋅
T
2
T
1
{\displaystyle p_{2}={\frac {p_{1}\cdot T_{2}}{T_{1}}}}
Symbol, Größe
Einheit bzw. Wert
p
1
{\displaystyle p_{1}}
Pa
p
2
{\displaystyle p_{2}}
Pa
T
1
{\displaystyle T_{1}}
K1
T
2
{\displaystyle T_{2}}
K1
p
⋅
V
=
const.
⇔
p
1
⋅
V
1
=
p
2
⋅
V
2
{\displaystyle p\cdot V={\text{const.}}\qquad \Leftrightarrow \qquad p_{1}\cdot V_{1}=p_{2}\cdot V_{2}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
V
1
{\displaystyle V_{1}}
V
2
{\displaystyle V_{2}}
V
2
=
p
1
⋅
V
1
p
2
{\displaystyle V_{2}={\frac {p_{1}\cdot V_{1}}{p_{2}}}}
V
1
{\displaystyle V_{1}}
V
2
{\displaystyle V_{2}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
p
2
=
p
1
⋅
V
1
V
2
{\displaystyle p_{2}={\frac {p_{1}\cdot V_{1}}{V_{2}}}}
Symbol, Größe
Einheit bzw. Wert
p
1
{\displaystyle p_{1}}
Pa
p
2
{\displaystyle p_{2}}
Pa
V
1
{\displaystyle V_{1}}
m³
V
2
{\displaystyle V_{2}}
m³
V
T
=
const.
⇔
V
1
T
1
=
V
2
T
2
{\displaystyle {V \over T}={\text{const.}}\qquad \Leftrightarrow \qquad {\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}}
T
1
{\displaystyle T_{1}}
T
2
{\displaystyle T_{2}}
V
1
{\displaystyle V_{1}}
V
2
{\displaystyle V_{2}}
V
2
=
V
1
⋅
T
2
T
1
{\displaystyle V_{2}={\frac {V_{1}\cdot T_{2}}{T_{1}}}}
V
1
{\displaystyle V_{1}}
V
2
{\displaystyle V_{2}}
T
1
{\displaystyle T_{1}}
T
2
{\displaystyle T_{2}}
T
2
=
T
1
⋅
V
2
V
1
{\displaystyle T_{2}={\frac {T_{1}\cdot V_{2}}{V_{1}}}}
Symbol, Größe
Einheit bzw. Wert
V
1
{\displaystyle V_{1}}
m³
V
2
{\displaystyle V_{2}}
m³
T
1
{\displaystyle T_{1}}
K
T
2
{\displaystyle T_{2}}
K
Bearbeiten
Bei gegebenen Abmessungen
A
,
l
{\displaystyle A,l\ }
ρ
t
h
{\displaystyle \rho _{\mathrm {th} }\ }
R
t
h
{\displaystyle R_{\mathrm {th} }\ }
R
t
h
=
ρ
t
h
⋅
l
A
{\displaystyle R_{\mathrm {th} }={\frac {\rho _{\mathrm {th} }\cdot l}{A}}}
Aus der Temperaturdifferenz
Δ
T
{\displaystyle \Delta T\ }
Q
˙
{\displaystyle {\dot {Q}}}
ρ
t
h
=
Δ
T
⋅
A
Q
˙
⋅
l
{\displaystyle \rho _{\mathrm {th} }={\frac {\Delta T\cdot A}{{\dot {Q}}\cdot l}}}
mit
ρ
t
h
{\displaystyle \rho _{\mathrm {th} }\ }
Δ
T
{\displaystyle \Delta T\ }
A
{\displaystyle A\ }
l
{\displaystyle l\ }
Q
˙
{\displaystyle {\dot {Q}}}
Q
=
c
⋅
m
⋅
Δ
T
{\displaystyle Q=c\cdot m\cdot \Delta T}
mit
Q
{\displaystyle Q\ }
c
{\displaystyle c\ }
m
{\displaystyle m\ }
Δ
T
{\displaystyle \Delta T\ }
Q
˙
=
c
⋅
m
˙
⋅
Δ
T
{\displaystyle {\dot {Q}}=c\cdot {\dot {m}}\cdot \Delta T}
mit
Q
˙
{\displaystyle {\dot {Q}}}
m
˙
{\displaystyle {\dot {m}}}
Q
˙
=
λ
s
⋅
A
⋅
Δ
T
{\displaystyle {\dot {Q}}={\frac {\lambda }{s}}\cdot A\cdot \Delta T}
mit
Q
˙
{\displaystyle {\dot {Q}}}
λ
{\displaystyle \lambda }
s
{\displaystyle s}
A
{\displaystyle A}
Δ
T
{\displaystyle \Delta T\ }
Bearbeiten
Q
˙
=
U
⋅
A
⋅
Δ
T
{\displaystyle {\dot {Q}}=U\cdot A\cdot \Delta T}
mit
Q
˙
{\displaystyle {\dot {Q}}}
= Wärmestrom [W]
U
{\displaystyle U}
= Wärmedurchgangskoeffizient [W/(m²K)] - {ALTE BEZEICHNUNG "k"}
A
{\displaystyle A}
= Fläche [m²]
Δ
T
{\displaystyle \Delta T}
= Temperaturdifferenz (in Kelvin)
U gilt:
U
=
1
R
T
=
1
R
s
e
+
d
λ
+
R
s
i
{\displaystyle U={\frac {1}{R_{\mathrm {T} }}}={\frac {1}{R_{\mathrm {se} }+{\frac {d}{\lambda }}+R_{\mathrm {si} }}}}
mit
R
i
n
d
e
x
{\displaystyle {R_{\mathrm {index} }}}
d
{\displaystyle d}
λ
{\displaystyle \lambda }
Setzt sich aus den Wärmedurchlasswiderständen der einzelnen Wandschichten zusammen.
d
λ
=
d
1
λ
1
+
d
2
λ
2
+
…
{\displaystyle {\frac {d}{\lambda }}={\frac {d_{1}}{\lambda _{1}}}+{\frac {d_{2}}{\lambda _{2}}}+\dots }
mit
d
{\displaystyle d}
λ
{\displaystyle \lambda }
Q
p
=
ϵ
⋅
σ
⋅
A
⋅
T
4
{\displaystyle Q_{p}=\epsilon \cdot \sigma \cdot A\cdot T^{4}}
mit
Q
p
{\displaystyle Q_{p}}
ϵ
{\displaystyle \epsilon }
σ
{\displaystyle \sigma }
2 K4 ]A = Fläche [m²]T = Temperatur
Formelzeichen
Einheit
Q Ladung
C Coulomb
[
Q
]
=
[
I
]
⋅
[
t
]
{\displaystyle [Q]=[I]\cdot [t]}
C
=
A
⋅
s
{\displaystyle C=A\cdot s}
Q
=
∫
t
I
(
t
)
d
t
{\displaystyle Q=\int _{t}I(t)\mathrm {d} t\ }
Allgemein
Ladung Q im Kondensator
Q
=
C
⋅
U
{\displaystyle Q=C\cdot U}
Energie W im Kondensator
W
=
1
2
C
⋅
U
2
{\displaystyle W={\frac {1}{2}}\ C\cdot U^{2}}
Strom in den Kondensator
I
=
C
⋅
d
U
d
t
{\displaystyle I=C\cdot {\frac {dU}{dt}}\ }
Laden / Entladen in Reihenschaltung
Anfangsladestrom
I
=
U
R
{\displaystyle I={\frac {U}{R}}}
Zeitkonstante
τ
{\displaystyle \tau }
τ
=
R
⋅
C
{\displaystyle \tau =R\cdot C}
Kondensatorspannung beim Ladevorgang
u
c
=
U
⋅
(
1
−
e
−
t
τ
)
{\displaystyle u_{c}=U\cdot (1-e^{-{\frac {t}{\tau }}})}
Ladestrom
i
c
=
U
R
⋅
e
−
t
τ
{\displaystyle i_{c}={\frac {U}{R}}\cdot e^{-{\frac {t}{\tau }}}}
Kondensatorspannung beim Entladevorgang
u
c
=
U
⋅
e
−
t
τ
{\displaystyle u_{c}=U\cdot e^{-{\frac {t}{\tau }}}}
Entladestrom
i
c
=
−
U
R
⋅
e
−
t
τ
{\displaystyle i_{c}=-{\frac {U}{R}}\cdot e^{-{\frac {t}{\tau }}}}
Reihenschaltung von Kondensatoren
Parallelschaltung von Kondensatoren
U
g
=
U
1
+
U
2
+
⋯
+
U
n
{\displaystyle U_{g}=U_{1}+U_{2}+\dots +U_{n}\ }
Q
g
=
Q
1
+
Q
2
+
⋯
+
Q
n
{\displaystyle Q_{g}=Q_{1}+Q_{2}+\dots +Q_{n}\ }
1
C
g
=
1
C
1
+
1
C
2
+
⋯
+
1
C
n
{\displaystyle {\frac {1}{C_{g}}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\dots +{\frac {1}{C_{n}}}}
C
g
=
C
1
+
C
2
+
⋯
+
C
n
{\displaystyle C_{g}=C_{1}+C_{2}+\dots +C_{n}\ }
U
1
U
2
=
C
2
C
1
{\displaystyle {\frac {U_{1}}{U_{2}}}={\frac {C_{2}}{C_{1}}}}
Q
1
Q
2
=
C
1
C
2
{\displaystyle {\frac {Q_{1}}{Q_{2}}}={\frac {C_{1}}{C_{2}}}}
Für n gleiche C
C
g
=
C
n
{\displaystyle C_{g}={\frac {C}{n}}}
Für n gleiche C
C
g
=
n
⋅
C
{\displaystyle C_{g}=n\cdot C}
Formelzeichen
I
{\displaystyle I\ }
Einheit
Ampere Das Ampere ist eine SI-Basiseinheit und hat daher keine Definitionsgleichung
A
{\displaystyle \mathrm {A} \ }
Elektronen werden durch Kraftwirkung Beschleunigt
F
→
=
−
e
E
→
{\displaystyle \mathrm {\vec {F}} =-e{\vec {E}}}
Elektronen werden beschleunigt bis es z. B. ein Gitteratom stößt:
v
D
→
=
∫
0
τ
m
(
−
e
)
E
→
m
e
=
−
(
e
τ
m
m
)
E
→
=
−
μ
n
E
→
{\displaystyle {\vec {v_{D}}}=\int _{0}^{\tau _{m}}{\frac {(-e){\vec {E}}}{m_{e}}}=-\left({\frac {e\tau _{m}}{m}}\right){\vec {E}}=-\mu _{n}{\vec {E}}}
wobei
τ
m
{\displaystyle \tau _{m}}
v
D
{\displaystyle v_{D}}
Driftgeschwindigkeit : Ist die mittlere Geschwindigkeit, die von Feldstärke verursachen wird.
m
e
{\displaystyle m_{e}}
μ
n
{\displaystyle \mu _{n}}
Einheit
Ampere *Meter^-2
J
→
=
ρ
v
→
D
=
n
e
v
D
→
{\displaystyle {\vec {J}}=\rho \;{\vec {v}}_{D}=n\;e\;{\vec {v_{D}}}}
ρ
{\displaystyle \rho }
n
{\displaystyle n}
e
{\displaystyle e}
I
=
∬
A
J
→
⋅
d
A
→
{\displaystyle I=\iint \limits _{A}{\vec {J}}\cdot \mathrm {d} {\vec {A}}}
Wenn Homogen
I
=
J
⋅
A
{\displaystyle I=J\cdot A}
Es gilt nur wenn Strom konstant ist, und wenn es keine Ladung in die Hüllfläche gibt.
0
=
{\displaystyle 0=}
A
{\displaystyle A}
J
→
⋅
d
A
→
{\displaystyle {\vec {J}}\cdot \mathrm {d} {\vec {A}}}
Formelzeichen
R
=
U
I
{\displaystyle R={\frac {U}{I}}}
Einheit
Ohm
1
Ω
=
V
A
=
k
g
⋅
m
2
s
3
⋅
A
2
{\displaystyle 1\Omega ={\frac {\mathrm {V} }{\mathrm {A} }}={\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{3}\cdot \mathrm {A} ^{2}}}}
konstant ist, gilt übrigens nur bei konstanter Temperatur und metallischen Leitern !
Für den Fall, dass der Widerstand sich mit der Temperatur ändert, gilt folgende Gesetzmäßigkeit:
R
θ
=
R
20
⋅
(
1
+
α
⋅
Δ
θ
)
{\displaystyle R_{\theta }=R_{20}\cdot \left(1+\alpha \cdot \Delta \theta \right)}
Der Widerstand bei einer Temperatur ist der Widerstand bei einer bekannten Temperatur multipliziert mit einem Faktor, der von einer Materialkonstante α abhängt und der Temperaturdifferenz
Δ
θ
{\displaystyle \Delta \theta }
Bearbeiten
U
=
I
⋅
R
{\displaystyle U=I\cdot R}
I
=
U
R
{\displaystyle I={\frac {U}{R}}}
R
=
U
I
{\displaystyle R={\frac {U}{I}}}
I
=
U
⋅
G
{\displaystyle I=U\cdot G}
U
=
I
G
{\displaystyle U={\frac {I}{G}}}
G
=
I
U
{\displaystyle G={\frac {I}{U}}}
1
=
R
⋅
G
{\displaystyle 1=R\cdot G}
R
=
1
G
{\displaystyle R={\frac {1}{G}}}
G
=
1
R
{\displaystyle G={\frac {1}{R}}}
P
=
U
⋅
I
{\displaystyle P=U\cdot I}
U
=
P
I
{\displaystyle U={\frac {P}{I}}}
I
=
P
U
{\displaystyle I={\frac {P}{U}}}
P
=
U
2
R
{\displaystyle P={\frac {U^{2}}{R}}}
P
=
I
2
⋅
R
{\displaystyle P={I^{2}}\cdot {R}}
U
=
P
⋅
R
{\displaystyle U={\sqrt {P\cdot R}}}
I
=
P
R
{\displaystyle I={\sqrt {\frac {P}{R}}}}
R
=
U
2
P
{\displaystyle R={\frac {U^{2}}{P}}}
R
=
P
I
2
{\displaystyle R={\frac {P}{I^{2}}}}
W
=
P
⋅
t
{\displaystyle W=P\cdot t}
P
=
W
t
{\displaystyle P={\frac {W}{t}}}
t
=
W
P
{\displaystyle t={\frac {W}{P}}}
W
=
U
⋅
I
⋅
t
{\displaystyle W=U\cdot I\cdot t}
2. Kirchhoff'sches Gesetz, auch Maschenregel genannt.
Die Summe aller Teilspannungen ist genauso groß wie die Gesamtspannung
Formelzeiche
Beschreibung
Formelzeichen
Beschreibung
Formelzeichen
Beschreibung
R ges
Gesamtwiderstand
R 1
Teilwiderstand
R 2
Teilwiderstand
U ges
Gesamtspannung
U R 1 Spannung an R 1
U R 2 Spannung an R 2
P ges
Gesamtleistung
P R 1 Leistung an R 1
P R 2 Leistung an R 2
I
g
e
s
=
I
R
1
=
I
R
2
=
⋯
=
I
R
n
{\displaystyle I_{\mathrm {ges} }=I_{R_{1}}=I_{R_{2}}=\dots =I_{R_{n}}}
R
g
e
s
=
R
1
+
R
2
+
⋯
+
R
n
{\displaystyle R_{\mathrm {ges} }=R_{1}+R_{2}+\dots +R_{n}}
U
g
e
s
=
U
R
1
+
U
R
2
+
⋯
+
U
R
n
{\displaystyle U_{\mathrm {ges} }=U_{R_{1}}+U_{R_{2}}+\dots +U_{R_{n}}}
P
g
e
s
=
P
R
1
+
P
R
2
+
⋯
+
P
R
n
{\displaystyle P_{\mathrm {ges} }=P_{R_{1}}+P_{R_{2}}+\dots +P_{R_{n}}}
P
R
1
=
U
R
1
⋅
I
{\displaystyle P_{R_{1}}=U_{R_{1}}\cdot I}
U
R
1
=
U
g
e
s
⋅
R
1
R
g
e
s
{\displaystyle U_{R_{1}}=U_{\mathrm {ges} }\cdot {\frac {R_{1}}{R_{\mathrm {ges} }}}}
1. Kirchhoff'sches Gesetz, auch Knotenregel genannt.
Die Summe aller Teilströme ist genauso groß wie der Gesamtstrom
Formelzeichen
Beschreibung
Formelzeichen
Beschreibung
Formelzeichen
Beschreibung
R ges
Gesamtwiderstand
R 1
Teilwiderstand
R 2
Teilwiderstand
G ges
Gesamtleitwert
G 1
Leitwert von Teilwiderstand R 1
G 2
Leitwert von Teilwiderstand R 2
I ges
Gesamtstromstärke
I R 1 Stromstärke an R 1
I R 2 Stromstärke an R 2
P ges
Gesamtleistung
P R 1 Leistung an R 1
P R2
Leistung an R 2
U
g
e
s
=
U
R
1
=
U
R
2
=
⋯
=
U
R
n
{\displaystyle U_{\mathrm {ges} }=U_{R_{1}}=U_{R_{2}}=\dots =U_{R_{n}}}
R
g
e
s
=
1
1
R
1
+
1
R
2
+
⋯
+
1
R
n
{\displaystyle R_{\mathrm {ges} }={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\dots +{\frac {1}{R_{n}}}}}}
G
g
e
s
=
G
1
+
G
2
+
⋯
+
G
n
{\displaystyle G_{\mathrm {ges} }=G_{1}+G_{2}+\dots +G_{n}}
R
g
e
s
=
1
G
1
+
G
2
+
⋯
+
G
n
{\displaystyle R_{\mathrm {ges} }={\frac {1}{G_{1}+G_{2}+\dots +G_{n}}}}
I
g
e
s
=
I
R
1
+
I
R
2
+
⋯
+
I
R
n
{\displaystyle I_{\mathrm {ges} }=I_{R_{1}}+I_{R_{2}}+\dots +I_{R_{n}}}
P
g
e
s
=
P
R
1
+
P
R
2
+
⋯
+
P
R
n
{\displaystyle P_{\mathrm {ges} }=P_{R_{1}}+P_{R_{2}}+\dots +P_{R_{n}}}
P
R
1
=
U
⋅
I
R
1
{\displaystyle P_{R_{1}}=U\cdot I_{R_{1}}}
[
ρ
]
=
Ω
⋅
m
m
2
m
{\displaystyle [\rho ]={\frac {\Omega \cdot \mathrm {mm} ^{2}}{\mathrm {m} }}}
Tabelle für den spezifischen Widerstand
R
=
ρ
⋅
l
A
{\displaystyle R={\frac {\rho \cdot l}{A}}}
[
γ
]
=
m
Ω
⋅
m
m
2
{\displaystyle [\gamma ]={\frac {\mathrm {m} }{\Omega \cdot \mathrm {mm} ^{2}}}}
R
=
l
γ
⋅
A
{\displaystyle R={\frac {l}{\gamma \cdot A}}}
elektrische Spannung U
U
=
W
Q
{\displaystyle U={\frac {W}{Q}}}
t
{\displaystyle t}
Q
{\displaystyle Q}
W
{\displaystyle W}
ϑ
{\displaystyle \vartheta }
ρ
=
{\displaystyle \rho =}
elektrische Strom-
I
=
d
Q
d
t
{\displaystyle I={\frac {dQ}{dt}}}
I = konstant) gilt:
I
=
Q
t
{\displaystyle I={\frac {Q}{t}}}
elektrischer Wider-
R
=
U
I
{\displaystyle R={\frac {U}{I}}}
elektrischer Leitwert G
G
=
1
R
{\displaystyle G={\frac {1}{R}}}
elektrische Leistung P
P
=
U
⋅
I
{\displaystyle P=U\cdot I}
elektrische Arbeit W
W
=
P
⋅
t
{\displaystyle W=P\cdot t}
ohmsches Gesetz
Unter der Bedingung
ϑ
=
k
o
n
s
t
a
n
t
{\displaystyle \vartheta =\mathrm {konstant} }
U
∼
I
,
U
I
=
k
o
n
s
t
a
n
t
{\displaystyle U\sim I,{\frac {U}{I}}=\mathrm {konstant} }
Widerstandsgesetz
R
=
ρ
⋅
l
A
{\displaystyle R={\frac {\rho \cdot l}{A}}}
elektrische Leitfähigkeit
γ
=
1
ρ
{\displaystyle \gamma ={\frac {1}{\rho }}}
Unverzweigter und verzweigter Gleichstromkreis
Bearbeiten
Reihenschaltung von Widerständen
Parallelschaltung von Widerständen
I
=
I
1
=
I
2
=
⋯
=
I
n
{\displaystyle I=I_{1}=I_{2}=\dots =I_{n}\ }
I
=
I
1
+
I
2
+
⋯
+
I
n
{\displaystyle I=I_{1}+I_{2}+\dots +I_{n}\ }
U
=
U
1
+
U
2
+
⋯
+
U
n
{\displaystyle U=U_{1}+U_{2}+\dots +U_{n}\ }
U
=
U
1
=
U
2
=
⋯
=
U
n
{\displaystyle U=U_{1}=U_{2}=\dots =U_{n}\ }
R
=
R
1
+
R
2
+
⋯
+
R
n
{\displaystyle R=R_{1}+R_{2}+\dots +R_{n}\ }
1
R
=
1
R
1
+
1
R
2
+
⋯
+
1
R
n
{\displaystyle {\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\dots +{\frac {1}{R_{n}}}\ }
Spannungsteilerregel:
U
1
U
2
=
R
1
R
2
U
1
U
=
R
1
R
{\displaystyle {\frac {U_{1}}{U_{2}}}={\frac {R_{1}}{R_{2}}}\qquad {\frac {U_{1}}{U}}={\frac {R_{1}}{R}}}
Stromteilerregel:
I
2
I
1
=
R
1
R
2
I
1
I
=
R
R
1
{\displaystyle {\frac {I_{2}}{I_{1}}}={\frac {R_{1}}{R_{2}}}\qquad {\frac {I_{1}}{I}}={\frac {R}{R_{1}}}}
Reihenschaltung von Spannungsquellen
Parallelschaltung von Spannungsquellen
U
=
U
1
+
U
2
+
⋯
+
U
n
{\displaystyle U=U_{1}+U_{2}+\dots +U_{n}}
Unter der Bedingung gleicher Spannungsquellen gilt:
U
=
U
1
=
U
2
=
.
.
.
=
U
n
{\displaystyle U=U_{1}=U_{2}=...=U_{n}}
Formelzeichen
Einheit
B
→
{\displaystyle {\vec {B}}}
Magnetische Flussdichte
T Tesla
[
B
→
]
=
[
U
]
⋅
[
t
]
[
s
]
2
{\displaystyle [{\vec {B}}]={\frac {[U]\cdot [t]}{[s]^{2}}}}
T
=
V
⋅
s
m
2
{\displaystyle T={\frac {V\cdot s}{m^{2}}}}
B
→
=
μ
0
(
H
→
+
M
→
)
=
μ
H
→
{\displaystyle \mathbf {\vec {B}} =\mu _{0}(\mathbf {{\vec {H}}+{\vec {M}}} )=\mu \mathbf {\vec {H}} }
Magnetische Wirkung eine ladung in andere Ladung:
F
→
m
a
g
,
Q
2
=
(
Q
2
v
→
2
)
×
μ
(
Q
1
v
1
→
)
×
r
→
r
3
=
(
Q
2
v
→
2
)
×
B
→
{\displaystyle {\vec {F}}_{mag,Q_{2}}=(Q_{2}{\vec {v}}_{2})\times \mu {\frac {(Q_{1}{\vec {v_{1}}})\times {\vec {r}}}{r^{3}}}=(Q_{2}{\vec {v}}_{2})\times {\vec {\mathbf {B} }}}
wobei
μ
=
μ
0
μ
r
{\displaystyle \mu =\mu _{0}\mu _{r}}
μ
{\displaystyle \mu }
Permeabilität
μ
0
{\displaystyle \mu _{0}\,}
magnetische Feldkonstante
≈
4
π
⋅
10
−
7
N
A
2
{\displaystyle \approx 4\pi \cdot 10^{-7}{\frac {\mathrm {N} }{\mathrm {A} ^{2}}}}
μ
r
{\displaystyle \mu _{\rm {r}}\,}
π
{\displaystyle \pi \,}
Kreiszahl
=
3,141
59265
…
{\displaystyle =\,3{,}14159265\dots }
Q
1
,
Q
2
{\displaystyle Q_{1}\,,\,Q_{2}}
v
→
1
,
v
→
2
{\displaystyle {\vec {v}}_{1}\,,\,{\vec {v}}_{2}}
r
→
{\displaystyle {\vec {r}}\,}
Abstandsvektor der Ladungen
r
=
|
r
→
|
{\displaystyle r\,=\,|{\vec {r}}|\,}
und
B
→
=
μ
0
H
→
{\displaystyle {\overrightarrow {\mathbf {B} }}=\mu _{0}{\overrightarrow {\mathbf {H} }}}
μ
0
ε
0
=
1
c
2
{\displaystyle \mu _{0}\varepsilon _{0}={\frac {1}{c^{2}}}}
Formelzeichen
Einheit
H
→
{\displaystyle {\vec {H}}}
Magnetische Feldstärke
A/m
[
H
]
{\displaystyle [H]}
A
m
{\displaystyle {\frac {A}{m}}}
B
→
=
μ
0
(
H
→
+
M
→
)
=
μ
H
→
{\displaystyle \mathbf {\vec {B}} =\mu _{0}(\mathbf {{\vec {H}}+{\vec {M}}} )=\mu \mathbf {\vec {H}} }
F
L
=
q
(
v
×
B
)
=
I
ℓ
×
B
{\displaystyle {\boldsymbol {F}}_{L}=q\left({\boldsymbol {v}}\times {\boldsymbol {B}}\right)=I\,\mathbf {\ell } \times \mathbf {B} }
Für einer unendliche lange Leiter gilt:
B
→
=
μ
I
2
π
ρ
e
ρ
→
{\displaystyle {\vec {B}}={\frac {\mu \;I}{2\pi \rho }}{\vec {e_{\rho }}}}
∮
H
→
⋅
d
s
→
=
Θ
{\displaystyle \oint {\vec {H}}\cdot d{\vec {s}}=\Theta }
Formelzeichen
Einheit
Φ
{\displaystyle \Phi }
Magnetischer Fluss
Weber
[
Φ
]
=
[
U
]
⋅
[
t
]
{\displaystyle [\Phi ]=[U]\cdot [t]}
W
b
=
V
⋅
s
{\displaystyle Wb=V\cdot s}
Φ
=
∮
∂
V
B
→
⋅
d
A
→
=
∫
V
∇
⋅
B
→
d
V
{\displaystyle \Phi =\oint \limits _{\partial V}{\vec {B}}\cdot \mathrm {d} {\vec {A}}=\int \limits _{V}\nabla \cdot {\vec {B}}\;\mathrm {d} V}
Formelzeichen
Einheit
L
{\displaystyle L}
Induktivität
Henry
[
L
]
=
[
Φ
]
[
I
]
{\displaystyle [L]={\frac {[\Phi ]}{[I]}}}
H
=
W
b
A
{\displaystyle H={\frac {Wb}{A}}}
Induktivität ist verketterter magnetische Fluss durch Ström
Ablenkung im Kondensator
y
1
=
1
4
⋅
U
y
U
A
⋅
l
2
d
{\displaystyle y_{1}={\frac {1}{4}}\cdot {\frac {U_{y}}{U_{A}}}\cdot {\frac {l^{2}}{d}}}
U
y
{\displaystyle U_{y}}
U
A
{\displaystyle U_{A}}
l
{\displaystyle l}
d
{\displaystyle d}
s
{\displaystyle s}
Ablenkung außerhalb des Kondensator
y
2
=
1
2
⋅
U
y
U
A
⋅
l
⋅
s
d
{\displaystyle y_{2}={\frac {1}{2}}\cdot {\frac {U_{y}}{U_{A}}}\cdot {\frac {l\cdot s}{d}}}
Gesamte Ablenkung
y
=
1
2
⋅
U
y
U
A
⋅
l
d
(
l
2
+
s
)
{\displaystyle y={\frac {1}{2}}\cdot {\frac {U_{y}}{U_{A}}}\cdot {\frac {l}{d}}\left({\frac {l}{2}}+s\right)}
U
1
U
2
=
N
1
N
2
{\displaystyle {\frac {U_{1}}{U_{2}}}={\frac {N_{1}}{N_{2}}}}
I
1
I
2
=
N
2
N
1
{\displaystyle {\frac {I_{1}}{I_{2}}}={\frac {N_{2}}{N_{1}}}}
I
1
I
2
=
U
2
U
1
{\displaystyle {\frac {I_{1}}{I_{2}}}={\frac {U_{2}}{U_{1}}}}
U
1
{\displaystyle U_{1}}
U
2
{\displaystyle U_{2}}
N
1
{\displaystyle N_{1}}
N
2
{\displaystyle N_{2}}
I
1
{\displaystyle I_{1}}
I
2
{\displaystyle I_{2}}
Bearbeiten
Q bzw. q =
Ψ
{\displaystyle \Psi }
Q ] = C = As (Coulomb = Ampere Sekunde)
e
=
1,602
17662
⋅
10
−
19
A
s
{\displaystyle e=\,1{,}60217662\cdot 10^{-19}\mathrm {As} }
Die Ladung ist vielfaches der elektrische Elementarladung
e
{\displaystyle e}
Q
=
e
N
mit
N
∈
Z
{\displaystyle Q=eN\quad {\text{mit}}\quad N\in \mathbb {Z} }
λ
(
r
→
)
=
d
Q
d
l
⇔
Q
=
∫
l
λ
(
r
→
)
d
l
.
{\displaystyle \lambda ({\vec {r}})={\frac {\mathrm {d} Q}{\mathrm {d} l}}\quad \Leftrightarrow \quad Q=\int _{l}\lambda ({\vec {r}})\,\mathrm {d} l.}
σ
(
r
→
)
=
d
Q
d
A
⇔
Q
=
∫
A
σ
(
r
→
)
d
A
{\displaystyle \sigma ({\vec {r}})={\frac {\mathrm {d} Q}{\mathrm {d} A}}\quad \Leftrightarrow \quad Q=\int _{A}\sigma ({\vec {r}})\,\mathrm {d} A}
ρ
(
r
→
)
=
d
Q
d
V
⇔
Q
=
∫
V
ρ
(
r
→
)
d
V
{\displaystyle \rho ({\vec {r}})={\frac {\mathrm {d} Q}{\mathrm {d} V}}\quad \Leftrightarrow \quad Q=\int _{V}\rho ({\vec {r}})\,\mathrm {d} V}
Q
t
o
t
=
∑
i
Q
i
=
∫
V
q
i
⋅
d
V
{\displaystyle Q_{\mathrm {tot} }=\sum _{i}Q_{i}=\int \limits _{V}{q_{i}\,\cdot \,\mathrm {d} V}}
Q
t
o
t
{\displaystyle Q_{\mathrm {tot} }\,}
Q
i
/
q
i
{\displaystyle Q_{i}/q_{i}}
V
,
d
V
{\displaystyle V,\mathrm {d} V}
w:infinitesimales Volumenelementskalar:
F
=
1
4
π
ε
⋅
Q
1
Q
2
r
2
mit
ε
=
ε
0
ε
r
{\displaystyle F={\frac {1}{4\pi \varepsilon }}\,\cdot \,{\frac {Q_{1}Q_{2}}{r^{2}}}\qquad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\rm {r}}}
vektoriell:
F
→
=
1
4
π
ε
⋅
Q
1
Q
2
r
2
⋅
r
→
r
mit
ε
=
ε
0
ε
r
{\displaystyle {\vec {F}}\,=\,{\frac {1}{4\pi \varepsilon }}\,\cdot \,{\frac {Q_{1}Q_{2}}{r^{2}}}\,\cdot \,{\frac {\vec {r}}{r}}\qquad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\rm {r}}}
ε
{\displaystyle \varepsilon \,}
w:Permittivität (Dielektrizitätszahl)
ε
0
{\displaystyle \varepsilon _{0}\,}
w:elektrische Feldkonstante
=
8,854
18782
⋯
⋅
10
−
12
A
s
V
m
{\displaystyle =\,8{,}85418782\dots \cdot 10^{-12}\,{\frac {\rm {As}}{\rm {Vm}}}}
ε
r
{\displaystyle \varepsilon _{\mathrm {r} }\,}
π
{\displaystyle \pi \,}
w:Kreiszahl
=
3,141
59265
…
{\displaystyle =\,3{,}14159265\dots }
Q
1
,
Q
2
{\displaystyle Q_{1},Q_{2}}
r
→
{\displaystyle {\vec {r}}\,}
w:vektor der Ladungen
r
=
|
r
→
|
{\displaystyle r=|{\vec {r}}|\,}
skalar:
Ψ
=
Q
=
∑
ε
⋅
E
N
⋅
Δ
A
mit
ε
=
ε
0
ε
r
{\displaystyle \Psi =Q=\sum {\varepsilon \,\cdot E_{N}\,\cdot \,\Delta A}\qquad {\textrm {mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{r}}
wenn homogen:
Ψ
=
Q
=
{\displaystyle \Psi =Q=}
A
{\displaystyle A}
D
⋅
d
A
{\displaystyle D\,\cdot \,\mathrm {d} A}
vektoriell:
Ψ
=
Q
=
{\displaystyle \Psi =Q=}
A
{\displaystyle A}
ε
⋅
E
→
⋅
d
A
→
m
i
t
ε
=
ε
0
ε
r
{\displaystyle \varepsilon \,\cdot {\vec {E}}\,\cdot \,{\vec {\mathrm {d} A}}\quad \mathrm {mit} \quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }}
Ψ
=
Q
=
{\displaystyle \Psi =Q=}
A
{\displaystyle A}
D
→
⋅
d
A
→
{\displaystyle {\vec {D}}\,\cdot \,{\vec {\mathrm {d} A}}}
Ψ
=
∑
A
Q
e
{\displaystyle \Psi \,=\,\sum _{A}{Q_{e}}}
Q
e
{\displaystyle Q_{e}}
ε
{\displaystyle \varepsilon \,}
ε
0
{\displaystyle \varepsilon _{0}\,}
=
8,854
18782
⋯
⋅
10
−
12
A
s
V
m
{\displaystyle =\,8{,}85418782\dots \cdot 10^{-12}\,{\frac {\mathrm {As} }{\mathrm {Vm} }}}
ε
r
{\displaystyle \varepsilon _{\mathrm {r} }\,}
E
N
=
|
E
→
|
⋅
cos
(
φ
)
{\displaystyle E_{\mathrm {N} }=|{\vec {E}}|\cdot \,\cos(\varphi )\,}
nach oben
Bearbeiten
Die elektrische Feldstärke ist eine vektorielle Größe; sie hat somit einen Betrag und eine Richtung.
E
→
Einheit:
V
m
bzw.
N
C
{\displaystyle {\vec {E}}\qquad {\text{Einheit:}}\,{\frac {\mathrm {V} }{\mathrm {m} }}\quad {\text{bzw.}}\quad {\frac {\mathrm {N} }{\mathrm {C} }}}
Die Einheiten veranschaulichen die einfachste Berechnungen des E-Feldes:
E
→
=
F
→
q
=
d
U
d
l
→
{\displaystyle {\vec {E}}={\frac {\vec {F}}{q}}={\frac {\mathrm {d} U}{\vec {\mathrm {d} l}}}}
Feldstärke im Potenzialfeld:
E
→
=
−
grad
(
φ
)
{\displaystyle {\vec {E}}=-\operatorname {grad} (\varphi )}
skalar:
E
=
1
4
π
ε
⋅
Q
r
2
mit
ε
=
ε
0
ε
r
{\displaystyle E={\frac {1}{4\pi \varepsilon }}\,\cdot \,{\frac {Q}{r^{2}}}\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }}
vektoriell:
E
→
=
1
4
π
ε
⋅
Q
r
2
⋅
r
→
r
mit
ε
=
ε
0
ε
r
{\displaystyle {\vec {E}}={\frac {1}{4\pi \varepsilon }}\,\cdot \,{\frac {Q}{r^{2}}}\,\cdot \,{\frac {\vec {r}}{r}}\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }}
ε
0
{\displaystyle \varepsilon _{0}}
=
8,854
18782
⋯
⋅
10
−
12
A
s
V
m
{\displaystyle =8{,}85418782\dots \cdot 10^{-12}\,{\frac {\mathrm {As} }{\mathrm {Vm} }}}
ε
r
{\displaystyle \varepsilon _{\mathrm {r} }}
äußeres Feld:
skalar:
E
=
Q
2
π
ε
l
r
=
ρ
2
π
ε
r
mit
ρ
=
Q
l
{\displaystyle E={\frac {Q}{2\pi \varepsilon lr}}={\frac {\rho }{2\pi \varepsilon r}}\quad {\text{mit}}\quad \rho ={\frac {Q}{l}}}
vektoriell:
E
→
(
P
)
=
Q
2
π
ε
l
(
p
→
×
e
l
→
)
2
⋅
(
e
l
→
×
(
p
→
×
e
l
→
)
)
=
ρ
2
π
ε
(
p
→
×
e
l
→
)
2
⋅
(
e
l
→
×
(
p
→
×
e
l
→
)
)
mit
e
l
→
=
l
→
|
l
→
|
,
p
→
=
O
P
→
{\displaystyle {\vec {E}}(P)={\frac {Q}{2\pi \varepsilon l({\vec {p}}\times {\vec {e_{l}}})^{2}}}\cdot ({\vec {e_{l}}}\times ({\vec {p}}\times {\vec {e_{l}}}))={\frac {\rho }{2\pi \varepsilon ({\vec {p}}\times {\vec {e_{l}}})^{2}}}\cdot ({\vec {e_{l}}}\times ({\vec {p}}\times {\vec {e_{l}}}))\quad {\text{mit}}\quad {\vec {e_{l}}}={\frac {\vec {l}}{|{\vec {l}}|}},\quad {\vec {p}}={\vec {OP}}}
inneres Feld:
Für eine Statische Ladungsverteilung muss die Summe aller Kräfte auf jede Ladung 0 sein. Da Ladungen im inneren eines Leiters frei beweglich sind gilt, darf es kein Feld geben. Diesem würde jede Ladung folgen, bis auftretende Ladungsverteilungen das Ursprungsfeld kompensieren. Das heißt, dass es keine Potentialdifferenz gibt:
Δ
U
=
0
{\displaystyle \Delta U=0}
U
(
r
→
)
=
const.
{\displaystyle U({\vec {r}})={\text{const.}}}
E
→
(
r
→
)
=
−
∇
U
(
r
→
)
=
0
{\displaystyle {\vec {E}}({\vec {r}})=-\nabla U({\vec {r}})=0}
Nach dem Eindeutigkeitssatz, ist dies die richtige Lösung. nach oben
Bearbeiten
U
Einheit ist Volt:
V
=
J
C
{\displaystyle U\qquad {\text{Einheit ist Volt: }}\mathrm {V} ={\frac {\mathrm {J} }{\mathrm {C} }}}
φ
Einheit:
V
{\displaystyle \varphi \qquad {\text{Einheit: }}\mathrm {V} }
Spannung zwischen zwei Punkten im E-Feld
Bearbeiten
U
A
B
=
W
A
B
q
{\displaystyle U_{AB}={\frac {W_{AB}}{q}}}
U
A
B
=
∫
A
B
E
→
⋅
d
s
→
{\displaystyle U_{AB}=\int \limits _{A}^{B}{{\vec {E}}\cdot {\vec {\mathrm {d} s}}}}
im homogenen Feld:
U
A
B
=
E
→
⋅
s
→
{\displaystyle U_{AB}={\vec {E}}\cdot {\vec {s}}}
φ
A
=
U
A
Z
=
−
∫
Z
A
E
→
⋅
d
s
→
{\displaystyle \varphi _{A}=U_{AZ}=-\int \limits _{Z}^{A}{{\vec {E}}\cdot {\vec {\mathrm {d} s}}}}
Z
{\displaystyle Z}
φ
Z
=
0
{\displaystyle \varphi _{Z}=0}
Wenn kein bewegendes Magnetischesfeld vorhanden ist.
∮
E
→
⋅
d
s
→
=
0
{\displaystyle \oint {\vec {E}}\cdot {\rm {d}}{\vec {s}}=0}
∮
E
→
⋅
d
s
→
=
−
∫
∂
B
→
∂
t
d
A
→
=
E
{\displaystyle \oint {\vec {E}}\cdot \mathrm {d} {\vec {s}}=-\int {\frac {\partial {\vec {B}}}{\partial t}}\mathrm {d} {\vec {A}}={\mathcal {E}}}
nach oben
die Kapazität ist ein Maß für die Speicherfähigkeit eines Kondensators . Ihr Symbolbuchstabe ist:
C
{\displaystyle C\ }
Ihre Einheit ist das Farad:
[
C
]
=
1
F
=
C
V
{\displaystyle [C]=1\,\mathrm {F} ={\frac {\mathrm {C} }{\mathrm {V} }}}
Die Einheit veranschaulicht die einfachste Berechnung der Kapazität:
C
=
Q
U
{\displaystyle C={\frac {Q}{U}}}
Bearbeiten
C
=
Q
U
=
∮
A
ε
E
(
A
)
→
⋅
d
A
→
∫
A
B
E
(
s
)
→
⋅
d
s
→
{\displaystyle C={\frac {Q}{U}}={\frac {\oint _{A}\varepsilon {\vec {E(A)}}\cdot d{\vec {A}}}{\int _{A}^{B}{\vec {E(s)}}\cdot d{\vec {s}}}}}
C
=
ε
A
d
mit
ε
=
ε
0
ε
r
{\displaystyle C=\varepsilon {\frac {A}{d}}\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }}
ε
{\displaystyle \varepsilon }
Permittivität (Dielektrizitätszahl)
ε
0
{\displaystyle \varepsilon _{0}}
elektrische Feldkonstante
=
8,854
18782
…
⋅
10
−
12
A
s
V
m
{\displaystyle =8{,}85418782\ldots \cdot 10^{-12}\,\mathrm {\frac {\mathrm {A} s}{\mathrm {V} m}} }
ε
r
{\displaystyle \varepsilon _{\mathrm {r} }}
könnte z.B. ein Koax-Kabel sein
C
=
2
π
ε
l
ln
r
a
r
i
mit
ε
=
ε
0
ε
r
{\displaystyle C={\frac {2\pi \varepsilon l}{\ln {\frac {r_{\mathrm {a} }}{r_{\mathrm {i} }}}}}\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }}
r
a
{\displaystyle r_{\mathrm {a} }}
r
i
{\displaystyle r_{\mathrm {i} }}
l
{\displaystyle l}
C
=
4
π
ε
r
mit
ε
=
ε
0
ε
r
{\displaystyle C=4\pi \varepsilon r\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }}
r
{\displaystyle r}
C
=
4
π
ε
(
1
r
i
−
1
r
a
)
m
i
t
ε
=
ε
0
ε
r
{\displaystyle C={\frac {4\pi \varepsilon }{\left({{\frac {1}{r_{\rm {i}}}}-{\frac {1}{r_{\rm {a}}}}}\right)}}\quad {\rm {mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\rm {r}}}
r
a
{\displaystyle r_{\mathrm {a} }}
r
i
{\displaystyle r_{\mathrm {i} }}
Im SI-System gilt:
Ampèresches Gesetz
∇
×
H
=
∂
D
∂
t
+
j
{\displaystyle \nabla \times \mathbf {H} ={\frac {\partial \mathbf {D} }{\partial t}}+\mathbf {j} }
Induktionsgesetz Faradaysches Gesetz
∇
×
E
=
−
∂
B
∂
t
{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
Coulombsches Gesetz
∇
⋅
D
=
ρ
{\displaystyle \nabla \cdot \mathbf {D} =\rho }
Gaußsches Gesetz des Magnetismus
∇
⋅
B
=
0
{\displaystyle \nabla \cdot \mathbf {B} =0}
Elektrische Flussdichte
D
=
ε
0
E
+
P
{\displaystyle \mathbf {D} =\varepsilon _{0}\,\mathbf {E} +\mathbf {P} }
Magnetische Flussdichte
B
=
μ
0
(
H
+
M
)
{\displaystyle \mathbf {B} =\mu _{0}\,(\mathbf {H} +\mathbf {M} )}
Wobei
H
{\displaystyle \mathbf {H} }
magnetische Feldstärke ,
B
{\displaystyle \mathbf {B} }
magnetische Flussdichte ,
E
{\displaystyle \mathbf {E} }
elektrische Feld ,
D
{\displaystyle \mathbf {D} }
elektrische Flussdichte ,
P
{\displaystyle \mathbf {P} }
Polarisation ,
M
{\displaystyle \mathbf {M} }
Magnetisierung ,
j
{\displaystyle \mathbf {j} }
Stromdichte und
ρ
{\displaystyle \rho }
Ladungsdichte ist
Für den stationären Fall gilt:
∇
⋅
j
=
−
∂
ρ
∂
t
{\displaystyle \nabla \cdot \mathbf {j} =-{\frac {\partial \rho }{\partial t}}}
Für isotrope Medien mit der Leitfähigkeit
σ
{\displaystyle \sigma }
j
=
σ
E
{\displaystyle \mathbf {j} =\sigma \mathbf {E} }
A
{\displaystyle \mathbf {A} }
Vektorpotential , mit dem man das
B
{\displaystyle \mathbf {B} }
B
=
∇
×
A
{\displaystyle \mathbf {B} =\nabla \times \mathbf {A} }
A
=
μ
0
4
π
∫
j
(
r
′
)
|
r
−
r
′
|
d
3
r
′
{\displaystyle \mathbf {A} ={\frac {\mu _{0}}{4\pi }}\int {\frac {\mathbf {j} (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'}
Φ
{\displaystyle \mathbf {\Phi } }
E
{\displaystyle \mathbf {E} }
E
=
−
∇
Φ
−
∂
A
∂
t
{\displaystyle \mathbf {E} =-\nabla \Phi -{\frac {\partial \mathbf {A} }{\partial t}}}
Φ
=
1
4
π
ε
0
∫
ρ
(
r
′
)
|
r
−
r
′
|
d
3
r
′
{\displaystyle \Phi ={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\rho (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'}
F
=
q
(
E
+
v
×
B
)
{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}
unter Vernachlässigung des E-Feldes folgt
F
=
∫
d
r
ρ
v
×
B
=
∫
d
r
j
×
B
{\displaystyle \mathbf {F} =\int d\mathbf {r} \rho \mathbf {v} \times \mathbf {B} =\int d\mathbf {r} \mathbf {j} \times \mathbf {B} }
L
j
m
=
μ
r
μ
0
4
π
∮
C
∮
D
d
r
⋅
d
r
′
|
r
−
r
′
|
=
L
m
j
{\displaystyle L_{jm}={\frac {\mu _{r}\mu _{0}}{4\pi }}\oint _{C}\oint _{D}{\frac {d\mathbf {r} \cdot d\mathbf {r} '}{|\mathbf {r} -\mathbf {r} '|}}=L_{mj}}
Um die inhomogene Wellengleichung zu lösen, benutzt man retardierende Potentiale .
Man erhält dann folgendes:
A
=
μ
0
4
π
∫
j
(
r
′
,
t
−
|
r
−
r
′
|
c
)
|
r
−
r
′
|
d
3
r
′
{\displaystyle \mathbf {A} ={\frac {\mu _{0}}{4\pi }}\int {\frac {\mathbf {j} (\mathbf {r} ',t-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}})}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'}
Φ
=
1
4
π
ε
0
∫
ρ
(
r
′
,
t
−
|
r
−
r
′
|
c
)
|
r
−
r
′
|
d
3
r
′
{\displaystyle \Phi ={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\mathbf {\rho } (\mathbf {r} ',t-{\frac {|\mathbf {r} -\mathbf {r} '|}{c}})}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'}
S
=
E
×
H
{\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} }
−
j
⋅
E
=
∂
w
∂
t
+
∇
⋅
S
{\displaystyle -\mathbf {j} \cdot \mathbf {E} ={\frac {\partial w}{\partial t}}+\nabla \cdot \mathbf {S} }
Energiedichte des elektromagnetischen Feldes
Bearbeiten
w
=
1
2
(
H
⋅
B
+
E
⋅
D
)
{\displaystyle w={\frac {1}{2}}(\mathbf {H} \cdot \mathbf {B} +\mathbf {E} \cdot \mathbf {D} )}
∇
⋅
A
+
1
c
2
∂
Φ
∂
t
=
0
{\displaystyle \nabla \cdot \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \Phi }{\partial t}}=0}
◻
A
=
−
μ
0
j
{\displaystyle \Box \mathbf {A} =-\mu _{0}\mathbf {j} }
◻
Φ
=
−
ρ
ε
0
{\displaystyle \Box \Phi =-{\frac {\rho }{\varepsilon _{0}}}}
∇
⋅
A
=
0
{\displaystyle \nabla \cdot \mathbf {A} =0}
◻
A
=
−
μ
0
j
−
1
c
∂
E
∂
t
{\displaystyle \Box \mathbf {A} =-\mu _{0}\mathbf {j} -{\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}}
∇
2
Φ
=
−
ρ
ε
0
{\displaystyle \nabla ^{2}\Phi =-{\frac {\rho }{\varepsilon _{0}}}}
◻
{\displaystyle \Box }
d'Alembertoperator ist.
Energiebilanz für emittiertes oder absorbiertes Licht
Δ
E
=
E
n
−
E
m
{\displaystyle \Delta E=E_{n}-E_{m}\,}
Δ
E
=
h
⋅
f
{\displaystyle \Delta E=h\cdot f}
E
n
,
E
m
{\displaystyle E_{n},E_{m}}
f
{\displaystyle f}
h
{\displaystyle h}
h
=
6,626
08
⋅
10
−
34
k
g
⋅
m
2
s
{\displaystyle h=6{,}62608\cdot 10^{-34}{\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} }}}
Spektralserien des
1
λ
=
R
H
⋅
(
1
n
2
−
1
m
2
)
{\displaystyle {\frac {1}{\lambda }}=R_{H}\cdot \left({\frac {1}{n^{2}}}-{\frac {1}{m^{2}}}\right)}
f
=
R
y
⋅
(
1
n
2
−
1
m
2
)
|
n
<
m
{\displaystyle f=R_{y}\cdot \left({\frac {1}{n^{2}}}-{\frac {1}{m^{2}}}\right)\qquad |n<m}
λ
{\displaystyle \lambda \,}
R
H
{\displaystyle R_{H}}
R
H
=
1,097
37315
⋅
10
7
m
−
1
{\displaystyle R_{H}=1{,}09737315\cdot 10^{7}\mathrm {m} ^{-1}}
R
y
{\displaystyle R_{y}\,}
R
y
=
3,289
84195
⋅
10
15
H
z
{\displaystyle R_{y}=3{,}28984195\cdot 10^{15}\mathrm {Hz} }
Relative Atommasse
A
r
=
m
A
u
{\displaystyle A_{\mathrm {r} }={\frac {m_{\mathrm {A} }}{\mathrm {u} }}}
m
A
{\displaystyle m_{\mathrm {A} }}
1
u
=
1,660
540
⋅
10
−
27
k
g
{\displaystyle 1\,\mathrm {u} =1{,}660540\cdot 10^{-27}\,\mathrm {kg} }
Nukleonenzahl
A
=
Z
+
N
{\displaystyle A=Z+N}
X
{\displaystyle X}
Z
{\displaystyle Z}
A
{\displaystyle A}
N
{\displaystyle N}
m
p
{\displaystyle m_{p}}
m
p
=
1,672
6231
⋅
10
−
27
k
g
{\displaystyle m_{p}=1{,}6726231\cdot 10^{-27}\,\mathrm {kg} }
m
n
{\displaystyle m_{n}}
m
n
=
1,674
9286
⋅
10
−
27
k
g
{\displaystyle m_{n}=1{,}6749286\cdot 10^{-27}\,\mathrm {kg} }
c
{\displaystyle c}
c
=
2,997
92458
⋅
10
8
m
s
{\displaystyle c=2{,}99792458\cdot 10^{8}{\frac {\mathrm {m} }{\mathrm {s} }}}
Symbolschreibweise
Z
A
X
{\displaystyle {}_{Z}^{A}X}
Kernmasse
m
K
{\displaystyle m_{\mathrm {K} }}
Δ
m
{\displaystyle \Delta m}
m
K
<
Z
⋅
m
p
+
N
⋅
m
n
{\displaystyle m_{\mathrm {K} }<Z\cdot m_{p}+N\cdot m_{n}}
Δ
m
=
(
Z
⋅
m
p
+
N
⋅
m
n
)
−
m
K
{\displaystyle \Delta m=\left(Z\cdot m_{p}+N\cdot m_{n}\right)-m_{\mathrm {K} }}
Kernbindungsenergie
E
B
=
Δ
m
⋅
c
2
{\displaystyle E_{\mathrm {B} }=\Delta m\cdot c^{2}}
Die Formelsammlung Kernwaffenexplosion ist ein Teil der Formelsammlung , in der auch Formeln zu anderen Fachbereichen zu finden sind.
Bearbeiten
DNA-Standardkurve für OP und DP Der von der früheren US-Behörde Defense Nuclear Agency (DNA) entwickelte Standardkurve für die Druckwelle einer 1-Kilotonnen -Explosion liegt die folgende Beziehung zwischen dem Abstand R vom Explosionszentrum und dem Druckpegel OP zugrunde, wobei von einer Freiluftexplosion in einer homogenen unbegrenzten Atmosphäre unter Meeresniveaubedingungen (P = P 0 = 101325 Pa und T = T 0 = 288,15 K ) ausgegangen wird:
O
P
D
N
A
=
3.04
×
10
11
R
3
+
1.13
×
10
9
R
2
+
7.9
×
10
6
R
ln
(
R
445.42
+
3
exp
(
−
1
3
R
445.42
)
)
{\displaystyle {\begin{matrix}{\mathit {OP}}_{\mathrm {DNA} }&=&{\frac {3.04\times 10^{11}}{R^{3}}}+{\frac {1.13\times 10^{9}}{R^{2}}}\\&&\\&&+\quad {\frac {7.9\times 10^{6}}{R{\sqrt {\ln \left({\frac {R}{445.42}}+3\exp \left(-{\frac {1}{3}}{\sqrt {\frac {R}{445.42}}}\right)\right)}}}}\end{matrix}}}
Dabei ist R in m einzusetzen (der Übersichtlichkeit wegen wurde auf die Einheiten-Divisoren in der Formel verzichtet), und das Ergebnis ist OP in Pa. Der dynamische Druck ergibt sich aus
D
P
=
n
−
1
2
O
P
,
{\displaystyle {\mathit {DP}}={\frac {n-1}{2}}\,{\mathit {OP}}\,,}
wobei n das Dichteverhältnis vor und hinter der Stoßfront und P der Druck der ungestörten Atmosphäre ist. Für Luft ist
n
=
1
+
μ
s
(
O
P
P
+
1
)
μ
+
(
O
P
P
+
1
)
mit
μ
=
κ
+
1
κ
−
1
und
μ
s
=
κ
s
+
1
κ
s
−
1
.
{\displaystyle n={\frac {1+\mu _{\mathrm {s} }\left({\frac {\mathrm {OP} }{P}}+1\right)}{\mu +\left({\frac {\mathrm {OP} }{P}}+1\right)}}\quad {\mbox{mit}}\quad \mu ={\frac {\kappa +1}{\kappa -1}}\quad {\mbox{und}}\quad \mu _{\mathrm {s} }={\frac {\kappa _{\mathrm {s} }+1}{\kappa _{\mathrm {s} }-1}}\,.}
κ ist der Adiabatenexponent , und der Index s deutet an. dass κ infolge der Stoßerhitzung hinter der Stoßfront nicht mehr den klassischen Wert für Luft von 1,402 besitzt, da durch Ionisation mehr Freiheitsgrade hinzukommen. Unterhalb von etwa 1000 kPa ist der Korrekturterm vernachlässigbar; für höhere Drucke Für werden zunächst einige temporäre Variablen benötigt, über die dann die Korrektur für κ resultiert:
x
=
O
P
P
+
1
;
y
=
10
−
12
x
6
;
z
=
ln
x
−
0
,
47
y
100
+
y
{\displaystyle x={\frac {\mathit {OP}}{P}}+1\,;\quad y=10^{-12}\,x^{6}\,;\quad z=\ln x-{\frac {0{,}47y}{100+y}}}
Dann ist
κ
s
=
1,402
−
3
,
4
×
10
−
4
z
4
1
+
2
,
22
×
10
−
5
z
6
.
{\displaystyle \kappa _{\mathrm {s} }=1{,}402-{\frac {3{,}4\times 10^{-4}\,z^{4}}{1+2{,}22\times 10^{-5}\,z^{6}}}\,.}
Aus den hier berechneten Größen folgt auch der Normalreflexionsfaktor F n , der die Druckerhöhung bei senkrechter Reflexion wiedergibt (trivialerweise 2 bei gewöhnlichen Schallwellen):
F
n
=
2
+
(
κ
s
+
1
)
(
n
−
1
)
2
{\displaystyle F_{\mathrm {n} }=2+{\frac {(\kappa _{\mathrm {s} }+1)(n-1)}{2}}}
Mit diesen Resultaten ergibt sich aus den Rankine-Hugoniot-Gleichungen die Ausbreitungsgeschwindigkeit und die Windgeschwindigkeit der Stoßfront:
v
s
=
c
s
⋅
(
κ
s
+
1
)
O
P
D
N
A
2
κ
s
P
+
1
;
c
s
=
Schallgeschwindigkeit
{\displaystyle v_{\mathrm {s} }=c_{\mathrm {s} }\cdot {\sqrt {{\frac {(\kappa _{\mathrm {s} }+1){\mathit {OP}}_{\mathrm {DNA} }}{2\kappa _{\mathrm {s} }P}}+1}}\ ;\quad c_{\mathrm {s} }={\mbox{Schallgeschwindigkeit}}}
w
s
=
v
s
⋅
(
1
−
1
n
)
{\displaystyle w_{\mathrm {s} }=v_{\mathrm {s} }\cdot \left(1-{\frac {1}{n}}\right)}
Daraus ergibt sich durch Integration der reziproken Geschwindigkeit auch die Laufzeit der Druckwelle zu einem bestimmten Radius.
Der wichtigste Skalierungsfaktor ist die Sprengkraft- oder Sachs -Skalierung. Die Standardkurven sind für 1 kT definiert; für beliebige Energien W (gleicher mechanischer Anteil vorausgesetzt) ist für beliebige Längen- und Zeitgrößen S die Gleichung
S
(
W
)
=
S
(
1
k
T
)
⋅
(
W
k
T
)
1
/
3
{\displaystyle S(W)=S(1\,\mathrm {kT} )\cdot \left({W \over \mathrm {kT} }\right)^{1/3}}
anzuwenden. Dabei ist W bereits ein auf den typischen mechanischen Anteil von Atomwaffen (etwa 50 bis 60 Prozent der Gesamtenergie) normiert. Für andere als nukleare Explosionen muss um das Verhältnis der mechanischen Anteile ξ korrigiert werden. Nimmt man den Mittelwert 55 % als Referenzwert für Nuklearexplosionen, so gilt für eine Explosion mit Energie E und mechanischem Anteil ξ
W
=
ξ
0
,
55
⋅
E
.
{\displaystyle W={\frac {\xi }{0{,}55}}\cdot E\ .}
Für chemische Explosionen kann näherungsweise ξ = 1 gesetzt werden. Für gegebenen Luftdruck P und Temperatur T gehen zudem
S
P
=
P
P
0
;
S
T
=
T
T
0
;
{\displaystyle S_{P}={\frac {P}{P_{0}}}\ ;\quad S_{T}={\frac {T}{T_{0}}}\ ;}
L
a
¨
n
g
e
:
S
L
=
S
P
−
1
/
3
;
Dauer:
S
D
=
S
L
S
T
{\displaystyle \mathrm {L{\ddot {a}}nge:} \ S_{L}=S_{P}^{-1/3}\ ;\quad {\text{Dauer:}}\ S_{D}={\frac {S_{L}}{\sqrt {S_{T}}}}}
in die korrigierte 1-kT-Druck- und Zeitkurve ein:
O
P
(
R
,
P
)
=
S
P
⋅
O
P
(
R
/
S
L
,
P
0
)
;
t
(
R
,
P
,
T
)
=
S
D
⋅
t
(
R
/
S
L
,
P
0
,
T
0
)
.
{\displaystyle {\mathit {OP}}(R,P)=S_{P}\cdot {\mathit {OP}}(R/S_{L},P_{0})\ ;\quad t(R,P,T)=S_{D}\cdot t(R/S_{L},P_{0},T_{0})\ .}
Der Zeitskalierungsfaktor ist für die Laufzeit der Druckwelle von Bedeutung. Über Druck bzw. Temperatur wird auch die weiter unten benötigte Schallgeschwindigkeit skaliert.
Sind Explosionszentrum und Ziel auf unterschiedlichen Höhen, so zeigen Beobachtungswerte und theoretische Rechnungen, dass für den Druck die Skalierungsfaktoren für die Höhe des Zieles statt des Explosionsherdes zu wählen sind. Für die Laufzeit sind die Verhältnisse komplizierter. Zusätzlich ist zu beachten, dass der mechanische Wirkungsgrad bei geringer Dichte kleiner wird. In etwa 30 km Höhe liegt er noch zwischen 30 % und 40 % (Glasstone, Dolan, The Effects of Nuclear Weapons ,1977; kurz EoNW77), in größeren Höhen nimmt er dann rapide ab.
Abb. 2: Abhängigkeit der Isobaren-Radien von der Detonationshöhe Das DNA-Modell beschreibt auch die Druckwelle bei Luftexplosionen, also unter Berücksichtigung der Reflexion an der Oberfläche. Bei der Berechnung sind zwei Regime zu unterscheiden, nämlich das Regime der regulären Reflexion und das der Mach-Reflexion. Für das erstere benötigt man neben dem oben berechneten Normalreflexionsfaktor
Rn noch einige temporäre Variablen und Koeffizienten, um dann den Überdruck für reguläre Reflexion, OP reg berechnen zu können. Dabei wurde gelegentlich von Druckgrößen nur der Betrag verwendet (z. B. in Exponenten oder bei nicht-ganzzahliger Potenzierung usw.), der Übersichtlichkeit wegen aber auf zusätzliche Symbole verzichtet.
Seien H und GR für eine 1-kT-Explosion gegeben. Dann sind die Raumdiagonale R der Einfallswinkel α der Primärfront sowie einige temporäre Variablen wie folgt definiert:
R
=
H
2
+
G
R
2
;
α
=
arctan
H
G
R
{\displaystyle R={\sqrt {H^{2}+{\mathit {GR}}^{2}}}\ ;\quad \alpha =\arctan {\frac {H}{\mathit {GR}}}}
T
=
340
O
P
D
N
A
0
,
55
;
U
=
(
7782
O
P
D
N
A
0
,
7
+
0
,
9
)
−
1
{\displaystyle T={\frac {340}{OP_{\mathrm {DNA} }^{0{,}55}}}\ ;\quad U=\left({\frac {7782}{OP_{\mathrm {DNA} }^{0{,}7}}}+0{,}9\right)^{-1}}
U
~
=
(
7473
O
P
D
N
A
0
,
5
+
6
,
6
)
−
1
;
V
=
(
647
O
P
D
N
A
0
,
8
+
U
~
)
−
1
{\displaystyle {\tilde {U}}=\left({\frac {7473}{OP_{\mathrm {DNA} }^{0{,}5}}}+6{,}6\right)^{-1}\ ;\quad V=\left({\frac {647}{OP_{\mathrm {DNA} }^{0{,}8}}}+{\tilde {U}}\right)^{-1}}
Grenzwinkel α M zwischen regulärer und Mach-Region und (Winkel-)Breite
β der Zone, wo die Wellen verschmelzen, Hilfsvariablen und Schaltparameter σ :
α
M
=
arctan
1
T
+
U
;
β
=
arctan
1
T
+
V
;
s
=
α
−
α
M
β
{\displaystyle \alpha _{\mathrm {M} }=\arctan {\frac {1}{T+U}}\ ;\quad \beta =\arctan {\frac {1}{T+V}}\ ;\quad s={\frac {\alpha -\alpha _{\mathrm {M} }}{\beta }}}
s
0
=
max
(
min
(
s
,
1
)
,
−
1
)
;
σ
=
0
,
5
(
sin
(
π
2
s
0
)
+
1
)
{\displaystyle s_{0}=\max(\min(s,1),-1)\ ;\quad \sigma =0{,}5\left(\sin \left({\frac {\pi }{2}}\,s_{0}\right)+1\right)}
Ausgangspunkt ist die DNA-Standardfunktion, die auf die Raumentfernung R angewendet wird
f
=
O
P
D
N
A
(
R
)
75842
P
a
;
g
=
f
6
(
1
,
2
+
0
,
07
f
0
,
5
)
f
6
+
1
,
{\displaystyle f={\frac {OP_{\mathrm {DNA} }(R)}{75842\,\mathrm {Pa} }}\ ;\quad g={\frac {f^{6}\left(1{,}2+0{,}07\,f^{0{,}5}\right)}{f^{6}+1}}\ ,}
und daraus
O
P
r
e
g
=
O
P
D
N
A
⋅
(
(
F
n
−
2
)
sin
g
α
+
2
)
.
{\displaystyle OP_{\mathrm {reg} }=OP_{\mathrm {DNA} }\cdot \left((F_{\mathrm {n} }-2)\sin ^{g}\alpha +2\right)\ .}
Ein Speziallfall ist die Situation im Hypozentrum:
O
P
G
Z
=
F
n
⋅
O
P
D
N
A
;
H
>
0
{\displaystyle {\mathit {OP}}_{\mathrm {GZ} }=F_{\mathrm {n} }\cdot {\mathit {OP}}_{\mathrm {DNA} }\ ;\quad H>0}
Zunächst wieder ein paar Zwischenvariablen:
A
=
min
(
3
,
7
−
0
,
94
ln
(
G
R
)
,
0
,
7
)
;
B
=
0
,
77
ln
(
G
R
)
−
18
G
R
−
3
,
8
{\displaystyle A=\min(3{,}7-0{,}94\,\ln({\mathit {GR}}),\ 0{,}7)\ ;\quad B=0{,}77\,\ln({\mathit {GR}})-{\frac {18}{\mathit {GR}}}-3{,}8}
C
=
max
(
A
,
B
)
{\displaystyle C=\max(A,B)}
Nun setze 2^(-1/3)*GR anstelle von R in die DNA-Formel OP (R ) ein und setze das
daraus erhaltene Ergebnis OP 1 hier ein:
O
P
m
a
c
h
=
O
P
1
1
−
C
sin
α
{\displaystyle {\mathit {OP}}_{\mathrm {mach} }={\frac {{\mathit {OP}}_{1}}{1-C\sin \alpha }}}
Der Abstand GR M , an dem die Verschmelzung von direkter und reflektierter Welle einsetzt, lässt sich auch annähern durch
G
R
M
=
H
2
,
5
5822
+
2
,
09
H
0
,
75
.
{\displaystyle GR_{\mathrm {M} }={\frac {H^{2{,}5}}{5822}}+2{,}09\,H^{0{,}75}\ .}
Der Gesamt-Überdruck OP air ist dann
O
P
a
i
r
=
σ
O
P
r
e
g
+
(
1
−
σ
)
O
P
m
a
c
h
.
{\displaystyle OP_{\mathrm {air} }=\sigma OP_{\mathrm {reg} }+(1-\sigma )OP_{\mathrm {mach} }\ .}
Der dynamische Druck folgt dann mit dem Dichteverhältnis in der resultierenden Druckfront
(anstelle der Standarddruckwelle) na =n (OP air ):
D
P
a
i
r
=
O
P
a
i
r
(
n
a
−
1
)
(
1
−
σ
sin
2
α
)
/
2
{\displaystyle DP_{\mathrm {air} }=OP_{\mathrm {air} }(n_{a}-1)\left(1-\sigma \sin ^{2}\alpha \right)/2}
Die Berechnung der Ausbreitungsgeschwindigkeit der Welle kann nun mit OP air statt OP DNA geschehen; die Windgeschwindigkeit w s berechnet man sinnvollerweise aus DP air , weil dort die Restriktion auf die Horizontale bereits berücksichtigt worden ist:
w
s
=
2
D
P
a
i
r
ρ
2
,
{\displaystyle w_{s}={\sqrt {2{\frac {{\mathit {DP}}_{\mathrm {air} }}{\rho _{2}}}}}\ ,}
wobei ρ 2 = n ρ 0 die Dichte hinter der Stoßfront ist.
Um die Laufzeit der Druckwelle zu errechnen, ist die reziproke Geschwindigkeit der Stoßfront über die (auf die tatsächliche Sprengkraft skalierte) Entfernung zu integrieren. Bei Luftexplosionen sind hier zwei Wegabschnitte zu unterscheiden:
Innerhalb der Mach-Zone GR M ist die Laufzeit mit der einer Freiluftexplosion (skalierte DNA-Standardexplosion) identisch. Für R ist dabei die Raumdiagonale vom Explosionszentrum zum Messpunkt einzusetzen. Die Refraktion der Welle in der inhomogenen Atmosphäre kann normalerweise vernachlässigt und von einer geradlinigen Ausbreitung ausgegangen werden.
Außerhalb der Mach-Zone bewegt sich die Stoßfront horizontal, daher ist erst die Strecke vom Zentrum zum Rand des Mach-Radius als Freiluftexplosion und von dort zum Messpunkt als Bodenexplosion mit der reflexionsverstärkten Druckwelle zu betrachten, die sich schneller fortpflanzt als die unverstärkte Welle. Das DNA-Modell verwendet einen Näherungsfit, der ohne rechenaufwendige Integration auskommt. Zunächst wird eine Laufzeitfunktion für eine 1-kT-Freiluftexplosion definiert:
t
f
r
e
e
(
R
)
=
R
2
(
R
+
6
,
7
)
340
,
5
R
2
+
73200
R
+
7
,
12
⋅
10
6
{\displaystyle t_{\mathrm {free} }(R)={\frac {R^{2}(R+6{,}7)}{340{,}5\,R^{2}+73200\,R+7{,}12\cdot 10^{6}}}}
Für Freiluftexplosionen müssen jetzt nur R und t free um die Kubikwurzel von W /kT skaliert werden. Für Luftexplosionen wird ein weiterer Korrekturfaktor benötigt:
ν
=
{
1
wenn
G
R
≤
G
R
M
2
3
+
(
1
−
2
3
)
G
R
M
G
R
sonst
{\displaystyle \nu =\left\{{\begin{matrix}1&{\mbox{wenn}}\ GR\leq GR_{\mathrm {M} }\\{\sqrt[{3}]{2}}+\left(1-{\sqrt[{3}]{2}}\right){\frac {GR_{\mathrm {M} }}{GR}}&{\mbox{sonst}}\end{matrix}}\right.}
Nun wird in die Laufzeitformel einfach Rν =R /ν statt R eingesetzt und das Ergebnis mit W ^(1/3) skaliert:
t
a
i
r
(
H
,
G
R
)
=
t
f
r
e
e
(
R
ν
)
,
t
a
i
r
,
W
(
G
R
)
=
t
a
i
r
(
G
R
)
⋅
(
W
k
T
)
1
/
3
{\displaystyle t_{\mathrm {air} }({\mathit {H}},{\mathit {GR}})=t_{\mathrm {free} }(R_{\nu })\ ,\quad t_{\mathrm {air} ,W}({\mathit {GR}})=t_{\mathrm {air} }({\mathit {GR}})\cdot \left({\frac {W}{\mathrm {kT} }}\right)^{1/3}}
Für von den Standardbedingungen stark abweichende Bedingungen können die obigen Skalierungsfaktoren auch für Luftexplosionen angewendet werden. Für große Detonationshöhen muss die numerische Integration mit anhand lokaler Längen- und Zeitskalierungen korrigierter Ausbreitungsgeschwindigkeit verwendet werden.
Auch diese Formeln sind durchweg für 1 kT Sprengkraft gegeben und können wie die übrigen
durch das Kubikwurzelgesetz skaliert werden.
Wieder sind zunächst einige Hilfsgrößen zu definieren, zunächst eine Zeitskalierung:
t
0
=
ln
(
1000
t
a
i
r
)
3
,
77
{\displaystyle t_{0}={\frac {\ln(1000\,t_{\mathrm {air} })}{3{,}77}}}
Dann ist die Dauer der 1-kT-Überdruckphase am Boden
D
p
,
s
u
r
f
=
0,001
⋅
(
155
exp
(
−
20
,
8
t
a
i
r
)
+
exp
(
−
t
0
2
+
4
,
86
t
0
+
0
,
25
)
)
{\displaystyle D_{p,\mathrm {surf} }=0{,}001\cdot \left(155\exp(-20{,}8\,t_{\mathrm {air} })+\exp \left(-t_{0}^{2}+4{,}86\,t_{0}+0{,}25\right)\right)}
aus der ein „Rohwert“ für die Überdruckdauer bei Luftexplosionen
D
p
,
u
n
m
o
d
=
D
p
,
s
u
r
f
(
1
−
F
A
F
B
)
{\displaystyle D_{p,\mathrm {unmod} }=D_{p,\mathrm {surf} }\,\left(1-F_{A}\,F_{B}\right)}
gewonnen wird, wobei
F
A
=
1
−
1
1
+
4
,
5
⋅
10
−
8
H
7
,
F
B
=
0
,
04
+
0
,
61
1
+
t
a
i
r
1
,
5
0,027
{\displaystyle F_{A}=1-{\frac {1}{1+4{,}5\cdot 10^{-8}\,H^{7}}}\ ,\quad F_{B}=0{,}04+{\frac {0{,}61}{1+{\frac {t_{\mathrm {air} }^{1{,}5}}{0{,}027}}}}}
Für beliebige Explosionshöhen für 1 kT Energie ist dann
D
p
=
D
p
,
u
n
m
o
d
(
1
,
16
exp
(
−
[
H
0,304
8
−
156
1062
]
)
)
{\displaystyle D_{p}=D_{p,\mathrm {unmod} }\left(1{,}16\,\exp \left(-\left[{\frac {{\frac {H}{0{,}3048}}-156}{1062}}\right]\right)\right)}
Obige Formeln gelten für den Überdruck . Die Dauer der positiven dynamischen Druckphase ist infolge der Massenträgheit der Luft in der Regel etwas länger als die der Überdruckphase
Für die folgende Berechnung der dynamischen Druckdauer sollte der GR den Wert
max
(
G
R
M
,
80
m
)
{\displaystyle \max(GR_{M},80\,\mathrm {m} )}
nicht unterschreiten.
H
f
t
≡
H
s
0,304
8
{\displaystyle H_{\mathrm {ft} }\equiv {\frac {H_{\mathrm {s} }}{0{,}3048}}}
und
R
f
t
≡
G
R
s
0,304
8
{\displaystyle R_{\mathrm {ft} }\equiv {\frac {GR_{\mathrm {s} }}{0{,}3048}}}
sowie
H
x
=
|
H
f
t
−
200
|
+
200
R
x
=
R
f
t
−
1000
D
q
0
=
0
,
3
+
0
,
42
exp
(
−
H
x
131
)
{\displaystyle {\begin{matrix}H_{x}&=&\left|H_{\mathrm {ft} }-200\right|+200\\R_{x}&=&R_{\mathrm {ft} }-1000\\D_{q0}&=&0{,}3+0{,}42\exp \left(-{\frac {H_{x}}{131}}\right)\end{matrix}}}
und
D
q
x
=
{
D
q
0
+
4
,
4
⋅
10
−
5
R
x
falls
R
x
>
0
D
q
0
+
R
x
⋅
F
C
sonst
{\displaystyle D_{qx}={\begin{cases}D_{q0}+4{,}4\cdot 10^{-5}R_{x}&\quad {\text{falls}}\,R_{x}>0\\D_{q0}+R_{x}\cdot F_{C}&\quad {\text{sonst}}\end{cases}}}
mit
F
C
=
1
2361
−
(
H
x
−
533
)
2
7
,
88
⋅
10
7
{\displaystyle F_{C}={\frac {1}{2361}}-{\frac {(H_{x}-533)^{2}}{7{,}88\cdot 10^{7}}}}
Die auf 1 kT skalierte dynamische positive Phasendauer ist dann
D
q
=
{
D
q
x
falls
H
f
t
≥
200
D
q
x
(
1
+
0
,
2
sin
π
H
f
t
200
)
sonst
{\displaystyle D_{q}={\begin{cases}D_{qx}&\quad {\text{falls}}\,H_{\mathrm {ft} }\geq 200\\D_{qx}\left(1+0{,}2\sin {\frac {\pi \,H_{\mathrm {ft} }}{200}}\right)&\quad {\text{sonst}}\end{cases}}}
Im Falle einer Explosion direkt am Boden vereinfacht sich die Beziehung für die Reflexion dergestalt, dass die halbkugelförmige Druckwelle sich wie eine Freiluftexplosion doppelter Sprengkraft verhält. In diesem Fall ist also
O
P
(
r
)
=
O
P
D
N
A
(
r
/
2
3
)
.
{\displaystyle {\mathit {OP}}(r)={\mathit {OP}}_{\mathrm {DNA} }(r/{\sqrt[{3}]{2}})\ .}
Die Entfernung von der Bodenexplosion, in der ein bestimmter Druck OP angenommen wird, kann alternativ zum numerischen Lösen näherungsweise auch durch folgenden Fit bestimmt werden:
G
R
O
P
,
H
=
0
m
≈
(
(
2,738
⋅
10
6
O
P
P
a
−
0,879
)
1
,
37
+
(
1,012
⋅
10
4
O
P
P
a
−
0,342
)
1
,
37
)
1
/
1
,
37
.
{\displaystyle {{\mathit {GR}}_{{\mathit {OP}},H=0} \over \mathrm {m} }\approx \left(\left(2{,}738\cdot 10^{6}\,{{\mathit {OP}} \over \mathrm {Pa} }^{-0{,}879}\right)^{1{,}37}+\left(1{,}012\cdot 10^{4}\,{{\mathit {OP}} \over \mathrm {Pa} }^{-0{,}342}\right)^{1{,}37}\right)^{1/1{,}37}\,.}
Diese Näherung für eine 1-kT-Explosion ist – in Bezug auf das Originalmodell – zwischen 0,3 und 10000 PSI (2,1 und 69000 kPa) auf ±1 % genau. Allerdings gilt diese Rechnung nur für einen Reflexionsgrad von 100 %. Kernwaffentests in Nevada und im Pazifik zeigten einen Reflexionsgrad von nur etwa 70 % für Wüstensand oder weichen feuchten Untergrund. Statt des doppelten ist hier also der 1,7-fache Wert der Freiluftsprengkraft einzusetzen. Der Radius verringert sich gemäß der Kubikwurzelregel. Für Luftdetonationen über Stadtgebieten, wo die Druckwelle Energie durch Zerstörungsarbeit verliert, gilt vermutlich etwas Ähnliches. Jedoch sind genaue Daten hierzu bisher nicht veröffentlicht worden.
Die Explosionshöhe, bei der der Grundradius GR OP OP maximal wird, ist näherungsweise gegeben durch die Beziehung:
H
O
P
m
≈
16100
(
O
P
P
a
)
−
0
,
38
=
560
(
O
P
P
S
I
)
−
0
,
38
.
{\displaystyle {H_{\mathit {OP}} \over \mathrm {m} }\approx 16100\,\left({{\mathit {OP}} \over \mathrm {Pa} }\right)^{-0{,}38}=560\,\left({{\mathit {OP}} \over \mathrm {PSI} }\right)^{-0{,}38}\,.}
Der durch diese Wahl von HOP maximierte Radius GROP ist dann ungefähr
G
R
O
P
m
≈
(
(
9
,
54
⋅
10
−
3
H
O
P
m
1
,
95
)
4
+
(
3
,
01
H
O
P
m
0
,
75
)
4
)
1
/
4
.
{\displaystyle {{\mathit {GR}}_{\mathit {OP}} \over \mathrm {m} }\approx \left(\left(9{,}54\cdot 10^{-3}\,{H_{\mathit {OP}} \over \mathrm {m} }^{1{,}95}\right)^{4}+\left(3{,}01\,{H_{\mathit {OP}} \over \mathrm {m} }^{0{,}75}\right)^{4}\right)^{1/4}\,.}
Diese Formeln sind in Bezug auf das Originalmodell auf ±20 % für H und ±10 % für GR im Bereich von 0,1 bis 10000 PSI (0,69 bis 69000 kPa) jedoch unter Vernachlässigung der atmosphärischen Druckvariation und für ebenes Gelände). Die Näherung ist allerdings ein Kompromiss zwischen dem BLAST-Modell und Daten aus EoNW77. Die Abweichungen vom BLAST-Modell resultieren überwiegend aus den Abweichungen beider Quelldaten.
Das DNA-Modell ist in weiten Bereichen von Radius und Druck gültig. Räumliche Modellgrenzen skalieren wie alle übrigen Längenskalen mit der Kubikwurzel der Sprengkraft.
Eingabewerte
Minimum
Maximum
Sprengkraft W / kT
0,1
25.000
Höhe in Standardatmosphäre / m
0
25.000
Höhe über Grund / m
0
4000 SL W 1/3
Ohne Reflexion: Radius R / m
16 SL W 1/3
4000 SL W 1/3
Mit Reflexion: Grundradius GR / m
LM
4000 SL W 1/3
H / m für dynamische Druckdauer
0
750 SL W 1/3
GR / m für dynamische Druckdauer
LQ
4000 SL W 1/3
Dabei ist LM = 20 SL W 1/3 , falls H < 25 SL W 1/3 und 0 sonst, sowie
LQ = max(GR M ,80 m). Die Modellgrenzen für die statische Überdruckphasendauer sind die gleichen wie für den statischen Überdruck selbst.
Diese Grenzen sind recht konservativ gewählt; plausible Ergebnisse liefert das Modell, mit Ausnahme der dynamischen Phasendauer, noch in mehr als dem Doppelten der oberen Radiusgrenze, wenn nahezu ideale Bedingungen vorausgesetzt werden. Die W -Skalierung beispielsweise ist theoretisch unbegrenzt und exakt gültig; die Grenzen ergeben sich vor allem aus dem Druckgradienten der Atmosphäre und den spezifischen Eigenschaften von Atomwaffen , auf die sich das Modell ursprünglich bezieht.
Die Genauigkeit des Modells hängt stark von der Genauigkeit der Messwerte zusammen, für die keine Angaben verfügbar sind. Abweichungen in Folge von nicht vorhersagbaren Umwelteinflüssen (Geländeformation, Winde, lokale Temperaturschwankungen usw.) sowie Unsicherheit bei der gemessenen Sprengkraft führen zu teilweise erheblichen Fehlern. Für große Distanzen können Reflexion und Refraktion zu lokaler Bündelung von Wellenfronten und damit zu erheblich größeren Druckspitzen führen. Daher wird zudem der zumeist erheblich geringere Fehler zu komplexen numerischen Modellen oder den theoretischen Werten (bei Näherungsformeln) mit angegeben.
Ausgabegröße
Fehler bzgl. Theorie
Fehler bzgl. Beobachtung
Skalierungsfaktoren
(exakt)
unter 1 %
Überdruck Freiluft
(gering)
±15 %–±30 %
Überdruck mit Reflexion
±4 % (max. 11 %)
±30 %
Laufzeit
ca. 1 %
±15 %
Die wahrscheinliche Explosion eines Meteoriden beim Tunguska-Ereignis lässt sich näherungsweise durch eine Explosion von etwa 15 MT TNT-Äquivalent in ca. 8 km Höhe darstellen. Für solch eine Explosion liefert obiges Modell einen Überdruck von 101 kPa (knapp 1 atm ) im Hypozentrum, 35 kPa im Umkreis von 16 km (hier treten schwerste Verwüstungen auf, was sich mit den Beobachtungen deckt). Orkanartige Winde über 11 Bft treten im Umkreis von 30 km auf und lassen noch einzelne Bäume umstürzen. In 65 km Grundradius beträgt der Druck noch mehr als 4 kPa, wodurch Fenster und Türen eingedruckt und Dächer beschädigt werden. Der Windstoß im Freien beträgt in diesem Abstand nicht mehr als 10 m/s (5 Bft), jedoch kann an Öffnungen (Türen, Fenster) der Überdruck zu kurzzeitigen Strömungen von bis zu 69 m/s führen und Personen umwerfen. Dies deckt sich mit beobachteten Schäden und Zeugenaussagen in der Stadt Wanawara, die 65 km vom vermuteten Hypozentrum entfernt liegt. Dort traf die Druckwelle dem DNA-Modell zufolge nach knapp drei Minuten ein (175 sek Fit, 176 sek integriert; Standardatmosphäre 1976 ).
Feuerballentwicklung bei Kernexplosionen
Bearbeiten
Feuerballtemperatur (oben) und -durchmesser (unten) einer 20-kT-Luftexplosion als Funktion der Zeit. Die orange Teilkurve zeigt die durch Absorption scheinbar reduzierte Effektivtemperatur im Frühstadium. Eng mit der Druckwellenausbreitung hängt auch die Ausbildung des Feuerballs einer Kernwaffenexplosion zusammen. Im Wesentlichen gibt es drei Hauptphasen, die im genannten Artikel beschrieben werden:
Ausdehnung durch Strahlungstransport (<10-4 Sekunden bei 20 Kilotonnen),
Ausdehnung als glühende Stoßfront (<10-2 Sekunden),
Nachglühen der heißen Gase (<10 Sekunden). In dichten Atmosphärenschichten (unter 30 Kilometer Höhe) ist die Dauer und die räumliche Ausdehnung der ersten Phase gegenüber den nachfolgenden Phasen vernachlässigbar. Die folgenden können daher annähernd unabhängig von der ersten beschrieben werden. Die folgenden Formeln sind gültig für Höhen unter 30 km, wo die mittlere freie Weglänge für die primären Röntgenstrahlen klein gegenüber dem skalierten Feuerballdurchmesser sind und ein Feuerball somit auf ähnliche Weise entstehen kann, wie auf Meeresniveau. Generell sind diese Formeln nur Näherungen, die mit entsprechender Vorsicht zu verwenden sind.
Das Wachstum des Feuerballs in der 2. Phase skaliert mit der Explosionsenergie in der gleichen Weise wie die Druckwelle selbst (Bezeichnungen siehe oben ):
S
L
=
S
P
−
1
/
3
;
S
D
=
S
L
S
T
{\displaystyle S_{L}=S_{P}^{-1/3}\ ;\qquad S_{D}={\frac {S_{L}}{\sqrt {S_{T}}}}}
Um die mit Umgebungsbedingungen und Sprengkraft sowie Sprengkopftyp (geringfügig) unterschiedlichen Energieanteile von Druckwelle ξb und Wärme ξh (letztere ist für die Ausdehnung des späten Feuerballs maßgeblich) zu berücksichtigen, werden mechanische („blast“) und thermische („heat“) Sprengkraft, W b und W h unterschieden:
W
b
=
W
ξ
b
0
,
50
,
W
h
=
W
ξ
h
0
,
35
{\displaystyle W_{\mathrm {b} }=W{\frac {\xi _{\mathrm {b} }}{0{,}50}}\ ,\quad W_{\mathrm {h} }=W{\frac {\xi _{\mathrm {h} }}{0{,}35}}}
Bei einer Explosion im Kilotonnenbereich sind die Anteile etwa ξh = 50 % und ξh = 35 % und somit W b = W h = W .
Aus in der Literatur vorhandenen Diagrammen ist folgende Näherungsformel für eine 20-kT-Luftexplosion gewonnen worden, die die Grundlage für die obige Abbildung ist (man beachte, dass dort der Durchmesser D = 2R angegeben ist):
R
(
t
)
=
[
(
R
−
4
t
C
)
−
3
+
R
∞
−
3
]
−
1
/
3
;
R
−
4
=
13
m
;
R
∞
=
236
m
;
C
=
0,406
.
{\displaystyle R(t)=\left[\left(R_{-4}t^{C}\right)^{-3}+R_{\infty }^{-3}\right]^{-1/3}\ ;\quad R_{-4}=13\,\mathrm {m} \ ;\ R_{\infty }=236\,\mathrm {m} \ ;\ C=0{,}406\ .}
t ist dabei der Betrag der Zeit nach der Zündung in Sekunden und wird als dimensionslose Zahl verwendet. Der späte Feuerballdurchmesser (3. Phase) R ∞ skaliert mit W 0,39 statt mit der Kubikwurzel, so dass sich für die W -Skalierung ergibt:
R
(
t
,
W
)
=
[
(
S
0
W
b
(
1
−
C
)
/
3
R
0
t
C
)
−
3
+
(
S
∞
W
h
0
,
39
R
∞
)
−
3
]
−
1
/
3
,
{\displaystyle R(t,W)=\left[\left(S_{0}W_{\mathrm {b} }^{(1-C)/3}R_{0}t^{C}\right)^{-3}+\left(S_{\infty }W_{\mathrm {h} }^{0{,}39}R_{\infty }\right)^{-3}\right]^{-1/3}\ ,}
R
0
=
303
m
,
R
∞
=
73
m
.
{\displaystyle R_{0}=303\,\mathrm {m} \ ,\quad R_{\infty }=73\,\mathrm {m} \ .}
Dabei W wieder in Einheiten von kT TNT-Äquivalent, ferner ist R 0 ein auf 1 Sekunde nach dem t C R ∞ , sowie S 0 und S ∞ Skalierungsfaktoren für Umgebungsdruck und -temperatur (auf oder nahe Meeresniveau können sie auf 1 gesetzt werden). S 0 ist einfach zu berechnen, da nur die Längen- und Zeit-Skalierungsfaktoren für die Druckwelle (auch für das Zeitargument t ) eingehen:
S
0
=
S
P
C
−
1
3
S
T
C
/
2
{\displaystyle S_{0}=S_{P}^{\frac {C-1}{3}}S_{T}^{C/2}}
S ∞ ist weniger offensichtlich, da auch die optische Dicke τ eine wichtige Rolle spielt. Eine erste Näherung berücksichtigt nur die Zunahme des Radius mit abnehmendem Druck:
S
∞
≈
S
P
−
1
/
3
{\displaystyle S_{\infty }\approx S_{P}^{-1/3}}
Die effektive optische Dicke, die für den gegenüber 1/3 etwas größeren Exponenten von W verantwortlich ist, nimmt jedoch mit abnehmendem Druck (geringere Luftdichte) sowie der damit zunehmenden Ausdehnungszeit (Feuerball hat mehr Zeit zum Abstrahlen) ab. Mit der Beziehung
R
(
W
h
)
=
R
(
1
k
T
)
τ
0
,
17
{\displaystyle R(W_{\mathrm {h} })=R(1kT)\tau ^{0{,}17}}
der relativen Dichte S ρ =ρ/ρ0 und
τ
≈
W
h
1
/
3
S
ρ
2
/
3
⋅
S
D
−
1
=
W
h
1
/
3
(
S
P
S
T
)
2
/
3
⋅
S
P
1
/
3
S
T
1
/
2
=
W
h
1
/
3
S
P
⋅
S
K
−
1
/
6
{\displaystyle \tau \approx W_{\mathrm {h} }^{1/3}S_{\rho }^{2/3}\cdot S_{D}^{-1}=W_{\mathrm {h} }^{1/3}\left({\frac {S_{P}}{S_{T}}}\right)^{2/3}\cdot S_{P}^{1/3}S_{T}^{1/2}=W_{\mathrm {h} }^{1/3}S_{P}\cdot S_{K}^{-1/6}}
ergibt sich
S
∞
≈
W
h
0
,
39
S
P
−
0,163
33
…
S
T
−
0,028
333
…
.
{\displaystyle S_{\infty }\approx W_{\mathrm {h} }^{0{,}39}S_{P}^{-0{,}16333\dots }S_{T}^{-0{,}028333\dots }\ .}
Die Temperatur hat demnach nur geringen Einfluss auf den Endradius. Eine vernünftige Näherung ist somit
R
(
t
,
W
)
=
[
(
[
W
b
S
P
]
0,198
S
T
0,203
R
0
t
0,406
)
−
3
+
(
W
h
0
,
39
S
P
−
0
,
2
R
∞
)
−
3
]
−
1
/
3
.
{\displaystyle R(t,W)=\left[\left(\left[{\frac {W_{\mathrm {b} }}{S_{P}}}\right]^{0{,}198}S_{T}^{0{,}203}R_{0}t^{0{,}406}\right)^{-3}+\left(W_{\mathrm {h} }^{0{,}39}S_{P}^{-0{,}2}R_{\infty }\right)^{-3}\right]^{-1/3}\ .}
Im Fall von Bodenexplosionen ist nur W b aufgrund von Reflexion zu verdoppeln; wegen der Absorption von ungefähr der Hälfte der Wärme am Boden kann für W h am Boden der gleiche Wert wie für Luftexplosionen eingesetzt werden.
Für die theoretische Effektivtemperatur (d. h. die einem Planck-Strahler gleicher Strahlkraft entsprechende Temperatur) T the des Feuerballs einer 20-kT-Explosion wurde aus Abb. 2.123 aus EoNW77 eine zusammengesetzte Näherungsfunktion gewonnen:
log
10
(
T
t
h
e
)
=
{
g
1
(
τ
)
wenn
τ
≤
−
2,507
g
2
(
τ
)
wenn
τ
≤
−
0,686
g
3
(
τ
)
sonst
{\displaystyle \log _{10}(T_{\mathrm {the} })={\begin{cases}g_{1}(\tau )&{\mbox{wenn }}\tau \leq -2{,}507\\g_{2}(\tau )&{\mbox{wenn }}\tau \leq -0{,}686\\g_{3}(\tau )&{\mbox{sonst}}\end{cases}}}
wobei τ = log10 t und
g
1
(
τ
)
=
−
1,103
046
τ
+
1,032
988
g
2
(
τ
)
=
p
6
τ
6
+
p
5
τ
5
+
p
4
τ
4
+
p
3
τ
3
+
p
2
τ
2
+
p
1
τ
+
p
0
g
3
(
τ
)
=
−
0,547
586
τ
+
3,505
928
{\displaystyle {\begin{matrix}g1(\tau )&=&-1{,}103046\,\tau +1{,}032988\\g2(\tau )&=&p_{6}\,\tau ^{6}+p_{5}\,\tau ^{5}+p_{4}\,\tau ^{4}+p_{3}\,\tau ^{3}+p_{2}\,\tau ^{2}+p_{1}\,\tau +p_{0}\\g3(\tau )&=&-0{,}547586\,\tau +3{,}505928\end{matrix}}}
Die gemessene Effektivtemperatur T obs in der Frühphase ist deutlich geringer, was auf Absorption durch ionisierte Luftgase zurückgeführt werden kann. In diesem Fall wird
log
10
(
T
o
b
s
)
=
{
h
(
τ
)
wenn
τ
≤
−
2,226
38
g
2
(
τ
)
wenn
τ
≤
−
0,686
g
3
(
τ
)
sonst
{\displaystyle \log _{10}(T_{\mathrm {obs} })={\begin{cases}h(\tau )&{\mbox{wenn }}\tau \leq -2{,}22638\\g_{2}(\tau )&{\mbox{wenn }}\tau \leq -0{,}686\\g_{3}(\tau )&{\mbox{sonst}}\end{cases}}}
mit
h
(
τ
)
=
q
5
τ
5
+
q
4
τ
4
+
q
3
τ
3
+
q
2
τ
2
+
q
1
τ
+
q
0
{\displaystyle h(\tau )=q_{5}\,\tau ^{5}+q_{4}\,\tau ^{4}+q_{3}\,\tau ^{3}+q_{2}\,\tau ^{2}+q_{1}\,\tau +q_{0}}
Die Koeffizienten sind
p
0
=
2
,
8526650801
q
0
=
69
,
18513566
{\displaystyle p_{0}=2,8526650801\quad q_{0}=69,18513566}
p
1
=
−
1
,
0863702704
q
1
=
115
,
00394909
{\displaystyle p_{1}=-1,0863702704\quad q_{1}=115,00394909}
p
2
=
4
,
7729619842
q
2
=
79
,
77893973
{\displaystyle p_{2}=4,7729619842\quad q_{2}=79,77893973}
p
3
=
10
,
026967289
q
3
=
27
,
50798341
{\displaystyle p_{3}=10,026967289\quad q_{3}=27,50798341}
p
4
=
7
,
1862268373
q
4
=
4
,
74096116
{\displaystyle p_{4}=7,1862268373\quad q_{4}=4,74096116}
p
5
=
2
,
2724484357
q
5
=
0
,
32749001
{\displaystyle p_{5}=2,2724484357\quad q_{5}=0,32749001}
p
6
=
0
,
27143255706
{\displaystyle p_{6}=0,27143255706\ }
Die Leuchtkraft ergibt sich dann aus dem Stefan-Boltzmann-Gesetz :
4
π
R
2
σ
T
e
f
f
4
{\displaystyle 4\pi R^{2}\sigma T_{\mathrm {eff} }^{4}\,}
wobei σ = 5.6704·10-8 W m-2 K-4 die Stefan-Boltzmann-Konstante ist.
Nach Beobachtungen wird etwa 1 % der thermischen Energie im ersten „Peak“ freigesetzt. Dieses entspricht jedoch einer Temperaturfunktion, die zwischen beiden obigen Funktionen liegt. Ein sinnvoller Kompromiss ist offenbar
log
10
(
T
e
f
f
)
=
0
,
4
⋅
log
10
(
T
o
b
s
)
+
0
,
6
⋅
log
10
(
T
t
h
e
)
{\displaystyle \log _{10}(T_{\mathrm {eff} })=0{,}4\cdot \log _{10}(T_{\mathrm {obs} })+0{,}6\cdot \log _{10}(T_{\mathrm {the} })\,}
Ferner deuten andere Daten auf einen geringfügig (ca. 20 %) langsameren Verlauf der Explosion im zweiten Peak hin, was durch die Korrektur
T
e
f
f
′
=
0.77
⋅
10
f
k
o
r
r
⋅
T
e
f
f
;
{\displaystyle T_{\mathrm {eff} }'=0.77\cdot 10^{f_{\mathrm {korr} }}\cdot T_{\mathrm {eff} }\ ;}
f
k
o
r
r
=
{
0.0821379
⋅
(
τ
+
0.75
)
wenn
τ
>
−
0
,
75
0
sonst
{\displaystyle f_{\mathrm {korr} }={\begin{cases}0.0821379\cdot (\tau +0.75)&{\mbox{wenn }}\tau >-0{,}75\\0&{\mbox{sonst}}\end{cases}}}
unter Erhaltung der abgestrahlten Energie erreicht wird. Ursache für diese Diskrepanz sind vermutlich Ungenauigkeiten in den publizierten Daten. Für die Abbildung wurde die unkorrigierte (und damit der Originalabbildung am ehesten entsprechende) Funktion verwendet.
Die zeitliche Entwicklung der Helligkeit zu Beginn des zweiten thermischen Impulses skaliert anders als die räumliche Ausdehnung. Nach EoNW77 ist die zeitliche Skalierung gegeben durch
S
D
,
l
u
m
≈
W
0
,
44
⋅
S
ρ
0
,
36
.
{\displaystyle S_{D,\mathrm {lum} }\approx W^{0{,}44}\cdot S_{\rho }^{0{,}36}\ .}
Die Leuchtkraft (Strahlleistung) L skaliert mit
S
D
,
l
u
m
≈
W
0
,
59
⋅
S
ρ
−
0
,
45
.
{\displaystyle S_{D,\mathrm {lum} }\approx W^{0{,}59}\cdot S_{\rho }^{-0{,}45}\ .}
Der Feuerball wird also heller mit zunehmender Höhe (also abnehmender Luftdichte), leuchtet dafür aber kürzer.
Aus den Skalierungsregeln der Druckwelle für Explosionsenergie und Umgebungsdruck sowie denen aus EoNW77 für die Zeitentwicklung der Leuchtkraft lässt sich ein Ähnlichkeitsparameter f ableiten, indem beide Skalierungsregeln gleichgesetzt werden:
W
0
,
44
⋅
S
P
0
,
36
⋅
S
T
−
0
,
36
=
W
1
/
3
⋅
S
P
1
/
3
{\displaystyle W^{0{,}44}\cdot S_{P}^{0{,}36}\cdot S_{T}^{-0{,}36}=W^{1/3}\cdot S_{P}^{1/3}}
⇒
f
=
W
⋅
S
P
13
/
2
⋅
S
T
−
27
/
8
=
W
⋅
S
P
6
,
5
⋅
S
T
−
3,375
{\displaystyle \Rightarrow f=W\cdot S_{P}^{13/2}\cdot S_{T}^{-27/8}=W\cdot S_{P}^{6{,}5}\cdot S_{T}^{-3{,}375}}
Für den ungefähren Bereich 1 ≤ f ≤ 20000 gilt dann für Zeit- und Längenskalierung
S
D
=
W
S
P
1
/
3
⋅
f
8
/
75
;
S
L
=
W
S
P
1
/
3
⋅
f
17
/
300
.
{\displaystyle S_{D}={W \over S_{P}}^{1/3}\cdot f^{8/75}\ ;\quad S_{L}={W \over S_{P}}^{1/3}\cdot f^{17/300}\ .}
Für sehr kleine f <1 nimmt die thermische Emissionszeit weiter ab, während der Enddurchmesser zunehmend von der Druckwelle bestimmt wird und daher mit (Y /S P 1/3 oder geringfügig flacher skaliert (siehe Unterabschnitt zum Feuerballwachstum für eine Kompromisslösung). Bei sehr großen f >20000 geht die optische Dicke der die Feuerblase verhüllenden Stoßfront gegen unendlich und verschwindet erst unterhalb einer bestimmten Temperatur, dann jedoch schlagartig. Größere Feuerballdurchmesser ändern daran nichts mehr, so dass auch hier eine (Y /S P 1/3 -Skalierung, jedoch für Radius und Leuchtdauer zu erwarten ist. Für diese Bereiche liegen jedoch keine Messwerte vor, so dass dies nur grobe Schätzungen sind. Ferner ist die f -Charakterisierung nur gültig, solange die mittlere freie Weglänge der direkten Röntgenstrahlung aus dem Explosionszentrum klein gegenüber dem Feuerballdurchmesser ist (das ist oberhalb von etwa 30 km nicht mehr gegeben), sowie der Feuerballradius kleiner als die Skalenhöhe der Atmosphäre ist. Bei Umrechnungen auf die Atmosphäre eines anderen Planeten (z. B. zur Modellierung des Shoemaker-Levy 9 -Einschlags auf Jupiter ) ist zudem deren unterschiedliche Zusammensetzung zu berücksichtigen.
Feuerbälle mit f =1 können mit der abgebildeten Zeit-Temperatur-Kurve berechnet werden, wobei die Zeit und der Durchmesser mit (Y /S P 1/3 und die Temperatur mit S P 1/4 skaliert wird. Letzteres bedeutet anschaulich: Bei 1/8 des Meerenhöhendrucks dehnt sich der skalengleiche Feuerball doppelt so weit aus wie in Meereshöhe bei simpler Kubikwurzelskalierung bei gleicher Energie, und er braucht dafür doppelt so lange. Die Energie wird daher über die vierfache Fläche halb so schnell freigesetzt, also mit 1/8 der Intensität. Die Intensität skaliert bei konstantem f also linear mit dem Druck. Aus dem Stefan-Boltzmann-Gesetz folgt dann die Skalierung der Temperatur.
Die Entwicklung der Pilzwolke hängt stark von den Wetterbedingungen ab. Dennoch ist es möglich, für durchschnittliche Bedingungen und annähernd Windstille eine Näherung zu beschreiben. Für kleine W h (bis ca. 10 kT) gilt für Endhöhe H und -breite B der Pilzwolke
H
≈
3000
m
⋅
W
h
1
/
3
;
B
≈
1200
m
⋅
W
h
1
/
3
.
{\displaystyle H\approx 3000\,\mathrm {m} \cdot W_{\mathrm {h} }^{1/3}\ ;\quad B\approx 1200\,\mathrm {m} \cdot W_{\mathrm {h} }^{1/3}\ .}
Für größere Energien wird die Form der Wolke stark von der atmosphärischen Schichtung (v.a. der Tropopause ) beeinflusst. Der Aufstieg wird gehemmt, während die Wolke sich stärker in die Breite ausdehnt. Die folgende Formel ist eine Anpassung an die Abbildung 2.16 aus EoNW77.
H
(
W
)
=
3000
m
⋅
10
0,006
941
L
W
4
−
0,062
16
L
W
3
+
0,152
6
L
W
2
+
0,187
8
L
W
{\displaystyle H(W)=3000\,\mathrm {m} \cdot 10^{0{,}006941{\mathit {LW}}^{4}-0{,}06216{\mathit {LW}}^{3}+0{,}1526{\mathit {LW}}^{2}+0{,}1878{\mathit {LW}}}}
R
(
W
)
=
1200
m
⋅
10
0,013
7
L
W
3
−
0,035
8
L
W
2
+
0
,
37
L
W
{\displaystyle R(W)=1200\,\mathrm {m} \cdot 10^{0{,}0137{\mathit {LW}}^{3}-0{,}0358{\mathit {LW}}^{2}+0{,}37{\mathit {LW}}}}
wobei LW = log10 (W /kT). Der stetige Übergang beider Näherungen wird durch eine Interpolation unterhalb von etwa LW = 1.5 bzw. W h = 30 kT ermöglicht.
Die Zeit bis zum Erreichen der Endhöhe kann für W h < 1 MT grob abgeschätzt werden durch die Beziehung
t
e
n
d
≈
60
s
⋅
W
0.25
,
{\displaystyle t_{\mathrm {end} }\approx 60\,\mathrm {s} \cdot W^{0.25}\ ,}
die Steigrate durch
v
r
i
s
e
≈
75
m
s
−
1
⋅
W
0.06
.
{\displaystyle v_{\mathrm {rise} }\approx 75\,\mathrm {m\,s^{-1}} \cdot W^{0.06}\ .}
(Quelle: Daten aus EoNW64, PDF bei Trinity Atomic Web Site als Grundlage für Potenzgesetz-Abschätzung.)
U
=
T
S
−
P
V
{\displaystyle U=TS-PV\,}
H
=
U
+
P
V
{\displaystyle H=U+PV\,}
G
=
H
−
T
S
{\displaystyle G=H-TS\,}
F
=
U
−
T
S
{\displaystyle F=U-TS\,}
d
U
=
T
d
S
−
P
d
V
+
∑
i
=
1
k
μ
i
d
n
i
{\displaystyle dU=TdS-PdV+\sum _{i=1}^{k}\mu _{i}dn_{i}}
d
H
=
T
d
S
+
V
d
P
+
∑
i
=
1
k
μ
i
d
n
i
{\displaystyle dH=TdS+VdP+\sum _{i=1}^{k}\mu _{i}dn_{i}}
d
G
=
−
S
d
T
+
V
d
P
+
∑
i
=
1
k
μ
i
d
n
i
{\displaystyle dG=-SdT+VdP+\sum _{i=1}^{k}\mu _{i}dn_{i}}
d
F
=
−
S
d
T
−
P
d
V
+
∑
i
=
1
k
μ
i
d
n
i
{\displaystyle dF=-SdT-PdV+\sum _{i=1}^{k}\mu _{i}dn_{i}}
C
V
=
(
∂
U
∂
T
)
V
{\displaystyle C_{V}=\left({\frac {\partial U}{\partial T}}\right)_{V}}
C
P
=
(
∂
H
∂
T
)
P
{\displaystyle C_{P}=\left({\frac {\partial H}{\partial T}}\right)_{P}}
−
(
∂
P
∂
S
)
V
=
(
∂
T
∂
V
)
S
{\displaystyle -\left({\frac {\partial P}{\partial S}}\right)_{V}=\left({\frac {\partial T}{\partial V}}\right)_{S}}
(
∂
V
∂
S
)
P
=
(
∂
T
∂
P
)
S
{\displaystyle \left({\frac {\partial V}{\partial S}}\right)_{P}=\left({\frac {\partial T}{\partial P}}\right)_{S}}
(
∂
V
∂
T
)
P
=
−
(
∂
S
∂
P
)
T
{\displaystyle \left({\frac {\partial V}{\partial T}}\right)_{P}=-\left({\frac {\partial S}{\partial P}}\right)_{T}}
(
∂
S
∂
V
)
T
=
(
∂
P
∂
T
)
V
{\displaystyle \left({\frac {\partial S}{\partial V}}\right)_{T}=\left({\frac {\partial P}{\partial T}}\right)_{V}}
Freie Enthalpie:
0
=
S
d
T
−
V
d
P
+
∑
i
=
1
k
n
i
d
μ
i
{\displaystyle 0=SdT-VdP+\sum _{i=1}^{k}n_{i}d\mu _{i}}
S= maximum
G= minimum
Freiheitsgrade
=
Komponenten
+
2
−
Phasen
{\displaystyle {\text{Freiheitsgrade}}={\text{Komponenten}}+2-{\text{Phasen}}\,}
d
P
L
V
d
T
=
Δ
S
L
V
Δ
V
L
V
=
Δ
H
L
V
T
Δ
V
L
V
{\displaystyle {\frac {dP^{LV}}{dT}}={\frac {\Delta S^{LV}}{\Delta V^{LV}}}={\frac {\Delta H^{LV}}{T\Delta V^{LV}}}}
ln
P
L
V
=
A
−
B
T
{\displaystyle \ln P^{LV}=A-{\frac {B}{T}}}
ln
P
L
V
=
A
−
B
T
+
C
{\displaystyle \ln P^{LV}=A-{\frac {B}{T+C}}}
(
∂
G
T
∂
T
)
=
−
H
T
2
{\displaystyle \left({\frac {\partial {\frac {G}{T}}}{\partial T}}\right)=-{\frac {H}{T^{2}}}}
Definition:
φ
0
,
i
=
f
0
,
i
(
T
,
P
)
P
{\displaystyle \varphi _{0,i}={\frac {f_{0,i}(T,P)}{P}}}
lim
P
→
∞
f
0
,
i
(
T
,
P
)
=
P
{\displaystyle \lim _{P\to \infty }f_{0,i}(T,P)=P}
lim
P
→
∞
φ
0
,
i
(
T
,
P
)
=
1
{\displaystyle \lim _{P\to \infty }\varphi _{0,i}(T,P)=1}
Reine Komponenten:
ln
φ
0
,
i
(
T
,
P
)
=
∫
0
P
z
−
1
P
d
P
{\displaystyle \ln \varphi _{0,i}(T,P)=\int _{0}^{P}{\frac {z-1}{P}}dP}
ln
φ
0
,
i
(
T
,
P
)
=
z
−
1
−
ln
z
+
∫
V
∞
z
−
1
V
d
V
{\displaystyle \ln \varphi _{0,i}(T,P)=z-1-\ln z+\int _{V}^{\infty }{\frac {z-1}{V}}dV}
Mischungen:
ln
φ
i
(
T
,
P
)
=
∫
0
P
(
v
i
R
T
−
1
P
)
d
P
{\displaystyle \ln \varphi _{i}(T,P)=\int _{0}^{P}\left({\frac {v_{i}}{RT}}-{\frac {1}{P}}\right)dP}
ln
φ
i
(
T
,
P
)
=
∫
V
∞
(
−
1
R
T
(
∂
P
∂
n
i
)
T
,
V
,
n
≠
j
+
1
V
)
d
V
−
ln
z
{\displaystyle \ln \varphi _{i}(T,P)=\int _{V}^{\infty }\left(-{\frac {1}{RT}}\left({\frac {\partial P}{\partial n_{i}}}\right)_{T,V,{n\neq j}}+{\frac {1}{V}}\right)dV-\ln z}
Leidenform:
z
=
P
v
R
T
=
1
+
B
(
T
)
ρ
+
C
(
T
)
ρ
2
+
.
.
.
=
1
+
B
(
T
)
v
+
C
(
T
)
v
2
+
.
.
.
{\displaystyle z={\frac {Pv}{RT}}=1+B(T)\rho +C(T)\rho ^{2}+...=1+{\frac {B(T)}{v}}+{\frac {C(T)}{v^{2}}}+...}
Berlinform:
z
=
P
v
R
T
=
1
+
B
′
(
T
)
P
+
C
′
(
T
)
P
2
+
.
.
.
{\displaystyle z={\frac {Pv}{RT}}=1+B'(T)P+C'(T)P^{2}+...}
Umrechnungsformel:
B
′
≈
B
R
T
{\displaystyle B'\approx {\frac {B}{RT}}}
C
′
≈
C
−
B
2
(
R
0
T
)
2
{\displaystyle C'\approx {\frac {C-B^{2}}{{(R_{0}T)}^{2}}}}
Bei Boyle-Temperatur ist das PVT-Verhalten ideal.
B
(
T
B
)
=
0
{\displaystyle B(T^{B})=0\,}
Allgemein:
(
P
+
a
v
2
)
(
v
−
b
)
=
R
T
{\displaystyle \left(P+{\frac {a}{v^{2}}}\right)\left(v-b\right)=RT}
nach Druck P:
P
=
R
T
v
−
b
−
a
v
2
{\displaystyle P={\frac {RT}{v-b}}-{\frac {a}{v^{2}}}}
nach z:
z
=
P
v
R
T
=
v
v
−
b
−
a
v
R
T
{\displaystyle z={\frac {Pv}{RT}}={\frac {v}{v-b}}-{\frac {a}{vRT}}}
Generalisierten Form:
[
P
P
k
r
+
3
(
v
k
r
v
)
2
]
[
3
v
v
k
r
−
1
]
=
8
T
T
k
r
{\displaystyle \left[{\frac {P}{P_{kr}}}+3\left({\frac {v_{kr}}{v}}\right)^{2}\right]\left[3{\frac {v}{v_{kr}}}-1\right]=8{\frac {T}{T_{kr}}}}
v
k
r
=
3
b
{\displaystyle v_{kr}=3b\,}
T
k
r
=
8
a
27
b
R
{\displaystyle T_{kr}={\frac {8a}{27bR}}}
P
k
r
=
a
27
b
2
{\displaystyle P_{kr}={\frac {a}{27b^{2}}}}
Reduzierte Form:
(
P
r
+
3
v
r
2
)
(
3
v
r
−
1
)
=
8
T
r
{\displaystyle \left(P_{r}+{\frac {3}{v_{r}^{2}}}\right)\left(3v_{r}-1\right)=8T_{r}}
v
r
=
v
v
k
r
{\displaystyle v_{r}={\frac {v}{v_{kr}}}}
T
r
=
T
T
k
r
{\displaystyle T_{r}={\frac {T}{T_{kr}}}}
P
r
=
P
P
k
r
{\displaystyle P_{r}={\frac {P}{P_{kr}}}}
B
(
T
)
=
b
−
a
R
T
{\displaystyle B(T)=b-{\frac {a}{RT}}}
T
B
=
a
R
b
{\displaystyle T^{B}={\frac {a}{Rb}}}
Zweiparameterkorrespondenzprinzip:
Stoffe sind vergleichbar, wenn sie aus vergleichbaren Punkten betrachtet werden. Dreiparameterkorrespondenzprinzip:
z
=
z
0
+
ω
0
,
i
z
1
{\displaystyle z=z_{0}+\omega _{0,i}z_{1}\,}
mit Pitzerfaktor
ω
0
,
i
=
−
1
−
log
(
P
0
,
i
L
V
(
T
r
=
0
,
7
)
P
k
r
)
{\displaystyle \omega _{0,i}=-1-\log \left({\frac {P_{0,i}^{LV}(T_{r}=0,7)}{P_{kr}}}\right)}
o
i
¯
=
(
∂
O
∂
n
i
)
T
,
P
,
n
i
≠
j
{\displaystyle {\overline {o_{i}}}=\left({\frac {\partial O}{\partial n_{i}}}\right)_{T,P,n_{i\neq j}}}
1. Differenzansatz:
Δ
o
=
o
i
d
e
a
l
−
o
r
e
a
l
{\displaystyle \Delta o=o_{ideal}-o_{real}\,}
2. Partielle molare Ansatz:
o
=
∑
i
=
1
k
o
¯
i
x
i
{\displaystyle o=\sum _{i=1}^{k}{\overline {o}}_{i}x_{i}}
O
=
∑
i
=
1
k
o
¯
i
n
i
{\displaystyle O=\sum _{i=1}^{k}{\overline {o}}_{i}n_{i}}
3. Exzessansatz:
o
=
∑
i
=
1
k
x
i
o
i
+
Δ
o
i
d
e
a
l
+
o
E
{\displaystyle o=\sum _{i=1}^{k}x_{i}o_{i}+\Delta o^{ideal}+o^{E}}
Definition:
γ
i
=
φ
i
L
φ
0
,
i
L
{\displaystyle \gamma _{i}={\frac {\varphi _{i}^{L}}{\varphi _{0,i}^{L}}}}
Allgemein:
Isofugazitätskriterium
f
i
V
=
f
i
L
{\displaystyle f_{i}^{V}=f_{i}^{L}}
f
i
V
=
y
i
φ
i
P
{\displaystyle f_{i}^{V}=y_{i}\varphi _{i}P}
f
i
L
=
x
i
γ
i
f
0
,
i
L
=
x
i
γ
i
P
0
,
i
L
V
φ
0
,
i
L
V
Π
{\displaystyle f_{i}^{L}=x_{i}\gamma _{i}f_{0,i}^{L}=x_{i}\gamma _{i}P_{0,i}^{LV}\varphi _{0,i}^{LV}\Pi }
Poynting-Korrektur
Π
=
exp
(
∫
P
0
,
i
L
V
P
v
0
,
i
L
R
T
d
P
)
{\displaystyle \Pi =\exp \left(\int _{P_{0,i}^{LV}}^{P}{\frac {v_{0,i}^{L}}{RT}}dP\right)}
Vereinfacht:
x
i
γ
i
P
0
,
i
L
V
=
y
i
P
{\displaystyle x_{i}\gamma _{i}P_{0,i}^{LV}=y_{i}P}
Raoultsche Gesetz:
x
i
P
0
,
i
L
V
=
y
i
P
{\displaystyle x_{i}P_{0,i}^{LV}=y_{i}P}
∑
i
=
1
k
(
f
exp
,
i
−
f
cal
,
i
)
2
=
!
minimal
{\displaystyle \sum _{i=1}^{k}\left(f_{{\text{exp}},i}-f_{{\text{cal}},i}\right)^{2}{\stackrel {!}{=}}{\text{minimal}}}
Dieses Kapitel erläutert die physikalische Bedeutung des Strahlungsgesetzes. Für die hier behandelte mathematische Darstellung des Gesetzes existieren zahlreiche verschiedene Varianten, je nachdem ob das Gesetz in Abhängigkeit von der Frequenz oder der Wellenlänge formuliert werden soll, ob die Intensität der Strahlung in eine bestimmte Richtung oder die Abstrahlung in den gesamten Halbraum betrachtet werden soll, ob Strahlgrößen, Energiedichten oder Photonenzahlen beschrieben werden sollen. Diese verschiedenen Formen werden im Folgenden in ihrem gegenseitigen Zusammenhang dargestellt und erläutert. Die Formelsammlung enthält auch unmittelbar aus dem planckschen Strahlungsgesetz abgeleitete Gesetze wie z. B. das Stefan-Boltzmann-Gesetz .
Wie bei radiometrischen Größen üblich, können auch zur Beschreibung des Spektrums eines Schwarzen Körpers verschiedene Strahlungsgrößen verwendet werden. Die hier benutzten Bezeichnungen und Symbole folgen der DIN EN ISO 9288 (August 1996). Der obere Index
o
{\displaystyle \,^{o}}
Brechzahl
n
{\displaystyle n}
c
{\displaystyle c}
c
/
n
{\displaystyle c/n}
λ
{\displaystyle \lambda }
λ
/
n
{\displaystyle \lambda /n}
ν
{\displaystyle \nu }
[ 1]
Man unterscheidet
spektrale Größen, welche die Frequenz- bzw. Wellenlängenabhängigkeiten explizit beschreibenGesamt größen, welche über alle Frequenzen bzw. Wellenlängen integriert sindsowie
gerichtete Größen, welche die Richtungsabhängigkeiten explizit beschreibenhemisphärische Größen, welche über alle Richtungen des Halbraums integriert sind.Die spektrale Strahldichte
L
Ω
ν
(
β
,
φ
,
ν
,
T
)
{\displaystyle \,L_{\Omega \nu }(\beta ,\varphi ,\nu ,T)}
Für die spektrale Strahldichte
L
Ω
ν
o
{\displaystyle L_{\Omega \nu }^{o}}
Schwarzen Körpers der absoluten Temperatur T gilt
in der Frequenzdarstellung:
L
Ω
ν
o
(
ν
,
T
)
cos
(
β
)
d
A
d
ν
d
Ω
=
2
h
ν
3
c
2
1
e
(
h
ν
k
T
)
−
1
cos
(
β
)
d
A
d
ν
d
Ω
{\displaystyle L_{\Omega \nu }^{o}(\nu ,T)\,\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \nu \,\mathrm {d} \Omega ={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}\cos(\beta )\mathrm {d} A\,\mathrm {d} \nu \,\mathrm {d} \Omega }
SI-Einheit von
L
Ω
ν
o
(
ν
,
T
)
{\displaystyle L_{\Omega \nu }^{o}(\nu ,T)}
-2 Hz-1 sr-1 ,
in der Wellenlängendarstellung:
L
Ω
λ
o
(
λ
,
T
)
cos
(
β
)
d
A
d
λ
d
Ω
=
2
h
c
2
λ
5
1
e
(
h
c
λ
k
T
)
−
1
cos
(
β
)
d
A
d
λ
d
Ω
{\displaystyle L_{\Omega \lambda }^{o}(\lambda ,T)\,\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \lambda \,\mathrm {d} \Omega ={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}\cos(\beta )\mathrm {d} A\,\mathrm {d} \lambda \,\mathrm {d} \Omega }
SI-Einheit von
L
Ω
λ
o
(
λ
,
T
)
{\displaystyle L_{\Omega \lambda }^{o}(\lambda ,T)}
-2 μm-1 sr-1 .
L
Ω
ν
o
(
ν
,
T
)
cos
(
β
)
d
A
d
ν
d
Ω
{\displaystyle L_{\Omega \nu }^{o}(\nu ,T)\,\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \nu \,\mathrm {d} \Omega }
A im Frequenzbereich zwischen ν und ν + dν in das zwischen den Azimutwinkeln φ und φ +dφ sowie den Polarwinkeln β und β +dβ aufgespannte Raumwinkelelement dΩ abgestrahlt wird.
Weiter sind h das plancksche Wirkungsquantum , c die Lichtgeschwindigkeit und k die Boltzmannkonstante .
Der Kosinusfaktor berücksichtigt den Umstand, dass bei Abstrahlung in eine beliebige durch φ und β gegebene Richtung nur die auf dieser Richtung senkrecht stehende Projektion
cos
(
β
)
d
A
{\displaystyle \cos(\beta )\mathrm {d} A}
A als effektive Strahlfläche auftritt. Die spektrale Strahldichte
L
Ω
ν
o
(
ν
,
T
)
{\displaystyle L_{\Omega \nu }^{o}(\nu ,T)}
Lambert-Strahler .
Bei der Umrechnung zwischen Frequenz- und Wellenlängendarstellung ist zu beachten, dass wegen
λ
=
c
ν
{\displaystyle \lambda ={\frac {c}{\nu }}}
gilt:
|
d
λ
|
=
c
ν
2
|
d
ν
|
{\displaystyle |\mathrm {d} \lambda |={\frac {c}{\nu ^{2}}}|\mathrm {d} \nu |}
und
|
d
ν
|
=
c
λ
2
|
d
λ
|
{\displaystyle |\mathrm {d} \nu |={\frac {c}{\lambda ^{2}}}|\mathrm {d} \lambda |}
Die spektrale Strahldichte ist eine spektrale gerichtete Größe.
Integriert man die spektrale Strahldichte über alle Richtungen des Halbraums, in welchen das betrachtete Flächenelement abstrahlt, so erhält man die spektrale spezifische Ausstrahlung in den Halbraum
M
ν
o
(
ν
,
T
)
{\displaystyle M_{\nu }^{o}(\nu ,T)}
M
ν
o
(
ν
,
T
)
d
A
d
ν
{\displaystyle M_{\nu }^{o}(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu }
=
∫
Halbraum
L
Ω
ν
o
(
ν
,
T
)
cos
(
β
)
d
A
d
ν
d
Ω
{\displaystyle =\int _{\text{Halbraum}}L_{\Omega \nu }^{o}(\nu ,T)\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \nu \,\mathrm {d} \Omega }
=
∫
φ
=
0
2
π
∫
β
=
0
π
2
L
Ω
ν
o
(
ν
,
T
)
cos
(
β
)
d
A
d
ν
sin
(
β
)
d
φ
d
β
{\displaystyle =\int _{\varphi =0}^{2\pi }\,\int _{\beta =0}^{\frac {\pi }{2}}L_{\Omega \nu }^{o}(\nu ,T)\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \nu \,\sin(\beta )\,\mathrm {d} \varphi \,\mathrm {d} \beta }
=
2
π
L
Ω
ν
o
(
ν
,
T
)
d
A
d
ν
∫
β
=
0
π
2
cos
(
β
)
sin
(
β
)
d
β
{\displaystyle =2\pi \,L_{\Omega \nu }^{o}(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu \int _{\beta =0}^{\frac {\pi }{2}}\cos(\beta )\sin(\beta )\,\mathrm {d} \beta }
=
π
L
Ω
ν
o
(
ν
,
T
)
d
A
d
ν
{\displaystyle =\pi \,L_{\Omega \nu }^{o}(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu }
so dass also
in der Frequenzdarstellung:
M
ν
o
(
ν
,
T
)
d
A
d
ν
=
2
π
h
ν
3
c
2
1
e
(
h
ν
k
T
)
−
1
d
A
d
ν
{\displaystyle M_{\nu }^{o}(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu \,={\frac {2\pi h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}\,\mathrm {d} A\,\mathrm {d} \nu }
SI-Einheit von
M
ν
o
(
ν
,
T
)
{\displaystyle M_{\nu }^{o}(\nu ,T)}
-2 Hz-1
und in der Wellenlängendarstellung:
M
λ
o
(
λ
,
T
)
d
A
d
λ
=
2
π
h
c
2
λ
5
1
e
(
h
c
λ
k
T
)
−
1
d
A
d
λ
{\displaystyle M_{\lambda }^{o}(\lambda ,T)\,\mathrm {d} A\,\mathrm {d} \lambda \,={\frac {2\pi hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}\,\mathrm {d} A\,\mathrm {d} \lambda }
SI-Einheit von
M
λ
o
(
λ
,
T
)
{\displaystyle M_{\lambda }^{o}(\lambda ,T)}
-2 μm-1 .
M
ν
o
(
ν
,
T
)
d
A
d
ν
{\displaystyle M_{\nu }^{o}(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu }
A im Frequenzbereich zwischen
ν
{\displaystyle \nu }
ν
+
d
ν
{\displaystyle \nu +d\nu }
Die spektrale spezifische Ausstrahlung ist eine spektrale hemisphärische Größe.
Integriert man die spektrale Strahldichte nicht über die Richtungen, sondern über alle Frequenzen, so erhält man die Gesamtstrahldichte
L
Ω
o
(
T
)
{\displaystyle L_{\Omega }^{o}(T)}
L
Ω
o
(
T
)
cos
(
β
)
d
A
d
Ω
=
∫
ν
=
0
∞
L
Ω
ν
o
(
ν
,
T
)
cos
(
β
)
d
A
d
ν
d
Ω
{\displaystyle L_{\Omega }^{o}(T)\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \Omega =\int _{\nu =0}^{\infty }L_{\Omega \nu }^{o}(\nu ,T)\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \nu \,\mathrm {d} \Omega }
Die Auswertung des Integrals liefert wegen
∫
0
∞
x
3
e
x
−
1
d
x
=
π
4
15
{\displaystyle \int _{0}^{\infty }{\frac {x^{3}}{e^{x}-1}}\,\mathrm {d} x={\frac {\pi ^{4}}{15}}}
L
Ω
o
(
T
)
cos
(
β
)
d
A
d
Ω
=
2
π
4
k
4
15
h
3
c
2
T
4
cos
(
β
)
d
A
d
Ω
{\displaystyle L_{\Omega }^{o}(T)\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \Omega ={\frac {2\pi ^{4}k^{4}}{15h^{3}c^{2}}}T^{4}\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \Omega }
SI-Einheit von
L
Ω
o
(
T
)
{\displaystyle L_{\Omega }^{o}(T)}
-2 sr-1 .
L
Ω
o
(
T
)
cos
(
β
)
d
A
d
Ω
{\displaystyle L_{\Omega }^{o}(T)\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \Omega }
A auf allen Frequenzen in das in der Richtung β gelegene Raumwinkelelement dΩ abgestrahlt wird.
Die Gesamtstrahldichte ist eine gerichtete Gesamtgröße.
Bearbeiten
spezifische Ausstrahlung
M
o
(
T
)
{\displaystyle \,M^{o}(T)}
M
o
(
T
)
d
A
{\displaystyle M^{o}(T)\,\mathrm {d} A}
=
∫
ν
=
0
∞
M
ν
o
(
ν
,
T
)
d
A
d
ν
{\displaystyle =\int _{\nu =0}^{\infty }M_{\nu }^{o}(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu }
≡
L
Ω
o
(
T
)
∫
Halbraum
cos
(
β
)
d
A
d
Ω
{\displaystyle \equiv L_{\Omega }^{o}(T)\int _{\text{Halbraum}}\cos(\beta )\,\mathrm {d} A\,\mathrm {d} \Omega }
=
π
L
Ω
o
(
T
)
d
A
s
r
{\displaystyle =\pi \,L_{\Omega }^{o}(T)\,\mathrm {d} A\,\mathrm {sr} }
so dass
M
o
(
T
)
d
A
=
σ
T
4
d
A
{\displaystyle M^{o}(T)\,\mathrm {d} A=\sigma \,T^{4}\,\mathrm {d} A}
SI-Einheit von
M
o
(
T
)
{\displaystyle \,M^{o}(T)}
-2 ,
mit der Stefan-Boltzmann-Konstanten
σ
=
2
π
5
k
4
15
h
3
c
2
=
(
5,670
400
±
0,000
040
)
⋅
10
−
8
W
m
2
K
4
{\displaystyle \sigma \,={\frac {2\pi ^{5}k^{4}}{15h^{3}c^{2}}}\,=(5{,}670400\pm 0{,}000040)\,\cdot \,10^{-8}\,\mathrm {\frac {W}{m^{2}K^{4}}} }
CODATA 2006). Bei Strahlung in ein Medium mit der Brechzahl
n
{\displaystyle n}
c
{\displaystyle c}
c
/
n
{\displaystyle c/n}
n
2
{\displaystyle n^{2}}
M
o
(
T
)
d
A
{\displaystyle M^{o}(T)\,\mathrm {d} A}
A auf allen Frequenzen in den Halbraum abgestrahlt wird.
Die spezifische Ausstrahlung ist eine hemisphärische Gesamtgröße.
Strahlungsfluss oder Strahlungsleistung
Bearbeiten
Integriert man die spezifische Ausstrahlung über die gesamte strahlende Fläche A , so erhält man die Strahlungsleistung
Φ
o
(
T
)
{\displaystyle \,\Phi ^{o}(T)}
Φ
o
(
T
)
=
∫
Fläche
M
o
(
T
)
d
A
{\displaystyle \Phi ^{o}(T)=\int _{\text{Fläche}}M^{o}(T)\,\mathrm {d} A}
so dass für einen Körper homogener Temperatur gilt
Φ
o
(
T
)
=
σ
T
4
A
{\displaystyle \Phi ^{o}(T)=\sigma \,T^{4}\,A}
SI-Einheit von
Φ
o
(
T
)
{\displaystyle \,\Phi ^{o}(T)}
Φ
o
(
T
)
{\displaystyle \Phi ^{o}(T)\,}
A auf allen Frequenzen in den Halbraum abgestrahlt wird.
Spektrale Energiedichte der Hohlraumstrahlung
Bearbeiten
Ein geschlossener Hohlraum mit Wänden aus beliebigem Material, welche auf der Temperatur T gehalten werden, ist nach Erreichen des thermischen Gleichgewichts mit einer homogenen isotropen thermischen Strahlung erfüllt, deren Eigenschaften nur von der Temperatur T abhängen und die daher universalen Charakter hat.
Bringt man einen kleinen Schwarzen Körper in den Hohlraum, so muss die Hohlraumstrahlung nach Wiederherstellung des thermischen Gleichgewichts die gleiche sein wie vorher, da sie nur von T abhängt. Da der Schwarze Körper sämtliche auf ihn treffende Hohlraumstrahlung absorbiert, zur Erhaltung des Gleichgewichts aber gleichzeitig die gleiche Strahlung als Ersatz wieder emittieren muss, müssen die spektralen Strahldichten der Hohlraumstrahlung und der Strahlung des Schwarzen Körpers identisch sein. Die oben hergeleiteten Ausdrücke für die einzelnen Strahlgrößen gelten daher auch für die Hohlraumstrahlung. Darüber hinaus weist die Hohlraumstrahlung eine konstante räumliche Energiedichte auf.
Man betrachte einen halbkugelförmigen mit Hohlraumstrahlung der Temperatur T gefüllten Hohlraum. Da die Strahlgrößen dieselben sind wie bei der Emission durch einen Schwarzen Körper, ist die aus dem gesamten Halbraum stammende auf ein Flächenelement dA im Mittelpunkt der kreisförmigen Grundfläche treffende Strahlungsleistung im Frequenzintervall zwischen ν und ν +dν gegeben durch die Formel zur spektralen spezifischen Ausstrahlung:
W
ν
(
ν
,
T
)
d
A
d
ν
=
M
ν
o
(
ν
,
T
)
d
A
d
ν
{\displaystyle W_{\nu }(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu =M_{\nu }^{o}(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu }
Seien nun
U
ν
o
d
ν
{\displaystyle U_{\nu }^{o}\,\mathrm {d} \nu }
ν und ν +dν und
n
ν
d
ν
{\displaystyle n_{\nu }\,\mathrm {d} \nu }
U
ν
o
d
ν
=
h
ν
⋅
n
ν
d
ν
{\displaystyle U_{\nu }^{o}\,\mathrm {d} \nu =h\nu \cdot n_{\nu }\,\mathrm {d} \nu }
Da die Strahlung isotrop ist, kommen alle Richtungen gleich häufig vor. Der Anteil an Photonen, welcher aus dem Raumwinkelelement dΩ , d. h. aus Richtungen zwischen φ und φ + dφ sowie zwischen β und β + dβ , stammt, ist gegeben durch das Verhältnis von dΩ zum vollen Raumwinkel 4π . Die Dichte an Photonen mit Frequenzen zwischen ν und ν +dν , welche aus dem Raumwinkel dΩ stammen, ist daher
n
ν
Ω
d
ν
d
Ω
=
n
ν
d
ν
d
Ω
4
π
=
n
ν
d
ν
sin
(
β
)
d
β
d
ϕ
4
π
{\displaystyle n_{\nu \Omega }\,\mathrm {d} \nu \,\mathrm {d} \Omega =n_{\nu }\,\mathrm {d} \nu {\frac {\mathrm {d} \Omega }{4\pi }}=n_{\nu }\,\mathrm {d} \nu {\frac {\sin(\beta )\mathrm {d} \beta \mathrm {d} \phi }{4\pi }}}
Von allen Photonen aus dem Frequenzintervall dν , welche aus der Richtung von dΩ kommen, treten jene durch die Fläche dA , welche sich in einem Zylinder befinden, der um den Winkel β in die Richtung von dΩ geneigt ist und dA zur Grundfläche hat. Pro Zeiteinheit dt treten jene Photonen durch dA , die sich in einem Zylinderstück der Länge c dt befinden. Sie treten also mit der Rate
n
ν
Ω
d
ν
d
Ω
⋅
cos
(
β
)
d
A
⋅
c
{\displaystyle n_{\nu \Omega }\,\mathrm {d} \nu \,\mathrm {d} \Omega \cdot \cos(\beta )\mathrm {d} A\cdot c}
durch dA . Da jedes Photon die Energie hν trägt, tritt die Energie mit der Rate
W
ν
Ω
(
ν
,
β
,
T
)
d
A
d
ν
d
Ω
=
h
ν
⋅
n
ν
Ω
d
ν
d
Ω
⋅
cos
(
β
)
d
A
⋅
c
=
h
ν
⋅
c
⋅
n
ν
d
ν
1
4
π
sin
(
β
)
cos
(
β
)
d
β
d
ϕ
d
A
{\displaystyle W_{\nu \Omega }(\nu ,\beta ,T)\,\mathrm {d} A\,\mathrm {d} \nu \,\mathrm {d} \Omega =h\nu \cdot n_{\nu \Omega }\,\mathrm {d} \nu \,\mathrm {d} \Omega \cdot \cos(\beta )\mathrm {d} A\cdot c=h\nu \cdot c\cdot n_{\nu }\,\mathrm {d} \nu {\frac {1}{4\pi }}\sin(\beta )\cos(\beta )\mathrm {d} \beta \,\mathrm {d} \phi \,\mathrm {d} A}
durch dA . Es treten Photonen aus dem gesamten oberen Halbraum durch dA ; Integration über den Halbraum liefert
W
ν
(
ν
,
T
)
d
A
d
ν
=
h
ν
⋅
c
⋅
n
ν
d
ν
1
4
π
∫
ϕ
=
0
2
π
∫
β
=
0
π
2
sin
(
β
)
cos
(
β
)
d
β
d
ϕ
d
A
=
h
ν
⋅
c
⋅
n
ν
d
ν
1
4
d
A
=
U
ν
o
c
4
d
A
d
ν
{\displaystyle W_{\nu }(\nu ,T)\,\mathrm {d} A\,\mathrm {d} \nu =h\nu \cdot c\cdot n_{\nu }\,\mathrm {d} \nu {\frac {1}{4\pi }}\int _{\phi =0}^{2\pi }\int _{\beta =0}^{\frac {\pi }{2}}\sin(\beta )\cos(\beta )\mathrm {d} \beta \,\mathrm {d} \phi \,\mathrm {d} A=h\nu \cdot c\cdot n_{\nu }\,\mathrm {d} \nu {\frac {1}{4}}\,\mathrm {d} A=U_{\nu }^{o}\,{\frac {c}{4}}\,\mathrm {d} A\,\mathrm {d} \nu }
Vergleich mit (*) zeigt:
U
ν
o
(
ν
,
T
)
=
4
c
⋅
M
ν
o
(
ν
,
T
)
{\displaystyle U_{\nu }^{o}(\nu ,T)={\frac {4}{c}}\cdot M_{\nu }^{o}(\nu ,T)}
Es gilt also
in der Frequenzdarstellung:
U
ν
o
(
ν
,
T
)
d
ν
d
V
=
8
π
h
ν
3
c
3
1
e
(
h
ν
k
T
)
−
1
d
ν
d
V
{\displaystyle U_{\nu }^{o}(\nu ,T)\,\mathrm {d} \nu \,\mathrm {d} V={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}\,\mathrm {d} \nu \,\mathrm {d} V}
SI-Einheit von
U
ν
o
(
ν
,
T
)
{\displaystyle U_{\nu }^{o}(\nu ,T)}
-3 s oder anschaulicher J m-3 Hz-1 ,
in der Wellenlängendarstellung:
U
λ
o
(
λ
,
T
)
d
λ
d
V
=
8
π
h
c
λ
5
1
e
(
h
c
λ
k
T
)
−
1
d
λ
d
V
{\displaystyle U_{\lambda }^{o}(\lambda ,T)\,\mathrm {d} \lambda \,\mathrm {d} V={\frac {8\pi hc}{\lambda ^{5}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}\,\mathrm {d} \lambda \,\mathrm {d} V}
SI-Einheit von
U
λ
o
(
λ
,
T
)
{\displaystyle U_{\lambda }^{o}(\lambda ,T)}
-4 oder anschaulicher J m-3 μm-1 .
U
ν
o
(
ν
,
T
)
d
ν
d
V
{\displaystyle U_{\nu }^{o}(\nu ,T)\,\mathrm {d} \nu \,\mathrm {d} V}
ν und ν + dν , welche sich im Volumenelement dV eines Hohlraumstrahlers befindet.
Gesamtenergiedichte der Hohlraumstrahlung
Bearbeiten
Integriert man die spektrale Energiedichte der Hohlraumstrahlung über alle Frequenzen, so erhält man die Gesamtenergiedichte
U
o
{\displaystyle U^{o}}
U
o
(
T
)
d
V
=
∫
ν
=
0
∞
U
ν
o
(
ν
,
T
)
d
ν
d
V
{\displaystyle U^{o}(T)\,\mathrm {d} V=\int _{\nu =0}^{\infty }U_{\nu }^{o}(\nu ,T)\,\mathrm {d} \nu \,\mathrm {d} V}
Auswertung des Integrals liefert:
U
o
(
T
)
d
V
=
σ
∗
T
4
d
V
{\displaystyle U^{o}(T)\,\mathrm {d} V\,=\sigma ^{*}\,T^{4}\,\mathrm {d} V}
mit
σ
∗
=
8
π
5
k
4
15
h
3
c
3
=
7
,
56
⋅
10
−
16
W
s
m
3
K
4
{\displaystyle \sigma ^{*}\,={\frac {8\pi ^{5}k^{4}}{15h^{3}c^{3}}}\,=7{,}56\,\cdot \,10^{-16}\,\mathrm {\frac {Ws}{m^{3}K^{4}}} }
U
o
(
T
)
{\displaystyle U^{o}(T)}
-3 .
U
o
(
T
)
d
V
{\displaystyle U^{o}(T)\,\mathrm {d} V}
V eines Hohlraumstrahlers befindet.
spektrale Strahldichte:
L
Ω
ν
o
(
ν
,
T
)
=
2
h
ν
3
c
2
1
e
(
h
ν
k
T
)
−
1
{\displaystyle L_{\Omega \nu }^{o}(\nu ,T)\,={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}}
L
Ω
λ
o
(
λ
,
T
)
=
2
h
c
2
λ
5
1
e
(
h
c
λ
k
T
)
−
1
{\displaystyle L_{\Omega \lambda }^{o}(\lambda ,T)\,={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}}
Einheit: W m-2 Hz-1 sr-1
Einheit: W m-2 m-1 sr-1
spektrale spezifische Ausstrahlung:
M
ν
o
(
ν
,
T
)
=
2
π
h
ν
3
c
2
1
e
(
h
ν
k
T
)
−
1
{\displaystyle M_{\nu }^{o}(\nu ,T)\,={\frac {2\pi h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}}
M
λ
o
(
λ
,
T
)
=
2
π
h
c
2
λ
5
1
e
(
h
c
λ
k
T
)
−
1
{\displaystyle M_{\lambda }^{o}(\lambda ,T)\,={\frac {2\pi hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}}
Einheit: W m-2 Hz-1
Einheit: W m-2 m-1
Gesamtstrahldichte:
L
Ω
o
(
T
)
=
2
π
4
k
4
15
h
3
c
2
T
4
{\displaystyle L_{\Omega }^{o}(T)={\frac {2\pi ^{4}k^{4}}{15h^{3}c^{2}}}T^{4}}
Einheit: W m-2 sr-1
spezifische Ausstrahlung ("Stefan-Boltzmann-Gesetz"):
M
o
(
T
)
=
σ
T
4
{\displaystyle M^{o}(T)\,=\sigma \,T^{4}}
Stefan-Boltzmann-Konstante
σ
=
2
π
5
k
4
15
h
3
c
2
=
5
,
67
⋅
10
−
8
W
m
2
K
4
{\displaystyle \sigma \,={\frac {2\pi ^{5}k^{4}}{15h^{3}c^{2}}}\,=5{,}67\,\cdot \,10^{-8}\,\mathrm {\frac {W}{m^{2}K^{4}}} }
Einheit: W m-2
spektrale Energiedichte im Hohlraum:
U
ν
o
(
ν
,
T
)
=
8
π
h
ν
3
c
3
1
e
(
h
ν
k
T
)
−
1
{\displaystyle U_{\nu }^{o}(\nu ,T)\,={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}}
U
λ
o
(
λ
,
T
)
=
8
π
h
c
λ
5
1
e
(
h
c
λ
k
T
)
−
1
{\displaystyle U_{\lambda }^{o}(\lambda ,T)\,={\frac {8\pi hc}{\lambda ^{5}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}}
Einheit: J m-3 Hz-1
Einheit: J m-3 m-1
Gesamtenergiedichte im Hohlraum:
U
o
(
T
)
=
σ
∗
T
4
{\displaystyle U^{o}(T)\,=\sigma ^{*}\,T^{4}}
σ
∗
=
8
π
5
k
4
15
h
3
c
3
=
7
,
56
⋅
10
−
16
J
m
3
K
4
{\displaystyle \sigma ^{*}\,={\frac {8\pi ^{5}k^{4}}{15h^{3}c^{3}}}\,=7{,}56\,\cdot \,10^{-16}\,\mathrm {\frac {J}{m^{3}K^{4}}} }
Einheit: J m-3
ν
{\displaystyle \nu }
λ
=
c
ν
{\displaystyle \lambda ={\frac {c}{\nu }}}
h
ν
{\displaystyle h\nu }
h
c
λ
{\displaystyle {\frac {hc}{\lambda }}}
[ 2]
spektrale Strahldichte:
L
~
Ω
ν
o
(
ν
,
T
)
=
2
ν
2
c
2
1
e
(
h
ν
k
T
)
−
1
{\displaystyle {\tilde {L}}_{\Omega \nu }^{o}(\nu ,T)\,={\frac {2\nu ^{2}}{c^{2}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}}
L
~
Ω
λ
o
(
λ
,
T
)
=
2
c
λ
4
1
e
(
h
c
λ
k
T
)
−
1
{\displaystyle {\tilde {L}}_{\Omega \lambda }^{o}(\lambda ,T)\,={\frac {2c}{\lambda ^{4}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}}
Einheit: Photonen s-1 m-2 Hz-1 sr-1
Einheit: Photonen s-1 m-2 m-1 sr-1
spektrale spezifische Ausstrahlung:
M
~
ν
o
(
ν
,
T
)
=
2
π
ν
2
c
2
1
e
(
h
ν
k
T
)
−
1
{\displaystyle {\tilde {M}}_{\nu }^{o}(\nu ,T)\,={\frac {2\pi \nu ^{2}}{c^{2}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}}
M
~
λ
o
(
λ
,
T
)
=
2
π
c
λ
4
1
e
(
h
c
λ
k
T
)
−
1
{\displaystyle {\tilde {M}}_{\lambda }^{o}(\lambda ,T)\,={\frac {2\pi c}{\lambda ^{4}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}}
Einheit: Photonen s-1 m-2 Hz-1
Einheit: Photonen s-1 m-2 m-1
Gesamtstrahldichte:
L
~
Ω
o
(
T
)
=
4
ζ
(
3
)
k
3
h
3
c
2
T
3
=
4,840
⋅
10
14
1
s
m
2
s
r
K
3
⋅
T
3
{\displaystyle {\tilde {L}}_{\Omega }^{o}(T)={\frac {4\zeta (3)k^{3}}{h^{3}c^{2}}}\,T^{3}=4{,}840\cdot 10^{14}\mathrm {\frac {1}{s\,m^{2}\,sr\,K^{3}}} \,\cdot \,T^{3}}
mit
ζ
(
3
)
=
1,202
056903
…
{\displaystyle \zeta (3)=1{,}202056903\dots }
riemannsche Zeta-Funktion bzw. Apery -Konstante)
Einheit: Photonen s-1 m-2 sr-1
spezifische Ausstrahlung (Stefan-Boltzmann-Gesetz für die Photonenrate):
M
~
o
(
T
)
=
4
π
ζ
(
3
)
k
3
h
3
c
2
T
3
=
1,520
4
⋅
10
15
1
s
m
2
K
3
⋅
T
3
{\displaystyle {\tilde {M}}^{o}(T)\,={\frac {4\pi \zeta (3)k^{3}}{h^{3}c^{2}}}\,T^{3}=1{,}5204\cdot 10^{15}\mathrm {\frac {1}{s\,m^{2}\,K^{3}}} \,\cdot \,T^{3}}
Einheit: Photonen s-1 m-2
spektrale Photonendichte im Hohlraum:
U
~
ν
o
(
ν
,
T
)
=
8
π
ν
2
c
3
1
e
(
h
ν
k
T
)
−
1
{\displaystyle {\tilde {U}}_{\nu }^{o}(\nu ,T)\,={\frac {8\pi \nu ^{2}}{c^{3}}}{\frac {1}{e^{\left({\frac {h\nu }{kT}}\right)}-1}}}
U
~
λ
o
(
λ
,
T
)
=
8
π
λ
4
1
e
(
h
c
λ
k
T
)
−
1
{\displaystyle {\tilde {U}}_{\lambda }^{o}(\lambda ,T)\,={\frac {8\pi }{\lambda ^{4}}}{\frac {1}{e^{\left({\frac {hc}{\lambda kT}}\right)}-1}}}
Einheit: Photonen m-3 Hz-1
Einheit: Photonen m-3 m-1
Gesamtphotonendichte im Hohlraum:
U
~
o
(
T
)
=
16
π
ζ
(
3
)
k
3
h
3
c
3
T
3
=
2,029
⋅
10
7
1
m
3
K
3
⋅
T
3
{\displaystyle {\tilde {U}}^{o}(T)\,={\frac {16\pi \zeta (3)k^{3}}{h^{3}c^{3}}}\,T^{3}=2{,}029\cdot 10^{7}\,\mathrm {\frac {1}{m^{3}K^{3}}} \,\cdot \,T^{3}}
Einheit: Photonen m-3
↑ Baehr/Stephan, S. 591
↑ Tatum
Baehr/Stephan: Baehr H.D., Stephan K.: Wärme- und Stoffübertragung . 5. Auflage, Springer, Berlin 2006, ISBN 978-3-540-32334-1
Tatum: Tatum J.B.: Stellar Atmospheres , chapter 2: Blackbody Radiation . On-line lecture notes (pdf 217 KB)
Es existieren zwei Operatoren, die sich direkt auf eine physikalische Größe auswirken, ohne sie zu verändern:
Einheit-Von-Operator: (Kraftbeispiel) [1,5 N] = [F] = N
Skalar-Von-Operator: (Kraftbeispiel) {1,5 N} = 1,5 Man beachte in dem Zusammenhang, dass insbesondere im amerikanischen Raum diese Operatoren anders verwendet werden, insbesondere schreibt man dort oft die Einheit in Eckige Klammern, zum Beispiel [N].
Jede physikalische Größe läßt sich aus einem Zahlenwert und einer Einheit schreiben.
physikalische Größe = Zahlenwert * Einheit Beispiel:
7 Meter = 7 * Meter
Basisgröße
Formelzeichen
Symbol für Dimension
Basiseinheit
Einheitenzeichen
Definition der Einheit
Länge
l
{\displaystyle l\,}
s
{\displaystyle s\,}
x
{\displaystyle x\,}
r
{\displaystyle r\,}
L
Meter
m
{\displaystyle \mathrm {m} \,}
Länge der Strecke, die das Licht im Vakuum während einer der Dauer von (1/299 792 458) Sekunden durchläuft
Masse
m
{\displaystyle m\,}
M
Kilogramm
k
g
{\displaystyle \mathrm {kg} \,}
Einheit der Masse; es ist gleich der Masse des Internationalen Kilogrammprototyps
Zeit
t
{\displaystyle t\,}
T
Sekunde
s
{\displaystyle \mathrm {s} \,}
das 9 192 631 770fache der Periodendauer der dem Übergang zwischen den beiden Hyperfeinstrukturniveaus des Grundzustandes von Atomen des Nuklids 133 Cs entsprechenden Strahlung
elektrische Stromstärke
I
{\displaystyle I\,}
I
Ampere
A
{\displaystyle \mathrm {A} \,}
Stärke eines konstanten Stromes, der, durch zwei parallele, geradlinige, unendlich lange und im Vakuum im Abstand von einem Meter voneinander angeordnete Elektrische Leiter von vernachlässigbar kleinem, kreisförmigem Querschnitt fließend, zwischen diesen Leitern je einem Meter Leiterlänge die Kraft 2 · 10 −7 Newton hervorruft.
Absolute Temperatur (auch thermodynamische Temperatur )
T
{\displaystyle T\,}
θ
Kelvin
K
{\displaystyle \mathrm {K} \,}
der 273,16te Teil der thermodynamischen Temperatur des Tripelpunktes des Wassers1
Stoffmenge
n
{\displaystyle n\,}
N
Mol
m
o
l
{\displaystyle \mathrm {mol} \,}
die Stoffmenge eines Systems, das aus ebensoviel Einzelteilchen besteht, wie Atome in 0,012 Kilogramm des Kohlenstoffnuklids 12 C enthalten sind. Bei Benutzung des Mol müssen die Einzelteilchen spezifiziert sein und können Atome, Moleküle, Ionen, Elektronen sowie anderer Teilchen oder Gruppen solcher Teilchen genau angegebener Zusammensetzung sein.
Lichtstärke
I
V
{\displaystyle I_{\mathrm {V} }\,}
J
Candela
c
d
{\displaystyle \mathrm {cd} \,}
Lichtstärke in einer bestimmten Richtung einer Strahlungsquelle, die monochromatische Strahlung der Frequenz 540 · 1012 Hertz aussendet und deren Strahlstärke in dieser Richtung (1/683) Watt durch Steradiant beträgt.
1) Zwischen der thermodynamischen Temperatur T und der Celsiustemperatur t besteht der Zusammenhang: t /°C = T /K + 273,15
Größe
Formelzeichen
Einheit
Einheitenzeichen
in SI-Basiseinheiten
Raumwinkel
Ω
{\displaystyle \Omega \ }
Steradiant
sr
m
2
m
2
{\displaystyle {\frac {\mathrm {m} ^{2}}{\mathrm {m} ^{2}}}\ }
2), 3)
Frequenz
f
{\displaystyle f\ }
Hertz
Hz
1
s
{\displaystyle {\frac {1}{\mathrm {s} }}\ }
Geschwindigkeit
v
{\displaystyle v\ }
Meter pro Sekunde
m/s
m
s
{\displaystyle {\frac {\mathrm {m} }{\mathrm {s} }}\ }
Beschleunigung
a
{\displaystyle a\ }
Meter pro Sekunde2
m/s2
m
s
2
{\displaystyle {\frac {\mathrm {m} }{\mathrm {s} ^{2}}}\ }
Kraft
F
{\displaystyle F\ }
Newton
N
k
g
⋅
m
s
2
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} ^{2}}}\ }
Druck
p
{\displaystyle p\ }
Pascal
Pa
k
g
s
2
⋅
m
=
N
m
2
{\displaystyle {\frac {\mathrm {kg} }{\mathrm {s} ^{2}\cdot \mathrm {m} }}={\frac {\mathrm {N} }{\mathrm {m} ^{2}}}\ }
Impuls
p
{\displaystyle p\ }
Newtonsekunde
Ns
k
g
⋅
m
s
=
N
⋅
s
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} }}=\mathrm {N} \cdot \mathrm {s} \ }
Arbeit, Energie
W
,
E
{\displaystyle W,E\ }
Joule
J
k
g
⋅
m
2
s
2
=
W
⋅
s
=
N
⋅
m
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{2}}}=\mathrm {W} \cdot \mathrm {s} =\mathrm {N} \cdot \mathrm {m} \ }
Leistung
P
{\displaystyle P\ }
Watt
W
k
g
⋅
m
2
s
3
=
N
⋅
m
s
=
J
s
=
V
⋅
A
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{3}}}=\mathrm {N} \cdot {\frac {\mathrm {m} }{\mathrm {s} }}={\frac {\mathrm {J} }{\mathrm {s} }}=\mathrm {V} \cdot \mathrm {A} \ }
elektrische Spannung (elektrisches Potential)
U
{\displaystyle U\ }
Volt
V
k
g
⋅
m
2
s
3
⋅
A
=
W
A
=
J
C
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{3}\cdot \mathrm {A} }}={\frac {\mathrm {W} }{\mathrm {A} }}={\frac {\mathrm {J} }{\mathrm {C} }}\ }
elektrische Ladung
Q
{\displaystyle Q\ }
Coulomb
C
A
⋅
s
{\displaystyle \mathrm {A} \cdot \mathrm {s} \ }
magnetischer Fluss
Φ
{\displaystyle \Phi \ }
Weber
Wb
k
g
⋅
m
2
s
2
⋅
A
=
V
⋅
s
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{2}\cdot \mathrm {A} }}=\mathrm {V} \cdot \mathrm {s} \ }
elektrischer Widerstand
R
{\displaystyle R\ }
Ohm
Ω
k
g
⋅
m
2
s
3
⋅
A
2
=
V
A
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{3}\cdot \mathrm {A} ^{2}}}={\frac {\mathrm {V} }{\mathrm {A} }}\ }
elektrischer Leitwert
G
{\displaystyle G\ }
Siemens
S
s
3
⋅
A
2
k
g
⋅
m
2
=
1
Ω
{\displaystyle {\frac {\mathrm {s} ^{3}\cdot \mathrm {A} ^{2}}{\mathrm {kg} \cdot \mathrm {m} ^{2}}}={\frac {1}{\Omega }}\ }
Induktivität
L
{\displaystyle L\ }
Henry
H
k
g
⋅
m
2
s
2
⋅
A
2
=
W
b
A
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{2}\cdot \mathrm {A} ^{2}}}={\frac {\mathrm {Wb} }{\mathrm {A} }}\ }
elektrische Kapazität
C
{\displaystyle C\ }
Farad
F
A
2
⋅
s
4
k
g
⋅
m
2
=
C
V
{\displaystyle {\frac {\mathrm {A} ^{2}\cdot \mathrm {s} ^{4}}{\mathrm {kg} \cdot \mathrm {m} ^{2}}}={\frac {\mathrm {C} }{\mathrm {V} }}\ }
magnetische Flussdichte, Induktion
B
{\displaystyle B\ }
Tesla
T
k
g
s
2
⋅
A
=
W
b
m
2
{\displaystyle {\frac {\mathrm {kg} }{\mathrm {s} ^{2}\cdot \mathrm {A} }}={\frac {\mathrm {Wb} }{\mathrm {m} ^{2}}}\ }
Elektrische Feldstärke
E
{\displaystyle E\ }
Volt pro Meter oder
V/m oder
k
g
⋅
m
s
3
⋅
A
=
N
C
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} ^{3}\cdot \mathrm {A} }}={\frac {\mathrm {N} }{\mathrm {C} }}\ }
Magnetische Feldstärke, magn. Erregung
H
{\displaystyle H\ }
Ampere pro Meter
A/m
A
m
{\displaystyle {\frac {\mathrm {A} }{\mathrm {m} }}\ }
Elektrische Flussdichte, el. Verschiebungsdichte, el. Erregung
D
{\displaystyle D\ }
Coulomb pro Quadratmeter
C/m2
A
⋅
s
m
2
{\displaystyle {\frac {\mathrm {A} \cdot \mathrm {s} }{\mathrm {m} ^{2}}}\ }
Permittivität
ε
{\displaystyle \varepsilon \ }
Farad pro Meter
F/m
A
2
⋅
s
4
k
g
⋅
m
3
=
A
⋅
s
V
⋅
m
{\displaystyle {\frac {\mathrm {A} ^{2}\cdot \mathrm {s} ^{4}}{\mathrm {kg} \cdot \mathrm {m} ^{3}}}={\frac {\mathrm {A} \cdot \mathrm {s} }{\mathrm {V} \cdot \mathrm {m} }}\ }
Permeabilität (Magnetismus)
μ
{\displaystyle \mu \ }
Henry pro Meter
H/m
k
g
⋅
m
s
2
⋅
A
2
=
V
⋅
s
A
⋅
m
{\displaystyle {\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} ^{2}\cdot \mathrm {A} ^{2}}}={\frac {\mathrm {V} \cdot \mathrm {s} }{\mathrm {A} \cdot \mathrm {m} }}\ }
Lichtstrom
Φ
ν
{\displaystyle \Phi _{\nu }\ }
Lumen
lm
c
d
⋅
s
r
{\displaystyle \mathrm {cd} \cdot \mathrm {sr} \ }
Beleuchtungsstärke
E
ν
{\displaystyle E_{\nu }\ }
lux
lx
c
d
⋅
s
r
m
2
=
l
m
m
2
{\displaystyle {\frac {\mathrm {cd} \cdot \mathrm {sr} }{\mathrm {m} ^{2}}}={\frac {\mathrm {lm} }{\mathrm {m} ^{2}}}\ }
Fläche
A
{\displaystyle A\ }
Quadratmeter
m2
m
2
{\displaystyle \mathrm {m} ^{2}\ }
Volumen
V
{\displaystyle V\ }
Kubikmeter
m3
m
3
{\displaystyle \mathrm {m} ^{3}\ }
Dichte
ρ
{\displaystyle \rho \ }
Tonne pro Kubikmeter;
t/m3 ;
t
m
3
{\displaystyle {\frac {\mathrm {t} }{\mathrm {m} ^{3}}}\ }
Gramm pro Kubikzentimeter;
g/cm3 ;
g
c
m
3
{\displaystyle {\frac {\mathrm {g} }{\mathrm {cm} ^{3}}}\ }
Kreisfrequenz
ω
{\displaystyle \omega \ }
Hertz
Hz
1
s
{\displaystyle {\frac {\mathrm {1} }{\mathrm {s} }}\ }
Radioaktivität
A
{\displaystyle A\ }
Becquerel (Einheit)
Bq
1
s
{\displaystyle {\frac {1}{\mathrm {s} }}\ }
Dosis
D
{\displaystyle D\ }
Gray
Gy
J
k
g
{\displaystyle {\frac {\mathrm {J} }{\mathrm {kg} }}\ }
Entropie
S
{\displaystyle S\ }
Joule pro Kelvin bzw. Grad Celsius
J/K bzw. J/°C
J
K
{\displaystyle {\frac {\mathrm {J} }{\mathrm {K} }}\ }
katalytische Aktivität
z
{\displaystyle z\ }
Katal
kat
m
o
l
s
{\displaystyle {\frac {\mathrm {mol} }{\mathrm {s} }}\ }
1) Grad (°), 1° = (π/180) rad, ist keine SI-Einheit, die Verwendung, auch in Kombination mit SI-Einheiten, ist jedoch nach BIPM zulässig. Anders als bei SI-Einheiten wird bei Gradangaben ebener Winkel vor dem Gradzeichen kein Leerzeichen geschrieben.
2) Bei Verhältnisgrößen bestünde prinzipiell die Möglichkeit, die Einheiten zu kürzen und den Quotienten durch 1 zu ersetzen. Diese Kürzung unterbleibt jedoch, um zu vermeiden, dass verschiedenartige Größen gleichbenannte Einheiten erhalten. Der durch die Kürzung bewirkte Informationsverlust führt zu Mehrdeutigkeiten. Deshalb wird z. B. der Alkoholgehalt bei Getränken nicht einfach in % (Prozent), sondern in Vol% (Volumen-Prozent) angegeben – sonst wäre eine Abgrenzung zu z. B. Gew% (Gewichts-Prozent) nicht möglich.
3) In der Lichttechnik wird der Raumwinkel allgemein nicht als abgeleitete SI-Einheit betrachtet, sondern als Basis-SI-Einheit.
4) Neben Pascal ist auch die Angabe des Drucks laut BIPM in Bar zulässig.
Vorsatz
Bedeutung
Zeichen
Multiplikationsfaktor
Yotta
Quadrillion
Y
1024
Zetta
Trilliarde
Z
1021
Exa
Trillion
E
1018
Peta
Billiarde
P
1015
Tera
Billion
T
1012 = 1 000 000 000 000
Giga
Milliarde
G
109 = 1 000 000 000
Mega
Million
M
106 = 1 000 000
Kilo
Tausend
k
103 = 1000
Hekto
Hundert
h
102 = 100
Deka
Zehn
da
101 = 10
Dezi
Zehntel
d
10−1 = 0,1
Zenti
Hundertstel
c
10−2 = 0,01
Milli
Tausendstel
m
10−3 = 0,001
Mikro
Millionstel
µ
10−6 = 0,000 001
Nano
Milliardstel
n
10−9 = 0,000 000 001
Pico
Billionstel
p
10−12 = 0,000 000 000 001
Femto
Billiardstel
f
10−15
Atto
Trillionstel
a
10−18
Zepto
Trilliardstel
z
10−21
Yokto
Quadrillionstel
y
10−24
Bezeichnung der Konstante
Symbol(e)
Wert
Elektromagnetismus
Elementarladung
e
1,602 176 462(63) · 10−19 C
Permeabilität (Magnetismus) des Vakuums
μ 0
4π · 10−7 H m−1 (definiert)12,566370614 · 10−7 T 2 m3 J −1
Dielektrizitätskonstante des Vakuums
ε 0 = 1/(μ 0 c 0 2 )
8,854 187 816 · 10−12 F m−1
Lichtgeschwindigkeit im Vakuum
c 0
299 792 458 m s−1 (definiert)
Gravitation
Gravitationskonstante
G
6,672 42(10) · 10−11 m 3 kg −1 s −2
(Norm-)Fallbeschleunigung, (Norm-)Erdbeschleunigung
g n
9,80665 m s −2 (definiert)
Thermodynamik
Avogadrozahl oder Loschmidt-Zahl
L , N A , N L
6,022 141 99(47) · 1023 mol −1
Boltzmann-Konstante
k B
1,380 650 3(24) · 10−23 J K −1
8,617 342(15) · 10−5 eV K −1
Universelle Gaskonstante
R 0 = N A k B
8,314 472 (15) J K −1 mol −1
Stefan-Boltzmann-Konstante
σ
5,670 51(19) · 10−8 W m −2 K −4
Absoluter Nullpunkt
−273,15 °C = 0 K
Molvolumen eines idealen Gases, p = 1 bar, θ = 0 °C
22,413 996(39) L mol −1
Standard-Atmosphärendruck
atm
101 325 Pa (definiert)
Elementarteilchen
Planck'sche Konstante bzw. Wirkungsquantum
h
6,626 068 76(52) · 10−34 J s
4,135 667 27(52) · 10−15 eV s
ħ = h /(2π)
1,054 571 596(82) · 10−34 J s
Feinstrukturkonstante
α = μ 0 e 2 c 0 / (2h )
7,297 352 533(27) · 10−3
α −1
137,035 999 76(50)
Ruhemasse des Elektrons
m e
9,109 381 88(72) · 10−31 kg
Klassischer Elektronenradius
r e
2,817 92 · 10−15 m
Ruhemasse des Protons
m p
1,672 621 58(13) · 10−27 kg
Ruhemasse des Neutrons
m n
1,674 928 6(10) · 10−27 kg
Gyromagnetisches Verhältnis des freien Elektrons
γ e
1,760 859 2 · 1011 s −1 T −1
Rydbergkonstante
R ∞
1,097 373 153 4(13) · 107 m −1
Rydbergfrequenz
R ∞ c
3,289 841 960 360 · 1015 s −1
Rydbergenergie
R ∞ ch
13,605 141 384 3(13) eV
Bohrscher Radius
a 0 0,529 177 208 3(19) · 10−10 m
Bohrsches Magneton
μ B
9,274 015 4(31) · 10−24 J T −1
Magnetisches Moment des Elektrons
μ e
−9,284 770 1(31) · 10−24 J T −1
Landé-g -Faktor des freien Elektrons
g e
2,002 319 304 386(20)
Nukleares Magneton, Kernmagneton
μ N
5,050 786 6(17) · 10−27 J T −1
Magnetisches Moment des Protons
μ p
1,410 607 61(47) · 10−26 J T −1
Gyromagnetisches Verhältnis des Protons
γ p
2,675 221 28(81) · 108 s−1 T −1
Magnetisches Moment des Protons in H2 O
μ' p /μ B
1,520 993 129(17) · 10−3
Resonanzfrequenz des Protons per Feld in H2 O
γ' p /2π
42,576 375 (13) MHz T −1
Vermischtes
Atomare Masseneinheit
m u , amu, 1u
1,660 538 73(13) · 10−27 kg
Faradaysche Konstante
F
9,648 530 9(29) · 104 C mol −1
Magnetisches Flussquantum
Φ 0 =h /(2e )
2,06783364 · 10−15 Wb
Hartree-Energie
E h
4,359 748 2(26) · 10−18 J
Erste Strahlungskonstante
c 1
3,741 774 9(22) · 10−16 W m 2
Zweite Strahlungskonstante
c 2
1,438 769 (12) · 10−2 m K
Die Ziffern in Klammern hinter einem Zahlenwert bezeichnen die
Unsicherheit in den letzten Stellen des Wertes. (Beispiel: Die Angabe
6,672 42(10) ist gleichbedeutend mit 6,672 42 ± 0,000 10.) Die Unsicherheit ist
als einfache Standardabweichung gegeben.








































































































![{\displaystyle [F]=\mathrm {N} :={\frac {\mathrm {kg} \cdot \mathrm {m} }{\mathrm {s} ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dd8a5501aee085e2422852493f23452c20c8748)










![{\displaystyle [W]=\mathrm {J} :={\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{2}}}=\mathrm {N} \cdot \mathrm {m} =\mathrm {W} \cdot \mathrm {s} =\mathrm {V} \cdot \mathrm {A} \cdot s=\mathrm {V} \cdot \mathrm {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc08e8162c310169b928bf4f39c7fc02606163b7)




































![{\displaystyle T=\left[t_{1},t_{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67845b4a339649bdc5978994b3d994d8fa0fac4e)

























































![{\displaystyle h(t)=H-{\frac {m}{\alpha }}\ln \left[\cosh \left({\sqrt {\frac {\alpha g}{m}}}\cdot t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea40996844a65911d1238d425bd3561c7c54a2c)






![{\displaystyle h(t)=H+{\frac {m}{\alpha }}g\left[{\frac {m}{\alpha }}\left(1-e^{-(\alpha /m)t}\right)-t\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd73e10feb3029b7ec31f79c38af5943d7062a5a)




















































































































































































































































































































![{\displaystyle [Q]=[I]\cdot [t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d272f22a20b4dd4d70d4a8e8086e9a4417e99904)






































































![{\displaystyle [\rho ]={\frac {\Omega \cdot \mathrm {mm} ^{2}}{\mathrm {m} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d47846bced2faa5beea2f326078d4a3a1ae804c)

![{\displaystyle [\gamma ]={\frac {\mathrm {m} }{\Omega \cdot \mathrm {mm} ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/235fa819883eb440291d9b6295c3d075454a2076)











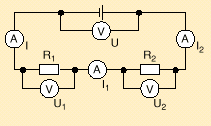














![{\displaystyle [{\vec {B}}]={\frac {[U]\cdot [t]}{[s]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/666137bc52825a822daf81fefa045c509442c2bd)
















![{\displaystyle [H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d2226487b5eb5f8a607d7233b5825b05775db6)





![{\displaystyle [\Phi ]=[U]\cdot [t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf3a5d32aea08520e3be38393c644840cbce26cb)


![{\displaystyle [L]={\frac {[\Phi ]}{[I]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6e6b5049fb3a19e5682854f16cf5dac20a988f8)















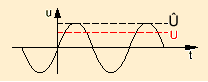




















![{\displaystyle {\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3ba2638d05cd9ed8dafae7e34986399e48ea99)


















































![{\displaystyle [C]=1\,\mathrm {F} ={\frac {\mathrm {C} }{\mathrm {V} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a7912d312301c6ef4126ed318476ee14bae7efb)




























































































































![{\displaystyle \nu =\left\{{\begin{matrix}1&{\mbox{wenn}}\ GR\leq GR_{\mathrm {M} }\\{\sqrt[{3}]{2}}+\left(1-{\sqrt[{3}]{2}}\right){\frac {GR_{\mathrm {M} }}{GR}}&{\mbox{sonst}}\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b01f4c2e8a55b39e5e7db446336ea613629cd159)





![{\displaystyle D_{p}=D_{p,\mathrm {unmod} }\left(1{,}16\,\exp \left(-\left[{\frac {{\frac {H}{0{,}3048}}-156}{1062}}\right]\right)\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed0f892c2ea74ee4579d70bc406184ae48dc3f5)







![{\displaystyle {\mathit {OP}}(r)={\mathit {OP}}_{\mathrm {DNA} }(r/{\sqrt[{3}]{2}})\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82621592a3e77be0fc113f8ccd127659121b8d76)





![{\displaystyle R(t)=\left[\left(R_{-4}t^{C}\right)^{-3}+R_{\infty }^{-3}\right]^{-1/3}\ ;\quad R_{-4}=13\,\mathrm {m} \ ;\ R_{\infty }=236\,\mathrm {m} \ ;\ C=0{,}406\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aa73ad4587b3a9670ff0d144984abb729ddb507)
![{\displaystyle R(t,W)=\left[\left(S_{0}W_{\mathrm {b} }^{(1-C)/3}R_{0}t^{C}\right)^{-3}+\left(S_{\infty }W_{\mathrm {h} }^{0{,}39}R_{\infty }\right)^{-3}\right]^{-1/3}\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18043a761e4333817fb4433ee9db23b8ee51a3df)






![{\displaystyle R(t,W)=\left[\left(\left[{\frac {W_{\mathrm {b} }}{S_{P}}}\right]^{0{,}198}S_{T}^{0{,}203}R_{0}t^{0{,}406}\right)^{-3}+\left(W_{\mathrm {h} }^{0{,}39}S_{P}^{-0{,}2}R_{\infty }\right)^{-3}\right]^{-1/3}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/018b6d89f8e4548f40caacf2a8bc1dd66523419e)





























































![{\displaystyle \left[{\frac {P}{P_{kr}}}+3\left({\frac {v_{kr}}{v}}\right)^{2}\right]\left[3{\frac {v}{v_{kr}}}-1\right]=8{\frac {T}{T_{kr}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea3a178809455d43fc13e2344ff7f915bbd3c356)


















































































































































































