LaTeX

Elemente
Bearbeiten

Es gibt Geometrie in der Ebene (2D) und im Raum (3D). Planimetrie ist die Geometrie in der Ebene. Die fundamentalen Elemente der Geometrie sind Punkt, Gerade, Strecke, Strahl, Winkel und Ebene.
- Als Punkt wird in der Geometrie ein Objekt ohne Ausdehnung verstanden. Siehe Punkt
- Eine Gerade ist eine unendlich lange, unendlich dünne und in beide Richtungen unbegrenzte Linie konstanter Ausrichtung. Siehe Gerade
- Eine Strecke ist ein von zwei Punkten begrenzter Teil einer Gerade. Siehe Strecke
- Ein Strahl ist eine von einem Punkt einseitig begrenzter Teil einer Gerade. Siehe Strahl
- Die Ebene ist ein unbegrenzt ausgedehntes flaches zweidimensionales Objekt. Siehe Ebene
- Ein Winkel ist ein Teil der Ebene, der von zwei in der Ebene liegenden Strahlen (Halbgeraden) mit gemeinsamem Anfangspunkt begrenzt wird. Siehe Winkel
Grundkonstruktionen
Bearbeiten

Hier werden wichtige Grundkonstruktionen der ebenen Geometrie erläutert. Es geht hier um Konstruktionen mit klassischen Mitteln, also nur Zirkel und (unskaliertes) Lineal.
Aufbau des Systems
BearbeitenVoraussetzung für alle Konstruktionen sind die beiden Elementarkonstruktionen "Strecke abtragen" und "Winkel antragen", deren Funktionsweise sich direkt erschließt. Darauf bauen die beiden wichtigsten Grundkonstruktionen "Halbieren einer Strecke" und "Halbieren eines Winkels" auf. Diese wiederum sind die Basis für die Konstruktion von Senkrechten und Parallelen.
Elementarkonstruktionen
BearbeitenAbtragen einer Strecke auf einer Geraden
Bearbeiten- Gegeben: Eine Strecke AB und eine Gerade mit einem Punkt P darauf.
- Mit dem Zirkel in Punkt A einstecken und den Abstand zu B einstellen.
- Den Zirkel in Punkt P einstecken und die Schnittpunkte des Kreises mit der Geraden zeichnen.
- Es gibt zwei (!) Möglichkeiten.
Antragen eines Winkels in einem Punkt an eine Gerade
Bearbeiten
- Gegeben: Ein Winkel α und eine Gerade mit einem Punkt P darauf.
- Mit dem Zirkel in den Scheitelpunkt S des Winkels einstecken und einen Bogen durch beide Schenkel zeichnen (Punkte A und B).
- Den gleichen Bogen auch um den Punkt P der Geraden zeichnen. Es ergibt sich Punkt C .
- Den Zirkel auf den Abstand der beiden Punkte A und B einstellen und einen Bogen um C zeichnen.
- Die Schnittpunkte der beiden Kreise um P und C ergibt den möglichen Punkt D auf dem anderen Schenkel des Winkels.
- Es gibt durch zweifache Spiegelung vier (!) Möglichkeiten.
Grundkonstruktionen erster Stufe
BearbeitenHalbieren einer Strecke (Mittelsenkrechte, Streckensymmetrale)
Bearbeiten
- Gegeben: Eine Strecke AB
- Zeichne um den Punkt A einen Bogen mit einem Radius größer als AB / 2 .
- Zeichne um den Punkt B einen Bogen mit dem gleichen Radius.
- Verbinde die Schnittpunkte der Bögen( P und Q) mit einer Geraden. Diese halbiert AB in Punkt M und ist senkrecht zu AB.
Halbieren eines Winkels
Bearbeiten
- Gegeben: Ein Winkel α
- Zeichne um den Scheitelpunkt S einen Bogen mit beliebigem Radius. Die Schnittpunkte sind A und B .
- Zwei weitere Bögen mit je ausreichendem Radius schneiden sich in einem weiteren Punkt C.
- Die Gerade durch S und C halbiert den Winkel.
| Hinweis |
| Die beiden Bögen um die Punkte A und B müssen den gleichen Radius haben. Dieser darf jedoch vom Radius des Bogens um S abweichen. Je größer die gewählten Radien, um so genauer wird die Konstruktion. |
Grundkonstruktionen zweiter Stufe
BearbeitenSpiegelung eines Punktes an einer Geraden (Fällen des Lotes)
Bearbeiten
- Gegeben: Eine Gerade g und ein Punkt P außerhalb der Gerade.
- Zeichne um zwei verschiedene Punkte (A , B) der Gerade jeweils einen Bogen vom Punkt P auf die andere Seite.
- Der andere Schnittpunkt ist die Spiegelung P' des Punktes P an der Geraden.
- Verbinde die Punkte mit einer Geraden. Diese ist das Lot von P auf die Gerade g mit dem Fußpunkt F.
| Hinweis |
| Die in vielen Lehrbüchern dargestellte Konstruktion mit zwei gleichen Radien ist mathem. nicht notwendig und nur sinnvoll, wenn der Punkt so nahe an der Gerade liegt, dass die Konstruktion zu ungenau wird. Siehe dazu auch unter "Errichten einer Senkrechten" auf einem Punkt. |
Errichten einer Senkrechten zu einer Geraden (Errichten des Lotes)
Bearbeiten
Linke Bildhälfte:
- Gegeben: Eine Gerade g und ein Punkt M auf der Gerade.
- Markiere mit dem Zirkel von dem Punkt M aus zwei weitere Punkte mit gleichem Abstand zu M auf der Gerade (A, B)
- Zeichne um diese Punkte jeweils einen Kreis mit größerem Radius als zuerst mit dem Zirkel abgetragen.
- Die Gerade durch M und den Schnittpunkt S der Kreise ist die Senkrechte s zu g im Punkt M und die Mittelsenkrechte der Stecke AB.
Rechte Bildhälfte:
Dieses Verfahren ist auch geeignet, Das Lot auf eine Gerade zu fällen, wenn der geg. Punkt nahe an der Gerade liegt.
Parallele in vorgegebenem Abstand
Bearbeiten
- Gegeben: Eine Gerade g1 und ein Abstand d.
- In zwei beliebigen aber verschiedenen Punkten P und Q der Gerade g1 werden die Senkrechten s1 und s2 errichtet.
- Trage auf den Senkrechten ( auf einer Seite der Gerade g1) jeweils den Abstand d ab.
- Die Gerade g2 durch die so gefundenen Punkte R und S ist zu g1 parallel und hat den Abstand PR = QS = d.
| Hinweis |
| Je länger die Strecke PQ gewählt wird, desto genauer kann gezeichnet werden. |
Parallele durch einen vorgegebenen Punkt
Bearbeiten
- Gegeben: Eine Gerade g1 und ein Punkt P außerhalb von g1.
Möglichkeit 1
Bearbeiten- Zeichne einen Bogen mit einem Radius r um P, welcher die Gerade g1 in einem Punkt Q schneidet.
- Trage ab Q den Radius r auf der Geraden ab (Punkt R).
- Zeichne einen Bogen mit dem Radius r um R, welcher den ersten Bogen in Punkt S schneidet.
- Die Gerade durch S und P ist die Parallele.
Möglichkeit 2
Bearbeiten
- Zeichne einen unterbrochenen Kreisbogen um den auf der Geraden g1 gewählten Punkt M durch den Punkt P mit dem Radius r1. Er schneidet die Gerade g1 in den Punkten A und B.
- Zeichne einen Kreisbogen mit dem Radius r2, entspricht dem Abstand |AP|, um den Punkt B bis er den Kreisbogen um M in C schneidet.
- Die Gerade durch P und C ist die Parallele.
Möglichkeit 3 mit kollabierendem Zirkel
Bearbeiten
- Zeichne einen Kreis um den auf der Geraden g1 gewählten Punkt M durch den Punkt P. Er schneidet die Gerade g1 im Punkt A.
- Zeichne einen Kreis um den Punkt P durch den Punkt M.
- Zeichne einen Kreis um den Punkt A durch den Punkt M. Er schneidet den Kreis um P in B.
- Die Gerade durch P und B ist die Parallele.
Weblinks
Bearbeiten
Dreieckskonstruktionen
Bearbeiten

Bezeichnungen
Bearbeiten- Angaben in kursiver Schrift dienen der Verbesserung der Genauigkeit und sind nicht zwingend notwendig.
Die fünf Standardkonstruktionen
BearbeitenKonstruktion 1 (SSS)
Bearbeiten
- Gegeben: Die drei Seiten a, b und c
- Notwendige Bedingung:Die Differenz von zwei Seiten (Betrag) muss kleiner sein als die dritte Seite (Dreiecksungleichungen).
- Trage auf einer Geraden eine der Seiten ab. Am besten die längste Seite.
- Zeichne um einen Endpunkt einen Bogen mit dem Radius, welcher einer anderen Seite entspricht.
- Zeichne um den anderen Endpunkt einen Bogen mit dem Radius, welcher der dritten Seite entspricht.
- Die beiden Schnittpunkte zeigen den dritten Eckpunkt für die beiden spiegelsymmetrischen Lösungen auf.
| Hinweis |
| Sofern auf der Zeichenfläche keine der Seiten eine gegebene Position hat, sollte mit der längsten Seite begonnen werden. Dies ermöglicht das genaueste Ergebnis. |
Konstruktion 2 (SWS)
Bearbeiten
- Gegeben: Zwei Seiten und der eingeschlossene Winkel.
- Beispiel
- Gegeben: a, b, γ
- Zeichne die Strecke AC = b
- Trage am Endpunkt C den Winkel γ an.
- Trage auf dem freien Schenkel (Gerade g) die Strecke a ab. Man erhält den dritten Eckpunkt B.
- Verbinde die Punkte A und B miteinander.
Konstruktion 3 (WSW)
Bearbeiten
Gegeben: Eine Seite und die anliegenden Winkel.
- Beispiel
- Gegeben: c, α und β
- Trage auf einer Geraden die Seite c ab.
- Trage an die Enden der Seite c auf einer Seite der Geraden die Winkel β und α an.
- Verlängere ggf. die freien Schenkel (f und g) der Winkel bis sie sich (im Punkt C) schneiden.
- Notwendige Bedingung: Die Summe der beiden Winkel ist kleiner als der gestreckte Winkel.
Konstruktion 4 (SWW)
Bearbeiten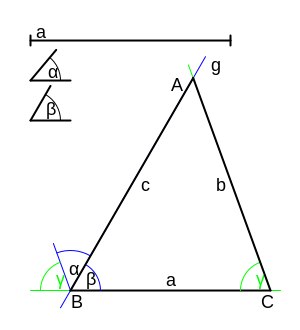
Gegeben: Eine Seite, ein anliegender und der gegenüberliegende Winkel.
- Beispiel
- gegeben: a, β und α.
- Trage auf einer Geraden die Seite a ab.
- Trage an einem Ende der Seite a (Ecke B) den Winkel β an (Gerade g).
- Trage in Punkt B an den freien Schenkel den Winkel α nach außen an. Man erhält den Winkel α + β
- Der Winkel zwischen dem so gewonnenen weiteren freien Schenkel und der Gerade, auf der sich die Seite a befindet, ist der Winkel 180° - α - β = γ.
- Trage den Winkel γ an der Ecke C an.
- Verlängere ggf. die freien Schenkel der Winkel β und γ bis sie sich (im Punkt A) schneiden.
1. Alternativ ab 4.: Verschiebe die sich durch den Winkel α ergebende Strecke von Punkt B parallel nach Punkt C. Der sich ergebende Schnittpunkt dieser Parallelen mit der Geraden g (siehe 2.) ergibt Punkt A.
2. Alternative: Über die Winkelsumme im Dreieck von 180° kann man den dritten Winkel γ = 180° - α vorab berechnen. Dann kann man das Dreieck auch nach Konstruktion 3 (WSW) konstruieren.
Konstruktion 5 (SSW)
BearbeitenGegeben: Zwei Seiten und ein anliegender Winkel.
- Beispiel
- gegeben: a, b und β.
- Trage auf einer Geraden diejenige Seite ab, an der der gegebene Winkel anliegt, im Beispiel also die Seite a.
- Trage an der Ecke B der Seite a den Winkel β an und verlängere den freien Schenkel.
- Zeichne um den anderen Endpunkt der Seite a, also um die Ecke C, einen Bogen mit dem Radius der Seite b.
- Der Schnittpunkt des Kreisbogens mit dem freien Schenkel von β liefert den dritten Eckpunkt A.
- Hinweis
- Je nachdem, wie lang die beiden Seiten sind und wie groß der Winkel ist (spitz oder stumpf), gibt es keine, eine oder zwei Lösungen. Um eine eindeutige Lösung zu bekommen, muss der Winkel der größeren Seite gegenüber liegen.
Weitere Konstruktionen
BearbeitenKonstruktion 6 (HHH)
BearbeitenGegeben: Die drei Höhen ha, hb und hc
Diese Konstruktion ist relativ umfangreich und daher auf einer eigenen Seite dargestellt. Siehe dazu unter Dreieck aus drei Höhen.
Dreieck aus drei Höhen
Bearbeiten

Dreieckskonstruktion 1. Möglichkeit
Bearbeiten
Vorüberlegung:
Aus den drei Höhen lässt sich ein Dreieck nicht so ohne weiteres konstruieren. Man kann aber folgende Vorüberlegung anstellen: Die Fläche jedes Dreiecks ist Seitenlänge x Höhe / 2 und zwar für jede Seite gleich. Deshalb besteht ein Zusammenhang zwischen Seitenlängen und Höhen.
(1)
und damit
(2)
Man kann nun in einem beliebigen Dreieck von aus auf der Seite die Höhe und auf der Seite die Höhe antragen (siehe Skizze) nach (2) als Verhältnisgleichung ist
(3) und (3a)
und damit muss nach dem Strahlensatz die Verbindungslinie parallel zu laufen.

Weiter ist dann nach dem Strahlensatz
(4)
(4a)
(3a) in (4a) eingesetzt:
(4b)
Damit sind für das Hilfsdreieck die drei Seiten bekannt und ist nach dem Kongruenzsatz SSS konstruierbar.
Die eigentliche Dreieckskonstruktion ist nun relativ einfach:
Man konstruiert das Dreieck aus den Seiten , und . Auf die Seite fällt man ein Lot zu Punkt und verlängert dieses auf die Länge . Durch den Endpunkt der Höhe zieht man eine Parallele zur Linie deren Schnittpunkte mit den Verlängerungen von und die Punkte und ergeben (siehe Skizze).
Dreieckskonstruktion 2. Möglichkeit
Bearbeiten
Teil 1: Konstruktion der Strecke d mit dem Strahlensatz
Bearbeiten- Zeichne eine Gerade und trage ab.
- Konstruiere mit dem Zirkel den Punkt in einem Abstand von und .
- Zeichne das gleichschenklige Dreieck .
- Trage auf beiden Schenkeln die Strecken ab.
- Die Strecke hat die Länge .
Teil 2: Konstruktion des Dreiecks
Bearbeiten
- Zeichne um ein Ende der Strecke (Punkt ) einen Kreisbogen mit dem Radius und um das andere Ende (Punkt ) einen Kreisbogen mit dem Radius . Es entstehen zwei zur Strecke symmetrische Schnittpunkte ( und ).
- Zeichne die Geraden und .
- Fälle das Lot von auf durch Verbinden der Punkte und .
- Trage auf dieser Lotgerade von aus die Strecke ab (Endpunkt ).
- Konstruiere zur Strecke eine parallele Gerade im Abstand .
- Ermittle dazu zuerst mit dem Zirkel den Schnittpunkt eines Bogens um mit dem Radius und eines Bogens um Punkt mit dem Radius .
- Verfahre mit einem Bogens um mit dem Radius und einem Bogen um mit dem Radius genauso.
- Verbinde die so gewonnenen Punkte mit einer Geraden.
- Die Schnittpunkte dieser Gerade mit den Geraden und bildet das gesuchte Dreieck .
Durchführbarkeit der Konstruktion
BearbeitenDie beschriebene Konstruktion ist offenbar genau dann durchführbar, wenn konstruiert werden kann. Dies ist genau dann der Fall, wenn usw. gilt, was aber laut Vorbemerkung auch notwendig ist.
Dreieckskonstruktion 3. Möglichkeit
BearbeitenIn der folgenden Konstruktion entsteht direkt aus dem sogenannten Hilfsdreieck AB1C1 das gesuchte Dreieck ABC.
Vorüberlegungen
BearbeitenNach der allgemeinen Formel für den Flächeninhalt des Dreiecks mit der Grundlinie gilt
- mit verdoppeltem Flächeninhalt gilt
- mit der Bedingung der Flächeninhalt bleibt unverändert, wird z. B. die Grundlinie verdoppelt, damit ergibt sich
- somit zeigt sich
die Länge der Grundlinie des Dreiecks verhält sich umgekehrt proportional zur Höhe .
Für das gesuchte Dreieck bedeutet dies:
- oder
- daraus folgt:
Zwei Seitenlängen eines Dreiecks verhalten sich demnach zueinander wie die Kehrwerte der entsprechenden Höhen. Dies bedeutet, ein sogenanntes Hilfsdreieck dessen Seitenlängen (direkt) proportional zu den Höhen und sind, ist ähnlich dem gesuchten Dreieck
Multipliziert man , bzw. mit dem Proportionalitätsfaktor , so erhält man für die Seitenlängen und des Hilfsdreiecks folgende Werte:
Ist die Seitenlänge , als Strecke , aus den zwei Höhen und mithilfe des 2. Strahlensatzes auf einer Geraden konstruiert, werden die Höhen und als Seiten des Hilfsdreiecks eingearbeitet. Abschließend erhält man durch eine zentrische Streckung des Hilfsdreiecks das endgültige Dreieck
Konstruktionsplan
Bearbeiten
- Bezeichne die Höhen unter Berücksichtigung, dass nicht länger als ist.
- Zeichne eine Gerade und bestimme darauf den ersten Eckpunkt des späteren Dreiecks.
- Errichte eine Senkrechte zur Gerade im Punkt und übertrage darauf die Höhe als Strecke ab.
- Konstruiere eine Parallele zur Gerade durch den Punkt
- Zeichne einen Kreisbogen um den Punkt mit dem Radius gleich der Höhe er schneidet die Gerade im Punkt
- Verbinde den Punkt mit dem Punkt
- Zeichne einen Kreisbogen um den Punkt mit dem Radius gleich der Höhe
- Errichte eine Senkrechte zur Strecke im Punkt sie erzeugt den Schnittpunkt auf dem Kreisbogen mit Radius gleich der Höhe
- Zeichne eine Parallele zur Strecke ab dem Punkt bis zur Gerade es ergibt sich der Schnittpunkt
- Zeichne einen Kreisbogen um den Punkt mit dem Radius gleich der Höhe es ergibt sich der Schnittpunkt auf dem Kreisbogen mit dem Radius gleich der Höhe somit sind die drei Eckpunkte des Hilfsdreiecks bestimmt.
- Zeichne eine Gerade ab dem Punkt durch den Punkt bis auf die Gerade es ergibt sich der Schnittpunkt Der Punkt ist der zweite Eckpunkt des späteren Dreiecks.
- Verbinde den Punkt mit dem Punkt
- Zeichne eine Parallele zur Strecke ab dem Punkt bis auf die Gerade es ergibt sich der Schnittpunkt Der Punkt ist der dritte Eckpunkt des Dreiecks.
- Verbinde den Punkt mit dem Punkt somit ist das Dreieck konstruiert.
Beweis
Bearbeiten
Seitenlängen des Hilfsdreiecks
BearbeitenFür die Seitenlängen des Hilfsdreiecks ergibt sich:
(Konstruktionsplan, 5.)
(Konstruktionsplan, 10.)
Die Dreiecke und sind zueinander ähnlich, da sie in zwei Winkeln übereinstimmen. Daraus folgt und weiter
Seitenverhältnisse im Hilfsdreieck
BearbeitenAus dem letzten Abschnitt folgt unmittelbar:
Übergang zum Dreieck
BearbeitenWegen der Parallelität von und (Punkt 13. des Konstruktionsplans) sind die Dreiecke und zueinander ähnlich. Somit erhält man für die Seitenverhältnisse im Dreieck :
Berücksichtigt man, dass die Höhen umgekehrt proportional zu den Seiten sind, so erhält man daraus:
Wegen übereinstimmender Seitenverhältnisse kann man daraus schließen, dass das konstruierte Dreieck zum gesuchten Dreieck ähnlich ist.
Da der Abstand zwischen den Geraden und gleich ist (Konstruktionsplan, 3.), hat die Höhe den richtigen Wert, das heißt das konstruierte Dreieck ist nicht nur ähnlich, sondern sogar kongruent zum gesuchten Dreieck.
Berechnung der Dreiecksseiten und des Flächeninhalts
Bearbeiten
1. Dreieck
- 1.1
2. Dreieck
- 2.1
3. Hilfsdreieck
- 3.1 Bezeichnungen:
- 3.2 Kosinussatz:
- 3.3 Folgerung:
- Durch Erweitern mit ergibt sich daraus
- .
- 3.4
- 3.5
4. Ähnliche Dreiecke:
- 4.1
5. Dreieck
- 5.1 Einsetzen des Rechenausdrucks für in die letzte Gleichung ergibt die Seitenlänge :
Entsprechend erhält man die beiden anderen Seitenlängen:
- 5.2
- 5.3
- 5.4 Der Flächeninhalt ergibt sich daraus gemäß der Formel :
Dreieckskonstruktion, 4. Möglichkeit
Bearbeiten
Nachfolgend wird eine relativ einfache Form der Konstruktion aus den drei Höhen erläutert. Diese Lösung kommt ohne jede Vorberechnung aus. Die als gewählte Höhe sollte kleiner als sein.
1. Konstruiere das gleichschenklige nach dem Kongruenzsatz SSS aus den Seitenlängen (2 mal) und
2. Trage auf den beiden Strecken jeweils die Strecke von Punkt ab. Man erhält die Punkte und
3. Die Verbindung der beiden Endpunkte und ergibt die Strecke
4. Schlage einen Kreisbogen mit dem Radius um den Punkt
5. Schlage einen weiteren Kreisbogen mit dem Radius um den Punkt
6. Der Schnittpunkt der beiden Kreisbögen ergibt den Dreieckspunkt
7. Zeichne eine parallele Strecke zu im Abstand von Punkt
8. Zeichne eine Strecke von über hinaus. Der Schnittpunkt mit der vorherigen Parallelen ergibt Punkt des gesuchten Dreiecks
9. Zeichne eine Strecke von über hinaus. Der Schnittpunkt mit der vorherigen Parallelen ergibt Punkt des gesuchten Dreiecks
10. Damit ist das konstruiert
Weblinks
Bearbeiten- Kosinussatz
- Konstruktion mit Zirkel und Lineal
- Kongruenzsatz
- Parallelogramm
- Proportionalitätsfaktor
- Strahlensatz
- Matroids Matheplanet Zum HHH-Fall ein Beispiel für eine Konstruktion, aus dem Buch "geometria – scientiae
Viereckskonstruktionen
Bearbeiten

Die Konstruktionsbeschreibungen bauen auf die Grundkonstruktionen auf. Die Reihenfolge ist so
gewählt, dass nachfolgende Beschreibungen auf die zuvor dargestellten Bezug nehmen können.
Konstruktion einer Raute
BearbeitenFall DS
Bearbeiten
- Gegeben: Eine Diagonale d und die Seite s.
- Zeichne eine Gerade und trage die Diagonale AC ab.
- Zeichne um die Streckenenden je einen Bogen mit dem Radius r gleich der Seitenlänge s.
- Die Schnittpunkte der Bögen ( B und D) sind die fehlenden Eckpunkte.
- Verbinde die Punkte A, B, C und D zyklisch miteinander.
| Hinweis |
| Dieses Verfahren ist eine Konstruktion der Mittelsenkrechten mit vorgegebenem Zirkelradius. |
Fall DD
Bearbeiten
- Gegeben: Die beiden Diagonalen.
- Zeichne eine Gerade g1 und trage die Diagonale d1 = AC ab.
- Konstruiere die Mittelsenkrechte g2 dazu.
- Trage auf der Mittelsenkrechten vom Schnittpunkt g1 x g2 mit dem Zirkel auf einer Seite die zweite Diagonale d2 ab (Punkt P).
- Halbiere diese Diagonale (Punkt B).
- Übertrage den so gefundenen Punkt auf die andere Seite der ersten Diagonale (Punkt D).
- Verbinde die Punkte A, B, C und D zyklisch miteinander.
| Hinweis |
| Bei d1 = d2 entsteht ein Quadrat. |
Fall SW
Bearbeiten
- Gegeben: Ein Winkel α und die Seite a.
- Führe eine Winkelhalbierung durch und verwende dabei als Radius der Bögen nur die Seitenlänge.
- Zeichne statt der Winkelhalbierenden die fehlenden Seiten zum vierten Eckpunkt.
Fall GP
Bearbeiten
- Gegeben: Die Gerade, auf der eine Seite (a) liegt und einer der Eckpunkte ( A) ausserhalb.
- Konstruiere die Parallele zu g1 durch den Punkt A und verwende als Radius die Seite a.
Konstruktion eines Rechtecks
BearbeitenFall SS
Bearbeiten
- Gegeben: Seite a und b.
Konstruktion 1
Bearbeiten- Zeichne eine Gerade g1
- Konstruiere eine Parallele mit gegebenem Abstand b und verwende dabei zwei Punkte (A, B) der Gerade g1 mit dem Abstand a zueinander.
- Verbinde die gefundenen Eckpunkte C und D miteinander.
Konstruktion 2
BearbeitenKonstruktion wie beim Quadrat die Konstruktion 2, jedoch mit der Besonderheit, dass b = AD ist.
Fall SD
Bearbeiten- Gegeben: Seite a und Diagonale d.
- Zeichne eine Gerade g1 und trage darauf die Diagonale d = AC ab.
- Halbiere die Diagonale. Der so gewonnene Punkt M ist die Mitte des Rechtecks.
- Zeichne einen Vollkreis von den Enden der Diagonale um Punkt M
- Zeichne um jedes Ende der Diagonale einen Bogen mit Seite a als Radius, von jedem Ende aus auf einer anderen Seite der Diagonale. Die Schnittpunkte mit dem ersten Kreis sind die Positionen der beiden anderen Eckpunkte B und D.
- Verbinde die Punkte A, B, C und D zyklisch miteinander.
| Hinweis |
| Diese Konstruktion baut auf dem Satz des Thales auf. |
Konstruktion eines Quadrats
BearbeitenFall S
Bearbeiten- Gegeben: Seite a
Konstruktion 1
BearbeitenKonstruktion wie beim Rechteck, jedoch mit der Besonderheit, dass b = a ist.
Konstruktion 2
Bearbeiten
Eine alternative Konstruktion zeigt die nebenstehende Darstellung. Der rechte Winkel wird mithilfe des Thaleskreises gefunden.
- Zeichne die Seite a = AB.
- Bestimme den Punkt M mit einem beliebigen Abstand |AM|.
- Ziehe den Thaleskreis um Punkt M mit dem Radius |AM|. Der Schnittpunkt des Thaleskreises mit der Seite a ist E.
- Ziehe eine gerade Linie von E durch M bis zum Thaleskreis. Der Schnittpunkt der geraden Linie mit dem Thaleskreis ist F.
- Nimm die Seite a in den Zirkel und schlage einen kurzen Kreisbogen um Punkt A.
- Ziehe eine gerade Linie von A durch F bis zum kurzen Kreisbogen, dabei ergeben sich der rechte Winkel EAF und der Schnittpunkt D. Die Strecke AD ist eine Seite des entstehenden Quadrates.
- Nimm die Seite a in den Zirkel und schlage jeweils einen kurzen Kreisbogen um Punkt D und um Punkt B, die beiden Kreisbögen schneiden sich in C.
- Verbinde abschließend den Punkt B mit C und den Punkt C mit D.
Konstruktion 3
Bearbeiten
Diese Konstruktion ist der zweiten ähnlich, kommt aber mit einer einzigen Zirkeleinstellung aus.
- Zeichne die Seite a = AB.
- Zeichne einen Kreisbogen c1 mit dem Radius a um Endpunkt A der Seite (mind. einen Viertelkreis).
- Zeichne einen Kreisbogen c2 mit dem Radius a um den Endpunkt B der Strecke (mind. einen Viertelkreis). Der Schnittpunkt mit c1 ist Punkt M (die dritte Ecke des gleichseitigen Dreiecks ABM).
- Zeichne eine Gerade g1 von B durch M, mind. um BM über M hinaus.
- Zeichne mit dem gleichen Radius a einen Thaleskreisct um M, von B über A bis zu g1; der Schnittpunkt ist E.
- Verbinde A mit E; der neue Schnittpunkt mit c1 ist eine weitere Ecke (D) des Quadrats.
- Zeichne mit dem gleichen Radius a um Eckpunkt D einen dritten Kreisbogen c3 von A bis zum anderen Schnittpunkt mit c2; Dieser ist die vierte Ecke C des Quadrats.
- Verbinde die Punkte B, C, D und A zum Quadrat.
Fall D
Bearbeiten
- Gegeben: Diagonale d.
- Zeichne die Diagonale d = AC.
- Halbiere die Diagonale und zeichne dabei durch die Schnittpunkte O und P die Mittelsenkrechte ein. Der so gewonnene Punkt M ist die Mitte des Quadrats.
- Zeichne einen Vollkreis von den Enden der Diagonale um Punkt M.
- Die Schnittpunkte des Kreises mit der Mittelsenkrechten sind die beiden anderen Eckpunkte B und D des Quadrats.
- Verbinde die Punkte A, B, C und D zyklisch miteinander.
Konstruktion eines Parallelogramms
BearbeitenFall SSH
Bearbeiten
- Gegeben: Die Seiten a und b und die Höhe h auf eine Seite, z. B. ha.
- Zeichne eine Gerade g1 und trage darauf die Seite a = AB ab, zu der die Höhe gegeben ist.
- Konstruiere die Parallele im Abstand ha.
- Zeichne um die Enden der Seite einen Bogen mit dem Radius gleich der anderen Seitenlänge.
- Zwei Schnittpunkte mit m Abstnd a sind die beiden fehlenden Eckpunkte C und D.
- Verbinde die Punkte A, B, C und D zyklisch miteinander.
Fall SWS
Bearbeiten- Gegeben: Beide Seiten und ein Winkel.
- Trage auf den Schenkeln des Winkels die beiden Seiten ab.
- Zeichne um die freien Enden der Seiten einen Bogen mit dem Radius gleich der jeweils anderen Seite.
- Die fehlende vierte Ecke ist derjenige Schnittpunkt der beiden Bögen, welcher zu einem konvexen Viereck führt, das andere Viereck ist überschlagen.
- Verbinde die Eckpunkte zyklisch miteinander.
| Hinweis |
| Diese Konstruktion baut auf der Dreieckkonstruktion "SWS" auf. |
Fall HWH
Bearbeiten
- Gegeben: Beide Höhen und ein Winkel.
- Konstruiere eine Gerade und eine Parallele mit einer Höhe als Abstand.
- Trage an einem Punkt der Geraden den Winkel an.
- Zeichne eine Parallele zum anderen Schenkel des Winkels im Abstand der anderen Höhe.
- Verbinde die Eckpunkte miteinander.
Konstruktion eines Drachenvierecks
Bearbeiten
Fall WSS
BearbeitenGegeben: Die beiden Seitenlängen a und b und ein zwischen gleichen Seiten (auf der Symmetrieachse) liegender Winkel α
- Zeichne eine Gerade, Wähle darauf einen Punkt A und trage von dort die Seite mit dem angrenzenden gegebenen Winkel ab.
- Trage in Punkt A den geg. Winkel an.
- Trage auf dem freien Schenkel des Winkels die andere Seite gleicher Länge ab.
- Zeichne um die beiden freien Enden (Die Ecken B und D) einen Kreis mit einem Radius gleich der anderen Seitenlänge.
- Derjenige Schnittpunkt der Kreise, welcher einen größeren Abstand zu A hat, ist die vierte Ecke C. (Der andere Schnittpunkt erzeugt ein konkaves Viereck) . Verbinde die Punkte B und D mit dem Punkt C.
Fall SWS
BearbeitenGegeben: Die beiden Seitenlängen a und b und ein zwischen verschiedenen Seiten ( nicht auf der Symetrieachse) liegender Winkel β
- Zeichne eine Gerade, Wähle darauf einen Punkt A und trage von dort die Seite mit dem angrenzenden gegebenen Winkel ab. Das andere Seitenende ist Punkt B.
- Trage in Punkt B den geg. Winkel an.
- Trage auf dem freien Schenkel des Winkels die andere Seite ab. Man erhält den Punkt C.
- Verbinde die freien Endpunkte A und C miteinander. Das ist eine Diagonale und die Symetrieachse.
- Spiegele Punkt B an dieser Diagonalen. Der Spiegelpunkt ist die vierte Ecke D.
- Verbinde D mit A und C.
Konstruktion eines Sehnenvierecks
Bearbeiten
Sonstige Vierecke
Bearbeiten
Kurzinhalt: Hier werden verschiedene Konstruktionen für regelmäßige Polygone vorgestellt. Das Kapitel Animationen stellt einige davon in einem animierten Video dar. Für Näherungskonstruktionen wird die Genauigkeit berechnet und eindrucksvoll veranschaulicht.
Polygonkonstruktionen
Bearbeiten

Einführung
BearbeitenDie Konstruktion von Polygonen hängt nicht nur von der Eckenzahl, sondern auch von den Symmetrien ab. So benötigt man z.B. für die Konstruktion eines Quadrates nur eine Größe (Länge der Seite oder Diagonale), da die große Symmetrie festschreibt, dass a) alle Winkel rechte Winkel sind und b) alle Seiten gleich lang sind. Nimmt man eine Symmetrie weg, z.B. das Rechteck, so dass sich die generelle Unbestimmtheit erhöht (Seiten können verschieden lang sein) so benötigt man bereits zwei Werte. Geht man zum Parallelogramm über (Winkel sind paarweise variabel) , so benötigt man drei Werte u.s.w. Die Zusatzbedingungen, wie z.B. gleiche Werte, sorgen dafür, dass man zusätzliche Werte als ursprünglich gegeben erhält.
Beispiel
BearbeitenBei einem Dreieck ist nur eine Seite gegeben. Das reicht im allgemeinen Fall nicht für die Konstruktion aus. ist aber noch angegeben, dass es sich um ein gleichseitiges Dreieck handelt, so kann aus den Formeln
- α + β + γ = 180°
und
- a = b = c (gleichseitig)
die Angabe
- α = β = γ = 60°
gewonnen werden. Hier ergeben sich also vier Werte, davon sind drei voneinander unabhängig. Diese Werte reichen für die Konstruktion aus.
Allgemeines Polygon
BearbeitenEin unregelmäßigen N-Eck ist konstruierbar, wenn:
- N-1 Seiten und die dazwischenliegenden N-2 Winkel bekannt sind.
Regelmäßiges Polygon
BearbeitenAnimationen
BearbeitenAlternative Konstruktionen (bei gegebenem Umkreis) zu Quadrat, Fünfeck, Achteck und Zehneck sind auf einer Extraseite zu finden.
Dreieck
BearbeitenDas "regelmäßige" Dreieck ist das gleichseitige Dreieck. Zur Konstruktion bei gegebener Seite siehe Konstruktion 1 (SSS) mit dem Sonderfall, dass alle Seiten gleich sind.
Die Konstruktion bei gegebenem Umkreis entspricht weitgehend der Konstruktion des Sechsecks, mit dem Unterschied, dass nur jeder zweite Punkt auf dem Kreis miteinander verbunden wird.
Viereck
BearbeitenDas regelmäßige Viereck ist das Quadrat. Siehe Konstruktion eines Quadrats.
Fünfeck
BearbeitenFünfeck bei gegebenem Umkreis
Bearbeiten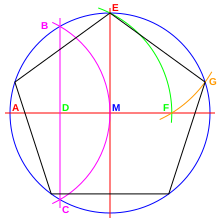
- Zeichne einen Kreis (späterer Umkreis, blau) mit Radius r um dem Mittelpunkt M.
- Zeichne zwei zueinander senkrechte Durchmesser (rot) ein.
- Halbiere einen Radius (magenta, Punkt D).
- Zeichne einen Kreis (grün) mit dem Radius DE um Punkt D. Er schneidet die Strecke AM im Punkt F. Die Strecke EF ist die Länge der Seite.
- Zum Abtragen auf dem Umkreis einen weiteren Kreisbogen (orange) mit Radius EF um E zeichnen. Er schneidet den ersten Kreis (blau) in G. Vorgang entsprechend wiederholen.
Fünfeck bei gegebener Seitenlänge
Bearbeiten
Mit Anwendung des goldenen Schnitts, äußere Teilung.
- Zeichne eine Strecke AB deren Länge die vorgegebene Seite des Fünfecks ist.
- Verlängere die Strecke ab dem Punkt A um ca. drei Viertel der Strecke AB
- Zeichne einen Kreisbogen um den Punkt B mit dem Radius AB.
- Zeichne einen Kreisbogen um den Punkt A mit dem Radius AB, es ergibt sich der Schnittpunkt F.
- Errichte eine Senkrechte zur Strecke AB durch den Punkt F, es ergibt sich der Punkt G
- Zeichne eine Parallele zur Strecke FG ab dem Punkt A bis über den Kreisbogen um Punkt A, es ergibt sich der Schnittpunkt H.
- Zeichne einen Kreisbogen um den Punkt G mit dem Radius GH bis zur Verlängerung der Strecke AB, es ergibt sich der Schnittpunkt J.
- Zeichne einen Kreisbogen um den Punkt B mit dem Radius BJ bis über die Senkrechte die durch den Punkt F geht, es ergeben sich die Schnittpunkte D auf der Senkrechten und E mit dem Kreisbogen um Punkt A.
- Zeichne einen Kreisbogen um den Punkt D mit dem Radius BA bis er den Kreisbogen um Punkt B schneidet, es ergibt sich der Schnittpunkt C.
- Verbinde die Punkte B-C-D-E-A, somit ergibt sich das Fünfeck.
Wie in der Konstruktion bei gegebenem Umkreis, ist auch hier der Goldene Schnitt der maßgebende Baustein:
Sechseck
BearbeitenSechseck bei gegebenem Umkreis
Bearbeiten
Ein reguläres Sechseck wird konstruiert, indem bei einem Kreis der Radius des Kreises sechsmal auf dem Kreisrand abgetragen wird. Die erhaltenen Punkte sind die Ecken des Sechsecks.
Sechseck bei gegebener Seitenlänge
Bearbeiten
Ein reguläres Sechseck lässt sich ebenfalls konstruieren, wenn eine vorhandene Strecke als Seitenlänge verwendet werden soll.
- Bezeichne die Endpunkte der Strecke mit A bzw. B.
- Zeichne einen Kreisbogen um den Punkt A mit dem Radius AB.
- Zeichne einen Kreisbogen um den Punkt B mit dem Radius AB, es ergibt sich der Schnittpunkt M, der Mittelpunkt vom späteren Umkreis.
- Zeichne einen Kreis um den Punkt M mit dem Radius AM, dies ist der Umkreis des späteren Sechsecks.
- Trage die Strecke AB ab dem Punkt B viermal mit dem Zirkel auf dem Umkreis ab.
- Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Sechseck ABCDEF
Siebeneck
BearbeitenNur mit Zirkel und Lineal kann das Siebeneck nicht exakt konstruiert werden. Es gibt jedoch Näherungen.
Näherung 1
Bearbeiten
Bei gegebenem Umkreis.
- Konstruiere das dem Kreis einbeschriebene gleichseitige Dreieck, indem am Kreis der Radius sechsmal abgetragen wird (Sechseck) und jeder zweite Punkt miteinander verbunden wird.
- Halbiere eine Dreieckseite, durch verbinden einer Ecke mit dem gegenüberliegenden Punkt auf dem Umkreis. Die halbe Dreieckseite ist eine Näherung für das Siebeneck.
Relativer Fehler:
- Bei einem Radius von 1 m ist die Seite 1,7 mm zu kurz.
- Als Ergänzung nebenan eine Konstruktion, die zwar vom 1. Punkt der Beschreibung etwas abweicht, aber mit deren 2. Punkt im Wesentlichen übereinstimmt. Sie bedarf deshalb keiner weiteren Erklärung.
Bei gegebener Seitenlänge.
- Das Besondere der nebenstehenden Darstellung ist: Sie zeigt alternativ die Umkehrung, nämlich wie aus einer gegebener Seite, mithilfe eines gleichseitigen Dreiecks mit zwei halbierten Seiten, eine Näherung für das Siebeneck entsteht.
Näherung 2
BearbeitenDiese sehr genaue Näherung ist wegen des Aufwands auf einer Extraseite zu finden.
Achteck
BearbeitenAchteck bei gegebenem Umkreis
Bearbeiten- Konstruiere das zum gegebenen Umkreis gehörende Quadrat, ohne jedoch seine Seiten einzuzeichnen (also nur die Ecken).
- Halbiere einen Zentriwinkel und übertrage ihn auf die anderen rechten Winkel.
- Verbinde die Ecken.
Achteck bei gegebener Seite
BearbeitenSiehe Achteck.
Neuneck
BearbeitenNur mit Zirkel und Lineal kann das regelmäßige Neuneck nicht exakt konstruiert werden. Es gibt jedoch Näherungen. Eine sehr genaue Näherung ist wegen des Aufwands auf einer Extraseite zu finden.
Zehneck
Bearbeiten- Konstruiere ein regelmäßiges Fünfeck, entsprechend der Konstruktion eines regelmäßigen Fünfecks mit Zirkel und Lineal (s.o.).
- Ziehe eine Linie von jeder Ecke des Fünfecks durch den Mittelpunkt des Kreises, der in Schritt 1 gemacht wurde, zur anderen Seite des gleichen Kreises.
- Die fünf Ecken des Fünfecks legen jede zweite Ecke des Zehnecks fest. Die verbliebenen fünf Ecken sind die Punkte, die durch Schritt 2 auf der anderen Seite des Kreises konstruiert wurden.
Elfeck
BearbeitenDas regelmäßige Elfeck ist als klassische Konstruktion mit Zirkel und Lineal nicht darstellbar. Erlaubt man jedoch ein zusätzliches Hilfsmittel für die Teilung des 90-Grad-Winkels in elf gleich große Winkel, z. B. die archimedische Spirale oder die Quadratrix des Hippias, führt dies zu einer exakten Seitenlänge des Elfecks.
Eine Exakte Konstruktion mit der Quadratrix des Hippias als zusätzliches Hilfsmittel sowie eine Näherungskonstruktion bei gegebenem Umkreis sind wegen des Platzbedarfs auf einer Extraseite zu finden.
Zwölfeck
BearbeitenFür die Konstruktion eines regelmäßigen Zwölfecks konstruiert man die Ecken des regelmäßigen Sechsecks und halbiert die Zentriwinkel.
Dreizehneck
BearbeitenNur mit Zirkel und Lineal kann das regelmäßige Dreizehneck nicht exakt konstruiert werden.
Eine Exakte Konstruktion bei gegebenem Umkreis mit Hilfsmittel sowie eine Näherung ist wegen des Platzbedarfs auf einer Extraseite zu finden.
Vierzehneck
BearbeitenNur mit Zirkel und Lineal kann das regelmäßige Vierzehneck nicht exakt konstruiert werden. Eine Exakte Konstruktion bei gegebenem Umkreis mit Hilfsmittel sowie eine Näherung ist wegen des Platzbedarfs auf einer Extraseite zu finden.
Fünfzehneck
BearbeitenDas regelmäßige Fünfzehneck ist mit Zirkel und Lineal konstruierbar. Die Konstruktionen zu "Bei gegebenem Umkreis" bzw. "Bei gegebener Seitenlänge" sind im Artikel Fünfzehneck beschrieben.
Siebzehneck
BearbeitenDas regelmäßige Siebzehneck ist mit Zirkel und Lineal konstruierbar.
Die Konstruktionen zu "Bei gegebenem Umkreis" bzw. "Bei gegebener Seitenlänge" sind auf einer Extraseite zu finden.
Eigenschaften, Mathematischer Hintergrund u. a. m. ist im Artikel Siebzehneck beschrieben.
257-Eck
BearbeitenExakte Konstruktion
Eine exakte Konstruktion mit gegebenem Umkreis ist in 257-Eck beschrieben. Ein Zitat aus dem Artikel: "Die praktische Durchführung der Konstruktion ist per Hand kaum möglich, da die Anforderungen an Präzision bei der notwendigen Größe sehr schwer einzuhalten sind."
- Näherungskonstruktion der 1. Seite
- Da die exakte Konstruktion des 257-Ecks sehr umfangreich ist und nicht übersichtlich dargestellt werden kann, macht es Sinn auch eine pragmatische Lösung darzustellen. Diese Näherung ist wegen des Aufwands auf einer Extraseite zu finden.
- Exakte Konstruktion der 1. Seite mit der Quadratrix des Hippias als zusätzliches Hilfsmittel
- Erlaubt man jedoch neben Zirkel und Lineal ein zusätzliches Hilfsmittel für die Teilung des 90-Grad-Winkels in n gleich große Winkel, z. B. die archimedische Spirale oder die Quadratrix des Hippias, ist eine gut nachvollziehbare exakte Konstruktion der ersten Ecke E1 des 257-Ecks darstellbar. Diese Konstruktion ist auf der gleichen Extraseite zu finden.
65537-Eck
Bearbeiten- Näherungskonstruktion der 1. Seite
- Im Folgenden wird die erste Seite als Näherungskonstruktion mit zwei Hauptschritten, in vergrößerter Ansicht, dargestellt. Diese Näherung ist wegen des Aufwands auf einer Extraseite zu finden.
Animationen
Bearbeiten

Quadrat
Bearbeiten- Die Vorgehensweise ergibt sich aus der Animation.
Fünfeck
Bearbeiten- Die Vorgehensweise ergibt sich aus der Animation.
Achteck
Bearbeiten- Die Vorgehensweise ergibt sich aus der Animation.
Zehneck
BearbeitenDie Konstruktion entspricht der Konstruktion der Ecken eines Fünfecks mit anschließender Winkelhalbierung.
Siebeneck
Bearbeiten

Siebeneck (Heptagon)
BearbeitenNäherungskonstruktion (!) für das regelmäßige Siebeneck, auch mit Zirkel und Lineal ohne Maßeinteilung darstellbar.
Die gepunkteten Linien mit den daraufliegenden Punkten, dienen als Hilfe für die Berechnung der Seite des Siebenecks.

Konstruktion
Bearbeiten- Zeichne um einen Punkt M einen Kreis - den späteren Umkreis des Siebenecks - mit Radius r.
- Zeichne zwei zueinander senkrechte Geraden durch den Mittelpunkt. Einer der Schnittpunkte mit dem Kreis ist die erste Ecke A des Siebenecks.
- Teile die Strecke AM in drei Teile, es ergeben sich die Punkte J und K
- Zeichne einen Halbkreis um den Mittelpunkt M mit Radius MJ, er schneidet die Strecke MH im Punkt L.
- Zeichne einen Kreisbogen um Punkt A mit Radius r ab Punkt M, er schneidet den Halbkreis im Punkt N.
- Zeichne eine Gerade ab Punkt L durch Punkt N etwas über den Umkreis hinaus.
- Errichte eine Senkrechte zur Gerade, die durch Punkt N geht, ab Punkt A bis sie den Umkreis im Punkt O schneidet, es ergibt sich der Schnittpunkt P.
- Errichte eine Senkrechte zur Strecke AM im Punkt J bis sie die Strecke AO im Punkt Q schneidet.
- Zeichne einen Kreisbogen um Punkt H mit Radius r, es ergibt sich der Schnittpunkt R auf dem Umkreis.
- Errichte eine Senkrechte zur Strecke MH durch Punkt R, sie halbiert die Strecke MH im Punkt S.
- Zeichne einen Kreisbogen um Punkt R mit Radius OQ.
- Zeichne einen Kreisbogen um Punkt S mit Radius r bis er den Kreisbogen um Punkt R schneidet, es ergibt sich der Schnittpunkt T
- Zeichne eine Gerade ab Punkt T durch Punkt Q bis zur Gerade, die durch Punkt N geht, es ergibt sich der Schnittpunkt U
- Zeichne einen Kreisbogen um Punkt A mit Radius AU ab Punkt U, er schneidet den Umkreis im Punkt B.
- Verbinde den Punkt A mit Punkt B, die rote Strecke AB ist die gesuchte Seite des Siebenecks.
- Trage die Strecke AB, ab Punkt B, fünfmal mit dem Zirkel auf dem Umkreis ab.
- Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Siebeneck ABCDEFG
Fehler
BearbeitenBei einem Umkreis mit Radius r = 1:
- Konstruierte Siebeneckseite s = 0,867767268512597... [LE]
- Soll-Siebeneckseite = ss = 2 • sin(180°/7) = 0,867767478235116... [LE]
- Absoluter Fehler = s − ss = -0,000000209722519... = -2,097...E-7 [LE]
Bei einem Umkreis mit Radius r = 10 km wäre die Abweichung der konstruierten Seite ≈ -2,1 mm
Berechnung
BearbeitenGleichschenkliges Dreieck AMN
Bearbeiten- 1.0
- Gegeben: ; ;
- 1.1 Mit dem Kosinussatz ergibt sich:
- 1.2 Höhe zur Seite
- 1.3
Rechtwinkeliges Dreieck LJN
Bearbeiten- 2.0
- Gegeben:
- (aus 1.3)
- (aus 1.2)
- 2.1
- 2.2 Hypotenuse
- Winkel ergibt sich aus
- 2.3
- 2.4
Rechtwinkeliges Dreieck LAP
Bearbeiten- 3.0
- Gegeben:
- ähnlich zu (aus 2.0)
- (aus 2.2)
- (aus 2.4)
- 3.1
- 3.2
- 3.3
- oder:
- 3.3
Rechtwinkeliges Dreieck JAQ
Bearbeiten4.0
- Gegeben:
- (aus 3.3)
- 4.1
- 4.2.
Gleichseitiges Dreieck HMR
Bearbeiten- 5.0
- Gegeben:
- 5.2 Höhe:
Rechtwinkeliges Dreieck HAO
Bearbeiten- 6.0
- Gegeben:
- ähnlich (aus 2.0) also
- (aus 4.2)
- ; ; (aus 2.4)
6.1
6.2
Stumpfwinkeliges Dreieck RST
Bearbeiten- 7.0
- Gegeben:
- (aus 6.2)
- (aus 5.2)
7.1 Nach dem Kosinussatz gilt:
7.2 Berechnung und
- (Berechnung indirekt, um den arithm. Ausdruck zu erhalten)
- Mit dem Additionstheorem:
- ergibt sich:
7.3 Höhe von zur Seite
Rechtwinkeliges Dreieck TWR
Bearbeiten- 8.0
- Gegeben:
- (aus 6.2)
- (aus 7.3)
8.1
Rechtwinkeliges Dreieck QXT
Bearbeiten9.0
- Gegeben:
- (aus 7.3)
- (aus Zeichnung)
- 9.1
- 9.2
- mit
- (aus 5.2)
- (aus 8.1)
- (aus 4.1)
- ergibt sich:
9.3 Berechnung
- mit
Rechtwinkeliges Dreieck QPU
Bearbeiten10.0
- Gegeben:
- (aus 4.2)
- (aus 3.2)
- (aus 3.1)
- (aus 9.3)
10.1
10.2 Berechnung
- Mit dem Additionstheorem
- ergibt sich:
- mit
- mit
- 10.3
-
- mit
Rechtwinkeliges Dreieck APU
Bearbeiten11.0
- Gegeben:
- (aus 3.2)
- (aus 10.3)
- 11.1
Die Länge der Siebeneckseite entspricht AU und beträgt:
- Vereinfacht:
- mit
Weblinks
Bearbeiten![]() Siebeneck, Näherungskonstruktion
Siebeneck, Näherungskonstruktion
Neuneck
Bearbeiten

Neuneck (Nonagon)
Bearbeiten- Näherungskonstruktion für das regelmäßige Neuneck, auch mit Zirkel und Lineal ohne Maßeinteilung darstellbar.
- Einleitung und Erklärungen zu "Mathematische Zusammenhänge", "Konstruktionen" mit weiteren Näherungskonstruktionen u. a. m. sind in dem Artikel Neuneck enthalten.
Konstruktion
BearbeitenBesonderheit
Bearbeiten- Die Darstellung zeigt eine Konstruktion bei gegebenem Umkreis. Eine Alternative bei gegebener Seite ist mit "alternativ" gekennzeichnet.
Konstruktion bei gegebenem Umkreis
Bearbeiten
- Zeichne eine frei wählbare Strecke MJ.
- Bestimme den Punkt S auf der Strecke MJ. In der Darstellung wurde hierfür die Strecke MJ halbiert. Prinzipiell ist die Lage des Punktes S bei gegebenem Umkreis frei wählbar.
- Zeichne um den Punkt M einen Kreis durch den Punkt S, es ist der Umkreis des späteren Neunecks.
- Ziehe einen kurzen Kreisbogen um den Punkt J mit dem Radius MJ.
- Bestimme den Punkt B mit einem Abstand |SB|, der gleich lang ist wie die Strecke MS. Dies ist der erste Eckpunkt des entstehenden Neunecks.
- Zeichne eine gerade Linie ab dem Punkt M bis zum kurzen Kreisebogen, es ergibt sich der Schnittpunkt K.
- Verbinde den Punkt K mit dem Punkt J, somit entsteht das gleichseitige Dreieck MJK.
- Konstruiere vom Winkel die Winkelhalbierende W1.
- Konstruiere vom Winkel die Winkelhalbierende W2, mit einer Länge ca. drei Viertel der Strecke MJ.
- Konstruiere vom Winkel die Winkelhalbierende W3, etwas länger als die Strecke MJ.
- Konstruiere vom Winkel die Winkelhalbierende W4, mit einer Länge etwa gleich lang wie die Winkelhalbierende W3.
- Zeichne den Kreisbogen b um den Punkt M, ab dem Punkt K bis zur Winkelhalbierende W4, es ergibt sich der Schnittpunkt O auf W4 und der Schnittpunkt N auf W3.
- Zeichne eine gerade Hilfslinie g die über den Punkt O den Punkt N anvisiert (quasi ein Lineal an die Punkte O und N angelegt), aber nur bis zum Punkt O verläuft. Somit ist zwischen den Punkten O und N keine gerade Hilfslinie g und der Kreisbogen MON für den späteren Schnittpunkt R frei zugänglich.
- Zeichne einen Halbkreis um den Punkt O mit dem Radius |NO|, es ergibt sich auf der Hilfslinie g der Schnittpunkt P.
- Konstruiere auf der Hilfslinie g die Strecke PQ, sie ist ein Drittel der Strecke OP.
- Zeichne einen Kreis um den Punkt Q mit dem Radius OP, es ergibt sich auf dem Kreisbogen MON der Schnittpunkt R.
- Verbinde den Punkt R mit dem Punkt M, es ergibt sich der Schnittpunkt A auf dem Umkreis des entstehenden Neunecks.
- Verbinde den Punkt A mit dem Punkt B, es ergibt sich die erste Seite des entstehenden Neunecks.
- Trage die Strecke AB siebenmal entgegen dem Uhrzeigersinn auf dem Umkreis ab.
- Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Neuneck ABCDEFGHI.
Fehler der ersten Seite
BearbeitenGegeben:
Beispiel zur Verdeutlichung
BearbeitenBei einem Umkreisradius r = 100.000 km wäre der absolute Fehler der 1. Seite ca. 8,6 mm.
Konstruktion bei gegebener Seite
Bearbeiten- Zeichne eine frei wählbare Strecke MJ.
- Konstruiere über und mittels der Strecke MJ ein gleichseitiges Dreieck und bezeichne den dritten Eckpunkt mit K.
- Konstruiere vom Winkel die Winkelhalbierende W1.
- Konstruiere vom Winkel die Winkelhalbierende W2, mit einer Länge ca. drei Viertel der Strecke MJ.
- Konstruiere vom Winkel die Winkelhalbierende W3, etwas länger als die Strecke MJ.
- Konstruiere vom Winkel die Winkelhalbierende W4, mit einer Länge etwa gleich lang wie die Winkelhalbierende W3.
- Zeichne den Kreisbogen b um den Punkt M, ab dem Punkt K bis zur Winkelhalbierende W4, es ergibt sich der Schnittpunkt O auf W4 und der Schnittpunkt N auf W3.
- Zeichne eine gerade Hilfslinie g die über den Punkt O den Punkt N anvisiert (quasi ein Lineal an die Punkte O und N angelegt), aber nur bis zum Punkt O verläuft. Somit ist zwischen den Punkten O und N keine gerade Hilfslinie g und der Kreisbogen MON für den späteren Schnittpunkt R frei zugänglich.
- Zeichne einen Halbkreis um den Punkt O mit dem Radius |NO|, es ergibt sich auf der Hilfslinie g der Schnittpunkt P.
- Konstruiere auf der Hilfslinie g die Strecke PQ, sie ist ein Drittel der Strecke OP.
- Zeichne einen Kreis um den Punkt Q mit dem Radius OP, es ergibt sich auf dem Kreisbogen MON der Schnittpunkt R.
- Verbinde den Punkt R mit dem Punkt M.
- Konstruiere vom Winkel die Winkelhalbierende W5.
- Zeichne auf der Winkelhalbierenden W5 einen Kreis um den in der Lage frei wählbaren Punkt T mit einem Radius, der gleich der halben gegebenen Neuneckseite ist.
- Konstruiere eine Senkrechte zur Winkelhalbierende W5 durch den Punkt T, es ergibt sich auf dem Kreis um Punkt T der Schnittpunkt V.
- Konstruiere eine Parallele zur Winkelhalbierende W5 ab dem Punkt V bis zur Strecke MK, es ergibt sich der Schnittpunkt B. Dies ist der erste Eckpunkt des entstehenden Neunecks.
- Zeichne um den Punkt M einen Kreis durch den Punkt B, es ist der Umkreis des entstehenden Neunecks. Es ergibt sich der Schnittpunkt A auf der Strecke MR.
- Verbinde den Punkt A mit dem Punkt B, dies ist die erste Seite des entstehenden Neunecks.
- Trage die Strecke AB siebenmal entgegen dem Uhrzeigersinn auf dem Umkreis ab.
- Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Neuneck ABCDEFGHI.
Fehler des Umkreisradius
BearbeitenGegeben:
Beispiel zur Verdeutlichung
BearbeitenBei einer Seitenlänge s1 = 10.000 km wäre der konstruierte Umfangsradius r ≈ 14.629,0219989 km um ca. 1,8 mm zu kurz.
Berechnung
BearbeitenKreissektor mit gleichseitigem Dreieck MJK
Bearbeiten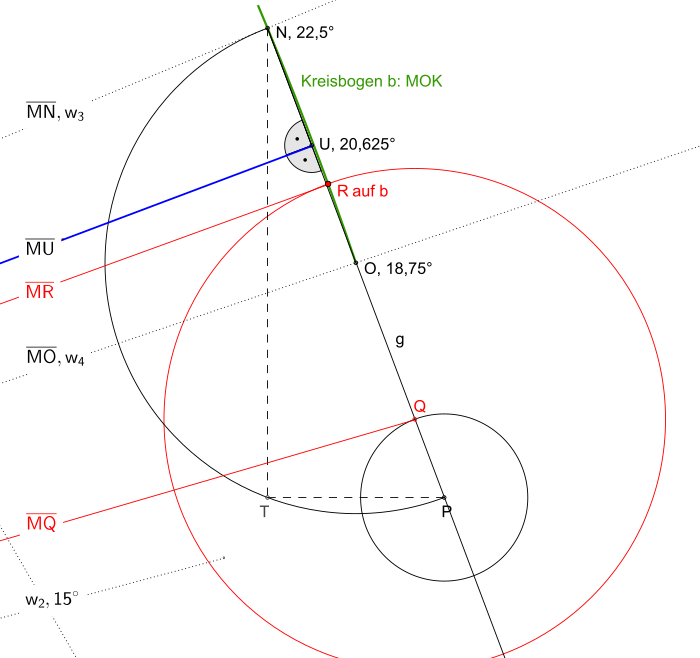
Gegeben aus Zeichnung:
Rechtwinkeliges Dreieck PNT
BearbeitenGegeben:
- Der Punkt liegt mittig auf der Sekante
Rechtwinkeliges Dreieck MNU
BearbeitenGegeben:
Rechtwinkeliges Dreieck MQU
BearbeitenGegeben:
Stumpfwinkeliges Dreieck MQR
BearbeitenGegeben:
Mit dem Kosinussatz ergibt sich:
Nebenwinkel JMR
BearbeitenGegeben:
Zentriwinkel RMK
BearbeitenGegeben:
Erste Seite des Neunecks
BearbeitenGegeben:
- 8.1
Konstruierter Umkreisradius bei gegebener Seite s1
BearbeitenGegeben:
Umkreisradius bei gegebener Seite s1
BearbeitenGegeben:
Weblinks
BearbeitenDreiteilung des Winkels 60° in diesem Buch im Kapitel Die drei antiken Probleme
Drittel der Strecke in diesem Buch im Kapitel Verschiedenes
Neuneck mit gegebener Seitenlänge
![]() Konstruktion einer Parallelen durch einen gegebenen Punkt
Konstruktion einer Parallelen durch einen gegebenen Punkt
Elfeck
Bearbeiten

Elfeck (Hendekagon)
BearbeitenDas regelmäßige Elfeck ist als klassische Konstruktion mit Zirkel und Lineal nicht darstellbar. Erlaubt man jedoch ein zusätzliches Hilfsmittel für die Teilung des 90-Grad-Winkels in elf gleich große Winkel, z. B. die archimedische Spirale oder die Quadratrix des Hippias, führt dies zu einer exakten Seitenlänge des Elfecks.
Näherungskonstruktionen hierfür sind selbstverständlich machbar, es sind aber nur wenige in der einschlägigen Literatur zu finden. Die bekanntesten ist wohl die Näherungskonstruktion nach Dürer aus dem Jahr 1525.
Exakte Konstruktion bei gegebenem Umkreis mithilfe der Quadratrix des Hippias als zusätzliches Hilfsmittel
Bearbeiten
- Zeichne einen Kreis mit dem Radius r = 1 (Einheitskreis).
- Konstruiere über dem Radius OA1 das Quadrat OA1BC.
- Bestimme die Quadratrix von Hippias mit der Parameterkurve :
mit
- Zeichne eine Halbgerade ab dem Mittelpunkt O.
- Trage auf der Halbgeraden ab O elf gleiche Abstände ab. Aus Gründen der Übersichtlichkeit sind in der Zeichnung nur die relevanten Teilungspunkte bis 4 und der Abschlußpunkt 11 dargestellt.
Anmerkung
Der Zentriwinkels des Elfecks ergibt sich aus aber die Quadratrix des Hippias unterteilt nur die Winkel ab bis in gleich große Winkel. Daraus folgt, ein Elftel der Strecke OC kann nur ein Elftel des Winkels erzielen. Deshalb wird wegen der Berechnung des Zentriwinkels aus dem Umkreis mit seinen das Vierfache eines Elftels, d. h. der Teilungspunkt der Strecke OC, zur Konstruktion des Zentriwinkels genutzt.
- Verbinde den Abschlußpunkt 11 mit C.
- Ziehe eine Parallele zu C11 ab dem Teilungspunkt 4 bis OC, damit ergibt sich der Punkt 4'.
- Ziehe eine Parallele zu OA1 ab dem Punkt 4' bis zur Quadratrix, damit ergibt sich der Punkt D.
- Ziehe eine gerade Linie vom Mittelpunkt O durch D bis zur Kreislinie, damit ergibt sich der zweite Eckpunkt A2 des entstehenden Elfecks sowie der Mittelpunktswinkel (Zentriwinkel) μ.
- Verbinde den Punkt A1 mit A2, die Länge der Strecke ist die exakte Seitenlänge des regelmäßigen Elfecks.
- Trage auf dem Umkreis ab dem Eckpunkt A2 die Strecke A1A2 neunmal gegen den Uhrzeigersinn ab und verbinde abschließend die benachbarten Eckpunkte miteinander.
Näherungskonstruktion bei gegebenem Umkreis
Bearbeiten
- Es sei ein Kreis um mit beliebigem Radius .
- Halbgerade durch und ergibt Schnittpunkt .
- Halbgerade senkrecht zu durch ergibt Schnittpunkte und .
- Strecken eintragen.
- Kreis um durch ergibt Schnittpunkte und .
- Strecke , Kreis um durch .
- Bestimmen der Funktionspunkte:
- Es beginnt mit Punkt , dessen Abstand zu Punkt ist gleich der Strecke . In der Darstellung beschrieben als . Auf diese Art und Weise werden auch die weiteren Funktionspunkte von als bis als (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.
- Einzeichnen der Kreissekanten:
- Es beginnt mit der Sekante ab durch bis sie die äußere Kreislinie in schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt durch bis sie wieder die äußere Kreislinie in schneidet. Auf diese Art und Weise werden auch die Punkte von bis (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.
- Die Verbindung von mit schneidet den innersten Kreis in als zweiten Eckpunkt des entstehenden Elfecks.
- Trage auf den Umkreis ab Eckpunkt die Strecke , sie entspricht der Seitenlänge des Elfecks, neunmal gegen den Uhrzeigersinn ab und verbinde abschließend die benachbarten Eckpunkte miteinander.
- Somit ergibt sich:
- Eine Näherung des regelmäßigen Elfecks E1 bis E11.
Ergebnis
BearbeitenBezogen auf den Einheitskreis r = 1 [LE]
- Konstruierte Seitenlänge des Elfecks in GeoGebra (Anzeige max. 15 Nachkommastellen)
- Seitenlänge des Elfecks
- Absoluter Fehler der konstruierten Seitenlänge:
- Bis zu den max. angezeigten 15 Nachkommastellen ist der absolute Fehler
- Konstruierter Zentriwinkel des Elfecks in GeoGebra (Anzeige signifikante 13 Nachkommastellen)
- Zentriwinkel des Elfecks
- Absoluter Winkelfehler vom konstruierten Zentriwinkel:
- Bis zu den angezeigten signifikanten 13 Nachkommastellen ist der absoluter Fehler
Beispiel um den Fehler zu verdeutlichen
BearbeitenBei einem Umkreisradius r = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 55 min), wäre der absolute Fehler der konstruierten Seitenlänge < 1 mm.
Bei gegebener Seitenlänge
Bearbeiten
Ist die Seitenlänge a' eines Elfecks bei gegebenem Umkreis bereits bestimmt, kann daraus mithilfe der sogenannten zentrischen Streckung ein Elfeck mit gegebener Seitenlänge a (in der nebenstehenden Zeichnung grün) konstruiert werden.
- Ist die gegebene Seitenlänge a länger als a', so verlängere zuerst beide Winkelschenkel des Zenriwinkels .
- Konstruiere die Winkelhalbierende wh des Winkels .
- Bestimme den Punkt M auf wh mit beliebiger Position.
- Zeichne eine Parallele zu a' = A1'A2' durch M.
- Ziehe einen Halbkreis um M mit Radius r = a/2, die Schnittpunkte sind E und F.
- Zeichne je eine Parallele zu wh ab E und F bis zu dem betreffenden Winkelschenkel, die Schnittpunkte sind die beiden ersten Eckpunkte A1 und A2 des gesuchten Elfecks.
- Ziehe den somit gefundenen Umkreis um O mit dem Radius ru = OA1.
- Trage auf den Umkreis, ab dem Eckpunkt A2, die Seitenlänge a neunmal gegen den Uhrzeigersinn ab und verbinde abschließend die benachbarten Eckpunkte miteinander.
Weblinks
BearbeitenNäherungskonstruktion nach Dürer (1525)
Konstruktion mit Zirkel und Lineal
Dreizehneck
Bearbeiten

Dreizehneck (Tridecagon)
Bearbeiten- Das regelmäßige Dreizehneck ist nicht als (exakte) Konstruktion mit Zirkel und Lineal darstellbar.
Konstruktion
BearbeitenExakte Konstruktion bei gegebenem Umkreis mit Hilfsmittel
BearbeitenDie folgende Darstellung ist eine Weiterführung der Konstruktionskizze nach Andrew Mattei Gleason aus dem Jahr 1988, mit dem Hilfsmittel Tomahawk zur Dreiteilung eines Winkels (siehe Weblinks).
Für das Dreizehneck beginnt man im Koordinatenursprung eines kartesischen Koordinatensystems mit einem Kreis um Punkt mit Radius . Es folgt die Festlegung des Punktes . Um den Punkt zu erhalten, werden zunächst die Zahlenwerte , als zwölfter Teil von , sowie bestimmt, die Strecke halbiert und um deren Mittelpunkt der Thaleskreis gezogen. Die danach errichtete Senkrechte auf ab schneidet den Thaleskreis in . Die Verbindung des Punktes mit ergibt für das Eintragen des Punktes . Im Anschluss die Zahlenwerte und auf ermitteln sowie die Punkte und einzeichnen.
Zum Finden der Punkte und wird zuerst der Zahlenwert auf festgelegt und eine Senkrechte durch die errichtet. Zieht man nun einen Kreisbogen um durch , schneidet er die Senkrechte in und . Nach dem Verbinden der Punkte und mit sowie dem Ziehen eines Kreises um durch , wird der Winkel mit einer frei wählbaren Methode gedrittelt. Hier z. B. geschieht dies mithilfe eines sogenannten Tomahawks, dabei ergeben sich die Punkte und . Eine Gerade durch und ergibt und , die Eckpunkte eines regelmäßigen Dreizehnecks sind. Die übrigen Eckpunkte können durch Verwendung des Kreisbogens nacheinander gefunden werden.
Näherungskonstruktion bei gegebenem Umkreis
Bearbeiten
- Es sei ein Kreis um mit beliebigem Radius .
- Gerade durch und ergibt Schnittpunkt .
- Gerade senkrecht zu durch ergibt Schnittpunkte und .
- Strecken eintragen.
- Kreis um durch ergibt Schnittpunkte und .
- Strecke , Kreis um durch .
- Bestimmen der Funktionspunkte:
- Es beginnt mit Punkt , dessen Abstand zu Punkt ist gleich der Strecke . In der Darstellung beschrieben als . Auf diese Art und Weise werden auch die weiteren Funktionspunkte von als bis als (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.
- Einzeichnen der Kreissekanten:
- Es beginnt mit der Sekante ab durch bis sie die äußere Kreislinie in schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt durch bis sie wieder die äußere Kreislinie in schneidet. Auf diese Art und Weise werden auch die Punkte von bis (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.
- Die Verbindung von mit schneidet den innersten Kreis in , als zweiten Eckpunkt des entstehenden Dreizehnecks.
- Trage auf den Umkreis ab dem Eckpunkt die Strecke , sie entspricht der Seitenlänge des Dreizehnecks, elfmal gegen den Uhrzeigersinn ab und verbinde abschließend die benachbarten Eckpunkte miteinander.
- Somit ergibt sich:
- Eine Näherung des regelmäßigen Dreizehnecks E1 bis E13.
Ergebnis
BearbeitenBezogen auf den Einheitskreis r = 1 [LE]
- Konstruierte Seitenlänge des Dreizehnecks in GeoGebra (Anzeige max. 15 Nachkommastellen)
- Seitenlänge des Dreizehnecks
- Absoluter Fehler der konstruierten Seitenlänge:
- Bis zu den max. angezeigten 15 Nachkommastellen ist der absolute Fehler
- Konstruierter Zentriwinkel des Dreizehnecks in GeoGebra (Anzeige max. 14 Nachkommastellen)
- Zentriwinkel des Dreizehnecks
- Absoluter Winkelfehler vom konstruierten Zentriwinkel:
- Bis zu den max. angezeigten 14 Nachkommastellen ist der absoluter Fehler
Beispiel um den Fehler zu verdeutlichen
BearbeitenBei einem Umkreisradius r = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 55 min), wäre der absolute Fehler der konstruierten Seitenlänge < 1 mm.
Weblinks
BearbeitenKonstruktion mit Zirkel und Lineal
Vierzehneck
Bearbeiten

Vierzehneck (Tetradecagon)
Bearbeiten- Das regelmäßige Vierzehneck ist nicht als Konstruktion mit Zirkel und Lineal darstellbar.
Konstruktion
BearbeitenExakte Konstruktion bei gegebenem Umkreis mit Hilfsmittel
BearbeitenDie folgende Darstellung ist eine Weiterführung der Konstruktionskizze (Abbildung) des Siebenecks (Heptagon) nach Andrew Mattei Gleason aus dem Jahr 1988, mit dem Hilfsmittel "Tomahawk" zur Dreiteilung eines Winkels (siehe Weblinks).
Es beginnt im Koordinatenursprung eines kartesischen Koordinatensystems im Punkt mit einem Kreis mit Radius Es folgt die Festlegung der Punkte und . Anschließend werden die Punkte und bestimmt, sie sind Eckpunkte zweier gleichseitiger Dreiecke mit Basis . Nach dem Verbinden der Punkte und mit in der Original-Zeichnung aus der Zeitschrift The American Mathematical Monthly, siehe Einzelnachweise, ist dieser Punkt zwischen und , wird um ein Kreisbogen von bis gezogen. Nun drittelt man den Winkel mit einer freiwählbaren Methode (z. B. Kurven, Tomahawk etc.), dabei ergeben sich die Punkte und . Eine Gerade durch und ergibt und , die zusammen mit Eckpunkte eines regelmäßigen Siebenecks sind.
Nun bedarf es noch einer Halbierung des Zentriwinkels des Siebenecks und man erhält so den zweiten Eckpunkt des gesuchten Vierzehnecks. Die übrigen Eckpunkte können durch Verwendung des Kreisbogens nacheinander gefunden werden.
Näherungskonstruktion bei gegebenem Umkreis
Bearbeiten
- Es sei ein Kreis um mit beliebigem Radius .
- Halbgerade durch und ergibt Schnittpunkt .
- Halbgerade senkrecht zu durch ergibt Schnittpunkte und .
- Strecken eintragen.
- Kreis um durch .
- Strecken , Kreis um durch .
- Bestimmen der Funktionspunkte:
- Es beginnt mit Punkt , dessen Abstand zu Punkt ist gleich der Strecke . In der Darstellung beschrieben als . Auf diese Art und Weise werden auch die weiteren Funktionspunkte von als bis als (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.
- Einzeichnen der Kreissekanten:
- Es beginnt mit der Sekante ab durch bis sie die äußere Kreislinie in schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt durch bis sie wieder die äußere Kreislinie in schneidet. Auf diese Art und Weise werden auch die Punkte von bis (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.
- Die Verbindung mit schneidet den innersten Kreis in als dritten Eckpunkt des entstehenden Vierzehnecks; die Strecke ist die angenäherte Seitenlänge eines regelmäßigen Siebenecks.
- Halbiere den Winkel , es ergibt auf dem innersten Kreis den Eckpunkt des Vierzehnecks.
- Verbinde den Eckpunkt mit , es ergibt die angenäherte Seitenlänge des regelmäßigen Vierzehnecks.
- Trage auf den innersten Kreis, ab dem Eckpunkt , die Seitenlänge elfmal gegen den Uhrzeigersinn ab und verbinde abschließend die benachbarten Eckpunkte miteinander.
- Somit ergibt sich:
- Eine Näherung des regelmäßigen Vierzehnecks E1 bis E14.
Ergebnis
BearbeitenBezogen auf den Einheitskreis r = 1 [LE]
- Konstruierte Seitenlänge des Vierzehnecks in GeoGebra (Anzeige max. 15 Nachkommastellen)
- Seitenlänge des Siebenecks
- Absoluter Fehler der konstruierten Seitenlänge
- Bis zu den max. angezeigten 15 Nachkommastellen ist der absolute Fehler
- Konstruierter Zentriwinkel des Siebenecks in GeoGebra (Anzeige signifikante 13 Nachkommastellen)
- Zentriwinkel des Siebenecks
- Absoluter Fehler des konstruierten Zentriwinkels
- Bis zu den angezeigten signifikanten 13 Nachkommastellen ist der absoluter Fehler
Beispiel um den Fehler zu verdeutlichen
BearbeitenBei einem Umkreisradius r = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 55 min), wäre der absolute Fehler der konstruierten Seitenlänge < 1 mm.
Weblinks
BearbeitenGleason, Andrew Mattei (March 1988). "Angle trisection, the heptagon, and the triskaidecagon p. 185–187 (p. 193 Fig.4)" Archivdatei abgerufen am 04. 04. 2016
Konstruktion mit Zirkel und Lineal
Siebzehneck
Bearbeiten

Siebzehneck
BearbeitenEigenschaften, mathematischer Hintergrund u. a. m. sind in dem Artikel Siebzehneck enthalten.
Konstruktion bei gegebenem Umkreis nach H. W. Richmond
Bearbeiten
Das folgende regelmäßiges Siebzehneck ist eine ausführlich dargestellte Version der Konstruktion, die von Herbert W. Richmond 1893 veröffentlicht wurde.
Ist ein Kreis k1 (der Umkreis um das entstehende Siebzehneck) um den Mittelpunkt O gegeben, kann das Siebzehneck konstruiert werden durch:
- Zeichnen eines Durchmessers von k1; Schnittpunkte mit k1 sind A und B.
- Konstruktion der Mittelsenkrechten m zu AB; Schnittpunkte mit k1 sind C und D.
- Konstruktion des Mittelpunktes E von DO.
- Konstruktion des Mittelpunktes F von EO und Zeichnen von FA.
- Konstruktion der Winkelhalbierenden w1 zwischen OF und FA.
- Konstruktion der Winkelhalbierenden w2 zwischen m und w1; Schnittpunkt mit AB ist G.
- Konstruktion der Senkrechten s zu w2 durch F.
- Konstruktion der Winkelhalbierenden w3 zwischen s und w2; Schnittpunkt mit AB ist H.
- Konstruktion des Thaleskreises k2 (mit Mittelpunkt M) über HA; Schnittpunkte mit CD sind J und K.
- Konstruktion eines Kreises k3 um G, der durch J und K verläuft; Schnittpunkte mit AB sind L und N (dabei liegt N sehr nahe an M).
- Konstruktion der Tangente an k3 durch N; Schnittpunkte mit k1 sind die Eckpunkte P3 und P14 des Siebzehnecks.
- Je siebenmaliges Abtragen der Sehne d1 = AP3 von k1 auf k1 – ab dem Eckpunkt P3 entgegen dem Uhrzeigersinn und ab dem Eckpunkt P14 im Uhrzeigersinn; Schnittpunkte mit k1 sind alle restlichen Eckpunkte des Siebzehnecks.
- Verbinden der so gefundenen Punkte.
Variation der Konstruktion nach H. W. Richmond
Bearbeiten
Unterschiede zum Original
- Der Kreis k2 bestimmt statt der Winkelhalbierenden w3 den Punkt H.
- Der Kreis k4 um den Punkt G′ (Spiegelung des Punktes G an m) ergibt den Punkt N, der dadurch für die Konstruktion der Tangente nicht mehr so nah an M liegt.
- Einige Bezeichnungen sind geändert.
Konstruktionsbeschreibung
- Zeichnen eines großen Kreises k1 (des Umkreises des entstehenden Siebzehnecks) um den Mittelpunkt O.
- Zeichnen eines Durchmessers; Schnittpunkte mit k1 sind A und B.
- Konstruktion der Mittelsenkrechten m zu AB; Schnittpunkte mit k1 sind C und D.
- Konstruktion des Mittelpunktes E von DO.
- Konstruktion des Mittelpunktes F von EO und Zeichnen von FB.
- Konstruktion der Winkelhalbierenden w1 zwischen OF und FB; Schnittpunkt mit AB ist Q.
- Konstruktion der Winkelhalbierenden w2 zwischen OF und FQ; Schnittpunkt mit AB ist G.
- Konstruktion von G′ durch Spiegelung von G an m.
- Konstruktion des Kreises k2 um Q, der durch F verläuft; der näher an m liegende Schnittpunkt mit AB ist H.
- Konstruktion des Thaleskreises k3 über HB; Schnittpunkte mit CD sind J und K.
- Konstruktion des Kreises k4 um G′, der durch J und K verläuft; Schnittpunkte mit AB sind L und N.
- Konstruktion der Tangente an k4 durch N; Schnittpunkte mit k1 sind die Eckpunkte P3 und P14 des Siebzehnecks.
- Je siebenmaliges Abtragen der Sehne d1 = AP3 von k1 auf k1 – ab dem Eckpunkt P3 entgegen dem Uhrzeigersinn und ab dem Eckpunkt P14 im Uhrzeigersinn; Schnittpunkte mit k1 sind alle restlichen Eckpunkte des Siebzehnecks.
- Verbinden der so gefundenen Punkte.
Gaußsche Formel für den Kosinus des Zentriwinkels als konstruierte Strecke
BearbeitenDas folgende Konstruktionsprinzip nutzt als Ansatz die gaußsche Formel für den Kosinus des Zentriwinkels
Zuerst wird auf einer Zahlengeraden der Hauptteil der Formel ohne den Faktor abgebildet. Es folgt die geometrische Division mit dem Divisor und schließt mit einer zehnfachen Vergrößerung einer Dreieckseite ab, deren Länge dem Kosinus des Zentriwinkels entspricht.
Hauptteil der Formel, ohne Faktor
Bearbeiten
- Zeichne die Zahlengerade und bestimme darauf Punkt , die Strecke und
- Errichte die Zahlengerade durch Punkt als Senkrechte zur Zahlengerade und bestimme darauf die Strecke , dabei ist Punkt auf
- Ziehe durch die zweite Zahlengerade als Parallele zur
- Halbiere die Strecke als Schnittpunkt ergibt sich Punkt
- Zeichne den Halbkreis um ab und eine Parallele zur Zahlengeraden ab Punkt bis zum Halbkreis, als Schnittpunkt ergibt sich
- Verbinde den Punkt mit , die so erhaltene Strecke
- Ziehe einen Halbkreis um Punkt mit dem Radius , als Schnittpunkt ergibt sich auf
- Übertrage ab Punkt die Strecke auf die Zahlengerade , als Schnittpunkt ergibt sich
- Zeichne eine Parallele zur Zahlengeraden ab Punkt bis , dabei ergibt sich der Schnittpunkt
- Bestimme die Strecke durch Subtraktion der Strecke von , somit ist
- Verdopple die Strecke , als Schnittpunkt ergibt sich , somit ist
- Ziehe den Kreisbogen und addiere anschließend zum Punkt die Strecke , als Schnittpunkt ergibt sich
- Errichte eine Senkrechte auf der Zahlengeraden ab Punkt bis zum Kreisbogen , als Schnittpunkt ergibt sich
- Verbinde Punkt mit , die so erhaltene Strecke
- Bestimme die Strecke durch Addition der Strecke zur Strecke , somit ist
- Fälle das Lot vom Punkt auf die Zahlengerade , als Schnittpunkt ergibt sich
- Bestimme die Strecke durch dreimalige Addition der Strecke zur Strecke , als Schnittpunkte ergeben sich und somit ist
- Bestimme die Strecke durch Subtraktion der Strecke von , somit ist
- Bestimme die Strecke sie ist gleich lang wie
- Ziehe den Kreisbogen und addiere anschließend zum Punkt die Strecke , als Schnittpunkt ergibt sich
- Errichte eine Senkrechte auf der Zahlengeraden ab bis zum Kreisbogen , als Schnittpunkt ergibt sich
- Verbinde Punkt mit , die so erhaltene Strecke
- Bestimme die Strecke durch Subtraktion der Strecke von , somit ist
- Bestimme die Strecke durch Subtraktion der Strecke von , somit ist
- Halbiere die Strecke , als Schnittpunkt ergibt sich
- Ziehe den Kreisbogen und addiere anschließend zum Punkt die Strecke , als Schnittpunkt ergibt sich
- Errichte eine Senkrechte auf der Zahlengeraden ab bis zum Kreisbogen , als Schnittpunkt ergibt sich
- Verbinde den Punkt mit , die so erhaltene Strecke
- Addiere zur Strecke zweimal die Strecke , als Schnittpunkte ergeben sich und somit ist der Hauptteil der Formel auf konstruiert; die Strecke
Geometrische Division mit dem Divisor 16
Bearbeiten
- Bestimme die Strecke durch Subtraktion der Strecke von , somit ist
- Fälle das Lot vom Punkt auf die Zahlengerade , als Schnittpunkt ergibt sich
- Zeichne eine Parallele zur Zahlengerade vom Punkt bis auf , als Schnittpunkt ergibt sich
- Halbiere die Strecke , als Schnittpunkt ergibt sich der Punkt , dabei ist auf der Zahlengeraden
- Zeichne eine Parallele zur Zahlengerade ab dem Punkt bis auf die Strecke , als Schnittpunkt ergibt sich
- Lege ein Lineal mit seiner Kante an die Punkte und danach markiere mithilfe der Linealkante auf der Zahlengeraden den Schnittpunkt Eine Linie durch nach ist nicht notwendig, sie würde auch zu dicht an der folgenden (grünen) Fuktionslinie sein.
- Verbinde den Punkt mit , die Strecke (grüne Linie) schneidet die Strecke in einem, wegen des sehr kleinen Dreiecks , nicht sichtbaren Punkt; nennen wir den virtuellen Punkt .
- Somit ist die geometrische Division mit dem Divisor durchgeführt.
- Die virtuelle Strecke entspricht bereits dem Kosinus des Zentriwinkels:
- Um das Siebzehneck fertig konstruieren zu können, bedarf es noch einer starken Vergrößerung der Strecke
Vorüberlegungen
BearbeitenBetrachtet man zuerst von den beiden ähnlichen rechtwinkligen Dreiecken und (beide nur durch deren Eckpunkte bestimmt) jeweils das Verhältnis der kleinen zur großen Kathete, so zeigt sich mit :
- d. h. bei einer Vergrößerung der kleinen Kathete mit dem Faktor wird deren Länge
Nun zum virtuellen rechtwinkligen Dreieck mit den beiden Gegebenheiten:
- Kleine Kathete ist dieselbe des rechtwinkligen Dreiecks
- Winkel am Scheitel durch den Verlauf der Strecke (grüne Linie) bestimmt.
Konstruiert man nun, wie im Folgenden beschrieben, ein rechtwinkliges Dreieck, das dem virtuellen rechtwinkligen Dreieck ähnlich ist und eine kleine Kathete mit der Länge besitzt, ergibt sich als verwendbare große Kathete nochmals der Kosinus des Zentriwinkels

Vergrößerung der Seite des virtuellen rechtwinkligen Dreiecks
Bearbeiten- Bestimme den Punkt nahe als dritten Teil der Strecke , es ergibt sich die Länge der Strecke
- Zeichne eine Parallele zur Zahlengeraden ab dem Punkt bis auf die Strecke (grüne Linie), als Schnittpunkt ergibt sich
- Zeichne ab eine Parallele zur Strecke bis auf als Schnittpunkt ergibt sich
- Das rechtwinklige Dreieck ist ähnlich dem virtuellen Dreieck der Punkt ist das Pendant des oben benannten Punktes
- Somit ist die Strecke der gesuchte Kosinus des Zentriwinkels
- Verdoppele die Strecke auf dem Zahlenstrahl und addiere anschließend dazu geometrisch den Zahlenwert (Strecke ), es ergeben sich auf die Zahlenwerte und
- Bestimme den Punkt auf beliebig und zeichne ab eine Parallele zu
- Übertrage die Strecke auf diese Parallele, als Schnittpunkt ergibt sich
- Ziehe den Umkreis des entstehenden Siebzehnecks um durch dabei ergibt sich der siebzehnte Eckpunkt .
- Übertrage die Strecke ab auf den Radius des Umkreises, als Schnittpunkt ergibt sich der Punkt
- Errichte eine Senkrechte auf ab entgegen dem Uhrzeigersinn bis zum Kreis, als Schnittpunkt ergibt sich der erste Eckpunkt des Siebzehnecks.
- Verbinde den Eckpunkt mit , somit ist die erste Seite des Siebzehnecks exakt konstruiert.
- Abschließend trage die Strecke noch fünfzehnmal gegen den Uhrzeigersinn auf den Umkreis ab. Nach dem Verbinden der benachbarten Eckpunkte ergibt sich das regelmäßige Siebzehneck .
Weblinks
BearbeitenParallele hier im Kapitel Grundkonstruktionen
Konstruktion mit Zirkel und Lineal
![]() Siebzehneck, gaußsche Formel für den Kosinus des Zentriwinkels als konstruierte Strecke, mit Kurzbeschreibung, Animation
Siebzehneck, gaußsche Formel für den Kosinus des Zentriwinkels als konstruierte Strecke, mit Kurzbeschreibung, Animation
Herbert W. Richmond 1893 Siebzehneck Beschreibung und Siebzehneck Abbildung (Fig. 6)
257-Eck
Bearbeiten


Konstruktion
BearbeitenDas regelmäßige 257-Eck, im englischen Sprachraum 257-gon, ist zwar als klassische Konstruktion mit Zirkel und Lineal theoretisch möglich, kann aber wegen der sehr hohen Anzahl und Dichte der erforderlichen Linien nicht übersichtlich abgebildet werden.
Die im Jahre 1991 veröffentlichte Konstruktionsmethode von Duane W. DeTemple unter Verwendung des sogenannten Carlyle-Kreises, ist deutlich einfacher, verwehrt aber wegen der dicht neben- und übereinander liegenden 150 Hilfskreisen den erforderlichen Durchblick.[1]
Erlaubt man jedoch neben Zirkel und Lineal ein zusätzliches Hilfsmittel für die Teilung des 90-Grad-Winkels in n gleich große Winkel, z. B. die archimedische Spirale oder die Quadratrix des Hippias, ist eine gut nachvollziehbare exakte Konstruktion der ersten Ecke E1 und damit die Seitenlänge des 257-Ecks darstellbar.
Exakte Konstruktion der Seitenlänge mit der Quadratrix des Hippias als zusätzliches Hilfsmittel
Bearbeiten
Würde der gleiche Ansatz wie beim Elfeck angewandt werden, d. h. den Umkreisradius zuerst in 257 gleiche Abschnitte teilen und anschließend den vierten Teilungspunkt zur Konstruktion des Mittelpunktswinkels μ nutzen, wäre z.B. bei einem Umkreisradius r = 100 mm der Abstand von einem zum nächsten Teilungspunkt etwas kleiner als 0,4 mm.
Eine machbare Alternative zeigt die folgende Konstruktion. Übrigens ist sie auch mit realem Zirkel, Lineal und z. B. mithilfe der Quadratrix in Form einer Schablone auf einem Blatt Papier im Format DIN A4 realisierbar.
Unter Verwendung der Quadratrix wird nicht zuerst der erste Eckpunkt E1 des 257-Ecks gesucht, sondern der sechzehnte Eckpunkt E16.
- Der Eckpunkt lässt sich auf folgende Art und Weise finden.
- Für den Mittelpunktswinkel des Kreisausschnittes gilt
- ,
- mit Berücksichtigung des Mittelpunktswinkels des Viertelkreises erhält man
- Diese Dezimalzahl ist mithilfe des dritten Strahlensatzes mit Zirkel und Lineal konstruierbar.
- Die Länge der Strecke in Längeneinheiten [LE], sprich der Abstand vom Mittelpunkt des Umkreises bis zum Funktionspunkt errechnet sich aus
- [LE]
- Der der Wert des Quotienten ist ebenso mit Zirkel und Lineal mithilfe des dritten Strahlensatzes konstruierbar.[2]
Die fünf Hauptschritte der Konstruktion
Bearbeiten- Schema
- Zahl 4,015625 (mithilfe des dritten Strahlungssatzes)
- Einheitskreis mit Quadratrix des Hippias
- Strecke OM aus dem Quotient 1 : 4,015625 (mithilfe des dritten Strahlungssatzes)
- Eckpunkt E1
Schema
Bearbeiten
- Bestimme den Punkt A.
- Zeichne die Strecke AB mit der Länge 1.
- Errichte eine zu AB senkrechte Strecke BC mit der Länge 1.
- Konstruiere eine Strecke CD parallel zur Strecke AB, etwas länger als 1.
- Zeichne eine Gerade parallel zur Strecke BC durch den Punkt A mit einer kurzen Unterbrechung nahe der Strecke CD, d. h. CD und die Gerade haben keinen Schnittpunkt.
- Teile die Strecken AB in 10 gleiche Abschnitte, aber zeichne nur die Teilungspunkte (Teilungspunkt im weiteren Verlauf mit TP bezeichnet) TP1 bis TP3 und TP5 bis TP7 ein.
- Projiziere die TPs der Strecke AB auf die Strecke CD und ergänze darauf TP4.
- Ziehe eine gerade Linie vom Punkt C durch TP1 der Strecke AB sowie eine gerade Linie vom Punkt B durch TP1 der Strecke CD, jeweils bis zur Geraden die durch A verläuft, es ergeben sich die Scheitelpunkte C1 bzw. B1.
- Verbinde TP1 von Strecke AB mit TP1 von Strecke CD, es ergibt die Strecke (1)(1).
Zahl 4,015625
Bearbeiten
- Verbinde TP5 (letzte Nachkommastelle der Zahl 4,015625) mit C1, es ergibt den Schnittpunkt 5 auf AB. Der Wert der Zahl 5 ist damit auf 0,5 verkleinert, eingetragen wird aber 5.
- Addiere 5 zum TP2 auf AB, es ergibt 25.
- Verbinde 25 mit B1, es ergibt den Schnittpunkt 25 auf CD.
- Greife die Strecke (1)25 von CD ab und subtrahiere sie vom TP7 auf AB, es ergibt 625.
- Verbinde 625 mit B1, es ergibt den Schnittpunkt 625 auf CD.
- Addiere 625 zum TP5 auf CD, es ergibt 5625.
- Zusätzlicher Hilfsstrahl wird eingearbeitet:
- Bestimme den Punkt E auf C1,B1, mit AE ungefähr ein Viertel der Länge von BC.
- Errichte eine Senkrechte zur Strecke C1,B1 ab E bis auf die Strecke (1)(1), es ergibt den Schnittpunkt F.
- Ziehe eine gerade Linie vom Punkt C durch F bis zur Strecke C1,B1, es ergibt den Schnittpunkt C2.
- Es geht weiter mit 5625
- Verbinde 5625 mit C2, es ergibt 5625 auf der Strecke EF.
- Addiere 5625 zum TP1 auf CD, es ergibt 15625.
- Verbinde 15625 mit C1, es ergibt den Schnittpunkt 15625 auf AB.
- Da die nächste Dezimalstelle eine 0 (Null) ist, muss der bisher hierher konstruierte Wert 0,15625 nochmals durch 10 geteilt werden, bevor er weiter verwendet werden kann.
- Verbinde 15625 mit B1, es ergibt den Schnittpunkt 015625 auf CD, die Unterbrechung der Geraden ermöglicht eine Markierung des Punktes 015625.
- Greife die Strecke (1)015625 von CD ab und subtrahiere sie vom TP5 auf AB, somit ist die Zahl 4,015625 fertig konstruiert.
Einheitskreis mit Quadratrix des Hippias
Bearbeiten
- Halbiere die Strecke C1,B1, es ergibt den Schnittpunkt G.
- Bestimme den Mittelpunkt O für den Umkreis des 257-Ecks mit dem Radius GO = AB = 1.
- Zeichne den Umkreis um O, es ergibt den Schnittpunkt E257 auf der Geraden.
- Errichte eine zu GE257 senkrechte Strecke OH.
- Mit den noch fehlenden Seiten (Länge 1) vervollständige das Quadrat über OE257.
- Zeichne die Quadratrix ein mit der Parameterkurve :
mit
Strecke OM aus dem Quotient 1 : 4,015625
Bearbeiten
- Verlängere die Strecke (1)(1) bis zur Strecke OH, es ergibt den Schnittpunkt I.
- Errichte eine Senkrechte im Punkt G bis zur Strecke BC, es ergibt den Schnittpunkt J.
- Ziehe eine Parallele ab der konstruierten Zahl 4,015625 bis zur Strecke GJ, es ergibt den Schnittpunkt K.
- Ziehe eine gerade Linie vom Punkt K durch I bis zur Strecke OE257, es ergibt den Schnittpunkt L.
- Verbinde Punkt J mit L, es ergibt den Schnittpunkt M auf OH, somit ist die Funktionsstrecke OM konstruiert.
Eckpunkt E16 bis E1
Bearbeiten- Ziehe eine Parallele zu OE257 ab dem Punkt M bis zur Quadratrix, es ergibt den Schnittpunkt N.
- Ziehe eine gerade Linie vom Mittelpunkt O durch N bis zur Kreislinie, damit ergibt sich der sechzehnte Eckpunkt E16 des 257-Ecks.
- Die abschließende vierfache Winkelhalbierung erzeugt die Eckpunkte , , und schließlich . Somit entspricht der Abstand |E257E1| exakt der Seitenlänge des 257-Ecks.
Näherungskonstruktion der 1. Seite
Bearbeiten
Zwar nicht exakt, aber deutlich einfacher ist die folgende Konstruktion.
- Es sei ein Kreis um mit beliebigem Radius .
- Halbgerade durch und ergibt Schnittpunkt .
- Halbgerade senkrecht zu durch ergibt Schnittpunkte und .
- Strecken eintragen.
- Kreis um durch ergibt Schnittpunkt .
- Strecke , Kreis um durch .
- Bestimmen der Funktionspunkte:
- Es beginnt mit Punkt , dessen Abstand zu Punkt ist gleich der Strecke . In der Darstellung beschrieben als . Auf diese Art und Weise werden auch die weiteren Funktionspunkte von als bis als (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.
- Einzeichnen der Kreissekanten:
- Es beginnt mit der Sekante ab durch bis sie die äußere Kreislinie in schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt durch bis sie wieder die äußere Kreislinie in schneidet. Auf diese Art und Weise werden auch die Punkte von bis (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.
- Die Verbindung von mit schneidet den innersten Kreis in , als vierten Eckpunkt des entstehenden 257-Ecks.
- Konstruiere innerhalb des Winkels zwei Winkelhalbierende, es ergeben sich die Eckpunkte und .
- Somit ergibt sich mit der Strecke annähernd die erste Seite des 257-Ecks.
Ergebnis
BearbeitenBezogen auf den Einheitskreis r = 1 [LE]
- Konstruierte Seite des 257-Ecks in GeoGebra (Anzeige 15 signifikante Nachkommastellen, gerundet)
- Seite des 257-Ecks, 15 sigifikante Nachkommastellen, ebenfalls gerundet
- Absoluter Fehler der konstruierten Seite
- Konstruierter Zentriwinkel in GeoGebra (Anzeige 14 signifikante Nachkommastellen, gerundet)
- Zentriwinkel des 257-Ecks, 14 signifikante Nachkommastellen, ebenfalls gerundet
- Absoluter Fehler des konstruierten Zentriwinkels
Beispiel um den Fehler zu verdeutlichen
BearbeitenBei einem Radius r = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 56 min) wäre der absolute Fehler der konstruierten Seitenlänge a < 1 mm.
Quellen
Bearbeiten- ↑ 257-Eck
- ↑
 257-Eck, exakte Konstruktion der 1. Seite mithilfe der Quadratrix des Hippias als zusätzliches Hilfsmittel
257-Eck, exakte Konstruktion der 1. Seite mithilfe der Quadratrix des Hippias als zusätzliches Hilfsmittel
Weblinks
BearbeitenKonstruktion mit Zirkel und Lineal
![]() 257-Eck E-15, Näherungskonstruktion der ersten Seite, Animation
257-Eck E-15, Näherungskonstruktion der ersten Seite, Animation
65537-Eck
Bearbeiten

Näherungskonstruktion der ersten Seite in zwei Hauptschritten
Bearbeiten- Da eine exakte Konstruktion allein mit Zirkel und Lineal nicht praktikabel abgebildet werden kann, wird im Folgenden mithilfe GeoGebra die erste Seite als Näherungskonstruktion in einer stark vergrößerter Ansicht dargestellt.
Näherungskonstruktion der Ecke 1.024
Bearbeiten
- Es sei ein Kreis um mit beliebigem Radius .
- Halbgerade durch und ergibt Schnittpunkt .
- Halbgerade senkrecht zu durch ergibt Schnittpunkte und .
- Strecken eintragen.
- Kreis um durch ergibt Schnittpunkt .
- Strecke , Kreis um durch .
- Bestimmen der Funktionspunkte:
- Es beginnt mit Punkt , dessen Abstand zu Punkt ist gleich der Strecke . In der Darstellung beschrieben als . Auf diese Art und Weise werden auch die weiteren Funktionspunkte von als bis als (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.
- Einzeichnen der Kreissekanten:
- Es beginnt mit der Sekante ab durch bis sie die äußere Kreislinie in schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt durch bis sie wieder die äußere Kreislinie in schneidet. Auf diese Art und Weise werden auch die Punkte von bis (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.
- Verbinde den Punkt mit dem Mittelpunkt , auf dem Umkreis ergibt sich somit annähernd die Ecke , d. h. der Kreisbogen beinhaltet annähernd 1024 Seiten des regelmäßigen 65537-Ecks.
Näherungskonstruktion der ersten Seite
BearbeitenIn der dritten Vergrößerung, ergibt sich somit annähernd die erste Seite E65537E1 = a des regelmäßigen 65537-Ecks.
Ergebnis
Bearbeiten- Konstruierter Winkel (Anzeige GeoGbra)
- Winkel , gerundet
- Absoluter Fehler des konstruierten Winkels
- (1 Winkelsekunde = = 0,000277...° = 2,77...E-4°)
- Konstruierte Seite des 65537-Ecks (Anzeige GeoGbra)
- Seite des 65537-Ecks
- Absoluter Fehler der konstruierten ersten Seite
- Absoluter Fehler der letzten Seite
- Konstruierter Zentriwinkel (Anzeige GeoGbra)
- Zentriwinkel
- Absoluter Fehler vom konstruierten Zentriwinkel
Beispiel um den Fehler zu verdeutlichen
BearbeitenBei einem Umkreisradius r = 10 Billionen km (das Licht bräuchte für diese Strecke ca. 1 Jahr und 21 Tage) wäre die 1. Seite ca. 2 mm zu kurz, bzw. die 65537. Seite ca. 131 m zu lang.
Weblinks
Bearbeiten- 65537-Eck
- GeoGebra
- Lichtgeschwindigkeit
 65527-Eck, exakte Konstruktion der 1. Seite mit der Quadratrix des Hippias und einem Programm für dynamische Geometrie als zusätzliche Hilfsmittel
65527-Eck, exakte Konstruktion der 1. Seite mit der Quadratrix des Hippias und einem Programm für dynamische Geometrie als zusätzliche Hilfsmittel- 65537-Eck aus mathematik-olympiaden.de, mit Bildern der Dokumentation nach HERMES; abgerufen am 16. Juli 2016
Kreiskonstruktionen
Bearbeiten

Konstruktion des Mittelpunkts
Bearbeiten
- Lege auf einer gegebenen Kreislinie (c0) einen Punkt (A) fest.
- Zeichne um den Punkt A einen Kreis ca mit einem Radius größer als dem des geg. Kreises, beispielsweise ca. 3/2 des gegebenen Kreises. Die Schnittpunkte mit c0 sind B und C.
- Zeichne um die Punkte B und C mit dem gleichen Radius (also durch A) zwei weitere Kreise, cb und cc. Die Schnittpunkte mit ca sind D und E, bzw. F und G.
- Verbinde die Schnittpunkte D und E, bzw. F und G jeweils mit einer Geraden. Der Schnittpunkt M ist der Mittelpunkt des gegebenen Kreises.
Konstruktion eines Kreises durch drei Punkte
Bearbeiten
Diese Konstruktion entspricht der Konstruktion des Umkreises um ein Dreieck, ohne die Dreieckseiten zu konstruieren:
- Konstruiere für die nicht notwendigerweise dargestellte Strecke zwischen zwei Punkten der gegeben Punkte A,B, und C - beispielsweise A und B - die Mittelsenkrechte. (in der Zeichnung blau).
- Verfahre mit einer anderen Strecke genauso (in der Zeichnung türkis). Der Schnittpunkt M der beiden Mittelsenkrechten ist der Mittelpunkt des gesuchten Kreises c.
- Zeichne den Kreis c durch die Punkte.
Konstruktion der Tangenten an einen Kreis
Bearbeiten
Um die Tangenten von einem Punkt P an einen Kreis C zu erhalten, verfahre wie folgt:
- Verbinde den Mittelpunkt M vom gegebenen Kreis c mit dem gegebenen Punkt P.
- Halbiere die Strecke MP; man erhält Punkt H.
- Zeichne um H einen durch M und P gehenden Kreis; Die Schnittpunkte mit dem gegeben Kreis sind die Tangentenpunkte T1 und T2.
- Zeichne die Tangenten t1 und t2.
Kurzinhalt: die Quadratur des Kreises, die Dreiteilung des Winkels, die Verdoppelung des Würfels
Näherung 1
Bearbeiten

Transformation Quadrat in Kreis
Bearbeiten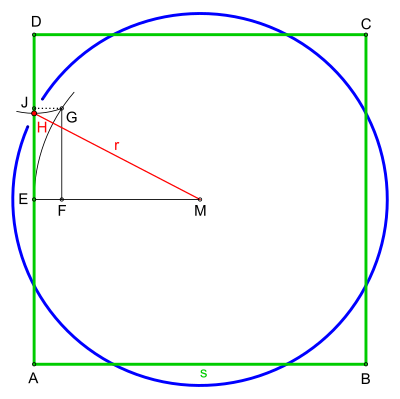
Näherungskonstruktion: Aus einem gegebenen Quadrat wird ein Kreis mit nahezu gleichem Flächeninhalt konstruiert, auch mit Zirkel und Lineal ohne Maßeinteilung darstellbar.
Die gepunktete Linie ab Punkt G sowie der Punkt J, dienen als Hilfe für die Berechnung des Radius r.
Konstruktion
Bearbeiten- Konstruiere ein Quadrat ABCD, dessen halbe Seitenlänge gleich EM ist.
- Bestimme die Strecke EF, sie ist ein Sechstel der Strecke EM.
- Zeichne einen Kreisbogen um den Mittelpunkt M mit dem Radius EM ab E.
- Errichte eine Senkrechte auf EM in F bis sie den Kreisbogen um M in G schneidet.
- Zeichne einen Kreisbogen um D mit dem Radius |DG| ab G bis er die Strecke AD in H schneidet.
- Verbinde den Punkt H mit M; die Strecke HM ist der gesuchte Radius r.
- Zeichne abschließend einen Kreis um den Mittelpunkt M mit dem Radius r.
Fehler
BearbeitenBei einem Quadrat mit der Seite s = 1 [LE]:
- Konstruierter Radius r = 0,564189924824387...[LE]
- Soll-Radius rs = = 0,564189583547756...[LE]
- Absoluter Fehler = r - rs = 0,000000341276631... = 3,412...E-7 [LE]
- Mit konstruiertem Radius r erzeugte Kreisfläche A = r2 ⋅ = 1,000001209794523... [FE]
- Soll-Kreisfläche As = 1,0 [FE]
- Absoluter Fehler = A - As = 0,000001209794523... = 1,209...E-6 [FE]
- Bei einem Quadrat mit der Seite s = 10 km wäre der Fehler des Radius r ≈ 3,4 mm
- Bei einem Quadrat mit der Seite s = 1 m wäre der Fehler der Kreisfläche A ≈ 1,2 mm2
Berechnung
BearbeitenDie gepunktete Linie ab Punkt G sowie der Punkt J, dienen als Hilfe für die Berechnung des Radius r.
Rechtwinkeliges Dreieck FMG
Bearbeiten(nicht eingezeichnet)
- Gegeben:
Rechtwinkeliges Dreieck JGD
Bearbeiten(nicht eingezeichnet)
- Gegeben:
Rechtwinkeliges Dreieck EMH
Bearbeiten(nicht eingezeichnet)
- Gegeben:
Konstruierter Radius des Kreises
BearbeitenSchema für die Näherungskonstruktion regelmäßiger Vielecke
Bearbeiten
Verwendungszweck: Als Hilfsmittel für regelmäßige Vielecke mit gegebenem Umkreis, die keine exakte Lösung haben.
Konstruktionsprinzip
Bearbeiten- Eine Anwendung des dritten Strahlensatzes in Kombination mit Zahlenstrahlen.
- Die Hauptelemente sind zwei zueinander parallele Teilerstrahlen s1 und s4, ein auf s1 senkrecht stehender Zahlenstrahl s2 und ein zu s2 paralleler Scheitelstrahl s3.
- Es sind echte und unechte Brüche sowie Dezimalbrüche, die im Schema Platz finden, einsetzbar.
- Tipp: Auf einem Ausdruck der Basiskonstruktion die entsprechende Konstruktion manuell mit Schreibstift, Zirkel und Lineal fortsetzen.
Konstruktion
Bearbeiten- Zeichne durch den Punkt M einen Kreis - den späteren Umkreis des Vielecks - mit Radius r.
- Zeichne zwei zueinander senkrechte Mittelachsen des Kreises. Der unten liegende Schnittpunkt (Mittelachse mit dem Umkreis) ist die erste Ecke A des Vielecks.
- Zeichne eine Parallele s1 zur Strecke MA durch den Punkt K.
- Zeichne eine Parallele s2 zur Strecke MK durch den Punkt A, es ergibt sich der Schnittpunkt L.
- Teile die Strecke MA in drei Teile, es ergibt sich der Schnittpunkt r/3.
- Trage die Länge r/3, vom Punkt K wegführend, ab Punkt L zweimal auf die Parallele s1 ab, es ergeben sich die Schnittpunkte N und O.
- Zeichne eine Parallele s3 zur Parallele s2 durch den Punkt O.
- Setze den Punkt P, mit dem Abstand Strecke KO + Strecke MK (oder mit einem ähnlich großen Abstand) zum Punkt O auf die Parallele s3.
- Zeichne eine Parallele s4 zur Parallele s1 durch den Punkt P ca. gleich lang wie die Parallele s1.
- Trage die Strecke L r/3, einmal ab Punkt r/3 und fünfmal ab Punkt K auf der Parallele s1 ab, es ergibt sich als zehnter Teilungspunkt der Schnittpunkt Q. Die Parallele s1 wird im Folgenden als Teilerstrahl s1 bezeichnet.
- Trage die Strecke L r/3, ab Punkt P, zehnmal auf der Parallele s4 ab, es ergibt sich als zehnter Teilungspunkt der Schnittpunkt S. Die Parallele s4 wird im Folgenden als Teilerstrahl s4 bezeichnet.
- Verbinde den Punkt N mit dem Punkt R, es ergibt sich der Schnittpunkt V.
- Zeichne eine Gerade ab dem Punkt S durch den Punkt N bis auf die Parallele s3, es ergibt sich der Schnittpunkt T. Der Punkt T ist der Scheitelpunkt für die Strahlen, die vom Teilerstrahl s4 ausgehen.
- Zeichne eine Gerade ab dem Punkt Q durch den Punkt R bis auf die Parallele s3, es ergibt sich der Schnittpunkt U. Der Punkt U ist der Scheitelpunkt für die Strahlen, die vom Teilerstrahl s1 ausgehen.
- Verbinde den Punkt L mit dem Punkt V, somit ist das Schema konstruiert.
Regelmäßige Vielecke mit gegebener Seite
BearbeitenOhne Umkreis und ohne die beiden Mittelachsen ist das Schema auch für regelmäßige Vielecke mit gegebener Seite, die keine exakte Lösung haben, anwendbar.
Siehe hierzu die Beschreibung im Abschnitt "Das regelmäßige Neuneck" unter "Regelmäßiges Neuneck mit gegebener Seite".
Weblinks
Bearbeiten Dritter Strahlensatz
Zahlenstrahl
Neuneck (Nonagon)
BearbeitenNäherungskonstruktion mit gegebenem Umkreis
Konstruktionsprinzip
Bearbeiten- Die Hauptelemente sind zwei zueinander parallele Teilerstrahlen s1 und s4, ein auf s1 senkrecht stehender Zahlenstrahl s2 und ein zu s2 paralleler Scheitelstrahl s3.
- Von dem vorgegebenen Zähler werden die Dezimalstellen in der Reihenfolge Einer, Zehner, Hunderter u. s. w. jeweils mittels Projektion mit dem Faktor bzw. falls die nächste Dezimalstelle eine "0" ist, mit dem Faktor verkleinert und auf einem Teilerstrahl s1 oder s4 geometrisch addiert oder subtrahiert.
- Ansatz: Ein Bruch der die gewünschte Näherung an 2 ⋅ sin(180°/9) hat, sowie die Anwendung des dritten Strahlensatzes in kompakter Form.
Konstruktion
Bearbeiten
- Als Basiskonstruktion ist das Schema für die Näherungskonstruktion regelmäßiger Vielecke eingearbeitet.
- Alternative: Die Konstruktion manuell mit Zirkel und Lineal auf einem Ausdruck der Basiskonstruktion erstellen.
- Wähle einen Dezimalbruch der die gewünschte Näherung an 2 ⋅ sin(180°/9) hat.
- Die Qualität der Näherung ist einfach voraussehbar, wenn ein Dezimalbruch (Anzahl der Nullen im Nenner) eingesetzt wird.
- Im dargestellten Beispiel ist der Dezimalbruch 68404/1E+5 = 684040/1E+6 = gewählt.
- Sechs Nachkommastellen sind gleich dem Wert 2 ⋅ sin(180°/9) = 0,684040286651337...
- Verbinde den vierten Punkt des Zahlenstrahls s4 (Zahl 4, Einerstelle des Zählers vom Dezimalbruch) mit dem Scheitelpunkt T, es ergibt sich der Punkt 4 auf dem Zahlenstrahl s1. Der Wert der Zahl 4 vom Zahlenstrahl s4 ist dadurch verkleinert (Faktor 1/10).
- Beachte: Die nächste Stelle (Zehner) des Zählers ist eine Null (0), deshalb muss der Wert der Zahl 4 vom Zahlenstrahl s4, vor der geometrischen Addition mit der nächsten Dezimalstelle 4, mit dem Faktor 1/100 verkleinert sein!
- Verbinde den Punkt 4 des Zahlenstrahls s1 mit dem Scheitelpunkt U, es ergibt sich der Punkt 04. Der Wert der Zahl 4 vom Zahlenstrahl s4 ist nun mit Faktor 1/100 verkleinert.
- Greife die Strecke R04 ab und subtrahiere sie vom fünften Teilungspunkt des Zahlenstrahls s1, es ergibt sich der Punkt 404. Da der Wert 404 sehr nahe am vierten Teilungspunkt liegt, wird dieser vor der geometrischen Subtraktion entfernt.
- Verbinde den Punkt 404 des Zahlenstrahls s1 mit dem Scheitelpunkt U, es ergibt sich der Punkt 404 auf dem Zahlenstrahl s4.
- Greife die Strecke P404 ab und addiere sie zum achten Teilungspunkt des Zahlestrahls s4, es ergibt sich der Punkt 8404.
- Verbinde den Punkt 8404 des Zahlenstrahls s4 mit dem Scheitelpunkt T, es ergibt sich der Punkt 8404 auf dem Zahlenstrahl s1.
- Greife die Strecke O8404 ab und addiere sie zum sechsten Teilungspunkt des Zahlestrahls s4, es ergibt sich der Punkt 68404.
- Verbinde den Punkt 68404 des Zahlenstrahls s4 mit dem Scheitelpunkt T, es ergibt sich der Punkt 68404 auf dem Zahlenstrahl s1.
- Greife die Strecke O68404 ab und addiere sie zum ersten Teilungspunkt N des Zahlestrahls s1, es ergibt sich der Punkt W.
- Zeichne eine Parallele zur Strecke LV durch den Punkt W bis zur Strecke NR, es ergibt sich der Schnittpunkt X. Die rote Strecke NX ist die Seite des Neunecks.
- Trage die Strecke NX, ab Punkt A, achtmal mit dem Zirkel auf dem Umkreis ab.
- Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Neuneck ABCDEFGHJ.
Fehler
BearbeitenBei einem Umkreisradius r = 1 [LE]:
- Konstruierte Neuneckseite s = 0,68404 [LE]
- Soll-Neuneckseite ss = 2 ⋅ sin(180°/9) ⋅ 1 [LE] = 0,684040286651337... [LE]
- Absoluter Fehler = s − ss = -0,000000286651337... = -2.866...E-7 [LE]
- Bei einem Umkreisradius r = 10 km wäre die Abweichung ≈ -2,9 mm
Berechnung
Bearbeitena) Für das dargestellte Beispiel: Konstruierte Neuneckseite
b) Allgemein: Konstruierte Neuneckseite Neuneckseite ( = Umkreisradius)
- Die Berechnung der konstruierten Neuneckseite geschieht, aufgrund des Konstruktionsprinzips, schrittweise durch die geometrischen Additionen / Subtraktionen der einzelnen Zwischenergebnissen auf den Zahlenstrahlen bzw. .
- Der vorgegebene Dezimalbruch und somit die konstruierte Seite des Neunecks werden auf der Strecke prinzipiell exakt dargestellt.
Die Quadratur des Kreises
BearbeitenNäherungskonstruktion: Aus einem gegebenen Kreis wird ein Quadrat mit nahezu gleichem Flächeninhalt sowie der halbe Kreisumfang konstruiert, auch mit Zirkel und Lineal ohne Maßeinteilung darstellbar.
Version 1, halber Kreisumfang (π) als Strecke
Bearbeiten
- Zeichne zwei zueinander senkrechte Mittelachsen des Kreises.
- Zeichne einen Kreis um den Mittelpunkt M, es ergeben sich die Schnittpunkte F und G auf den Mittelachsen.
- Errichte eine Senkrechte zur Strecke MG durch den Punkt G und eine Senkrechte zur Strecke MF durch den Punkt F, die Senkrechten schneiden sich im Punkt H.
- Konstruiere die Strecke GJ, sie ist ein Drittel der Strecke GH.
- Halbiere die Strecke GJ, es ergibt sich der Punkt K.
- Übertrage die Strecke GK auf die Strecke MG, es ergibt sich der Punkt L.
- Zeichne eine Parallele zur Strecke GH ab dem Punkt L etwas länger als die Strecke GJ.
- Übertrage die Strecke GK auf die Parallele aus 7., es ergibt sich der Punkt N.
- Übertrage die Strecke GJ auf die Parallele aus 7., es ergibt sich der Punkt O.
- Verbinde den Punkt K mit dem Punkt O.
- Verbinde den Punkt N mit dem Punkt H, es ergibt sich der Schnittpunkt P.
- Zeichne einen Kreisbogen mit dem Radius GK um den Punkt F, er schneidet die Strecke FH im Punkt Q, den Kreis im Punkt R und die Strecke FM im Punkt S.
- Errichte eine Senkrechte zur Strecke FM durch den Punkt S und eine Parallele zur Strecke FM durch den Punkt R, es ergibt sich der Schnittpunkt T.
- Verbinde den Punkt H mit dem Punkt T.
- Zeichne eine Parallele zur Strecke HT durch den Punkt P bis zur Strecke Strecke NO, es ergibt sich der Schnittpunkt U auf dem Kreis und der Schnittpunkt V auf der Strecke NO.
- Verbinde den Punkt V mit dem Punkt M. Die Strecke MV ist die halbe Seitenlänge bzw. der Inkreisradius des gesuchten Quadrates.
- Zeichne einen Kreisbogen ab dem Punkt V bis auf die Strecke MG, es ergibt sich der Schnittpunkt W.
- Übertrage die Strecke MW zweimal auf die Mittelachse MF und einmal auf die Mittelachse MG, es ergeben sich die Schnittpunkte X, Z, u. Y.
- Konstruiere das Quadrat ABCD. Die Punkte W, X, Y u. Z sind Mittelpunkte der betreffenden Seiten des Quadrates.
Halber Kreisumfang (π) als Strecke
- Errichte eine Senkrechte auf die Strecke FM im Punkt F.
- Zeichne einen Kreisbogen um den Punkt M mit dem Radius AB (s), es ergibt sich der Schnittpunkt F1.
- Verbinde den Punkt F1 mit dem Punkt M.
- Verlängere die Strecke FM mit einer Geraden ab dem Punkt F.
- Errichte eine Senkrechte auf die Strecke MF1 im Punkt F1, es ergibt sich der Schnittpunkt B1 mit der Geraden aus 23..
Die Strecke entspricht .
Fehler
BearbeitenBei einem Kreis mit Radius r = 1 [LE]:
- Konstruierte Seite des Quadrates s = 1,77245384141934376... [LE]
- Soll-Seite des Quadrates ss = = 1,772453850905516... [LE]
- Absoluter Fehler = s - ss = -0,000000009486172... = -9,486...E-9 [LE]
- Fläche des konstruierten Quadrates A = s2 = 3,141592619962188... [FE]
- Soll-Fläche des Quadrates As = = 3,141592653589793... [FE]
- Absoluter Fehler = A - As = -0,000000033627605... = -3,3627...E-8 [FE]
- Fazit: Sieben Nachkommastellen sind gleich denen von bzw. sind gleich denen von .
- Bei einem Kreis mit dem Radius r = 1000 km wäre der Fehler der Seite s ≈ -9,5 mm
- Bei einem Kreis mit dem Radius r = 10 m wäre der Fehler der Fläche A ≈ -3,4 mm2
- Bei einem Kreis mit dem Radius r = 100 km wäre der Fehler des halben Kreisumfanges U/2 ≈ -3,4 mm
Berechnung
BearbeitenDie gepunkteten schwarzen Linien sowie die Punkte A1, B1, C1, D1 und E1 dienen als Hilfe für die Berechnung der Seite des Quadrates s.
Rechtwinkeliges Dreieck A1HN
Bearbeiten
- Gegeben aus Zeichnung:

Stumpfwinkeliges Dreieck HKP (2.0) mit eingebundenem rechtwinkeligen Dreieck B1PH (2.1)
Bearbeiten
- Gegeben:
- Gegeben:

- 2.1.1
- Berechnung des arithm. Ausdrucks
- Mit dem Additionstheorem
- ergibt sich:
- 2.1.2
- Mit dem Additionstheorem
- ergibt sich:
- 2.1.3

- Berechnung des arithm. Ausdrucks
- Mit dem Additionstheorem
- ergibt sich:
- 2.2.1
- 2.2.2
- Mit dem Sinussatz ergibt sich:
- 2.3.1
Gleichschenkeliges Dreieck MFR
Bearbeiten
- Gegeben aus Zeichnung:
- Mit dem Kosinussatz ergibt sich:
- 3.1.1
- 3.1.2
- 3.2.1
Rechtwinkeliges Dreieck HE1T
Bearbeiten
- Gegeben:
Rechtwinkeliges Dreieck A1HN
Bearbeiten
- Gegeben:
Stumpfwinkeliges Dreieck E1HN
Bearbeiten
- Gegeben:
Stumpfwinkeliges Dreieck NPV
Bearbeiten
- Gegeben:
Rechtwinkeliges Dreieck LMV
Bearbeiten
- Gegeben:
- Hypotenuse
Konstruierte Seite des Quadrates
BearbeitenVersion 2
BearbeitenNäherungskonstruktion
Bearbeiten
- Kreis um mit beliebigem Radius .
- Gerade durch und ergibt Schnittpunkt .
- Gerade senkrecht zu durch ergibt Schnittpunkte und .
- Strecken eintragen.
- Kreis um durch .
- Strecken , Kreis um durch ergibt Schnittpunkt .
- Bestimmen der Funktionspunkte:
- Es beginnt mit Punkt , dessen Abstand zu Punkt ist gleich der Strecke . In der Darstellung beschrieben als . Auf diese Art und Weise werden auch die weiteren Funktionspunkte von als bis als (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.
- Einzeichnen der Kreissekanten:
- Es beginnt mit der Sekante ab durch bis sie die äußere Kreislinie in schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt durch bis sie wieder die äußere Kreislinie in schneidet. Auf diese Art und Weise werden auch die Punkte von bis (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.
- Die letzte Sekante schneidet die Strecke in und liefert somit die Strecke .
- Konstruiere abschließend mittels der Strecke das Quadrat mit Seite .
- Somit ergibt sich:
- Ein Quadrat mit einem nahezu gleichen Flächeninhalt wie der des gegebenen Kreises.
Fehler
BearbeitenBezogen auf den Einheitskreis r = 1 [LE]
Der absolute Fehler der konstruierten Seite des gesuchten Quadrats ist mit der vorliegenden Konstruktion in GeoGebra nicht darstellbar, da das Ergebnis der konstruierten Seite in allen angezeigten fünfzehn Nachkommastellen mit dem Ergebnis der berechneten Seite übereinstimmt (siehe Weblinks → GeoGebra) .
- Konstruierte Seitenlänge des Quadrates mit z. B. . → Die letzte Nachkommastelle kann sich von Konstruktion zu Konstruktion unterscheiden!
- Seitenlänge des Quadrates .
- Absoluter Fehler der konstruierten Seitenlänge:
- Bis zu den max. angezeigten 15 Nachkommastellen ist der absolute Fehler
- Flächeninhalt des konstruierten Quadrates .
- Flächeninhalt des Quadrates
- Absoluter Fehler des Flächeninhalts des Quadrates .
Beispiele um die Fehler zu verdeutlichen
Bearbeiten- Bei einem Radius r = 1 Mrd.km (das Licht bräuchte für diese Strecke ca. 56 min) wäre der Fehler der konstruierten Seite des Quadrats < 1 mm.
- Bei einem Radius r = 1.000 km wäre der Fehler des Flächeninhalts des Quadrats < -1 cm2.
Weblinks
BearbeitenDreiteilung des Winkels 60°
Bearbeiten
- Näherungskonstruktion
- "Konstruktionsprinzip", "Konstruktion Winkel 0 > bis 180°" u. a. m. siehe Kapitel Dreiteilung des Winkels.
- Beginnt der Kreisbogen b um den Punkt M ab dem Punkt E und endet im Punkt B, ist der Punkt G auf der Hilfslinie g gut erkennbar. Somit kann bereits ein Winkel 60° direkt gedrittelt werden.
Konstruktion
Bearbeiten- Zeichne durch den Punkt M eine Gerade.
- Bestimme den beliebigen Punkt A auf dieser Gerade, es ergibt sich die Strecke MA als erster Winkelschenkel.
- Konstruiere den Winkel 60° um den Punkt M entgegen dem Uhrzeigersinn, mittels je einem kurzen Kreisbogen um den Punkt A sowie um den Punkt M mit dem Radius gleich der Strecke MA, die beiden Kreisbogen schneiden sich im Punkt B
- Verbinde den Punkt M mit dem Punkt B, es ergibt sich der zweite Winkelschenkel.
- Konstruiere vom Winkel die Winkelhalbierende W1.
- Konstruiere vom Winkel die Winkelhalbierende W2, die Länge der Strecke MW2 etwas länger als
- Konstruiere vom Winkel die Winkelhalbierende W3, etwas länger als die Strecke MA.
- Konstruiere vom Winkel die Winkelhalbierende W4, etwa gleich lang wie die Winkelhalbierende W3.
- Zeichne den Kreisbogen b um den Punkt M, ab dem Punkt B bis zur Winkelhalbierende W4, es ergibt sich der Schnittpunkt E auf W4 und der Schnittpunkt D auf W3.
- Zeichne eine gerade Hilfslinie g die über den Punkt E den Punkt D anvisiert (quasi ein Lineal an die Punkte E und D angelegt), aber nur bis zum Punkt E verläuft. Somit ist zwischen den Punkten E und D keine gerade Hilfslinie g und der Kreisbogen MED für den späteren Schnittpunkt H frei zugänglich.
- Zeichne einen Halbkreis um den Punkt E mit dem Radius gleich dem Abstand |DE|, es ergibt sich auf der Hilfslinie g der Schnittpunkt F.
- Konstruiere auf der Hilfslinie g die Strecke FG, sie ist ein Drittel der Strecke EF.
- Zeichne einen Kreis um den Punkt G mit dem Radius gleich der Strecke EF, es ergibt sich auf dem Kreisbogen MED der Schnittpunkt H.
- Verbinde den Punkt H mit dem Punkt M, die Winkelschenkel MH und MA schließen den Winkel ein.
- Somit ist der Winkel 60° nahezu gedrittelt.
Zusätzliche Approximationen herleitbar
Bearbeiten- Neuneckseite
- Seite vom 36-Eck, Näherungskonstruktion Winkel 10°
- Näherungskonstruktion Winkel 5°
Fehler
Bearbeiten- Die Fehler der Winkel bzw. sind zu gering für eine korrekte Anzeige in GeoGebra, sie werden deshalb als exakt 20° bzw. 40° angezeigt.
- Neuneckseite, bei einem Radius r = MA = 100.000 km wäre der Fehler an der Sehne ca. 8,6 mm.
Berechnung
Bearbeiten- Im Kapitel Neuneck, unter Berechnung sind zur Verifizierung des Konstruktionsprinzips alle Berechnungsschritte für die Dreiteilung des Winkels 60° aufgezeigt.
Weblinks
BearbeitenNeuneck in diesem Buch im Kapitel Polynomkonstruktionen
Dreiteilung des Winkels in diesem Buch im Kapitel Die drei antiken Probleme
Dreiteilung des Winkels in diesem Buch im Kapitel Die drei antiken Probleme
Drittel der Strecke in diesem Buch
Verdoppelung des Würfels
BearbeitenVersion 1
Bearbeiten

- Quadrat mit beliebiger Seitenlänge , Ecken gegen den Uhrzeigersinn und .
- Mittelpunkt des Quadrates mithilfe zweier kurzer Diagonalenabschnitte, Umkreis des Quadrates.
- Mittelachse durch ergibt Schnittpunkte und .
- Mittelachse senkrecht zu durch ergibt Schnittpunkte und .
- Strecken .
- Strecken , Kreis um durch ergibt Schnittpunkt .
- Bestimmen der Funktionspunkte:
- Es beginnt mit Punkt , dessen Abstand zu Punkt ist gleich der Strecke . In der Darstellung beschrieben als . Auf diese Art und Weise werden auch die weiteren Funktionspunkte von als bis als (Reihenfolge siehe Kurzbeschreibung in der Darstellung) festgelegt.
- Einzeichnen der Kreissekanten:
- Es beginnt mit der Sekante ab durch bis sie die äußere Kreislinie in schneidet. Die nächste Sekante läuft ab dem zuletzt erhaltenen Schnittpunkt durch bis sie wieder die äußere Kreislinie in schneidet. Auf diese Art und Weise werden auch die Punkte von bis (Reihenfolge ist anhand des Verlaufs der Sekanten zu entnehmen) bestimmt.
- Letzte Sekante von bis schneidet die Mittelachse in .
- Ein kurzer Kreisbogen um mit Radius liefert mit die Seitenlänge des gesuchten Würfels 2.
- Somit ergibt sich:
- a) Die Strecke P1Q1, sie entspricht der Seitenlänge a2 des Würfels 2.
- b) Ein Würfel 2 mit einem Volumen, das im Vergleich zum gegebenen Würfel 1 nahezu doppelt so groß ist.
Fehler
BearbeitenBezogen auf einem Würfel mit der Seitenlänge a1 = 1 [LE]
- Konstruierte Seitenlänge des verdoppelten Würfels in GeoGebra
- Seitenlänge des verdoppelten Würfels
- Absoluter Fehler der konstruierten Seitenlänge des verdoppelten Würfels
- Volumen des verdoppelten Würfels mit konstruierter Seitenlänge in GeoGebra
- Volumen des verdoppelten Würfels
- Absoluter Fehler des Volumens mit konstruierter Seitenlänge
Beispiel um den Fehler zu verdeutlichen
Bearbeiten- Bei einem Würfel 1 mit der Seitenlänge a1 = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 55 min) wäre der Fehler der konstruierten Seitenlänge a2 des verdoppelten Würfels 2 ca. -1,2 mm.
- Bei einem Würfel 1 mit der Seitenlänge a1 = 10 km wäre der Fehler des Volumens vom verdoppelten Würfels 2 ca. -5,5 dm3 oder ca. -5,5 Liter
Version 2
BearbeitenKonstruktionsprinzip
Bearbeiten- Näherungskonstruktion
- Die Hauptelemente sind ein Zahlenstrahl s1, zwei darauf senkrecht stehende Teilerstrahlen s2 und s4, ein zu s1 paralleler Scheitelstrahl s3, zwei Diagonalstrahlen s5 und s6 und zwei Hilfsstrahlen s7 und s8. Näheres wird in der Konstruktion beschrieben.
- Von dem vorgegebenen Zähler bzw. Nenner (wenn keine Dezimalzahl) werden die Dezimalstellen in der Reihenfolge Einer, Zehner, Hunderter u. s. w. jeweils mittels Projektion mit dem Faktor bzw. falls die nächste Dezimalstelle eine "0" ist, mit dem Faktor verkleinert und auf einem Teilerstrahl s2 oder s4 geometrisch addiert oder subtrahiert.
- Zuerst wird der Nenner konstruiert, anschließend zum Punkt A des Teilerstrahls s2 addiert und der sich dabei ergebende Schnittpunkt, z. B. T, Nenner, mit dem Punkt U des Zahlenstrahls s1 (S1 Würfel 1) verbunden, dabei ergibt sich die Verbindungsstrecke T, NennerU.
- Der konstruierte Zähler wird ebenfalls zum Punkt A des Teilerstrahls s2 addiert, dabei ergibt sich der Schnittpunkt, z. B. V, Zähler.
- Die abschließende Parallele zur Verbindungstrecke T, NennerU erzeugt den Schnittpunkt W auf dem Zahlenstrahl s1. Somit entspricht die Länge der Stecke AW exakt dem Wert des vorgegebenen Bruches.
- Ansatz: Ein Bruch der die gewünschte Näherung an hat. Die Anwendung der Strahlensätze in kompakter Form.
Konstruktion
Bearbeiten- Als Basiskonstruktion ist das Schema für die Konstruktion von Brüchen auf einen Strahl eingearbeitet.
- Alternative: Auf einem Ausdruck der Basiskonstruktion die Konstruktion manuell mit Schreibstift, Zirkel und Lineal fortsetzen.
- Wähle z. B. einen Dezimalbruch der die gewünschte Näherung an hat. Die Qualität der Näherung ist einfach voraussehbar, wenn ein Dezimalbruch (Anzahl der Nullen im Nenner) eingesetzt wird.
- Im dargestellten Beispiel ist der Dezimalbruch gewählt.
- Einundzwanzig Nachkommastellen sind gleich deren des Wertes .
Nenner
Bearbeiten
- Bestimme die Seite des Würfel 1 S1 mittels der beliebigen Strecke AU.
- Konstruiere den Würfel 1 so, dass die Vorderseite auf dem Zahlenstrahl s1 und an dem Teilerstrahl s2 anliegt.
- Verbinde den Punkt T,Nenner mit dem Punkt U, somit ist der Nenner konstruiert.
Zähler
Bearbeiten- Verbinde den siebten Punkt des Teilerstrahls s4 (Zahl 7, Einerstelle des Zählers vom Dezimalbruch) mit dem Scheitelpunkt N, es ergibt sich der Schnittpunkt 7 auf dem Hilfsstrahl s7. Der Wert der Zahl 7 vom Teilerstrahl s4 ist dadurch mit dem Faktor verkleinert.
- Greife die Strecke J7 ab und addiere sie zum sechsten Teilungspunkt des Teilerstrahls s2, es ergibt sich der Schnittpunkt 67.
- Verbinde den Schnittpunkt 67 des Teilerstrahls s2 mit dem Scheitelpunkt P, es ergibt sich der Schnittpunkt 67 auf dem Hilfsstrahl s8. Es könnte alternativ mit den Scheitelpunkten O oder I verbunden werden. Damit aber die projizierten Zahlen (Schnittpunkte) zueinander einen gut erkennbaren Zwischenraum für das Abgreifen des Abstandes zum Scheitelstrahl s3 haben, ist es vorteilhaft abfangs die Teilerstrahlen (s2, s4) und Hilfsstrahlen (s7, s8) in etwa gleichmäßig zu verwenden.
- Greife die Strecke K67 ab und addiere sie zum siebten Teilungspunkt des Teilerstrahls s4, es ergibt sich der Schnittpunkt 767.
- Verbinde den Schnittpunkt 767 des Zahlenstrahls s4 mit dem Scheitelpunkt H, es ergibt sich der Schnittpunkt 767 auf dem Teilerstrahl s2.
- Greife die Strecke C767 ab und addiere sie zum vierten Teilungspunkt des Teilerstrahls s2, es ergibt sich der Schnittpunkt 4.767. Es ist bezüglich Übersicht im Folgenden vorteilhaft: Die Zifferngruppierung (Punkt oder Abstand) zu verwenden und ggf. lange Zahlen mittig mit "..." abzukürzen.
- Setze diese Vorgehensweise bis zur Zahl 49.894.873.164.767 (angezeigt als 49.894...767 auf Teilerstrahl s4) fort.
- Beachte: Die nächste Stelle des Zählers ist eine Null (0), deshalb muss der Wert der Zahl 49.894...767 vom Teilerstrahl s4, vor der geometrischen Addition mit der übernächsten Dezimalstelle 1, mit dem Faktor verkleinert sein! In diesem Fall ist die erste Verkleinerung mit dem Faktor stets auf einem Teilerstrahl durchzuführen, da die auf einem Hilfsstrahl projizierten Zahlen nicht auf den benachbarten Hilfsstrahl und nicht auf die Teilerstrahlen projiziert werden können!
- Verbinde den Schnittpunkt 49.894...767 des Teilerstrahls s4 mit dem Scheitelpunkt H, es ergibt sich der Schnittpunkt 49.894...767 auf dem Teilerstrahl s2. Der Wert der Zahl 49.894...767 vom Teilerstrahl s4 ist nun mit dem Faktor verkleinert.
- Verbinde den Schnittpunkt 49.894...767 des Teilerstrahls s2 mit dem Scheitelpunkt I, es ergibt sich der Schnittpunkt 049.894...164.767 auf dem Teilerstrahl s4. Der Wert der Zahl 49.894...767 vom Teilerstrahl s4 ist nun mit dem Faktor verkleinert.
- Greife die Strecke F049.894...164.767 ab und subtrahiere sie vom zweiten Teilungspunkt A des Teilerstrahls s2, es ergibt sich der Schnittpunkt 1.049...767.
- Setze diese Vorgehensweise fort bis der Zähler mit dem Schnittpunkt 1.259.921.049.894.873.164.767 auf dem Teilerstrahl s4 konstruiert ist.
- Greife die Strecke E1.259.921.049.894.873.164.767 ab und addiere sie zum zweiten Teilungspunkt A des Teilerstrahls s2, es ergibt sich der Punkt V, Zähler.
- Zeichne eine Parallele zur Strecke T,NennerU ab dem Punkt V, Zähler bis zum Zahlenstrahl s1, es ergibt sich der Schnittpunkt W. Die Strecke AW ist die gesuchte Seite S2 des Würfel 2.
- Konstruiere den Würfel 2 so, dass die Vorderseite auf dem Zahlenstrahl s1 und an dem Teilerstrahl s2 anliegt.
- Somit ergibt sich:
- Ein Würfel 2 mit einem Volumen, das im Vergleich zum gegebenen Würfel 1 nahezu doppelt so groß ist..
Berechnung
Bearbeiten- Allgemein: Seite des Würfel 2 S2 = S1 • .
- Die Berechnung der konstruierten Seite des Würfel 2 S2 geschieht, aufgrund des Konstruktionsprinzips, schrittweise durch die geometrischen Additionen bzw. Subtraktionen der einzelnen Zwischenergebnisse auf den Teilerstrahlen s2 bzw. s4.
- Der vorgegebene Dezimalbruch wird auf dem Teilerstrahl s4 und s2 prinzipiell exakt dargestellt.
Fehler
BearbeitenBezüglich des Ansatzes sind die Fehler bis zur 21. Nachkommastelle prinzipiell = 0 [LE bzw. VE]. Siehe hierzu auch die Abschnitte Berechnung und Weblinks (Animation).
Beispiele um den Fehler zu verdeutlichen
Bearbeiten- Bei einem Würfel 1 mit S1 = 1 Billiarde km (das Licht bräuchte für diese Strecke ca. 105,8 Jahre) wäre vom Würfel 2 der Fehler der Seite S2 ≈ -0,21 mm.
- Bei einem Würfel 1 mit S1 = 100 km wäre vom Würfel 2 der Fehler des Volumens ≈ -1,0 cm3
Weblinks
BearbeitenWeblinks
Bearbeiten
Näherung 2
Bearbeiten

Als Die drei antiken Probleme oder Klassische Probleme der antiken Mathematik werden bezeichnet:
- die Quadratur des Kreises
- die Dreiteilung des Winkels
- die Verdoppelung des Würfels
Sie sind erwiesenermaßen nicht (exakt) als Konstruktion mit Zirkel und Lineal lösbar.
- Lösungskriterien, Historisches u. a. m. sind im Artikel Klassische Probleme der antiken Mathematik enthalten.
- In diesem Kapitel werden zu den drei klassischen Problemen Methoden aufgezeigt, mit denen außergewöhnlich genaue Näherungslösungen möglich sind. Die Approximationen sind auch mit Zirkel und Lineal ohne Maßeinteilung auf Format DIN A4 darstellbar.
Hilfsmittel
BearbeitenSchema für die Konstruktion von Brüchen auf einen Strahl
BearbeitenVerwendungszweck
Bearbeiten- Für Quadratur des Kreises, Verdoppelung des Würfels u. a. m., in denen ein Bruch als exakte Strecke benötigt wird.
- Vorzugsweise geeignet für Brüche > >
Konstruktionsprinzip
Bearbeiten- Eine Anwendung des dritten Strahlensatzes in Kombination mit Zahlenstrahlen.
- Die Hauptelemente sind ein Zahlenstrahl s1, zwei darauf senkrecht stehende Teilerstrahlen s2 und s4, ein zu s1 paralleler Scheitelstrahl s3, zwei Diagonalstrahlen s5 und s6 und zwei Hilfsstrahlen s7 und s8.
- Es sind echte und unechte Brüche sowie Dezimalbrüche, die im Schema Platz finden, einsetzbar.
- Tipp: Auf einem Ausdruck der Basiskonstruktion die entsprechende Konstruktion manuell mit Schreibstift, Zirkel und Lineal fortsetzen.
Konstruktion
Bearbeiten
- Die Lage des Zahlenstrahls s1 ist frei wählbar (siehe im Folgenden Quadratur des Kreises). Ist es bezüglich des Platzbedarfs möglich, zeichne z. B. durch den Punkt A den Zahlenstrahl s1. Er ist für die Darstellung des konstruierten Zählers und des konstruierten Nenners bestimmt.
- Zeichne den Teilerstrahl s2 durch den Punkt A senkrecht stehend zum Zahlenstrahl s1.
- Trage z. B. zwei gleichlange Strecken ab dem Punkt A nach unten auf dem Teilerstrahl s2 ab und bezeichne deren Endpunkte mit B bzw. C.
- Beachte: Die Position des Punktes A vom Strahl s1 auf dem Strahl s2 (Abstand zu Punkt C) ist frei wählbar.
- Zeichne durch den Punkt C den zum Zahlenstrahl s1 parallelen Scheitelstrahl s3.
- Trage die Strecke AB achtmal ab dem Punkt A nach oben auf dem Teilerstrahl s2 ab, es ergibt sich der Schnittpunkt D,10, der Teilerstrahl s2 ist somit in zehn gleiche Teile geteilt.
- Konstruiere die Strecke CE auf dem Scheitelstrahl s3 mittels eines Kreisbogens um C mit dem Radius gleich der Strecke CD,10.
- Zeichne den Teilerstrahl s4 ab dem Punkt E parallel zum Teilerstrahl s2.
- Trage die Strecke AB einmal ab dem Punkt E sowie achtmal ab dem Punkt 2 auf dem Teilerstrahl s4 ab, es ergeben sich die Schnittpunkte F und 10,G, der Teilerstrahl s4 ist somit in zehn gleiche Teile geteilt.
- Verbinde den Punkt B mit dem Punkt F.
- Zeichne einen zum größten Teil unterbrochenen Diagonalstrahl s5 ab dem Scheitelstrahl s3 durch den Punkt B bis zum Punkt 10,G, es ergibt sich auf dem Scheitelstrahl s3 der Scheitelpunkt H. Der Scheitelpunkt H ist für die Projektionsstrahlen bestimmt, die bei der Konstruktion des Zählers bzw. Nenners vom Teilerstrahl s4 ausgehen.
- Zeichne einen zum größten Teil unterbrochenen Diagonalstrahl s6 ab dem Scheitelstrahl s3 durch den Punkt F bis zum Punkt D,10, es ergibt sich auf dem Scheitelstrahl s3 der Scheitelpunkt I. Der Scheitelpunkt I ist für die Projektionsstrahlen bestimmt, die bei der Konstruktion des Zählers bzw. Nenners vom Teilerstrahl s2 ausgehen.
- Teile den Scheitelstrahl s3 in drei gleichlange Teile, es ergeben sich die Punkte J und K.
- Zeichne die Hilfsstrahlen s7 und s8 jeweils senkrecht stehend zum Scheitelstrahl s3 ab dem Punkt J bzw. ab dem Punkt K. Die beiden Hilfsstrahlen werden alternativ nur zur Lagebestimmung (Abstand zum Scheitelstrahl s3) der projizierten Zahl verwendet.
- Beachte: Die auf einem Hilfsstrahl projizierten Zahlen können nicht auf den benachbarten Hilfsstrahl und nicht auf die Teilerstrahlen projiziert werden!
- Konstruiere die Strecke LE gleich der Strecke EI auf dem Scheitelstrahl s3
- Verbinde den Punkt L mit dem Punkt 3 auf dem Teilerstrahl s4.
- Zeichne eine Parallele zur Strecke L3 ab dem Punkt F vom Teilerstrahl s4, es ergibt sich der Schnittpunkt M auf dem Scheitelstrahl s3.
- Konstruiere die Strecke NJ gleich der Strecke LM sowie die Strecke JO gleich der Strecke EM auf dem Scheitelstrahl s3, es entstehen die beiden Scheitelpunkte N und O.
- Konstruiere die Strecke KP gleich der Strecke LM sowie die Strecke KQ gleich der Strecke EM auf dem Scheitelstrahl s3, es entstehen die beiden Scheitelpunkte P und Q.
- Somit ist das Schema (exakt) konstruiert.
Weblinks
Bearbeiten Dritter Strahlensatz
Zahlenstrahl
Quadratur des Kreises
BearbeitenVariante 1
BearbeitenNäherungskonstruktion mit Darstellung des halben Kreisumfangs
Konstruktionsprinzip
Bearbeiten- Die Hauptelemente sind ein Zahlenstrahl s1, zwei darauf senkrecht stehende Teilerstrahlen s2 und s4, ein zu s1 paralleler Scheitelstrahl s3, zwei Diagonalstrahlen s5 und s6 und zwei Hilfsstrahlen s7 und s8.
- Von dem vorgegebenen Nenner und Zähler werden die Dezimalstellen in der Reihenfolge Einer, Zehner, Hunderter u. s. w. jeweils mittels Projektion mit dem Faktor bzw. falls die nächste Dezimalstelle eine "0" ist, mit dem Faktor verkleinert und auf einem Teilerstrahl s2 oder s4 geometrisch addiert bzw. subtrahiert.
- Zuerst wird der Nenner konstruiert, anschließend zum Punkt A des Teilerstrahls s2 addiert und der sich dabei ergebende Schnittpunkt, z. B. V, Nenner, mit dem Punkt T des Zahlenstrahls s1 (Wert = 1) verbunden, dabei ergibt sich die Verbindungsstrecke V, NennerT.
- Der konstruierte Zähler wird ebenfalls zum Punkt A des Teilerstrahls s2 addiert, dabei ergibt sich der Schnittpunkt, z. B. W, Zähler.
- Die abschließende Parallele zur Verbindungstrecke V, NennerT erzeugt den Schnittpunkt B1 auf dem Zahlenstrahl s1. Somit entspricht die Länge der Stecke AB1 exakt dem Wert des vorgegebenen Bruches.
- Ansatz: Ein Bruch der die gewünschte Näherung an bzw. an hat. Die Anwendung der Strahlensätze in kompakter Form.
- Es sind sämtliche Brüche z. B. mit einer beliebigen Näherung an bzw. an einsetzbar.
Konstruktion
Bearbeiten- Als Basiskonstruktion ist das Schema für die Konstruktion von Brüchen auf einen Strahl eingearbeitet. Da für den Zahlenstrahl s1 der Abstand AC auf s2 frei wählbar ist, wurde er aus Gründen des Platzbedarfs (Einer des Zählers ist 2 ) nahe 2,5 gewählt.
- Wähle z. B. einen Dezimalbruch oder einen unechten Bruch der die gewünschte Näherung an hat.
- Im dargestellten Beispiel ist der unechte Bruch gewählt, dieser wurde schon 1770 von Johann Heinrich Lambert in seinem Buch "Beyträge zum Gebrauche der Mathematik und deren Anwendung" veröffentlicht.
- Fünfzehn Nachkommastellen sind gleich deren des Wertes .
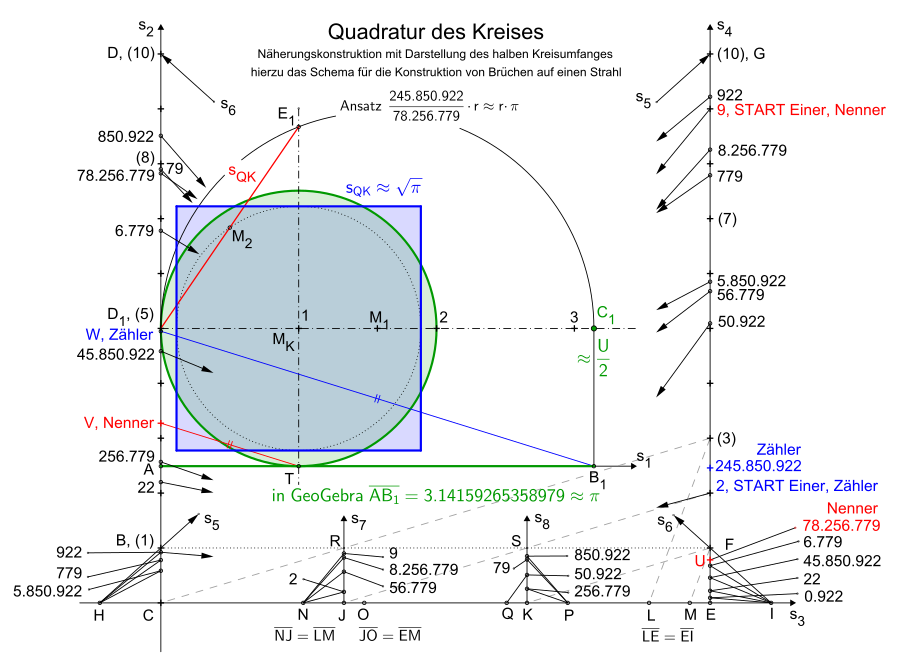
Radius des Kreises
Bearbeiten- Bestimme den Radius r des Kreises mittels der beliebigen Strecke AT. Um die prinzipielle Genauigkeit des Konstruktionsprinzips (mithilfe GeoGebra) zu verdeutlichen, ist in der folgenden Darstellung der Radius r = 1 gewählt.
- Konstruiere den Mittelpunkt MK so, dass der anschließend eingezeichnete Kreis mit dem Radius r gleich der Strecke MKT, den Teilerstrahl s2 und den Zahlenstrahl s1 berührt.
Nenner
Bearbeiten- Verbinde den neunten Punkt des Teilerstrahls s4 (Zahl 9, START Einer, Nenner) mit dem Scheitelpunkt N des Hilfsstrahls s7, es ergibt sich darauf der Schnittpunkt 9. Der Wert der Zahl 9 vom Teilerstrahl s4 ist dadurch mit dem Faktor verkleinert.
- Greife die Strecke J9 ab und addiere sie zum siebten Teilungspunkt des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt 79.
- Verbinde den Schnittpunkt 79 des Teilerstrahls s2 mit dem Scheitelpunkt P des Hilfsstrahls s8, es ergibt sich darauf der Schnittpunkt 79. Es könnte alternativ mit dem Scheitelpunkt O des Hilfsstrahls s7 oder mit dem Scheitelpunkt I des Teilerstrahls s4 verbunden werden. Damit aber die projizierten Zahlen (Schnittpunkte) zueinander einen gut erkennbaren Zwischenraum für das Abgreifen des Abstandes zum Scheitelstrahl s3 haben, ist es vorteilhaft anfangs die Teilerstrahlen (s2, s4) und Hilfsstrahlen (s7, s8) in etwa gleichmäßig zu verwenden.
- Greife die Strecke K79 vom Hilfsstrahl s8 ab und addiere sie zum siebten Teilungspunkt des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 779.
- Verbinde den Schnittpunkt 779 des Teilerstrahls s4 mit dem Scheitelpunkt H des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt 779.
- Setze diese Vorgehensweise, zuerst Projizieren, dann Abgreifen und schließlich Addieren, fort bis der Nenner mit dem Schnittpunkt 78.256.779 auf dem Teilerstrahl s4 konstruiert ist.
- Greife die Strecke EU (Nenner) ab und addiere sie zum Punkt A des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt V, Nenner. Somit ist der Nenner konstruiert.
- Verbinde den Schnittpunkt V, Nenner mit dem Punkt T des Zahlenstrahles s1, es ergibt sich die Strecke V, NennerT.
Zähler
Bearbeiten- Verbinde den zweiten Punkt des Teilerstrahls s4 (Zahl 2, START Einer, Zähler) mit dem Scheitelpunkt N des Hilfsstrahls s7, es ergibt sich darauf der Schnittpunkt 2.
- Greife die Strecke R2 ab (größere Zirkelöffnung) und subtrahiere sie vom dritten Teilungspunkt des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt 22.
- Verbinde den Schnittpunkt 22 des Teilerstrahls s2 mit dem Scheitelpunkt I des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 22.
- Greife die Strecke F22 ab und subtrahiere sie vom zehnten Teilungspunkt des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 922.
- Beachte: Die nächste Stelle des Zählers ist eine Null (0), deshalb muss der Wert der Zahl 922 vom Teilerstrahl s4, vor der geometrischen Addition mit der übernächsten Dezimalstelle 5, mit dem Faktor verkleinert sein! In diesem Fall ist die erste Verkleinerung mit dem Faktor stets auf einem Teilerstrahl durchzuführen, da die auf einem Hilfsstrahl projizierten Zahlen nicht auf den benachbarten Hilfsstrahl und nicht auf die Teilerstrahlen projiziert werden können!
- Verbinde den Schnittunkt 922 des Teilerstrahls s4 mit dem Scheitelpunkt H des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt 922.
- Verbinde den Schnittunkt 922 des Teilerstrahls s2 mit dem Scheitelpunkt I des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 0.922. Der Wert der Zahl 922 vom Teilerstrahl s4 ist dadurch mit dem Faktor verkleinert.
- Greife die Strecke F0.922 ab (größere Zirkelöffnung) und subtrahiere sie vom sechsten Teilungspunkt des Teilerstrahls s4, es ergibt sich darauf der Schnittpunkt 50.922.
- Verbinde den Schnittpunkt 50.922 des Teilerstrahls s4 mit dem Scheitelpunkt Q des Hilfsstrahls s8, es ergibt sich darauf der Schnittpunkt 50.922. Es könnte alternativ mit dem Scheitelpunkt N des Hilfsstrahls s7 oder mit dem Scheitelpunkt H des Teilerstrahls s2 verbunden werden. Damit aber die projizierten Zahlen (Schnittpunkte) zueinander einen gut erkennbaren Zwischenraum für das Abgreifen des Abstandes zum Scheitelstrahl s3 haben, ist es vorteilhaft anfangs die Teilerstrahlen (s2, s4) und Hilfsstrahlen (s7, s8) in etwa gleichmäßig zu verwenden.
- Greife die Strecke K50.922 vom Hilfsstrahl s8 ab und addiere sie zum achten Teilungspunkt des Teilerstrahls s2, es ergibt sich der Schnittpunkt 850.922.
- Setze diese Vorgehensweise, zuerst Projizieren, dann Abgreifen und schließlich Addieren, fort bis der Zähler mit dem Schnittpunkt 245.850.922 auf dem Teilerstrahl s4 konstruiert ist.
- Greife die Strecke E245.850.922 (Zähler) und addiere sie zum Punkt A des Teilerstrahls s2, es ergibt sich darauf der Schnittpunkt W, Zähler. Somit ist der Zähler konstruiert.
- Ziehe eine Parallele zur Strecke V, NennerT bis auf den Zahlenstrahl s1, damit ergibt sich der Schnittpunkt B1.
- Errichte eine Senkrechte auf den Zahlenstrahl s1 ab dem Punkt B1 bis auf die Mittelachse des Kreises, es ergibt sich der Schnittpunkt C1.
- Halbiere die Strecke D1C1, dabei entsteht der Mittelpunkt M1.
- Zeichne über M1 den Thaleskreis ab C1, er schneidet die Mittelachse des Kreises in E1.
- Verbinde den Punkt D1 mit dem Punkt E1, die Strecke D1E1 entspricht der konstruierten Seitenlänge SQK des gesuchten Quadrates.
- Halbiere die Strecke D1E1, es ergibt sich der Schnittpunkt M2.
- Zeichne einen Kreis um den Mittelpunkt MK mit dem Radius MKM2.
- Konstruiere mithilfe der Seitenlänge SQK um den Mittelpunkt MK und mittels des Hilfskreises mit dem Radius MKM2 das gesuchte Quadrat.
- Somit ergibt sich:
- a) Ein Quadrat mit einem nahezu gleichen Flächeninhalt wie der vom gegebenen Kreis.
- b) Eine Strecke AB1 mit einer Länge, die nahezu gleich dem halben Umfang des Kreises ist.
Berechnung
Bearbeiten- Allgemein: Seite des Quadrates SQ = r •
- Die Berechnung der konstruierten Seite des Quadrates SQK geschieht, aufgrund des Konstruktionsprinzips, schrittweise durch die geometrischen Additionen bzw. Subtraktionen der einzelnen Zwischenergebnisse auf den Teilerstrahlen s2 bzw. s4.
- Der vorgegebene unechte Bruch wird auf dem Zahlenstrahl s1 prinzipiell exakt dargestellt.
Absoluter Fehler der konstruierten Seitenlänge des Quadrates FSQK
Bearbeiten[LE]
Beispiele um die Fehler zu verdeutlichen
Bearbeiten- Bei einem Kreis mit Radius r = 100 Milliarden km (das Licht bräuchte für diese Strecke ca. 91 Stunden) wäre der Fehler der konstruierten Seitenlänge des Quadrates SQK ≈ 2,2 mm.
- Bei einem Kreis mit Radius r = 100 km wäre der Fehler der Fläche des Quadrates ≈ -0,781 mm2
Variante 2
BearbeitenNäherungskonstruktion
Bearbeiten

Sie beruht auf der Näherung
Nach dem Ziehen des Einheitskreises ( [LE]) werden die x-Achse und die y-Achse eingetragen. Es folgen der Kreisbogen und die (nicht eingezeichnete) Mittelsenkrechte zwischen und mit Schnittpunkt . Nun wird das Lot von auf mit Fußpunkt gefällt. Das dadurch erzeugte rechtwinklige Dreieck hat wegen der Hypotenuse und des Winkels die Katheten und . Die Strecke wird in halbiert. Um den oben beschriebenen Ansatz für die Näherung zu erhalten, stellt man sich ein rechtwinkliges Dreieck mit der Hypotenuse und der kleinen Kathete vor. Mit dem Satz des Pythagoras gilt für die große Kathete
Die Länge der Kathete ist mit Zirkel und Lineal konstruierbar (siehe Animation, gleiches Konstruktions-Prinzip wie in Variante 1).
Weiter geht es mit dem Einzeichnen des rechtwinkligen Dreiecks anhand der jetzt bekannten Seiten. Hierzu wird zuerst der Punkt mithilfe einer Parallelen zur x-Achse auf die y-Achse projiziert, der Schnittpunkt ist . Der darauf folgende Kreis mit dem Radius schneidet die Parallele in und . Die Halbgerade ab durch den Kreismittelpunkt und die in errichtete Senkrechte schneiden sich in und ergeben damit das Dreieck . Der abschließende Kreis mit Radius ist der Inkreis des gesuchten Quadrates .
Fehler
BearbeitenBei einem Kreis mit Radius r = 1 [LE]:
- In GeoGebra konstruierte Seite des Quadrates [LE]
- Soll-Seite des Quadrates [LE]
- Absoluter Fehler E-12 [LE]
- Fläche des konstruierten Quadrates [FE]
- Soll-Fläche des Quadrates [FE]
- Absoluter Fehler E-12 [FE]
Verdeutlichung:
- 11 Nachkommastellen sind gleich denen von bzw. 10 Nachkommastellen sind gleich denen von .
- Bei einem Kreis mit dem Radius r = 1 Mio. km wäre der Fehler der Seite a ≈ 1,3 mm
- Bei einem Kreis mit dem Radius r = 1 km wäre der Fehler der Fläche A ≈ 5 mm2
Weblinks
Bearbeiten Quadratur des Kreises
Johann Heinrich Lambert: Beyträge zum Gebrauche der Mathematik und deren Anwendung Quadratur des Circuls, S. 157 Abgerufen am 2. Juli 2017.
Dreiteilung des Winkels
Bearbeiten- Einleitung und Erklärungen zu "Klassisches Problem", "Verallgemeinerung", "Nicht-klassische Verfahren" u. a. m. sind im Artikel Dreiteilung des Winkels enthalten.
Variante 1
BearbeitenKonstruktionsprinzip
Bearbeiten- Näherungskonstruktion
- Den gegebenen Winkel mit vier Winkelhalbierenden verkleinern und den Kreisbogen MFG zwischen Winkelhabierende w3 und w4 mit einer Näherungslösung dritteln.
Konstruktion für Winkel > 0° bis 180°
Bearbeiten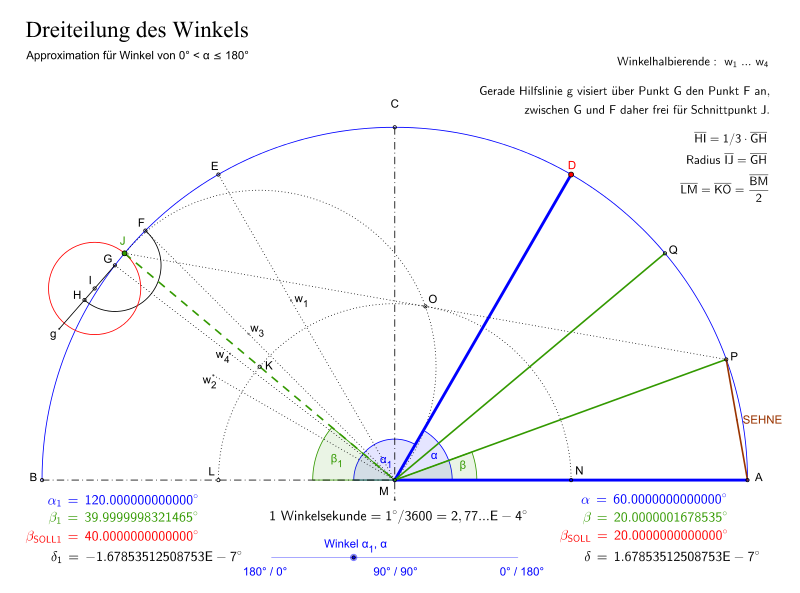
- Für Winkel < 90° ist, zur klaren Unterscheidung der Punkte die auf der geraden Hilfslinie g liegen, meist die Drittelung des Supplementwinkels vorteilhaft. Dies wird im folgenden Beispiel berücksichtigt.
- Zeichne durch den Punkt M eine Gerade.
- Zeichne um den Punkt M einen Halbkreis, es ergeben sich auf der Gerade die Schnittpunkte A und B, die Strecke MA ist der erste Winkelschenkel.
- Konstruiere eine Senkrechte zur Strecke AB ab Punkt M bis sie den Halbkreis schneidet, es ergibt sich der Schnittpunkt C.
- Konstruiere als Beispiel den Winkel = 60°, es ergibt sich der Schnittpunkt D auf dem Halbkreis MAB
- Verbinde den Punkt M mit dem Punkt D, es ergibt sich der zweite Winkelschenkel der mit der Strecke MB den Supplementwinkel = 120° einschließt.
- Konstruiere vom Winkel die Winkelhalbierende w1, es ergibt sich auf dem Halbkreis MAB der Schnittpunkt E.
- Konstruiere vom Winkel die Winkelhalbierende w2, die Länge der Strecke Mw2 etwas länger als
- Konstruiere vom Winkel die Winkelhalbierende w3, es ergibt sich auf dem Halbkreis MAB der Schnittpunkt F.
- Konstruiere vom Winkel die Winkelhalbierende w4, es ergibt sich auf dem Halbkreis MAB der Schnittpunkt G.
- Zeichne eine gerade Hilfslinie g die über den Punkt G den Punkt F anvisiert (quasi ein Lineal an die Punkte F und G angelegt), aber mit ihrer Länge, ca. Abstand |EF|, nur bis zum Punkt G verläuft und keine Verbindung der Punkte F und G herstellt. Somit ist zwischen diesen beiden Punkten der Halbkreis MAB für den späteren Schnittpunkt J frei zugänglich.
- Zeichne einen Halbkreis um den Punkt G mit dem Radius gleich dem Abstand |FG|, es ergibt sich auf der Hilfslinie g der Schnittpunkt H.
- Konstruiere auf der Hilfslinie g die Strecke HI, sie ist ein Drittel der Strecke GH.
- Zeichne einen Kreis um den Punkt I mit dem Radius gleich der Strecke GH, es ergibt sich auf dem Halbkreis MAB zwischen den Punkten F und G der Schnittpunkt J.
- Verbinde den Punkt J mit dem Punkt M, die Winkelschenkel JM und MB schließen den Winkel ein. Somit ist vorerst vom Supplementwinkel 120° ein approximiertes Drittel dargestellt. .
- Halbiere die Strecke JM, es ergibt sich darauf der Schnittpunkt K.
- Zeichne um den Punkt M einen Halbkreis der durch den Punkt K verläuft, es ergeben sich die Schnittpunkte L und N auf der Strecke AB.
- Zeichne um den Punkt K einen Halbkreis der vom Punkt M zum Punkt J verläuft, es ergibt sich der Schnittpunkt O mit dem Halbkreis MNL.
- Zeichne eine Gerade vom Punkt J durch den Punkt O bis zum Halbkreis MAB, es ergibt sich darauf der Schnittpunkt P.
- Verbinde den Punkt P mit dem Punkt M, die Winkelschenkel PM und MA schließen den Winkel ein.
- Trage die Strecke AP ab dem Punkt P einmal auf dem Halbkreis MAB ab, es ergibt sich darauf der Schnittpunkt Q. Somit ist der Winkel 60° nahezu gedrittelt.
Fehler
Bearbeiten- Der max. Winkelfehler von bzw. ist ca. 1,25E-6°, wenn der Winkel nahezu 0° bzw. nahezu 180° ist.
Beispiel um den Fehler zu verdeutlichen
Bearbeiten- Bei einem Radius r = MA = 100 km wäre der max. Fehler an der Sehne 2,2 mm
Berechnung
Bearbeiten- Im Kapitel "Neuneck", unter "Berechnung" sind zur Verifizierung des Konstruktionsprinzips alle Berechnungsschritte für die Dreiteilung des Winkels (Beispiel ) aufgezeigt. Für die Dreiteilung des oben dargestellten Supplementwinkels 120°, sind in den Formeln die entsprechenden Werte (u. a. Länge des Winkelschenkels ändert sich von 2r in r) und Bezeichnungen (Punkte, Winkel, Strecken etc.) einzusetzen.
Variante 2
BearbeitenKonstruktionsprinzip
Bearbeiten- Näherungskonstruktion
- Ein paar Konstruktionselemente stammen aus Alberts' Konstruktion.
- Mit der stark vereinfachten Konstruktion wird folgendes erreicht:
- Der größte Teil der Konstruktion liegt in der unteren Hälfte des Kreises
- Eine praktikable Dreiteilung des Winkels ab nahe bis
- Die Animation (Schrittgröße ca. 3° bis 4°) zeigt alternativ die Konstruktion für Winkel > 0° bis 90° sowie die dazu spiegelbildliche Konstruktion ab 90° bis 180°. Aus Gründen der Übersichtlichkeit sind die Punkte ohne Beschriftung.
Konstruktion für Winkel > 0° bis 180°
Bearbeiten

- Kreis mit beliebigem Durchmesser um Mittelpunkt
- Winkelschenkel und Winkelschenkel schließen den Winkel im Scheitel ein, und den Ergänzungswinkel
- Kreis um mit Radius ; die Verlängerung des Winkelschenkels schneidet Kreis in
- Durchmesser mit und Verbindung des Punktes mit
- Punkt auf Kreis so, dass
- Strecke in halbieren, die anschließende Mittelsenkrechte von schneidet in ergibt
- Parallele zu ab erreicht Kreis in
- Parallele zu ab Punkt darauf so, dass
- Linie ab durch erreicht Kreis in anschließend Linie ab bis
- Parallele zu ab erreicht Kreis in
- Strecke über hinaus verlängern, Punkt darauf so, dass
- Linie ab durch erreicht Kreis in
- Bestimme Punkt so, dass Winkel Verbindung mit ergibt den Winkel
- Mittelsenkrechte von schneidet in verbinde mit
- Bestimme Punkt so, dass Winkel
- Abschließende Verbindung mit ergibt Winkel
- Der Winkel ist nahezu gleich einem Drittel des Winkels
- Der Winkel ist nahezu gleich einem Drittel des Winkels
Fehlerbetrachtung
BearbeitenEine Fehleranalyse, ähnlich Alberts' Konstruktion, ist nicht vorhanden.
Die dargestellte Konstruktion wurde mit der Dynamische-Geometrie-Software (DGS) GeoGebra GeoGebra angefertigt; darin werden in diesem Fall die Winkelgrade meist mit signifikanten dreizehn Nachkommastellen angezeigt. Die sehr kleinen Fehler des Winkels bzw. , sprich, die Differenzwerte aus bzw. werden von GeoGebra stets mit angezeigt.
Betrachtet man die Grafik in GeoGebra, in sehr kleinen Schritten, die zu- oder abnehmenden Winkelweiten des Winkels bzw. mithilfe des Schiebereglers oder der Animation, ist vereinzelt eine max. Abweichung vom SOLL-Wert bzw. ablesbar.
Verdeutlichung des absoluten Fehlers
BearbeitenDer in GeoGebra ablesbare Differenzwert von max. entspricht einem absoluten Fehler der – nicht eingezeichneten – Sehne bzw. der sich wie folgt ergibt:
Hätten die Winkelschenkel die Länge gleich 1 Milliarde km (das Licht bräuchte für diese Strecke ≈ 56 Minuten, das ist etwas weniger als 7-mal die Entfernung Erde – Sonne), wäre der absolute Fehler der beiden – nicht eingezeichneten – Sehnen bzw. ≈ 1,7 mm.
Weblinks
BearbeitenNeuneck in diesem Buch
Supplementwinkel oder Ergänzungswinkel
Dreiteilung einer Strecke in diesem Buch
Dreiteilung des Winkels 60° in diesem Buch
Alberts' Konstruktion: Näherung für Winkelweiten größer 0° bis 90°, mit Fehleranalyse
Verdoppelung des Würfels
BearbeitenEine relativ einfache Näherungskonstruktion, aber mit einer ebenfalls außergewöhnlichen Genauigkeit ist im Folgenden beschrieben.
- Einleitung, Erklärung und Weiterführungen sind im Artikel Würfelverdoppelung enthalten.
- ist die Kantenlänge des Ausgangswürfels, die des verdoppelten Würfels
Konstruktionsbeschreibung
BearbeitenEs beginnt mit dem Einheitskreis mit Radius und dem Einzeichnen des Durchmessers . Als nächstes wird die zum Durchmesser senkrecht stehende Mittelachse eingetragen. Es folgt jeweils ein Kreisbogen mit Radius um und ; die Schnittpunkte sind und . Eine nicht eingezeichnete Mittelsenkrechte des Abstandes halbiert den Kreisbogen in . Eine Parallele zu ab ergibt die Strecke . Den Punkt bestimmt man mithilfe einer nicht eingezeichneten Mittelsenkrechten des Abstandes .
Weiter geht es mit dem Übertragen des Abstandes ab , dabei ergibt sich der Schnittpunkt . Eine Parallele zu ab ergibt die Strecke . Der Punkt wird mithilfe einer nicht eingezeichneten Mittelsenkrechten des Abstandes bestimmt. Die abschließende Verbindung des Punktes mit schneidet in und liefert somit die Strecke , deren Länge nahezu gleich dem Sollwert ist.
Fehler
BearbeitenIn GeoGebra werden max. 15 Nachkommastellen angezeigt.
Beispiel zur Verdeutlichung der Fehler
Bearbeiten- Bei einem Würfel 1 mit der Kantenlänge a1 = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 56 min.) wäre bezüglich der konstruierten Kantenlänge a2 des verdoppelten Würfels 2 kein Fehler evaluierbar.
- Somit liegt die Vemutung nahe, dass der absolute Fehler < 1 mm ist.
- Bei einem Würfel 1 mit der Kantenlänge a1 = 10 km wäre der Fehler des Volumens vom verdoppelten Würfels 2 vermutlich < 0,7 dm3 oder < 1 Liter.
Weblinks
Bearbeiten Commons: Animation, Verdoppelung des Würfels – Album mit Bildern, Videos und Audiodateien
Commons: Animation, Verdoppelung des Würfels – Album mit Bildern, Videos und Audiodateien- Quadrat
- GeoGebra
- Einheitskreis
- Mittelsenkrechte
- Messabweichung
n-Ecke mit Zahlenstrahl
BearbeitenDas Kapitel n-Ecke mit Zahlenstrahl ist noch nicht vorhanden.
Dezimalzahl als Strecke
Bearbeiten

Weitere Konstruktionen der Schulmathematik bis einschließlich 10. Jahrgangsstufe
Dezimalzahl 3,0 + 7 Nachkommastellen von Pi mit Anwendung der Strahlensätze
BearbeitenBasiskonstruktion (Schema), auch für div. ähnliche Konstruktionen anwendbar
Bearbeiten- Zeichne durch den Punkt einen Strahl . Der Strahl wird im Folgenden als Zahlenstrahl bezeichnet.
- Zeichne ab dem Punkt den Strahl , mit einem Winkel .

- Trage vier gleiche Strecken ab dem Punkt auf dem Strahl ab, es ergeben sich die Schnittpunkte , , und .
- Konstruiere den Strahl durch den Punkt parallel zum Zahlenstrahl .
- Errichte den Zahlenstrahl senkrecht auf den Strahl durch den Punkt , es ergibt sich der Schnittpunkt .
- Errichte über den Punkt den Zahlenstrahl senkrecht auf den Strahl .
- Zeichne um den Punkt einen Halbkreis, der etwas kleiner als die Strecke vom Strahl ist, und bezeichne den Schnittpunkt mit dem Strahl mit , es ergeben sich die Schnittpunkte und mit dem Zahlenstrahl .
- Trage die Strecke zweimal ab Punkt auf dem Strahl ab, es ergeben sich die Schnittpunkte und .
- Trage eine Strecke, etwas länger ein Drittel der Strecke , ab dem Punkt zehnmal auf dem Zahlenstrahl ab.
- Trage die gleiche Strecke ab dem Punkt zehnmal auf dem Zahlenstrahl ab.
- Zeichne den Diagonalstrahl durch den Punkt vom Zahlenstrahl und durch den Punkt vom Zahlenstrahl bis auf den Strahl , es ergibt sich der Scheitelpunkt .
- Zeichne den Diagonalstrahl durch den Punkt vom Zahlenstrahl und durch den Punkt vom Zahlenstrahl bis auf den Strahl , es ergibt sich der Scheitelpunkt . Somit ist das Schema konstruiert.
Konstruktion des Zählers und der Strecke
Bearbeiten- Bezeichne den Teilungspunkt vom Zahlenstrahl mit .
- Bezeichne den Teilungspunkt vom Zahlenstrahl mit .
- Projiziere den Punkt vom Zahlenstrahl mittels des Scheitelpunktes vom Strahl auf den Zahlenstrahl , es ergibt sich der Punkt . Der Wert der Zahl auf dem Zahlenstrahl ist somit nur mehr ein Zehntel des Wertes der Zahl auf dem Zahlenstrahl . Vergleiche die Strecke mit der Strecke .
- Übertrage ab dem Teilungspunkt die Strecke auf den Zahlenstrahl , es ergibt sich der Punkt .
- Projiziere den Punkt vom Zahlenstrahl mittels des Scheitelpunktes vom Strahl auf den Zahlenstrahl , es ergibt sich der Punkt .
- Übertrage ab dem Teilungspunkt die Strecke auf den Zahlenstrahl , es ergibt sich der Punkt .
- Wiederhole diesen Ablauf "Projizieren ... Übertragen" so oft, bis der Punkt auf dem Zahlenstrahl konstruiert ist.
- Konstruiere eine Parallele zum Strahl durch den Punkt bis auf den Zahlenstrahl , es entsteht der Punkt mit dem gleichen Wert wie auf dem Zahlenstrahl .
- Beachte: Bei einer Projektion des Punktes mittels des Scheitelpunktes auf den Zahlenstrahl wäre der Punkt für eine Verwendung zu nahe am Punkt .
- Projiziere den Punkt vom Zahlenstrahl mittels des Scheitelpunktes vom Strahl auf den Zahlenstrahl , es ergibt sich der Punkt .
- Übertrage ab dem Teilungspunkt die Strecke auf den Zahlenstrahl , es ergibt sich der Punkt . Somit ist der Zähler konstruiert.
- Verbinde den Punkt mit dem Punkt vom Strahl .
- Konstruiere ab dem Punkt eine Parallele zur Strecke bis auf den Strahl , es ergibt sich der Schnittpunkt .
- Übertrage ab dem Punkt die Strecke auf den Strahl , es ergibt sich der Punkt .
- Konstruiere eine Parallele zur Strecke ab dem Punkt bis auf den Zahlenstrahl , es ergibt sich der Schnittpunkt .
- Verbinde den Punkt mit dem Punkt . Die somit konstruierte Strecke hat die exakte Länge 3,1415926.
Weblinks
BearbeitenDritter Strahlensatz, Formulierung der Strahlensätze 3. Punkt
Schema für die Konstruktion von Brüchen auf Strahl
Sterne zeichnen
Bearbeiten

Stern mit 5 Zacken
BearbeitenDer fünfzackige Stern ist ein sogenanntes Sternpolygon. Das Sternpolygon lässt sich – im Gegensatz zum Stern – in einem Linienzug zeichnen.
Exakte Konstruktion
Bearbeiten- Zeichne einen Kreis um den Mittelpunkt .
- Zeichne den Durchmesser .
- Konstruiere senkrecht zu die zweite Mittelachse des Kreises, der Schnittpunkt markiert den ersten Zacken.
- Halbiere , dabei entsteht der Schnittpunkt .
- Ziehe einen Kreisbogen um mit dem Radius ab bis auf , dabei entsteht der Schnittpunkt .
- Ziehe einen Kreisbogen um mit dem Radius , die Schnittpunkte und markieren den zweiten bzw. dritten Zacken.
- Ziehe einen weiteren Kreisbogen um mit dem Radius , der Schnittpunkt markiert den vierten Zacken.
- Ziehe den letzten Kreisbogen um mit dem Radius , der Schnittpunkt markiert den fünften Zacken.
- Abschließend verbinde alle 5 Zacken mit dem jeweils übernächsten.
Einfaches Zeichnen
Bearbeiten- Zeichne einen Kreis.
- Zeichne eine Linie durch den Kreismittelpunkt.
- Einer der beiden Schnittpunkte markiert den ersten Zacken.
- Miss einen 72° Winkel am Kreismittelpunkt von der Mittellinie weg.
- Der Winkel und der Kreis markieren den zweiten Zacken.
- Nimm die Entfernung der beiden ersten Zacken als neue Einstellung für den Zirkel.
- Zeichne von den Zacken mit dem Zirkel Kreise; die Schnittpunkte zwischen den Kreisen mit dem ursprünglichem Kreis ergeben jeweils einen neuen Zacken.
- Sobald du alle 5 Zacken hast, verbinde alle Zacken mit dem jeweils übernächsten.
Stern mit 6 Zacken
BearbeitenDer sechszackige Stern – auch Davidstern genannt – ist leicht zu zeichnen.
- Zeichne einen Kreis, es ist der Umkreis des werdenden Hexagramms.
- Ziehe mit dem gleichen Radius einen Kreis mit Mittelpunkt auf dem Umkreis, er schneidet den Umkreis zweimal.
- Ziehe in gleicher Weise drei weitere Kreise mit gleichem Radius.
- Nun hast du die 6 Punkte der Zacken.
- Verbinde alle 6 Punkte jeweils mit den beiden übernächsten Punkten.
Weblinks
Bearbeiten
Dreiteilung einer Strecke
Bearbeiten

Schwerpunktmethode
Bearbeiten
- Gegeben: Eine Strecke ().
- Zeichne an ein Ende der Strecke () eine Gerade mit beliebigem Winkel ungleich Null.
- Zeichne mit dem Zirkel auf dieser Gerade in beliebigem Abstand zwei Punkte mit gleichem Abstand zum Streckenende ( und ).
- Verbinde einen der beiden Punkte mit dem anderen Ende der Strecke.
- Halbiere diese Strecke (). Man erhält Punkt .
- Verbinde diese Streckenmitte mit dem Zweiten Schnittpunkt des Kreises. Der Schnittpunkt teilt im Verhältnis 1:2.
Diese Methode ermittelt den Schwerpunkt eines Dreiecks, bei dem die gegebene Strecke eine Seitenhalbierende ist und erfordert sieben Schritte (drei davon zur Halbierung einer Stecke). Grundsätzlich sind Winkel und Radius egal, die Konstruktion wird in der Praxis bei sehr spitzem Winkel jedoch sehr ungenau.
Mit gleichseitigen Dreiecken
Bearbeiten
- Gegeben: Eine Strecke ().
- Zeichne um die beiden Enden und einen Kreis mit dem Radius . Auf diese Weise erhält man die Schnittpunkte und , welche mit und jeweils ein gleichseitiges Dreieck bilden.
- Zeichen um ebenfalls einen Kreis mit dem Radius . Man Erhält Punkt .
- Zeichne und . Der Schnittpunkt ist .
- Zeichne . Der Schnittpunkt teilt im Verhältnis 1:2.
Diese Methode baut auf der ersten auf, nutzt jedoch die Symmetrien des gleichseitigen Dreiecks und erfordert nur sechs Schritte. Wenn der Platz ausreicht, ist diese Methode besonders schnell, da der Zirkel nur einmal eingestellt werden muss.
Kreise auf Winkelhalbierenden
Bearbeiten

Kreis zwischen Winkelschenkeln und einem gegebenen Kreis
Bearbeiten
Zwei Kreise liegen auf derselben Winkelhalbierenden
Bearbeiten- Zeichne ab dem Winkelscheitel A zwei Winkelschenkel mit beliebiger Winkelweite.
- Zeichne einen Kreisbogen um A mit einem beliebigen Radius, es ergibt die Schnittpunkte B und C.
- Errichte in B eine Senkrechte zum Winkelschenkel AB.
- Errichte in C eine Senkrechte zum Winkelschenkel AC, es ergibt den Schnittpunkt M1.
- Ziehe eine Halbgerade ab A durch M1, sie ist die Winkelhalbierende ωα.
- Zeichne einen Kreisbogen um M1 mit dem Radius M1B, es ergibt den Schnittpunkt D, den ersten Berührungspunkt des gesuchten Kreises.
- Errichte in D eine Senkrechte zur Winkelhalbierenden ωα bis sie die Strecke AC in E schneidet.
- Verbinde den Punkt C mit D.
- Ziehe eine Parallele zu CD ab E bis ωα, sie liefert den Mittelpunkt M2 des gesuchten Kreises.
- Ziehe einen Kreis um M2 mit dem Radius M2D.
Somit ist der gesuchte Kreis (rot) eingearbeitet. Die Berührungspunkte sind: F und G mit den Winkelschenkeln und D mit dem benachbarten Kreis um M1.
Zwei Kreise liegen auf unterschiedlichen Winkelhalbierenden
Bearbeiten
- Zeichne ein beliebiges Dreieck ABC.
- Konstruiere die Winkelhalbierende ωα.
- Konstruiere die Winkelhalbierende ωβ.
- Bestimme beliebig den Mittelpunkt M1 des ersten Kreises auf der Winkelhalbierenden ωα.
- Konstruiere eine Senkrechte zur Strecke AB durch M1 mit Fußpunkt D.
- Zeichne den ersten Kreis um M1 durch D; es ergibt den Schnittpunkt E.
- Fälle das Lot vom Mittelpunkt M1 auf die Strecke AC mit Fußpunkt F.
- Konstruiere eine Senkrechte zur Winkelhalbierenden ωβ ab E, bis sie die Strecke AB in G schneidet.
- Ziehe einen Kreisbogen um B mit dem Radius BG, bis er die über E hinaus verlängerte Senkrechte in H schneidet.
- Hinweis: Sollte dieser Kreisbogen um B und damit der Punkt H, zu nahe an der Strecke AC liegen, verlängere die Senkrechte durch M1 über den Punkt D hinaus.
- Übertrage die Strecke DH ab G auf AB; dabei ergibt sich der Schnittpunkt I nahe am Punkt B.
- Errichte eine Senkrechte zur Strecke AB ab I bis ωβ, sie liefert den Mittelpunkt M2 des gesuchten Kreises.
- Zeichne einen Kreis um M2 durch I.
Somit ist der gesuchte zweite Kreis (rot) eingearbeitet. Die Berührungspunkte sind: I und K mit zwei Seiten des Dreiecks und J mit dem ersten Kreis um M1.
Weblinks
Bearbeiten




















































































































































































































































![{\displaystyle {\overline {AB}}\approx \;r\cdot \;0{,}684040286737349\;[LE]\;(aus\;8.2\;der\;Berechnung)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7635eb22a85e3e1fc824bcd5017496f0d05ab6d6)
![{\displaystyle Neuneckseite,\;s=r\cdot 2\cdot \sin \left({\frac {180^{\circ }}{9}}\right)\approx \;r\cdot \;0{,}684040286651337\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73103855e2e9e86f721e807224dd32c48aa0b4cd)
![{\displaystyle Fehler\;absolut,\;F_{a}={\overline {AB}}-s=r\cdot 0{,}00000000008601...\approx \;r\cdot \;8,6E-11\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2a5d78e443d9c21c9aa5ce71c49d27c6c9589b7)


![{\displaystyle s_{1}=1{,}0\;[LE]\;(aus\;9.0\;der\;Berechnung)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ead06b9a749fead8fd4cd33cee951e47c993e9ef)
![{\displaystyle r_{k}\approx 1{,}461902199897722\;[LE]\;(aus\;9.1\;der\;Berechnung)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8302498257a17ae53c4eed4fc15fcf25a4583747)
![{\displaystyle \;r\approx 1{,}461902200081543\;[LE]\;(aus\;10.1\;der\;Berechnung)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e03d59a17a2396b382128eedb4fba633edfd51da)
![{\displaystyle Fehler\;absolut,\;F_{a}=r_{k}-r=-0{,}000000000183821\ldots \approx -1{,}8E-10\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d14aca0a2c9abf265553871ab9f396de67507ad8)

![{\displaystyle {\overline {MS}}=Umkreisradius\;r=1[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/066ea9d9de86951bc8ab4804db20b03be66cfb34)


















































![{\displaystyle \mathbf {{\overline {AB}}={\frac {\overline {KR}}{2}}={\frac {sin\left({\frac {\beta }{2}}\right)\cdot 4r}{2}}=sin\left({\frac {\beta }{2}}\right)\cdot 2r\approx \;r\cdot 0{,}684040286737349} \;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64ca52d19713f2d44b6b8ec2801feb5a35071fbb)


![{\displaystyle \;s_{1}=1{,}0\;[LE]\;zum\;Beispiel}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4f9d4496b00d3d16cfbdebc4b706dfb7faf7295)


![{\displaystyle \mathbf {r_{k}={\frac {s_{1}}{2\cdot sin\left({\frac {\beta }{2}}\right)}}={\frac {1}{2\cdot sin\left({\frac {\beta }{2}}\right)}}\approx 1{,}461902199897722\;[LE]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/901efc7f664891ebe1e9a57e3b440bc7c9115e78)

![{\displaystyle s_{1}=1{,}0\;[LE]\;(aus\;9.0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb01472b6d96462879098fc69c4c7e29229ac623)


![{\displaystyle \mathbf {r={\frac {s_{1}}{2\cdot sin\left({\frac {\beta }{2}}\right)}}={\frac {1}{2\cdot sin\left({\frac {40^{\circ }}{2}}\right)}}\approx 1{,}461902200081543\;[LE]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2d146c74d4221f48a98bfce5fb5b0b2140f9ba1)
































![{\displaystyle a=0{,}563465113682859\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6df5ebf941ddd1e01a1dd207689ec5d29eaa722)
![{\displaystyle a_{SOLL}=r\cdot 2\cdot \sin \left({\frac {180^{\circ }}{11}}\right)=0{,}563465113682859...\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbbfe110b77dbfb50857a84ca80dec0ebe496994)
![{\displaystyle F_{a}=a-a_{SOLL}=0{,}0\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3e0674d11541e3d3976970cc527495746a46225)


































![{\displaystyle a=0{,}478631328575115\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6a439722bca23a54eb0c12726d71bf45eeedb4c)
![{\displaystyle a_{Soll}=r\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)=0,478631328575115534...\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471d648630fce22827887a310bc3342e61b8cf8e)
























![{\displaystyle a=0{,}445041867912629\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d2f17643600b203a59e09add9fe32a010796954)
![{\displaystyle a_{SOLL}=2\cdot \sin \left({\frac {180^{\circ }}{14}}\right)=0{,}445041867912629\ldots \;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9595b25d281da0338708457fb25e12872c0186de)

































































































![{\displaystyle 10\cdot 0{,}1{\overline {3}}=1{,}{\overline {3}}={\frac {4}{3}}\;[LE].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/669d9391b33ed16329a3d7ab397e3f19c8f306ca)




![{\displaystyle {\frac {4}{3}}\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db2cd07f7ac04ee64fbbed61b75312e45a780175)



![{\displaystyle {\overline {S_{1}M_{1}}}={\frac {1}{3}}\cdot {\overline {M_{1}L_{1}}}={\frac {1}{3}}\cdot 4={\frac {4}{3}}\;[LE].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdb6698ea1949572b7acc6ea5d42364373dc012b)


































![{\displaystyle \gamma :(0,{\tfrac {\pi }{2}}]\rightarrow \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04d8a0ec9f976fbd161120f0ec294c717a520e80)










![{\displaystyle {\overline {E_{257}E_{1}}}=a=2,44475829850863E-2\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b53ffb49e24a3c6cd4152ccb488a2091938d2ce)
![{\displaystyle a_{SOLL}=2\cdot \sin \left({\frac {180^{\circ }}{257}}\right)=2,44475829850863E-2\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a47573b3954e3dc1ad470181f078c30ed174166)
![{\displaystyle F_{a}=a-a_{SOLL}=0\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f5ab6b83a8b5c3f53c0bd5c167cb98e78fadf2a)




























![{\displaystyle a={\overline {E_{65537}E_{1}}}=9{,}58723363103780E-5\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31e5b1c3fbd3091428794d9d876957c672b16c2f)
![{\displaystyle a_{SOLL}=2\cdot \sin \left({\frac {180^{\circ }}{65537}}\right)=9{,}5872336310378200E-5\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/453d680c43dd7be36e967d25982ab3bd15d2c71d)
![{\displaystyle F_{a}=a-a_{SOLL}=-2E-19\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3354fd5327298110908fc2e5110e175556097f4b)
![{\displaystyle F_{a65537}=-F_{a}\cdot 65537=2E-19\cdot 65537=1{,}31074E-14\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb0cd39604df09e99f9d56559fc4559745cea06a)










































































































































![{\displaystyle a=1{,}772453850905516\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/510efe400f2a15cc0d516aa2b7bb3811db989201)
![{\displaystyle a_{SOLL}={\sqrt {\pi }}=1{,}772453850905516\;027\ldots \;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33639f581b3c22b73dacada0bfe7d0119f6c2b57)
![{\displaystyle A=a^{2}=3{,}141592653589793\;141\ldots \;[FE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6cae2232ab66cc43a68d16401ce1fff595c6c7f)
![{\displaystyle A_{SOLL}=\pi =3{,}141592653589793\;238\ldots \;[FE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc76e4f4559e5b6ee700cf48690cee1ff73e1a3c)
![{\displaystyle =F_{A}=a^{2}-a_{SOLL}^{2}=-9{,}67\ldots E-17\;[FE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97b21f841ae8b47a3e9441ff8f01b6d829bb0733)






















![{\displaystyle a_{2}=1{,}259921049894872\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e06a2657ad9260787b3a75da35f3bea1b0c76625)
![{\displaystyle a_{2\;SOLL}={\sqrt[{3}]{2}}=1{,}259921049894873164...\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73d15cde9fb81b8ad14681250e36b6bf546e97ea)
![{\displaystyle Fa_{2}=-1{,}16...E-15\;[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/283b8e8ddb8b1ce63b964fe4b0932ad3791bb28e)
![{\displaystyle a_{2}{^{3}}=1{,}999999999999994453...\;[VE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91158f54ce218b0bcd5ded019b873b052160e35e)
![{\displaystyle a_{2\;SOLL}{^{3}}=2{,}0\;[VE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72752c32a8596f64aec9391ebe0219a29e14e6a1)
![{\displaystyle F_{V}=a_{2}{^{3}}-a_{2\;SOLL}{^{3}}=-5{,}54...E-15\;[VE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/592243ea5eeb46432d634ac966269624216b205a)
![{\displaystyle \mathbf {\sqrt[{3}]{2}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/720f9eb7cf03b73ebc5bd89be23fb2215c1d77a2)































































































![{\displaystyle F=2\cdot \sin \left({\frac {1\cdot 10^{-13}\mathrm {^{\circ }} }{2}}\right)=0{,}000\;000\;000\;000\;001\;745\ldots =1{,}745\ldots \cdot 10^{-15}\;[\mathrm {LE} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12684260ede34dd5c2cda172dd4e5032324a8a43)


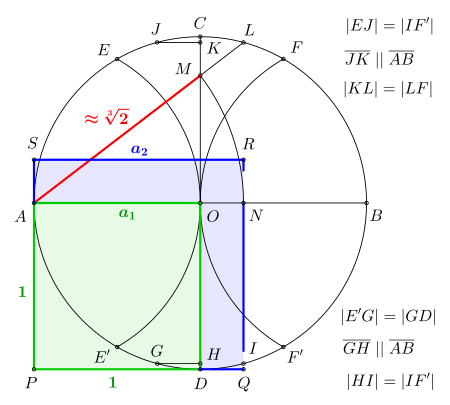









![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
![{\displaystyle {\begin{alignedat}{2}{\text{in GeoGebra konstruierte Länge der Strecke }}\qquad {\overline {AM}}&=&&1{,}259921049894873\;[\mathrm {LE} ]\\-{\text{Sollwert }}\qquad -{\sqrt[{3}]{2}}&=-&&1{,}259921049894873\dots \;[\mathrm {LE} ]\\\hline {\text{absoluter Fehler in GeoGebra nicht evaluierbar }}\qquad F&=&&0{,}000000000000000\dots \;[\mathrm {LE} ]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40521cdaf74849d920d7c9403ebbbd722919664e)









































