Verknüpfungen zwischen Mengen – Serlo „Mathe für Nicht-Freaks“

Was sind Mengenverknüpfungen? (Video vom Podcast The Wicked Mu)

Einleitendes Beispiel

Symmetrische Differenz

Stelle dir vor, du hast eine Grundmenge $M$ gegeben:

In dieser Grundmenge gibt es eine Menge $A$:

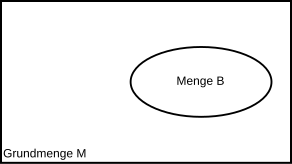
Und eine Menge $B$:

Beide Mengen haben teilweise gemeinsame Elemente, es gibt aber auch Objekte, die nur in einer der beiden Mengen enthalten sind. Insgesamt ergibt sich also folgendes Bild:

Stelle dir nun vor, wir möchten die Menge aller Objekte beschreiben, die Elemente genau einer der Mengen $A$ und $B$ sind:

Diese Menge wird symmetrische Differenz der Mengen $A$ und $B$ genannt. Man schreibt für diese symmetrische Differenz $A\,\triangle \,B$. Hier ist $\triangle$ eine Verknüpfung zwischen zwei Mengen. Der Operator $\triangle$ verknüpft nämlich zwei Mengen $A$ und $B$ zu der neuen Menge $A\,\triangle \,B$. Die neue Menge $A\,\triangle \,B$ enthält dabei alle Objekte, die Elemente genau einer der Mengen $A$ und $B$ sind. Dass $\triangle$ eine Verknüpfung ist, ist analog dazu, dass die Addition + eine Verknüpfung ist. So wie die Addition + zwei Zahlen $a$ und $b$ zu einer neuen Zahl $a+b$ verknüpft, genauso verknüpft auch die symmetrische Differenz $\triangle$ zwei Mengen $A$ und $B$ zu einer neuen Menge $A\,\triangle \,B$. Beispiel:

Genauso wie die Addition aus den beiden Zahlen $4$ und $7$ die Summe $4+7=11$ macht, verknüpft die symmetrische Differenz $\triangle$ die beiden Mengen $\{1,4\}$ und $\{4,7\}$ zur neuen Menge $\{1,4\}\,\triangle \,\{4,7\}=\{1,7\}$.

Komplement

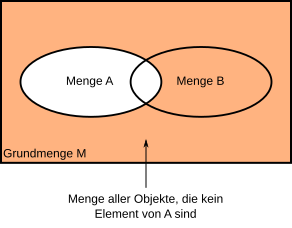
Schauen wir uns noch ein weiteres Beispiel an: Stelle dir vor, wir wollen alle Objekte der Grundmenge beschreiben, die nicht in $A$ enthalten sind:

Diese Menge aller Objekte der Grundmenge, die nicht in $A$ enthalten sind, wird Komplement von $A$ genannt. Für diese Menge schreibt man $A^{\rm {C}}$. Während im obigen Beispiel $\triangle$ der Operator war, ist hier $\cdot ^{\rm {C}}$ der Operator. Im Unterschied zu $\triangle$ wirkt $\cdot ^{\rm {C}}$ auf nur einer Menge. Während nämlich $\triangle$ zwei Mengen $A$ und $B$ zu einer neuen Menge $A\,\triangle \,B$ verknüpft, nimmt $\cdot ^{\rm {C}}$ nur eine Menge $A$ und macht daraus die neue Menge $A^{C}$.

Überblick zu allen Mengenverknüpfungen

So wie die symmetrische Differenz und das Komplement gibt es mehrere auf Mengen definierten Verknüpfungen. In der nachfolgenden Übersicht geben wir zunächst eine Übersicht über die wichtigsten Mengenverknüpfungen. In den nächsten Kapiteln werden wir diese dann einzeln vorstellen.

Name der Verknüpfung	Schreibweise	Aussprache	Mengendiagramm	Definition	Erklärung
Durchschnitt	$A\cap B$	„$A$ geschnitten $B$“		$A\cap B:=\{x\,|\,x\in A\land x\in B\}$	Die Menge aller Objekte, die sowohl in der Menge $A$ als auch in der Menge $B$ enthalten sind
Vereinigung	$A\cup B$	„$A$ vereinigt $B$“		$A\cup B:=\{x\,|\,x\in A\lor x\in B\}$	Die Menge aller Objekte, die in der Menge $A$ oder in der Menge $B$ enthalten sind (hier ist „oder“ als „und/oder“, also als einschließendes Oder, zu lesen)
Differenz	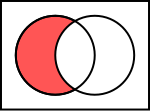$A\setminus B$	„$A$ ohne $B$“		$A\setminus B:=\{x\,|\,x\in A\land x\notin B\}$	Die Menge aller Objekte, die in der Menge $A$ enthalten sind und keine Elemente der Menge $B$ sind
Symmetrische Differenz	$A\,\triangle \,B$	„symmetrische Differenz von $A$ und $B$“		$A\,\triangle \,B:=\{x\,|\,x\in A\,{\dot {\lor }}\,x\in B\}$	Die Menge aller Objekte, die in genau einer der Mengen $A$ und $B$ enthalten sind, also entweder in A oder in B, aber nicht in beiden
Komplement	$A^{\rm {C}}$	„Komplement von $A$“		$A^{\rm {C}}:=\{x\,|\,x\notin A\}$	Die Menge aller Objekte (der Grundmenge), die keine Elemente von $A$ sind