Sinus und Kosinus – Serlo „Mathe für Nicht-Freaks“

In diesem Kapitel behandeln wir die beiden trigonometrischen Funktionen Sinus und Kosinus. Sie bilden die wichtigsten trigonometrischen Funktionen und werden unter anderem in der Geometrie für Dreiecksberechnungen sowie der Trigonometrie benötigt. Wellen wie elektromagnetische Wellen sowie harmonische Schwingungen lassen sich über Sinus- beziehungsweise Kosinusfunktionen beschreiben, sodass diese in der Physik allgegenwärtig sind.

Definition über Einheitskreis

Es gibt mehrere Möglichkeiten, den Sinus und den Kosinus zu definieren. Aus der Schule wird dir möglicherweise schon die Definition vom Sinus und Kosinus am Einheitskreis bekannt sein. Dabei wird ein Punkt $P(x,y)$ betrachtet, der sich auf einem Kreis um den Ursprung mit Radius $r=1$ befindet. Die $x$-Achse schließt mit der Strecke vom Nullpunkt zu $P(x,y)$ den Winkel $\theta$ ein:

Der Punkt P auf dem Einheitskreis mit den Koordinaten (x,y)

Der Winkel $\theta$ legt eindeutig fest, wo sich der Punkt $P(x,y)$ befindet. Damit kann die $x$-Koordinate und die $y$-Koordinate jeweils durch eine von $\theta$ abhängige Funktion beschrieben werden. Diese Funktionen $x(\theta )$ und $y(\theta )$ nennen wir die Sinusfunktion $\sin(\theta )$ beziehungsweise Cosinusfunktion $\cos(\theta )$:

Die Sinus und Kosinusfunktion am Einheitskreis

Im Folgenden nehmen wir $x$ als Winkel und schreiben $\sin(x)$ anstelle von $\sin(\theta )$ beziehungsweise $\cos(x)$ anstatt $\cos(\theta )$. Damit ergibt sich folgende Definition:

Definition (Definition Sinus und Kosinus am Einheitskreis)

Sei $P$ der Punkt auf dem Einheitskreis, dessen Ortsvektor mit der horizontalen Koordinatenachse den Winkel $x$ einschließt. Die Koordinaten von $P$ werden dann $(\cos(x),\sin(x))$ genannt. Dabei nennt man $\cos(x)$ den Kosinus von $x$ und $\sin(x)$ den Sinus von $x$.

Graph der Sinus und Kosinusfunktion

Die folgende Animation zeigt, wie die Graphen der Sinus- beziehungsweise Kosinusfunktion schrittweise konstruiert werden:

Animation zur Definition des Sinus und des Kosinus am Einheitskreis

Damit ergibt sich folgender Graph für die Sinusfunktion:

Graph der Sinusfunktion

Für die Kosinusfunktion erhalten wir:

Graph der Kosinusfunktion

Definition über Exponentialfunktion

Darstellung über komplexe Exponentialfunktion

Die Sinus- und Kosinusfunktion kann auch als Summe von gewissen komplexen Exponentialfunktionen definiert werden. Mit dieser Darstellung können besonders elegant Eigenschaften vom Sinus und Kosinus nachgewiesen werden.

Definition (Sinus und Kosinus über komplexe Exponentialfunktion)

Wir definieren die Funktionen $\sin$ (Sinus) und $\cos$ (Kosinus) durch

${\begin{aligned}&\sin :\mathbb {R} \to \mathbb {R} :x\mapsto {\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)\\[0.3em]&\cos :\mathbb {R} \to \mathbb {R} :x\mapsto {\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)\end{aligned}}$

Diese Funktionen sind wohldefiniert: Für jede reelle Zahl $x$ ist die komplexe Zahl $\mathrm {e} ^{-\mathrm {i} x}$ die komplex Konjugierte von $\mathrm {e} ^{\mathrm {i} x}$. Damit ist $\mathrm {e} ^{ix}+\mathrm {e} ^{-ix}$ eine reelle Zahl und es gilt $\cos(x)={\tfrac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)\in \mathbb {R}$. Auf analoge Art kann man zeigen, dass $\sin(x)={\tfrac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)\in \mathbb {R}$ ist.

Herleitung der Exponentialdefinition

Man kann zeigen, dass $e^{\mathrm {i} \theta }$ der Punkt auf dem Einheitskreis ist, dessen Ortsvektor mit der $x$-Achse den Winkel $\theta$ einschließt:

e^(iθ) im Einheitskreis

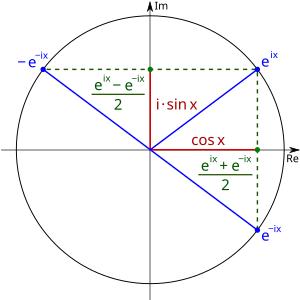
Der Realteil der komplexen Zahl $e^{\mathrm {i} \theta }$ ist damit $\cos(\theta )$, und der Imaginärteil ist $\sin(\theta )$. Es gilt also $e^{\mathrm {i} \theta }=\cos(\theta )+\sin(\theta )\mathrm {i}$. Bei $e^{-\mathrm {i} \theta }$ betrachten wir den Winkel $-\theta$. Der Punkt $e^{-\mathrm {i} \theta }$ liegt gespiegelt an der reellen Achse auf der anderen Seite:

e^(-iθ) im Einheitskreis

Damit ist der Realteil von $e^{-\mathrm {i} \theta }$ derselbe wie bei $e^{\mathrm {i} \theta }$, also $\cos(\theta )$. Jedoch ist der Imaginärteil gegenüber $e^{\mathrm {i} \theta }$ um die Zahl $-1$ multipliziert und damit gleich $-\sin(\theta )$. Wir erhalten $e^{-\mathrm {i} \theta }=\cos(\theta )-\sin(\theta )\mathrm {i}$. Also haben wir:

${\begin{aligned}e^{\mathrm {i} \theta }&=\cos(\theta )+\sin(\theta )\mathrm {i} \\[0.3em]e^{-\mathrm {i} \theta }&=\cos(\theta )-\sin(\theta )\mathrm {i} \end{aligned}}$

Durch Addition beider Gleichungen erhalten wir:

$e^{\mathrm {i} \theta }+e^{-\mathrm {i} \theta }=2\cos(\theta )\implies \cos(\theta )={\frac {1}{2}}\left(e^{\mathrm {i} \theta }+e^{-\mathrm {i} \theta }\right)$

Und durch Subtraktion der beiden Gleichungen ergibt sich:

$e^{\mathrm {i} \theta }-e^{-\mathrm {i} \theta }=2\sin(\theta )\mathrm {i} \implies \sin(\theta )={\frac {1}{2\mathrm {i} }}\left(e^{\mathrm {i} \theta }-e^{-\mathrm {i} \theta }\right)$

Damit haben wir die beiden Definitionen $\sin(x)={\tfrac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)$ und $\cos(x)={\tfrac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)$ hergeleitet. Diese Herleitung ist noch einmal in folgender Grafik illustriert:

Herleitung der komplexen Exponentialdarstellung des Sinus und Kosinus

Reihendarstellung vom Sinus und Kosinus

Definition als Reihe

Diese Animation illustriert die Definition der Sinusfunktion durch eine Reihe. Je höher die Zahl $N$ ist, desto mehr Summanden werden in der Reihendefinition verwendet. So ist bei $N=2$ neben der Sinusfunktion zusätzlich das kubische Polynom $\sum _{k=0}^{2-1}{\tfrac {(-1)^{k}}{(2k+1)!}}x^{2k+1}=x-{\tfrac {x^{3}}{6}}$ eingezeichnet.

In der Vorlesung wird oft eine andere Definition bevorzugt, nämlich die sogenannte Reihendarstellung, bei der der Sinus und Kosinus über eine Reihe definiert wird. Die Reihendarstellung ist zwar weniger anschaulich als die Definition über dem Einheitskreis, mit ihr können aber einige Eigenschaften des Sinus und Kosinus leichter bewiesen werden. Außerdem kann mit ihr der Sinus und Kosinus auf komplexe Zahlen erweitert werden.

Definition (Sinus und Kosinus)

Wir definieren die Funktionen $\sin$ (Sinus) und $\cos$ (Kosinus) durch

${\begin{aligned}&\sin :\mathbb {R} \to \mathbb {R} ,x\mapsto \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}\\[0.3em]&\cos :\mathbb {R} \to \mathbb {R} ,x\mapsto \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}\end{aligned}}$

Wohldefiniertheit der Reihendarstellung

Wir müssen nachweisen, dass unsere Reihendarstellung der Sinus- und Kosinusfunktion wohldefiniert ist. Sprich: Wir müssen zeigen, dass für alle $x\in \mathbb {R}$ die Reihen $\sum _{k=0}^{\infty }{\tfrac {(-1)^{k}}{(2k+1)!}}x^{2k+1}$ beziehungsweise $\sum _{k=0}^{\infty }{\tfrac {(-1)^{k}}{(2k)!}}x^{2k}$ gegen eine reelle Zahl konvergieren.

Satz

Für alle reelle Zahlen $x$ konvergieren die Reihen $\sum _{k=0}^{\infty }{\tfrac {(-1)^{k}}{(2k+1)!}}x^{2k+1}$ und $\sum _{k=0}^{\infty }{\tfrac {(-1)^{k}}{(2k)!}}x^{2k}$.

Beweis

Wir beweisen den Satz für die Reihe $\sum _{k=0}^{\infty }{\tfrac {(-1)^{k}}{(2k+1)!}}x^{2k+1}$ der Sinusfunktion. Der Beweis für die Reihe der Kosinusfunktion kann analog geführt werden. Für $x=0$ finden wir zunächst:

${\begin{aligned}&\sum _{k=0}^{\infty }{{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ x=0\right.}\\[0.3em]=\ &\sum _{k=0}^{\infty }{{\frac {(-1)^{k}}{(2k+1)!}}0^{2k+1}}\\[0.3em]=\ &\sum _{k=0}^{\infty }{0}=0\end{aligned}}$

Für $x=0$ konvergiert die Reihe demnach. Für $x\neq 0$ wenden wir das Quotientenkriterium an. Sei hierzu $a_{k}:={\tfrac {(-1)^{k}}{(2k+1)!}}x^{2k+1}$ für alle $k\in \mathbb {N} _{0}$, so dass wir $\sum _{k=0}^{\infty }{{\tfrac {(-1)^{k}}{(2k+1)!}}x^{2k+1}}=\sum _{k=0}^{\infty }{a_{k}}$ haben. Es gilt:

${\begin{aligned}&\lim _{k\to \infty }{\left|{\frac {a_{k+1}}{a_{k}}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|-{\frac {x^{2(k+1)+1}\cdot (2k+1)!}{x^{2k+1}\cdot (2(k+1)+1)!}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|-{\frac {x^{2k+3}\cdot (2k+1)!}{x^{2k+1}\cdot (2k+3)!}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|{\frac {x^{2}}{(2k+2)(2k+3)}}\right|}=0\end{aligned}}$

Wegen $\lim _{k\to \infty }{\left|{\tfrac {a_{k+1}}{a_{k}}}\right|}=0$ konvergiert die Reihe nach dem Quotientenkriterium.

Äquivalenz der Exponential- und Reihendarstellung

Wir haben mehrere Definitionen der Sinus- und Kosinusfunktion kennen gelernt. Einen Zusammenhang zwischen der Exponentialdarstellung und der Definition am Einheitskreis haben wir bereits hergestellt. Nun müssen wir noch zeigen, dass die Exponential- und die Reihendarstellung äquivalent zueinander sind.

Satz

Es gilt für alle $x\in \mathbb {R}$:

${\begin{aligned}\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}&={\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)\\[0.5em]\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}&={\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)\end{aligned}}$

Damit ist es egal, ob die Sinus- bzw. Kosinusfunktion über ihre Reihendarstellung oder über ihre Exponentialdarstellung definiert wird.

Beweis

Wir wissen bereits vom Kapitel über die Exponentialfunktion, dass die Exponentialfunktion die Reihendarstellung $\exp(x)=\sum _{k=0}^{\infty }{\tfrac {x^{k}}{k!}}$ hat. Wenn wir nun $\mathrm {i} {\tilde {x}}$ für $x$ in die Reihendarstellung einsetzen, erhalten wir:

${\begin{aligned}\mathrm {e} ^{\mathrm {i} {\tilde {x}}}&=\sum _{k=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{k}}{k!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ {\text{absolute Konvergenz}}\implies {\text{Reihe aufspalten}}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{2l}}{(2l)!}}+\sum _{l=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{2l+1}}{(2l+1)!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ \mathrm {i} ^{2l}=(-1)^{l}{\text{und }}\mathrm {i} ^{2l+1}=\mathrm {i} \cdot (-1)^{l}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l)!}}{\tilde {x}}^{2l}+\mathrm {i} \sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l+1)!}}{\tilde {x}}^{2l+1}\end{aligned}}$

Nun setzen wir $-\mathrm {i} {\tilde {x}}$ in die Reihendarstellung der Exponentialfunktion ein:

${\begin{aligned}\mathrm {e} ^{-\mathrm {i} {\tilde {x}}}&=\sum _{k=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{k}}{k!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ {\text{absolute Konvergenz}}\implies {\text{Reihe aufspalten}}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{2l}}{(2l)!}}+\sum _{l=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{2l+1}}{(2l+1)!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ (-\mathrm {i} )^{2l}=(-1)^{l}{\text{und }}(-\mathrm {i} )^{2l+1}=-\mathrm {i} \cdot (-1)^{l}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l)!}}{\tilde {x}}^{2l}-\mathrm {i} \sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l+1)!}}{\tilde {x}}^{2l+1}\end{aligned}}$

Schreiben wir $\alpha (x)=\sum _{k=0}^{\infty }{\tfrac {(-1)^{k}}{(2k)!}}x^{2k}$ und $\beta (x)=\sum _{k=0}^{\infty }{\tfrac {(-1)^{k}}{(2k+1)!}}x^{2k+1}$. So haben wir gezeigt, dass

${\begin{aligned}\mathrm {e} ^{\mathrm {i} {\tilde {x}}}&=\alpha (x)+\mathrm {i} \beta (x)\\\mathrm {e} ^{-\mathrm {i} {\tilde {x}}}&=\alpha (x)-\mathrm {i} \beta (x)\\\end{aligned}}$

Es folgt für die Differenz

$\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{\mathrm {-i} x}=\alpha (x)+\mathrm {i} \beta (x)-(\alpha (x)-\mathrm {i} \beta (x))=\mathrm {2i} \cdot \beta (x)$

Damit ist:

$\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}=\beta (x)={\tfrac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)$

Analog ist:

$\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{\mathrm {-i} x}=\alpha (x)+\mathrm {i} \beta (x)+(\alpha (x)-\mathrm {i} \beta (x))=\mathrm {2} \cdot \alpha (x)$

Es folgt:

$\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}=\alpha (x)={\tfrac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)$