Inhalte auf Ringen – Serlo „Mathe für Nicht-Freaks“
In diesem Artikel lernen wir die Grundbegriffe der Maßtheorie kennen. Wir überlegen uns zuerst, was "Messen" von Größen eigentlich ist und welche Eigenschaften eine Messfunktion haben sollte. Als sinnvollen Definitionsbereich für solche Messfunktionen führen wir Mengenringe ein. Damit können wir definieren, was ein Inhalt auf einem Ring ist.
Extensive Größen
Bearbeiten"Messen" im Sinne der Maßtheorie meint quantifizieren: Gefragt ist nicht "welchen Wert hat ...?", "wie schnell/heiß/hell ist ...?", sondern "wie viel von ...?", "wie groß/schwer/zahlreich ist ..?". Uns interessieren also Größen, die sich mit der Größe des zugrundeliegenden Systems ändern. In der Physik werden Größen mit dieser Eigenschaft extensive Größen genannt. Ein Beispiel dafür ist die Masse: Fügen wir zwei Körper und mit Masse und zusammen, so hat der entstehende Körper die größere Masse . Größen, die sich nicht mit der Größe des zugrundeliegenden Systems ändern, heißen auch intensiv. Zum Beispiel ist die Temperatur eine intensive Größe: das Zusammengießen zweier Flüssigkeiten einer Temperatur führt nicht zur Summe der Temperaturen.
Wann immer wir also in der Maßtheorie etwas "quantifizieren", dann messen wir eine extensive Größe. Weitere Beispiele für solche Größen sind:
Beispiel (Extensive Größen)
- geometrische Volumina: die Länge einer Strecke, der Flächeninhalt einer Ebene oder Oberfläche, das Volumen eines Körpers, ... es sind sogar Volumina von Objekten nichtganzzahliger Dimension denkbar (Fraktale)
- die einem physikalischen System enthaltene Energie
- die Stoffmenge (wie viele Atome?)
- die elektrische Ladung auf einem Körper
- aber auch: die Wahrscheinlichkeit von Ereignissen. Wenn mehr mögliche Ergebnisse eines Zufallsexperiments zu einem Ereignis gehören, dann steigt auch die Wahrscheinlichkeit, dass das Ereignis eintritt.
Wir können die Maßtheorie also als mathematische Theorie des Messens extensiver Größen auffassen.
Messfunktionen
BearbeitenWie können wir das Messen solcher Größen mathematisch fassen? Offenbar wird durch das Messen einer Größe eine Zuordnung beschrieben: Gewissen Objekten (Körpern, Ereignissen, Ansammlungen) wird jeweils genau ein (verallgemeinertes) Volumen zugeordnet. Das Messen einer Größe kann also durch eine Funktion beschrieben werden. Der Definitionsbereich dieser Funktion beinhaltet die zu messenden Objekte. Diese können als Teilmengen einer Grundgesamtheit aufgefasst werden. Beispielsweise kann man (physikalische) Körper als Teilmengen des sehen:
Beispiel (Körper als Teilmengen des )
Quader lassen sich z.B. durch Mengen der Form beschreiben, wobei die sind. Oft ist es geschickter, statt abgeschlossener Intervalle halboffene der Form zu benutzen: Die daraus gebildeten "halboffenen Quader" lassen sich disjunkt und lückenlos aneinanderfügen.
Eine Kugel mit Mittelpunkt im Ursprung und Radius wird durch die Menge beschrieben.
Genauso kann man zum Beispiel Teilmengen von betrachten, wenn es beim Messen einer extensiven Größe um das Zählen von Objekten geht. Der Definitionsbereich wird also ein Mengensystem von Teilmengen einer (jeweils genauer zu bestimmenden) Grundmenge sein und die Funktion eine Mengenfunktion. Die Funktionswerte der Funktion entsprechen den diesen Mengen zugeordneten Volumina und sind Skalare aus . Wir wollen eine solche Funktion vorerst "Messfunktion" nennen.
Definition (Messfunktion)
Das Messen einer extensiven Größe formalisieren wir über eine Mengenfunktion auf einem System von Teilmengen einer Grundmenge mit Werten in . Eine solche Mengenfunktion
die das Messen einer extensiven Größe beschreibt, nennen wir eine Messfunktion (auf ).
Mathematisch gesehen ist für uns eine Messfunktion zunächst nichts weiter als eine Mengenfunktion mit Werten in . Wir untersuchen, welche weiteren Eigenschaften eine Messfunktion haben sollte, um sinnvoll das Messen einer extensiven Größe beschreiben zu können.
Welche Eigenschaften sollte eine Messfunktion haben?
BearbeitenNichtnegativität
BearbeitenEs ist intuitiv sinnvoll, Nichtnegativität von Messfunktionen zu verlangen. Denn wie soll ein negatives Volumen zu interpretieren sein? Zwar gibt es Situationen, in denen man auch negative Zahlen als Werte einer Messfunktion zulässt (signierte Maße). Anschaulich entspricht das dem Messen einer Gesamtladung, die sich aus positiven und negativen Anteilen zusammensetzt. Manchmal wird der Wertebereich sogar noch weiter verallgemeinert, sodass auch komplexe Zahlen als Funktionswerte auftreten können (komplexe Maße) oder gewisse lineare Abbildungen (Spektralmaße). Alle diese Fälle ergeben sich aber als Verallgemeinerungen aus der nichtnegativen reellen Situation, sodass wir uns vorerst darauf beschränken wollen. Außerdem sollte auch Unendlich als Funktionswert zugelassen sein: Beispielsweise sollte das geometrische Volumen von unendlich sein. Wir fordern also: Eine Messfunktion bildet nach ab.
Monotonie
BearbeitenMessfunktionen sollen das Messen extensiver Größen formalisieren. Extensive Größen sind dadurch charakterisiert, dass sie sich mit der Größe des zugrundeliegenden Systems ändern. Insbesondere sollte ein Vergrößern des Systems nicht zu einer Verkleinerung der gemessenen Größe führen. Beispielsweise sollte man beim Bestimmen der Anzahl der Atome in einer Stoffprobe nach dem Hinzufügen einer gewissen Menge des Stoffs nicht weniger Atome zählen. Diese Eigenschaft sollte sich auch bei der Messfunktion finden. Mathematisch lässt sich das mit dem Begriff der Monotonie einer Mengenfunktion beschreiben:
Definition (Monotone Mengenfunktion)
Eine Mengenfunktion heißt monoton, falls für alle Mengen mit gilt, dass ist.
Wir fordern also: Eine Messfunktion ist monoton.
Subadditivität
Bearbeiten

Die Monotonie der Messfunktion garantiert, dass der Wert für eine gegebene Menge stets kleiner oder gleich dem Wert für eine beliebige Obermenge ist. Aber gilt das auch, wenn die Obermenge eine Vereinigung von mehreren Mengen ist? Intuitiv sollte das der Fall sein: Wird eine Menge mit Mengen überdeckt, dann sollte die Messfunktion für auf keinen Fall einen größeren Wert liefern als für die Summe der Inhalte der überdeckenden Mengen.
Mathematisch ausgedrückt: Für eine Messfunktion und Mengen sollte gelten:
Insbesondere sollte diese Eigenschaft erfüllt sein, wenn die Vereinigung der überdeckenden Mengen selbst nicht mehr im Defintionsbereich liegt. Doch diese Eigenschaft wird noch nicht durch die Monotonie ausgedrückt!
Beispiel
Betrachte die Grundmenge und das Mengensystem . Die Mengenfunktion sei definiert durch und . Offenbar ist monoton. Jedoch gilt die Monotonie nicht mehr für endliche Überdeckungen! Es ist , aber
Die Eigenschaft von Mengenfunktionen, dass die Monotonie auch bei endlichen Überdeckungen erhalten bleibt, muss also extra gefordert werden. Man nennt das (endliche) Subadditivität.
Definition ((Endlich) subadditive Mengenfunktion)
Eine Mengenfunktion heißt (endlich) subadditiv, falls für alle und beliebige Mengen gilt:
Falls die Überdeckung der Menge nur aus einer einzigen Menge besteht, entspricht diese Eigenschaft genau der Monotonie. Wir können also die Subadditivität als Verallgemeinerung der Monotonie auffassen und die Forderung der Monotonie von Messfunktionen ersetzen durch diese verallgemeinerte Version: Messfunktionen sollen subadditiv sein.
Additivität
BearbeitenDie bisher geforderten Eigenschaften der Monotonie bzw. allgemeiner der Subadditivität machen nur eine "approximative" Aussage: Die Funktionswerte einer subadditiven Mengenfunktion können vom "echten" Wert nach oben abweichen. Um das zu verdeutlichen ein
Beispiel (Subadditivität als äußere Approximation)
Seien und . Die Mengenfunktion mit und ist subadditiv, denn es gilt . Intuitiv würden wir von einer Messfunktion aber erwarten.

Offenbar muss also für eine Messfunktion, die "exakt" sein soll, diese Eigenschaft zusätzlich gefordert werden: Wird eine Menge von endlich vielen, paarweise disjunkten Mengen genau überdeckt, dann soll der Funktionswert der Messfunktion für gleich der Summe der Funktionswerte für die einzelnen sein.
Um hervorzuheben, dass eine Vereinigung eine Vereinigung paarweise disjunkter Mengen ist, führen wir eine neue Schreibweise ein:
Definition (Disjunkte Vereinigung)
Eine Vereinigung von Mengen heißt disjunkt, wenn die paarweise disjunkt sind, und wir schreiben
Die oben formulierte Bedingung der "Exaktheit" einer Mengenfunktion, dass passgenaues Überdecken bzw. Zerlegen und Wieder-Zusammensetzen einer Menge ihr Volumen nicht ändert, heißt (endliche) Additivität:
Definition ((Endlich) additive Mengenfunktion)
Eine Mengenfunktion heißt (endlich) additiv, falls für alle und alle paarweise disjunkten Mengen mit gilt:
Diese wünschenswerte Eigenschaft einer Messfunktion, exakt zu sein, halten wir fest und fordern also: Messfunktionen sind additiv.
Warnung
Beachte: In der Definition der Additivität stellen wir die einschränkende Bedingung, dass die Vereinigung der ebenfalls im Mengensystem liegt, damit die linke Seite der Gleichung sinnvoll ist. Das war bei der Subadditivität nicht nötig, weil es nur um die Überdeckung (und nicht Zerlegung) einer Menge ging.
Es ist wichtig zu bemerken, dass aufgrund dieser einschränkenden Bedingung die Additivität einer Mengenfunktion mehr noch als die Subadditivität vom Definitionsbereich abhängt. Insbesondere folgt aus der Additivität einer Mengenfunktion im Allgemeinen nicht ihre Subadditivität oder Monotonie. Das liegt daran, dass eine Mengenfunktion trivialerweise additiv sein kann, einfach weil ihr Definitionsbereich keine disjunkten Mengen enthält:
Beispiel (Eine additive, aber nicht monotone Mengenfunktion)
Sei ein Mengensystem und eine Mengenfunktion darauf mit und . Dann ist natürlich additiv, aber nicht subadditiv, nicht einmal monoton.
Jedoch werden wir später sehen, dass Additivität die Subadditivität impliziert, wenn der Definitionsbereich genügend "Struktur" aufweist.
Zuletzt macht es die Additivität von Messfunktionen wünschenswert, dass gilt: Wegen der Additivität muss gelten, und diese Bedingung ist nur für oder erfüllbar. Wäre nun , so müsste aufgrund der Monotonie für alle Mengen gelten. Um diesen pathologischen Fall auszuschließen, fordert man zusätzlich: Für Messfunktionen gilt .
Zusammenfassung
BearbeitenWir halten die Eigenschaften fest, die eine Messfunktion haben sollte, um sinnvoll das Messen einer extensiven Größe zu beschreiben:
- Eine solche Funktion sollte nach abbilden. Intuitiv ist das sinnvoll, außerdem lassen sich alle weiteren Fälle von dieser Situation aus verallgemeinern.
- Sie sollte subadditiv sein. Die Subadditivität haben wir als eine verbesserte Form der Monotonie hergeleitet, die auch bei endlichen Überdeckungen erhalten bleibt. Insbesondere ist jede subadditive Mengenfunktion auch monoton. Die Monotonie selbst spiegelt die charakteristische Eigenschaft extensiver Größen wieder, sich mit der Größe des betrachteten Systems zu ändern.
- Sie sollte additiv sein. Die Additivität entspricht der Eigenschaft einer Messfunktion, "exakt" zu sein und sich mit dem Zerlegen gemessener Objekte in endlich viele Teile und dem Wieder-Zusammensetzen zu vertragen.
- Sie sollte der leeren Menge den Wert Null zuordnen. Das ist intuitiv sinnvoll und dient außerdem dazu, den Fall auszuschließen, dass die Messfunktion konstant unendlich ist.
Die Frage nach dem Definitionsbereich
BearbeitenIn den Überlegungen zur Additivität hat sich schon eine Schwierigkeit abgezeichnet: Ob eine Mengenfunktion additiv ist, hängt auch von ihrem Definitionsbereich ab. Es ist klar: Je mehr Mengen im Definitionsbereich enthalten sind, umso schwieriger ist es, die Additivität für alle diese Mengen sicherzustellen. Deshalb stellt sich die Frage, welches (möglichst umfassende) Mengensystem über einer Grundmenge man überhaupt als Definitionsbereich einer bestimmten Messfunktion wählen kann, ohne ihre Additivität zu gefährden. In der Tat ist die Antwort auf diese Frage im Allgemeinen nicht einfach die Potenzmenge . Überraschenderweise ist es nicht möglich, jede additive und subadditive Messfunktion auf der gesamten Potenzmenge der Grundmenge zu definieren. Ein Beispiel ist das elementargeometrische Volumen auf dem :
Exkurs: Das Inhaltsproblem
BearbeitenDas Ziel ist, eine additive Mengenfunktion zu definieren, die das elementargeometrische Volumen im beschreibt. Das Problem, eine solche Funktion auf ganz zu definieren, kann man dadurch angehen, indem man sich anschaut, welche formalen Eigenschaften sie erfüllen sollte. Drei Eigenschaften, die auf jeden Fall gelten sollten, werden im sogenannten Inhaltsproblem gefordert:
Definition (Das Inhaltsproblem)
Gesucht ist eine auf der Potenzmenge des erklärte "Inhaltsfunktion" mit folgenden Eigenschaften:
- endliche Additivität
- Bewegungsinvarianz: Für jede Bewegung und für alle gilt . (Eine Bewegung ist eine affin-lineare Transformation von der Form mit und orthogonalem linearem Anteil , also eine Drehung, Spiegelung oder Verschiebung im Raum)
- Normiertheit:
Hausdorff, Banach und Tarski haben aber zeigen können:
- Das Inhaltsproblem ist unlösbar für den , falls . (Hausdorff, 1914)
- Das Inhaltsproblem ist lösbar für den und den , aber es ist nicht eindeutig lösbar. (Banach, 1923)
Aufbauend auf dem Resultat von Hausdorff haben Banach und Tarski den folgenden Satz gezeigt, welcher auch als "Banach-Tarski-Paradoxon" bekannt ist:
Satz (Satz von Banach und Tarski (1924))
Sei und seien beschränkte Mengen mit nicht-leerem Inneren. Dann gibt es Mengen und Bewegungen , so dass die disjunkte Vereinigung der Mengen ist und die disjunkte Vereinigung der Mengen .
Dieser Satz macht anschaulich klar, dass das Inhaltsproblem auf dem für nicht lösbar sein kann. Die Implikationen wären absurd: Aus dem Satz folgt, dass sich eine Erbse geeignet in endlich viele Teile zerlegen und zu einer Kugel von der Größe der Sonne zusammensetzen lässt. (Natürlich funktioniert das nicht im echten Leben, allein deshalb, weil physikalische Körper keine kontinuierlichen Punktmengen, sondern aus Atomen zusammengesetzt sind. Die Mengen einer solchen Zerlegung sind äußerst komplex und lassen sich am ehesten als "Punktwolken" veranschaulichen, die sich im Allgemeinen nicht explizit angeben lassen.)
Warnung
Obwohl das Inhaltsproblem für unlösbar ist, gibt es nicht bei jeder Messfunktion Schwierigkeiten, wenn man sie auf der ganzen Potenzmenge definieren möchte. Es hängt von den gewünschten Eigenschaften der Messfunktion und von der betrachteten Grundmenge ab, ob das möglich ist: Beim Inhaltsproblem sind es vor allem die Bewegungsinvarianz und die Grundmenge für , die Schwierigkeiten machen. Es kann aber bei "einfacheren" Messfunktionen durchaus möglich sein, sie auf der ganzen Potenzmenge zu definieren. Ein Beispiel ist die Messfunktion über einer Menge , die konstant Null ist.
Mengenringe
BearbeitenWir können also im Allgemeinen nicht hoffen, eine additive Mengenfunktion auf der ganzen Potenzmenge definieren zu können. Das macht es nötig, sich über das Mengensystem, das als Definitionsbereich von Messfunktionen dienen soll, genauer Gedanken zu machen. Wirft man einen Blick in Literatur zur Maßtheorie, findet man dort einen ganzen Zoo an Mengensystemen: Halbringe, Ringe, -Ringe (sprich: "Sigma-Ringe"), Algebren, -Algebren, Dynkin-Systeme, monotone Klassen, ... Eine Übersicht findest du In diesem Artikel
Intuitiv sollte der Definitionsbereich einer additiven (und subadditiven) Messfunktion stabil unter den folgenden Mengenoperationen sein: der disjunkten Vereinigung endlich vieler Mengen und ihrem Gegenstück, dem Bilden von Differenzen von Mengen. Hat man die Differenzoperation zur Verfügung, kann man außerdem beliebige Vereinigungen "künstlich" disjunkt machen: Sind und (nicht notwendigerweise disjunkte) Mengen, so ist , wobei die beiden vereinigten Mengen auf der rechten Seite der Gleichung wieder in liegen. Man kann also die Disjunktheit vergessen und von beliebigen endlichen Vereinigungen sprechen. Um triviale Fälle auszuschließen, fordern wir schließlich noch und können nun definieren:
Definition (Mengenring)
Sei eine Menge. Ein Mengensystem heißt Mengenring (oder kurz Ring), falls gilt:
Hinweis
- Für jeden Ring gilt : Nach Bedingung 1 gibt es mindestens ein Element , und mit 3 gilt auch .
- Mit Induktion folgt aus Punkt 2 die Stabilität des Mengensystems unter beliebigen endlichen Vereinigungen.
Beispiele für Mengenringe
BearbeitenÜber jeder Grundmenge gibt es die beiden Ringe und .
Beispiel (abzählbare Teilmengen)
Das Mengensystem der abzählbaren Teilmengen von ist ein Ring:
- Da die leere Menge abzählbar ist, ist nichtleer.
- Sind zwei abzählbare Mengen, dann ist auch ihre Vereinigung abzählbar, also gilt .
- Sind abzählbar, dann ist wegen auch ihre Differenz abzählbar und es gilt .
Beispiel (endliche Teilmengen)
Das Mengensystem der endlichen Teilmengen von ist ein Ring:
- Die leere Menge ist endlich, also ist nichtleer.
- Sind endlich, dann auch ihre Vereinigung, also ist .
- Sind endlich, dann wegen auch ihre Differenz, also ist .
Ein weiteres wichtiges Beispiel für einen Ring ist das folgende:
Beispiel (Ring der Quaderfiguren)

Betrachte das Mengensystem
der achsenparallelen Quader im . (Die Intervalle im Produkt können offen, halboffen oder abgeschlossen sein.) Der Ring der Quaderfiguren in ist definiert als der von erzeugte Ring, das heißt der kleinste Ring, der enthält. Seine Elemente sind sogenannte Quaderfiguren, d.h. endliche Vereinigungen von achsenparallelen Quadern im . Man kann diesen Ring explizit angeben: Es ist der Durchschnitt aller Mengenringe über , welche die Quader enthalten. (Vergleiche auch den Artikel zu erzeugten -Algebren.)
Inhalte auf Ringen
BearbeitenWir haben nun einige Eigenschaften gefunden, die eine Messfunktion erfüllen sollte, um sinnvoll das Messen einer extensiven Größe zu beschreiben: die Nichtnegativität, Subadditivität (insbesondere Monotonie) und die Additivität. Als natürliche Definitionsbereiche solcher Funktionen haben wir Ringe kennengelernt.
Auf Ringen ist Additivität ausreichend
BearbeitenVorhin haben wir bemerkt, dass aus der Additivität einer Messfunktion im Allgemeinen nicht ihre Subadditivität, nicht einmal ihre Monotonie folgt - jedenfalls nicht, wenn nichts weiter über den Definitionsbereich bekannt ist. Wenn aber das Mengensystem ein Ring ist, folgt die Monotonie und die Subadditivität schon aus der Additivität und Nichtnegativität der Messfunktion. Der Grund dafür ist, dass man aufgrund der Differenzstabilität des Mengensystems Vereinigungen leicht "künstlich" disjunkt machen kann und so die Eigenschaft der Additivität ausnutzen kann. Beim Beweis dieser Aussage ist es geschickt, zuerst die etwas einfachere Eigenschaft der Monotonie und danach die Subadditivität zu zeigen.
Satz (Additive, nichtnegative Mengenfunktionen auf Ringen sind monoton)
Sei ein Ring über der Grundmenge und sei eine additive und nichtnegative Mengenfunktion. Dann gilt: ist monoton.
Beweis (Additive, nichtnegative Mengenfunktionen auf Ringen sind monoton)
Seien mit . Die Idee ist, das "Mehr" von gegenüber zu bestimmen: Da ein Ring ist, ist und es gilt aufgrund der Additivität
wobei wir im letzten Schritt die Nichtnegativität von ausgenutzt haben.
Satz (Additive, nichtnegative Mengenfunktionen auf Ringen sind subadditiv)
Mit den Bezeichnungen des vorherigen Satzes gilt: ist subadditiv.
Beweis (Additive, nichtnegative Mengenfunktionen auf Ringen sind subadditiv)
Seien mit . Wir machen die Vereinigung der "künstlich" disjunkt:
Es entsteht also jedes durch Herausnehmen aller Elemente, die schon in den Mengen enthalten sind. Beachte, dass die ebenfalls im Ring liegen (stabil unter Differenz und Vereinigung).
Damit gilt auch für alle und es folgt aus der Additivität und der schon gezeigten Monotonie von :
Definition
BearbeitenMan kann also die Monotonie und Subadditivität einer auf einem Ring definierten Messfunktion schon allein über ihre Nichtnegativität und Additivität charakterisieren. Damit können wir nun alle Eigenschaften, die eine Messfunktion besitzen sollte, in der folgenden Definition zusammenfassen.
Definition (Inhalt auf einem Ring)
Sei ein Ring über der Menge . Eine nichtnegative Mengenfunktion heißt Inhalt (auf ), falls gilt:
- ,
- ist additiv.
Den Wert einer Menge nennen wir den Inhalt von .
Die Bedingung ist intuitiv sinnvoll und dient außerdem dazu, den pathologischen Fall auszuschließen.
Hinweis
Manchmal werden Inhalte auch auf anderen Mengensystemen definiert, zum Beispiel auf sogenannten Halbringen oder Algebren.
Beispiele
BearbeitenBeispiel
Sei der Ring aller endlichen Teilmengen von und sei die Mengenfunktion
welche die Anzahl der Elemente einer Menge bestimmt. Das ist ein Inhalt:
- Die leere Menge enthält keine Elemente, also ist .
- Seien disjunkt. Wegen der Disjunktheit ist die Anzahl der Elemente in der Vereinigung die Summe der Anzahl der Elemente in und und es gilt .
Man kann diesen Inhalt auch auf der gesamten Potenzmenge betrachten. Dann muss man sich nur überlegen, dass die Additivität auch dann gilt, wenn eine oder beide der disjunkten Mengen unendlich viele Elemente enthalten.
Beispiel
Für eine beliebige Teilmenge definiere
Das ist ein Inhalt auf :
- Die leere Menge ist endlich, also gilt .
- Sind und disjunkt, dann ist , falls die Mengen beide endlich sind. Ist eine der beiden oder beide Mengen unendlich, gilt Additivität ebenfalls: Ist o.E. unendlich, dann ist .
Ein besonders wichtiges Beispiel ist der sogenannte elementargeometrische Inhalt:
Beispiel (Elementargeometrischer Inhalt auf dem Ring der Quaderfiguren)
Wir kennen schon den Ring der Quaderfiguren, dessen Elemente endliche Vereinigungen von achsenparallelen Quadern im sind. (Ein achsenparalleler Quader im ist ein Produkt von Intervallen (jeweils offen, halboffen oder abgeschlossen).) Man kann zeigen, dass sich jede solche Quaderfigur als disjunkte Vereinigung von Quadern schreiben lässt.
Man definiert den elementargeometrischen Inhalt auf folgendermaßen: Für einen Quader definiere als das Produkt der Seitenlängen. Für eine Quaderfigur , d.h. eine (ohne Einschränkung disjunkte) Vereinigung von Quadern definiere als die Summe der elementargeometrischen Volumina der einzelnen Quader.
Man kann zeigen, dass die so definierte Mengenfunktion ein Inhalt auf dem Ring der Quaderfiguren ist. Man muss sich außerdem noch überlegen, dass wohldefiniert ist, dass also der Wert nicht von der gewählten Zerlegung der Quaderfigur in disjunkte Quader abhängt.
Weitere Eigenschaften von Inhalten
BearbeitenWir sammeln Eigenschaften von Inhalten. Im Folgenden sei ein Ring (insbesondere abgeschlossen unter Bildung von Differenzen und endlichen Vereinigungen) und sei ein Inhalt.
Satz (Subtraktivität)
Inhalte sind subtraktiv: Seien mit und . Dann gilt .
Beweis (Subtraktivität)
Wegen der Additivität gilt . Wegen kann man auf beiden Seiten der Gleichung subtrahieren und erhält das Ergebnis.
Warnung
Man kann auf die Bedingung nicht verzichten! Gilt nämlich , erhält man den undefinierten Ausdruck . Es ist nicht klar, was dabei herauskommt. Ist zum Beispiel der elementargeometrische Inhalt auf , der jedem Intervall seine Länge zuordnet, dann ist für der Wert "". Aber für und erhält man "".
Eine weitere Eigenschaft von endlichen Inhalten (d.h. für alle Mengen ) ist das sogenannte Einschluss-Ausschluss-Prinzip. Es ist unter anderem in der Wahrscheinlichkeitstheorie wichtig und führt den Inhalt einer Vereinigung von Mengen auf eine Summe von Inhalten von Schnitten zurück. Beachte: Für einen Ring und gilt auch . Endliche Schnitte von Mengen aus liegen also wieder in .
Satz (Einschluss-Ausschluss-Prinzip)
Sei der Inhalt endlich und seien , . Dann gilt
Beweis (Einschluss-Ausschluss-Prinzip)
Was bedeutet diese Formel überhaupt? Wir machen uns zunächst klar, was sie für kleine bedeutet:
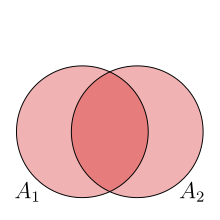
- Für ist
OK, das ist offensichtlich.
- Für ist
Die Formel sagt uns also: wollen wir das Volumen einer Vereinigung berechnen, bietet es sich an, dass wir zunächst die Maße (=Flächeninhalte) von und addieren. Dabei haben wir den Überlapp allerdings "doppelt" gezählt und müssen ihn wieder abziehen.

- Für ist
Ein etwas komplizierterer Fall: Wir addieren, zunächst alle 3 Maße. Dabei wurden die "Zweifach-Überlappflächen" , und doppelt gezählt. Die "Dreifach-Überlappfläche" sogar dreifach! Durch das Abziehen der drei "Zweier-Schnittflächen" wird die Doppelung in den entfernt. Aber das Maß von wurde dreimal abgezogen, sprich einmal zu viel. Wir müssen es also zum Schluss wieder hinzufügen.
Hier zeichnet sich ein Induktion über ab: Der Schritt in lässt sich auf höhere verallgemeinern und als Induktionsanfang nehmen wir einfach .
Aussageform, deren Allgemeingültigkeit für bewiesen werden soll:
1. Induktionsanfang:
Für ist offensichtlich .
2. Induktionsschritt:
2a. Induktionsvoraussetzung:
2b. Induktionsbehauptung:
2c. Beweis des Induktionsschritts:
Im Schritt muss zur Vereinigung auf der linken Seite das Maß hinzugefügt werden - allerdings abzüglich der Mengen, die bereits enthalten sind. Wir haben also

Auf den ersten Term auf der rechten Seite (entspricht den 3 Kreisen in der Abbildung) können wir die Induktionsvoraussetzung anwenden, denn die Vereinigung geht nur bis :
Im dritten Term rechts (entspricht der roten Fläche in der Abbildung) macht es keinen Unterschied, ob wir mit der ganzen Vereinigung schneiden, oder erst alle Mengen einzeln schneiden und dann vereinigen. In beiden Fällen wird aus der Vereinigung "alles außerhalb von herausgeschnitten":
Ersetzen des ersten und dritten Terms rechts ergibt:
Was bedeutet nun der komplizierte Ausdruck auf der rechten Seite? Und entspricht er tatsächlich der Induktionsbehauptung? Die rechte Seite besteht aus 3 Summen, deren Summanden schon einmal die gewünschte Form aus der Induktionsbehauptung haben (inklusive der richtigen Vorzeichen).
- Der erste Term enthält nun alle Summanden, in denen nicht vorkommt.
- Der zweite Term enthält alle Summanden, in denen zwar aber kein anderes vorkommt
- Der dritte Term enthält alle Summanden, in denen und mindestens ein weiteres vorkommt.
Insgesamt haben wir also jeden Summanden aus der Induktionsbehauptung genau einmal abgedeckt. Denn jeder Summand enthält entweder oder nicht und entweder einen der Terme oder nicht. Es ist also
und die Induktionsbehauptung ist bewiesen.








![{\displaystyle [a_{1},b_{1}]\times [a_{2},b_{2}]\times [a_{3},b_{3}]\subseteq \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5322ada035f64bb968be0b1187fa9e9a2bd48268)

![{\displaystyle (a_{i},b_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ddb403df05aa19b9e997798ba95d48a9fa37d6d)








![{\displaystyle [0,\infty ]:=\mathbb {R} _{0}^{+}\cup \{\infty \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7de5951aac33f2684875448f3eef9010e627eb2)

















![{\displaystyle \mu :{\mathcal {C}}\rightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06d2b7a145e4a8689a51cd6eee53f5a81a2a7946)
























![{\displaystyle [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52088d5605716e18068a460dec118214954a68e9)




![{\displaystyle \mu :{\mathcal {P}}(\mathbb {R} ^{n})\rightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45afcc0119aba183bf15e4cab27ad15322386fd)






![{\displaystyle \mu ([0,1]^{n})=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8a6af2484d737fa4a63167a8350a5f571f4923)






























![{\displaystyle \mu :{\mathcal {P}}(\Omega )\supseteq {\mathcal {R}}\rightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a22f3f88e061e20d916c80815c6bfee16ec54c3)












![{\displaystyle \mu :{\mathcal {R}}\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7b11383d04db361504135058e7751dc669c823)


















![{\displaystyle \mu \colon {\mathcal {R}}\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bf1de550ba65db8deccc44e5f6d49e83186aaff)







![{\displaystyle A=(-\infty ,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/854508b0a3aeab8a9e04ac56e77ce140c49be3d9)































