Grenzwert: Konvergenz und Divergenz – Serlo „Mathe für Nicht-Freaks“

In diesem Kapitel wird das Konzept des Grenzwerts (auch Limes genannt) bzw. der Konvergenz einer Folge eingeführt. Da Begriffe wie Stetigkeit, Ableitung und Integral mithilfe des Grenzwertbegriffes definiert werden, ist der Grenzwert sehr wichtig. Er bildet damit das Rückgrat der Analysis.

Intuition hinter der Idee der Konvergenz

Intuition hinter dem Begriff Konvergenz (Youtube-Video von Math-Intuition)

Erklärungsvideo zur Folgenkonvergenz. (YouTube-Video vom Kanal Quatematik)

Um eine mathematische Definition des Grenzwerts zu finden, sollten wir zunächst eine intuitive Idee für diesen Begriff bekommen. Schauen wir uns dafür die harmonische Folge $\left({\tfrac {1}{n}}\right)_{n\in \mathbb {N} }$ an. Sie hat die Folgenglieder

$1,\,{\tfrac {1}{2}},\,{\tfrac {1}{3}},\,{\tfrac {1}{4}},\,{\tfrac {1}{5}},\ldots$

Diese nähern sich von oben immer mehr der Null an und man kann intuitiv sagen:

• Die Folge geht beliebig nah an $0$.
• Je größer $n$ ist, desto mehr nähert sich $a_{n}={\tfrac {1}{n}}$ der $0$ an.
• Die Folge $a_{n}={\tfrac {1}{n}}$ strebt gegen $0$.
• Die Folge $a_{n}={\tfrac {1}{n}}$ erreicht im Unendlichen die $0$.
• …

Alle diese Erklärungen beschreiben intuitiv, was wir in der Analysis den Grenzwert einer Folge nennen. In diesem Fall ist $0$ der Grenzwert der harmonischen Folge $\left({\tfrac {1}{n}}\right)_{n\in \mathbb {N} }$.

Herleitung der Definition des Grenzwerts

Erste Schritte

Um als Mathematiker mit dem Begriff des Grenzwerts arbeiten zu können, brauchen wir eine klare und exakte Definition. Diese können wir finden, indem wir mit einer intuitiven Idee starten und diese so lange konkretisieren, bis wir eine exakte mathematische Definition haben. Die Konkretisierung erfolgt so lange, bis wir eine Formulierung finden, die nur noch bereits definierte Begriffe enthält. Fangen wir mit der folgenden intuitiven Beschreibung des Grenzwerts an:

„Eine Folge hat einen Grenzwert $a$, wenn ihre Folgenglieder beliebig nahe an $a$ gehen.”

Was bedeutet „beliebig nahe“ im obigen Satz? Wir können es so übersetzen: Stellen wir uns die Folgenglieder in einem Koordinatensystem vor, wobei auf der $x$-Achse die Indizes $n$ und auf der $y$-Achse die Werte der Folgenglieder $a_{n}$ stehen. Jedes Folgenglied wird durch einen Punkt in diesem Koordinatensystem dargestellt. Den Grenzwert $a$ veranschaulichen wir durch eine gestrichelte Linie.

Folgenglieder im KOSY

Wenn die Folgenglieder nun „beliebig nahe“ an $a$ herangehen, wird der Abstand zum Grenzwert immer kleiner. Nun nehmen wir einen sehr schmalen „Schlauch“ (man kann es sich wie einen Gartenschlauch vorstellen), der den Radius $\epsilon$ hat. Diesen „fädeln“ wir von rechts über den Grenzwert. Solange der Abstand der Folgenglieder zum Grenzwert kleiner als der Schlauch dick ist, kann man den Schlauch noch weiter nach links schieben. Alle Punkte befinden sich immer noch innerhalb des Schlauches. Sobald ein Punkt aber einen größeren Abstand zum Grenzwert hat, kann er nicht mehr innerhalb des Schlauches liegen. An dieser Stelle müssen wir aufhören, den Schlauch weiter aufzufädeln.

Epsilonschlauch

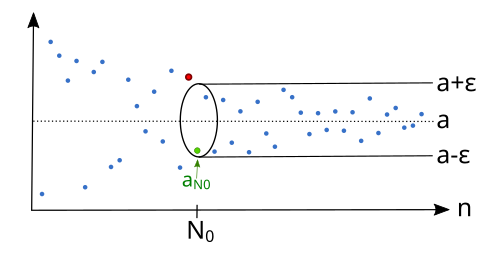
Der Punkt ${\color {forestgreen}a_{N_{0}}}$ ist das Folgenglied, ab dem alle späteren Folgenglieder (also mit Index größer gleich $N_{0}$) innerhalb des Schlauches liegen. Direkt vor $\color {OliveGreen}a_{N_{0}}$ liegt ein Punkt, der außerhalb des Schlauchs liegt. Wenn wir den Schlauch jetzt dünner machen, können vielleicht nicht mehr alle Punkte innerhalb des Schlauches liegen, die vorher im großen Schlauch lagen. Deshalb kann man den dünnen Schlauch nicht mehr so weit nach links schieben, wenn noch alle Punkte innerhalb des Schlauches liegen sollen. Jedoch ist es auch bei ihm möglich, dass fast alle Folgenglieder „eingefangen“ werden können:

Epsilonschlauch klein

Nun ist der Punkt, der nicht mehr in den dünneren Schlauch passt, weiter rechts als im vorherigen Bild. Das neue erste Folgenglied im Schlauch nennen wir ${\color {forestgreen}a_{N_{1}}}$. Alle Folgenglieder mit einem Index größer gleich $N_{1}$ liegen in dem dünneren Schlauch.

Dieser Schlauch hat keine nähere mathematische Bedeutung. Wir haben ihn nur verwendet, um zu zeigen, dass die Folgenglieder immer näher an der gestrichtelten Linie liegen. Sie gehen also immer näher an $a$ heran und insbesondere auch nicht mehr weiter weg, da sie ja ab einem bestimmten Index alle innerhalb des Schlauches liegen, egal wie dünn dieser ist. Haben wir das verstanden, brauchen wir den „Schlauch“ nicht mehr. Was bisher unser beliebig dünner Schlauch mit Radius $\epsilon$ war, werden wir $\epsilon$-Umgebung nennen.

In jeder Umgebung um den Grenzwert liegen fast alle Folgenglieder

Der Grenzwert ist eine Zahl, so dass für jede $\epsilon$-Umgebung fast alle Folgenglieder in dieser Umgebung um die Zahl liegen.

Wir haben Indizes wie $N_{0}$ bzw. $N_{1}$ gefunden, ab denen alle nachfolgenden Folgenglieder innerhalb der jeweiligen $\epsilon$-Schläuche liegen. Machen wir den Schlauch noch dünner, finden wir entsprechend ein $N_{2}$, ab dem alle Folgenglieder im Schlauch liegen und so weiter. Egal wie dünn wir den Schlauch machen, es wird immer einen Punkt geben, ab dem alle weiteren Folgenglieder im Schlauch liegen.

Da solche Startindizes wie $N_{0}$ natürliche Zahlen sind, kann es nur endlich viele Folgenglieder geben, die außerhalb des Schlauches liegen (nämlich höchstens $N_{0}-1$ Folgenglieder). Alle restlichen Folgenglieder liegen innerhalb des Schlauchs. Da eine Folge unendlich viele Folgenglieder hat, kann man die endlich vielen Glieder, die außerhalb liegen, vernachlässigen und sagen, dass fast alle Glieder innerhalb des Schlauches liegen. Das geht selbst, wenn das $N_{0}$ sehr groß ist. Denn in Relation zu unendlich vielen Folgegliedern, die innerhalb des Schlauchs liegen, sind endlich viele Folgeglieder außerhalb des Schlauchs wenig – egal wie groß $N_{0}$ ist. Das zu verstehen ist wichtig, um den Grenzwertbegriff zu verstehen.

Wir haben also herausgefunden, dass fast alle Folgenglieder in dem Schlauch liegen, egal wie dünn dieser ist. Das heißt, dass die Folgenglieder immer näher an den Grenzwert $a$ herangehen. Und das ist es, was den Grenzwert ausmacht. Die Folgenglieder $a_{n}$ liegen beliebig nah am Grenzwert $a$, wenn wir hinreichend große $n$ betrachten.

Was ist eine Umgebung einer Zahl?

Eine Umgebung einer Zahl $a$ lässt sich geometrisch mithilfe eines Kreises konstruieren. Sei dazu $a$ der Mittelpunkt eines Kreises mit dem Radius $0$. Dann ist zunächst der Punkt $a$ eingezeichnet. Erweitert man den Radius dieses Kreises beliebig weit, so vergrößert sich der Durchmesser ausgehend von dem Mittelpunkt $a$.

Wir behaupten: Eine Umgebung ist intuitiv gesprochen eine Menge von Zahlen, welche die Zahl $a$ umschließt.

Im Eindimensionalen ist dieser Kreis nichts anderes als ein offenes Intervall. Eine Umgebung einer Zahl $a$ lässt sich mathematisch auch mithilfe eines solchen Intervalls konstruieren. Der Radius des Kreises entspricht dem Abstand zum linken und rechten Rand des Intervalls. Dieser ist eine beliebige positive Zahl $\epsilon >0$.

Ein solches Intervall ist charakterisiert als die Menge aller Zahlen, die einen Abstand von $a$ kleiner $\epsilon$ besitzen. Damit haben sie die Form $(a-\epsilon ,a+\epsilon )$.

Man nennt dieses Intervall auch $\epsilon$-Umgebung von $a$, die so aussieht:

Die Epsilon-Umgebung

Eine solche $\epsilon$-Umgebung von $a$ definiert allgemein die Umgebung einer Zahl $a$. Eine Menge $M$ ist dadurch eine Umgebung von $a$, wenn es eine $\epsilon$-Umgebung $(a-\epsilon ,a+\epsilon )$ gibt, so dass $(a-\epsilon ,a+\epsilon )\;\subseteq M$ ist. Wir betrachten beispielsweise die folgende Menge $M$:

Menge M mit inneren Punkt a auf der Zahlengeraden

Zunächst finden wir die $\epsilon$-Umgebung von $a$. Dazu wählen wir ein beliebiges $\epsilon >0$ und legen einen Kreis um $a$. Genauer gesagt finden wir ein Intervall $(a-\epsilon ,a+\epsilon )$. Die Menge $M$ ist ebenfalls eine Menge von Zahlen und somit ein Intervall im Eindimensionalen. Diese umschließt das Intervall $(a-\epsilon ,a+\epsilon )$. Sie ist also eine Obermenge der $\epsilon$-Umgebung von $a$. Deswegen ist $M$ auch eine Umgebung von $a$.

Menge M mit inneren Punkt a und ε-Umgebung um a

Definition (Umgebung)

Eine Menge $U$ ist eine Umgebung der Zahl $a$, wenn es ein $\epsilon >0$ gibt, so dass $(a-\epsilon ,a+\epsilon )\;\subseteq U$ ist.

Was bedeutet „fast alle“?

Dazu stellen wir uns ein Koordinatensystem vor, auf dem unendlich viele Folgenglieder einer konvergierenden Folge dargestellt sind. Nun nehmen wir einen $\epsilon$-Schlauch und fädeln ihn von rechts über den Grenzwert ein. Dann passt eine endliche Anzahl an Folgengliedern nicht in den Schlauch, weil der Abstand zum Grenzwert $a$ nicht klein genug ist. Jedoch liegen unendlich viele Folgenglieder innerhalb des Intervalls $(a-\epsilon ,a+\epsilon )$ und damit im $\epsilon$-Schlauch.

Die Anzahl der Folgenglieder, die innerhalb des Intervalls $(a-\epsilon ,a+\epsilon )$ liegen, ist also überwältigend groß im Vergleich zur Anzahl der Folgenglieder außerhalb dieses Intervalls. Man sagt daher, dass fast alle Folgenglieder im Intervall $(a-\epsilon ,a+\epsilon )$ liegen.

Wenn „fast alle“ Folgenglieder im Intervall $(a-\epsilon ,a+\epsilon )$ liegen, so bedeutet es, dass „alle bis auf endlich viele“ Folgenglieder ein Element dieses Intervalls sind.

Verfeinerung der mathematischen Definition

Insgesamt können wir definieren:

„Eine Folge hat einen Grenzwert $a$, wenn es für jede $\epsilon$-Umgebung von $a$, also $]a-\epsilon ,a+\epsilon [$, ein Folgenglied gibt, ab dem alle folgenden Folgenglieder Elemente der Umgebung sind.“

Obige Aussage könnten wir als mathematische Definition des Grenzwerts verwenden. Jedoch ist es sinnvoll, diese Definition noch weiter zu formalisieren.

Nun ist ein Folgenglied $a_{n}$ genau dann ein Element von $(a-\epsilon ,a+\epsilon )$, wenn $|a_{n}-a|<\epsilon$ ist. Also:

„Eine Folge $\left(a_{n}\right)_{n\in \mathbb {N} }$ hat einen Grenzwert $a$, wenn es zu jedem $\epsilon >0$ ein Folgenglied $a_{N}$ gibt, ab dem für alle folgenden Folgenglieder $a_{n}$ die Ungleichung $|a_{n}-a|<\epsilon$ erfüllt ist.

Den Teil „es gibt ein Folgenglied, ab dem gilt …“ können wir umformulieren zu „es gibt eine natürliche Zahl $N$, so dass für alle $a_{n}$ mit $n\geq N$ gilt …“. Somit:

„Eine Folge $\left(a_{n}\right)_{n\in \mathbb {N} }$ hat einen Grenzwert $a$, wenn es zu jedem $\epsilon >0$ eine natürliche Zahl $N$ gibt, so dass $|a_{n}-a|<\epsilon$ für alle $n\geq N$ ist.

Dies ist dann auch die mathematische Definition des Grenzwerts.

Definition des Grenzwerts

Definition (Grenzwert)

Eine Folge $\left(a_{n}\right)_{n\in \mathbb {N} }$ besitzt einen Grenzwert $a$, wenn es zu jedem $\epsilon >0$ einen Folgenindex $N\in \mathbb {N}$ gibt, so dass für alle Folgenglieder $a_{n}$ mit $n\geq N$ die Ungleichung $|a_{n}-a|<\epsilon$ erfüllt ist. Es ist also genau dann $a$ ein Grenzwert von $\left(a_{n}\right)_{n\in \mathbb {N} }$, wenn gilt:

$\forall \epsilon >0\,\exists N\in \mathbb {N} \,\forall n\geq N:|a_{n}-a|<\epsilon$

Kommentiert lautet die prädikatenlogische Definition des Grenzwerts:

${\begin{array}{l}\underbrace {{\underset {}{}}\forall \epsilon >0:} _{{\text{Zu jeder Schranke }}\epsilon >0}\ \underbrace {{\underset {}{}}\exists N\in \mathbb {N} :} _{{\text{ existiert ein Index }}N}\ \underbrace {{\underset {}{}}\forall n\geq N:} _{{\text{so dass für alle Indizes }}n\geq N}\\[1em]\quad \quad \underbrace {{\underset {}{}}|a_{n}-a|<\epsilon } _{{\text{ der Abstand von }}a_{n}{\text{ zu }}a{\text{ kleiner als }}\epsilon {\text{ ist}}}\end{array}}$

Es folgen einige Definitionen im Zusammenhang mit dem Grenzwert:

Konvergenz

Eine Folge heißt konvergent, wenn sie einen Grenzwert besitzt. Man sagt auch, dass eine Folge gegen $a$ konvergiert, wenn sie den Grenzwert $a$ besitzt.

Divergenz

Eine Folge nennt man divergent, wenn sie keinen Grenzwert besitzt.

Nullfolge

Eine Nullfolge ist eine konvergente Folge mit dem Grenzwert $0$.

Wenn eine Folge gegen $a$ konvergiert, schreibt man $\lim _{n\to \infty }a_{n}=a$ oder „$a_{n}\rightarrow a$ für $n\rightarrow \infty$“. Man spricht hier „Limes von $a_{n}$ für $n$ gegen unendlich ist $a$“.

Frage: Wie lautet die Aussage in Prädikatenlogik dafür, dass eine Folge $(a_{n})_{n\in \mathbb {N} }$ konvergiert?

Wie oben besprochen, ist die Aussage dafür, dass eine Folge $(a_{n})_{n\in \mathbb {N} }$ den Grenzwert $a$ besitzt, folgende:

$\forall \epsilon >0\,\exists N\in \mathbb {N} \,\forall n\geq N:|a_{n}-a|<\epsilon$

Wenn man nur die Konvergenz haben will, dann ist die Aussage entsprechend:

$\exists a\in \mathbb {R} \,\forall \epsilon >0\,\exists N\in \mathbb {N} \,\forall n\geq N:|a_{n}-a|<\epsilon$

Frage: Wie lautet die Aussage in Prädikatenlogik dafür, dass eine Folge $(a_{n})_{n\in \mathbb {N} }$ divergiert?

Hierzu muss obige gefundene Aussage negiert werden. Es werden dabei All- zu Existenzquantoren und umgekehrt. Die negierte Aussage lautet:

$\forall a\in \mathbb {R} \,\exists \epsilon >0\,\forall N\in \mathbb {N} \,\exists n\geq N:|a_{n}-a|\geq \epsilon$

In Worten: Zu jedem $a\in \mathbb {R}$ gibt es eine reelle Zahl $\epsilon >0$, so dass es für alle $N\in \mathbb {N}$ ein $n\geq N$ mit $|a_{n}-a|\geq \epsilon$ gibt.

Hinweis

Für den Betrag gilt $|-x|=|x|$. Dementsprechend ist

$|a_{n}-a|=|-(a-a_{n})|=|a-a_{n}|$

Es ist also egal, ob wir $|a_{n}-a|$ oder $|a-a_{n}|$ in der Definition verwenden.

Hinweis

Aus der Definition der Konvergenz folgt unmittelbar, dass $(a_{n})_{n\in \mathbb {N} }$ genau dann gegen $a$ konvergiert, wenn $(|a_{n}-a|)_{n\in \mathbb {N} }$ eine Nullfolge ist. Wenn nämlich $(|a_{n}-a|)_{n\in \mathbb {N} }$ gegen $0$ konvergiert, dann ist per Definition

$\forall \epsilon >0\,\exists N\in \mathbb {N} \,\forall n\geq N:||a_{n}-a|-0|=||a_{n}-a||=|a_{n}-a|<\epsilon$

Dies entspricht aber der Definition dafür, dass $(a_{n})_{n\in \mathbb {N} }$ gegen $a$ konvergiert. Konvergiert umgekehrt $(a_{n})_{n\in \mathbb {N} }$ gegen $a$, so gilt per Definition

$\forall \epsilon >0\,\exists N\in \mathbb {N} \,\forall n\geq N:|a_{n}-a|<\epsilon$

Somit gilt auch $||a_{n}-a|-0|=||a_{n}-a||=|a_{n}-a|<\epsilon$ mit gleichen Quantoren und gleicher Variablendeklaration, also konvergiert $(|a_{n}-a|)_{n\in \mathbb {N} }$ gegen $0$

Warnung

Im Studium begegnet man hin und wieder der Fehlvorstellung „Eine Folge divergiert genau dann, wenn sie unbeschränkt ist.“ Diese Aussage ist falsch!

Der intuitive Denkfehler dahinter ist wahrscheinlich oft der voreilige Schluss: „Das Gegenteil von $\forall \epsilon >0\ldots |a_{n}-a|<\epsilon$ ist $\forall \epsilon >0\ \ldots \ |a_{n}-a|\geq \epsilon$, also muss $(a_{n})_{n\in \mathbb {N} }$ beliebig groß werden.“ Dies entspricht aber nicht der hergeleiteten Definition für Divergenz von oben!

Zwar ist jede unbeschränkte Folge divergent (siehe hierzu das Kapitel „Unbeschränkte Folgen divergieren“), aber nicht jede divergente Folge muss zwangsläufig unbeschränkt sein. Ein Beispiel hierfür ist die Folge $\left((-1)^{n}\right)_{n\in \mathbb {N} }=(-1,1,-1,1,-1,1,\ldots )$, welche beschränkt und divergent ist.

Erklärung der Konvergenz

Neben der obigen Herleitung gibt es eine weitere Intuition für den Grenzwertbegriff: Die Größe $|a_{n}-a|$ ist der Abstand zwischen dem n-ten Folgenglied und $a$. Sie ist ein Maß für den Fehler bzw. Unterschied zwischen $a_{n}$ und $a$. Die Ungleichung $|a_{n}-a|<\epsilon$ bedeutet also, dass der Fehler zwischen $a_{n}$ und $a$ garantiert kleiner als der Maximalfehler $\epsilon$ ist. Damit kann die Definition des Grenzwerts folgendermaßen gedeutet werden: Egal was für einen Maximalfehler $\epsilon >0$ man vorgibt, fast alle Folgenglieder haben einen Unterschied kleiner als $\epsilon$ vom Grenzwert $a$. Der Fehler $|a_{n}-a|$ zwischen den Folgengliedern und dem Grenzwert wird also beliebig klein.

Diese Interpretation kann auch durch die Wahl der Variablen gestützt werden. Augustin-Louis Cauchy, auf den obige Definition zurückgeht, könnte mit $\epsilon$ das französische Wort „erreur“ für „Fehler“ gemeint haben.

Beispiel: Konvergenz der harmonischen Folge

Die ersten zehn Folgenglieder der harmonischen Folge

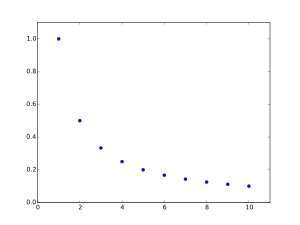
Schauen wir uns das Ganze bei der harmonischen Folge mit dem allgemeinen Glied $a_{n}={\tfrac {1}{n}}$ an. Diese konvergiert intuitiv gesehen gegen $0$. Sie müsste also auch die obige Definition für Konvergenz gegen $0$ erfüllen.

Nimm zum Beispiel $\epsilon ={\tfrac {1}{2}}$. Ab dem dritten Folgenglied $a_{3}={\tfrac {1}{3}}$ ist der Abstand von $a_{n}$ zu $0$ kleiner als $\epsilon ={\tfrac {1}{2}}$. Damit liegen ab dem dritten Folgenglied alle weiteren Folgenglieder in der $\epsilon$-Umgebung $]-{\tfrac {1}{2}},{\tfrac {1}{2}}[$. Für $\epsilon ={\tfrac {1}{10}}$ ist der Abstand der Folge zu $0$ ab $n=11$ und für $\epsilon =0,00001$ ab $n=100001$ kleiner als das jeweils gewählte $\epsilon$.

Machen wir das nun ganz allgemein und denken uns ein beliebiges $\epsilon >0$. Aus dem archimedischen Axiom folgt, dass es ein $N\in \mathbb {N}$ gibt, so dass ${\tfrac {1}{n}}<\epsilon$ für alle $n\geq N$ ist. (Siehe Archimedisches Axiom mit der Wahl von $x=1$ und $y={\frac {2}{\epsilon }}$.) Ab diesem $N$ liegen alle folgenden Folgenglieder in der $\epsilon$-Umgebung $]-\epsilon ,\epsilon [$. Dementsprechend ist der Grenzwert der harmonischen Folge gleich $0$.

Der Grenzwert ist eindeutig

Satz (Eindeutigkeit des Grenzwerts)

Jede konvergente Folge besitzt nur einen einzigen Grenzwert.

Dieser Satz macht Ausdrücke wie $\lim _{n\to \infty }a_{n}$ erst sinnvoll. Stell dir vor, es gäbe eine Folge $\left(b_{n}\right)_{n\in \mathbb {N} }$ mit mehr als einem Grenzwert. Dann könntest du dem Ausdruck $\lim _{n\to \infty }b_{n}$ keine eindeutige Zahl zuordnen, weil du nicht weißt, welchen der Grenzwerte $\lim _{n\rightarrow \infty }b_{n}$ bezeichnen soll. Weil nun aber $\left(b_{n}\right)_{n\in \mathbb {N} }$ maximal einen Grenzwert besitzt, ist stets klar, dass $\lim _{n\to \infty }b_{n}$ diesen eindeutigen Grenzwert bezeichnen soll (unter der Voraussetzung natürlich, dass $\left(b_{n}\right)_{n\in \mathbb {N} }$ konvergiert). Dank des obigen Satzes kann man von „dem Grenzwert“ und nicht nur von „einem Grenzwert“ sprechen.

Wie kommt man auf den Beweis? (Eindeutigkeit des Grenzwerts)

Den Satz werden wir indirekt über einen Widerspruchsbeweis zeigen. Hierzu gehen wir davon aus, dass es eine konvergente Folge $\left(a_{n}\right)_{n\in \mathbb {N} }$ mit zwei verschiedenen Grenzwerten gibt. Diese Annahme müssen wir nun zum Widerspruch führen.

Nennen wir die beiden Grenzwerte $a$ und $b$. Um den Widerspruch zu finden, können wir folgende Methode verwenden: Wir können versuchen, den Gegensatz von dem, was wir eigentlich zeigen wollen, zu beweisen. Dieser Versuch ist natürlich zum Scheitern verurteilt. Wenn wir aber verstehen, warum der Versuch scheitert, dann gibt uns das Hinweise, wie wir den eigentlichen Beweis zu führen haben. Versuchen wir also zu beweisen, dass es eine Folge mit zwei verschiedenen Grenzwerten gibt.

Nimm also ein Blatt Papier und zeichne eine Zahlengerade ein. Markiere nun zwei verschiedene Zahlen auf der Zahlengerade, die unsere zwei Grenzwerte $a$ und $b$ darstellen sollen. Versuche nun eine reelle Folge auf der Zahlengeraden zu finden, die gleichzeitig gegen beide Zahlen konvergiert (Denk daran, dass deine Zahlenfolge ab einem bestimmten Folgenglied in jeder noch so kleinen Umgebung um $a$ beziehungsweise um $b$ sein muss). Für Umgebungen von $a$ und $b$, welche sich nicht überlappen, ist es unmöglich, dass sich dort fast alle Folgenglieder befinden. Die folgende Zeichnung verdeutlicht das Problem.

Zahlengerade mit zwei Zahlen und disjunkten ε-Umgebungen

Wenn man also $\epsilon$ so klein wählt, dass sich $]a-\epsilon ,a+\epsilon [$ und $]b-\epsilon ,b+\epsilon [$ nicht überschneiden, dann sollte sich ein Widerspruch ergeben. Wir wählen $\epsilon ={\tfrac {|a-b|}{3}}$. Wir wissen, dass es ein $a_{n}$ geben muss, welches sowohl in $]a-\epsilon ,a+\epsilon [$ als auch $]b-\epsilon ,b+\epsilon [$ liegt. Ein solches $a_{n}$ kann es aber nicht geben, weil sich die beiden Umgebungen für $\epsilon ={\tfrac {|a-b|}{3}}$ nicht überschneiden. Einen Widerspruch erhalten wir dann über die Dreiecksungleichung:

${\begin{aligned}|a-b|&=|a+\overbrace {(-a_{n}+a_{n})} ^{=0}-b|\\[1ex]&=|(a-a_{n})+(a_{n}-b)|\\[1ex]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Dreiecksungleichung}}\right.}\\[1ex]&\leq |a-a_{n}|+|a_{n}-b|\\[1ex]&<{\frac {|a-b|}{3}}+{\frac {|a-b|}{3}}\\[1ex]&={\frac {2\cdot |a-b|}{3}}\end{aligned}}$

Nach Kürzung beider Seiten mit $|a-b|$ haben wir den Widerspruch $1<{\tfrac {2}{3}}$.

Beweis (Eindeutigkeit des Grenzwerts)

Widerspruchsbeweis: Sei $\left(a_{n}\right)_{n\in \mathbb {N} }$ eine Folge mit mindestens zwei verschiedenen Grenzwerten $a$ und $b$ . Damit ist $|a-b|>0$. Per Definition des Grenzwertes gibt es zwei natürliche Zahlen $N_{1}$ und $N_{2}$ mit

$\forall n\geq N_{1}:\ |a_{n}-a|<{\frac {|a-b|}{3}}$

und

$\forall n\geq N_{2}:\ |a_{n}-b|<{\frac {|a-b|}{3}}$

Dies folgt aus der Definition des Grenzwerts mit $\epsilon ={\tfrac {|a-b|}{3}}$. Damit gilt für alle Folgenglieder $a_{n}$ mit $n\geq \mathrm {max} \{N_{1},\,N_{2}\}$, dass gleichzeitig $|a_{n}-a|<{\tfrac {|a-b|}{3}}$ und $|a_{n}-b|<{\tfrac {|a-b|}{3}}$ ist. In diesem Fall wäre also

${\begin{aligned}|a-b|&=|a+(-a_{n}+a_{n})-b|\\[1ex]&=|(a-a_{n})+(a_{n}-b)|\\[1ex]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Dreiecksungleichung}}\right.}\\[1ex]&\leq |a-a_{n}|+|a_{n}-b|\\[1ex]&<{\frac {|a-b|}{3}}+{\frac {|a-b|}{3}}\\[1ex]&={\frac {2\cdot |a-b|}{3}}\end{aligned}}$

Wegen $a\neq b$ ist $|a-b|>0$ und wir können beide Seiten der obigen Ungleichung durch $|a-b|$ dividieren. So erhalten wir den Widerspruch

$1<{\frac {2}{3}}$

Beachte, wie wichtig es für den Beweis ist, dass $a\neq b$ und damit $|a-b|>0$ ist. Sonst hätten wir nicht beide Seiten durch $|a-b|$ dividieren können und wir hätten nicht $\epsilon ={\tfrac {|a-b|}{3}}>0$ wählen können.