Russells Antinomie und Klassen – Serlo „Mathe für Nicht-Freaks“

Du wirst dich vielleicht schon gewundert haben, warum wir die Cantorsche Mengendefinition „naiv“ genannt haben. Auf den ersten Blick sieht die Definition gut aus und bisher sind keine Probleme aufgetreten. Was sollte also schiefgehen? In diesem Artikel werden wir Russells Antinomie kennen lernen und wie diese über Klassen gelöst werden kann.

Russells Antinomie

Ein Beispiel ist Russells Antinomie, die Bertrand Russell 1903 publizierte:

Beispiel (Russellsche Antinomie)

${\mathcal {R}}$ sei die Menge aller Mengen, die sich nicht selbst enthalten:

${\mathcal {R}}:=\{x\,|\,x\notin x\rbrace$

Dann ist ${\mathcal {R}}$ keine sinnvolle Menge.

Frage: Wieso definiert ${\mathcal {R}}=\{x\,|\,x\notin x\}$ keine sinnvolle Menge?

Stelle dir vor, es gäbe eine Menge ${\mathcal {R}}$, die alle Mengen enthält, die sich nicht selbst enthalten. Ist dann ${\mathcal {R}}\in {\mathcal {R}}$?

Wäre ${\mathcal {R}}$ ein Element von sich selbst, dann muss ${\mathcal {R}}$ die definierende Bedingung $x\notin x$, erfüllen, also ist ${\mathcal {R}}$ doch kein Element von sich selbst   ↯.

Ist ${\mathcal {R}}\notin {\mathcal {R}}$, dann ist nach Definition von ${\mathcal {R}}$ gerade ${\mathcal {R}}\in {\mathcal {R}}$   ↯.

Wir erhalten also sowohl für ${\mathcal {R}}\in {\mathcal {R}}$ als auch für ${\mathcal {R}}\notin {\mathcal {R}}$ einen Widerspruch. Damit kann ${\mathcal {R}}$ keine sinnvolle Menge sein.

Bereits Cantor kannte ähnliche Antinomien. Er glaubte aber nicht, dass seine Definition geändert werden müsse. Er unterteilte hierzu Mengen in konsistente Vielheiten, bei denen eine Zusammenfassung zu einem Ganzen möglich ist und in inkonsistente Vielheiten, bei denen dies nicht der Fall ist. Da in Cantors Mengendefinition ausdrücklich von „Zusammenfassungen zu einem Ganzen“ die Rede ist, werden laut Cantor Mengenausdrücke ausgeschlossen, die nicht sinnvoll eine Menge definieren. Bertrand Russell kleidete die nach ihm benannte Antinomie im Übrigen in folgende Form:

Der Dorfbarbier ist derjenige, der alle Männer im Dorf rasiert, die sich nicht selbst rasieren. Frage: Rasiert der Dorfbarbier sich selbst?

Hier ergibt sich auf den erstem Blick ein ähnlicher Widerspruch, jedoch kann eine einfache Antwort gefunden werden: Der Dorfbarbier ist eine Frau! Diese Antwort hilft uns aus dem Dilemma. Völlig egal ob sie sich nun selbst rasiert oder nicht, entscheidend ist, dass sie kein Mann des Dorfs ist und die obige Aussage kann erfüllt werden.

Wie lösen wir diesen Widerspruch der Russellschen Antinomie? Formal kann die Argumentation dahinter folgendermaßen dargestellt werden:

1. Allgemein gilt:   $\forall x:(x\in {\mathcal {R}}\iff x\notin x)$
2. Setzen wir ${\mathcal {R}}$ für $x$ ein, folgt:   ${\mathcal {R}}\in {\mathcal {R}}\iff {\mathcal {R}}\notin {\mathcal {R}}$
3. Widerspruch:   ↯

Und nun sehen wir genau, wo das Problem entsteht: im zweiten Schritt setzen wir für $x$ die Russellsche Klasse ${\mathcal {R}}$ ein. Dürfen wir das? Die Antwort ist Nein, das dürfen wir nicht! Die Variable $x$ steht für Objekte aus unserem Grundbereich. Das gilt sowohl für das $\color {red}x$ in der Definition der Russellschen Klasse $\{{\color {red}x}\,|\,x\notin x\}$ als auch für das $\color {red}x$ in der Allaussage $\forall {\color {red}x}:x\in {\mathcal {R}}\iff x\notin x$. Die Einsetzung für $x$ ist nur dann erlaubt, wenn das Objekt, das wir für $x$ einsetzen, zum Grundbereich gehört.

Damit finden wir die Lösung zur Russellschen Antinomie. Wir fordern, dass ${\mathcal {R}}=\{x\,|\,x\notin x\}$ nicht zum Grundbereich gehört – genau so wie im obigen Beispiel der Barbier nicht zu den Männern des Dorfes gehört. Wir fordern also, dass ${\mathcal {R}}=\{x\,|\,x\notin x\}$ keine Menge ist. Vielmehr führen wir hierfür ein neues Konzept ein: Wir nennen ${\mathcal {R}}=\{x\,|\,x\notin x\}$ eine Klasse.

Definition (Russelsche Klasse)

${\mathcal {R}}:=\{x\,|\,x\notin x\}$

Klassen sind generell alle Ausdrücke der Form $\{x\,|\,A(x)\}$. Wie wir gesehen haben, können nicht alle diese Ausdrücke sinnvoll eine Menge beschreiben. Wenn dies möglich ist, dann ist die Klasse $\{x\,|\,A(x)\}$ eine Menge und wenn nicht – wie im Fall der Russell-Klasse ${\mathcal {R}}=\{x\,|\,x\notin x\}$ – erhalten wir eine echte Klasse. Um alle Mengen zu bezeichen, definieren wir die Allklasse ${\mathcal {V}}$:

Definition (Allklasse)

${\mathcal {V}}:=\{x\,|\,x=x\}$

${\mathcal {V}}$ steht für unseren Grundbereich, wir dürfen also ${\mathcal {R}}$ nur dann für die Variable $x$ einsetzen, wenn $\color {red}{\mathcal {R}}\in {\mathcal {V}}$ gilt. Mit dieser Voraussetzung sieht die korrekte Argumentation dann so aus:

1. Allgemein gilt:   $\forall x:(x\in {\mathcal {R}}\iff x\notin x)$
2. Setzen wir ${\mathcal {R}}$ für $x$ ein, folgt:   ${\color {red}{\mathcal {R}}\in {\mathcal {V}}}\implies ({\mathcal {R}}\in {\mathcal {R}}\iff {\mathcal {R}}\notin {\mathcal {R}})$
3. Logische Folgerung für $\implies$: ${\mathcal {R}}\notin {\mathcal {V}}$

Die Russelsche Klasse ${\mathcal {R}}$ kann also nicht zum Grundbereich ${\mathcal {V}}$ gehören! Russell entwickelte zur Lösung des Problems von 1903 bis 1908 eine Typentheorie, in der die Klassenbildung stark eingeschränkt wurde. In der Mathematik hat sich aber ein freizügiger Gebrauch von $\{x\,|\,\dotsm \}$ durchgesetzt. Das ist möglich, wenn zwischen Klassen und Mengen unterschieden wird.

Klassen

Die Russellsche Antinomie lehrt, dass die Operation $\{x\,|\,\dotsm \}$ aus dem Variablenbereich hinausführen kann! Das ist beispielsweise bei der Subtraktion auf den natürlichen Zahlen genauso. Sind $a$ und $b$ zwei natürliche Zahlen, so ist die Differenz $(a-b)$ keineswegs immer eine natürliche Zahl. Vielmehr liefert die Differenz neue Objekte. Die neuen Objekte, die durch die Subtraktion von natürlichen Zahlen gebildet werden können, sind die negativen ganzen Zahlen.

Ähnlich verhält es sich mit der Operation $\{x\,|\,\dotsm \}$. Diese führt zu Objekten, die keine Mengen sind. Die Objekte, die mit $\{x\,|\,\dotsm \}$ erzeugt werden können, werden „Klassen“ genannt:

Definition (Klasse)

Eine Klasse ist ein Objekt der Form $\{x\,|\,A(x)\}$, wobei $A(x)$ eine Aussageform ist.

Die Elemente der Klasse $\{x\,|\,A(x)\}$ sind genau die Objekte $y$, die die Formel $A(y)$ erfüllen. Gilt $A(y)$ für ein Objekt $y$ nicht, so ist $y$ kein Element von $\{x\,|\,A(x)\}$. Je nachdem ob $A(y)$ zutriffe oder nicht, gilt $y\in \{x\,|\,A(x)\}$ oder $y\notin \{x\,|\,A(x)\}$. Dieser Zusammenhang zwischen der Klassenbildung $\{x\,|\,\dotsm \}$ und der Elementrelation $\in$ wird Abstraktionsprinzip genannt:

Abstraktionsprinzip: $\forall y:\left(y\in \{x\,\vert A\left(x\right)\}\iff A\left(y\right)\right)$

Es definiert die Klassenbildung, wie wir jetzt – vorsichtig geworden! – anstelle von Mengenbildung sagen. Das Abstraktionsprinzip wurde bereits im Kapitel Mengenschreibweisen beschrieben. Und natürlich gilt es auch für Mengen!

Mengen sind spezielle Klassen und alles, was wir bisher über Mengen gesagt haben, gilt auch für Klassen. Klassen, die keine Mengen sind, werden echte Klassen genannt. Russels Antinomie lehrt also, dass es echte Klassen gibt. Mit der Unterscheidung zwischen Klassen und Mengen konnten wir die Russellsche Antinomie auflösen. Der entscheidende Unterschied zwischen Mengen und Klassen liegt darin, dass Mengen als mögliche Werte für Variable auftreten können, echte Klassen dagegen nicht.

Aber was macht uns sicher, dass mit der Unterscheidung von Mengen und Klassen die Probleme der naiven Mengenlehre behoben sind? Können nicht irgendwelche Widersprüche an anderer Stelle auftreten?

Minimales Modell für die Klassen

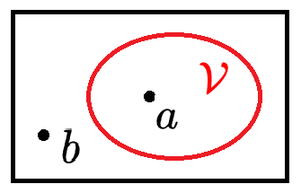
Dazu betrachten wir ein ganz einfaches Modell der Klassenbildung $\{x\,|\,\dotsm \}$ und der Elementrelation $\in$. Der Variablenereich ${\mathcal {V}}$ hat nur ein einziges Element $a$. Es gibt ein weiteres Objekt $b$, dass ausserhalb von ${\mathcal {V}}$ liegt. Weitere Objekte gibt es nicht. Der einelementige Bereich ${\mathcal {V}}$ hat genau zwei Teilklassen: die leere Klasse $\varnothing$ und die Klasse ${\mathcal {V}}$.

Definition (Leere Klasse)

$\varnothing :=\{x\,|\,x\neq x\}$

Für die Elementrelation $\in$ gibt es dann zwei Möglichkeiten:

Verständnisaufgabe: Welche Beziehungen mit $=$ und $\in$ gelten in den beiden Fällen zwischen $a$, $b$, $\varnothing$, ${\mathcal {V}}$ und ${\mathcal {R}}$?

1. $a\notin a$
2. $a\in a$

Lösungen:

1. Ist   $a\notin a$   so ist   a = $\varnothing$   und   $a\in b$ = $\{a\}$ = ${\mathcal {V}}$ = ${\mathcal {R}}$.
2. Ist   $a\in a$   so ist   a = $\{a\}$ = ${\mathcal {V}}$   und   $a\notin b$ = $\varnothing$ = ${\mathcal {R}}$.

Die beiden Modelle für $\{x\,|\,\dotsm \}$ zeigen, dass wir von keiner Klasse erwarten können, dass sie eine Menge ist, das heißt, dass sie im Variablenbereich liegt. Im ersten Modell ist die Allklasse ${\mathcal {V}}$ eine echte Klasse und die leere Klasse $\varnothing$ eine Menge. Im zweiten Modell ist es gerade umgekehrt.

Viele Teile der Mathematik kommen mit der hier vorgestellten naiven Mengenlehre (die genauer Klassenlehre heißen sollte, wie wir jetzt wissen) aus. Doch für viele andere Teile der Mathematik werden Mengen benötigt oder sind zumindest hilfreich. Die Existenz von Mengen wird durch Axiome gewährleistet, die sicherstellen, dass bestimmte Klassen Mengen sind. Solche Axiome werden wir im nächsten Abschnitt vorstellen.

Zuvor wollen wir die formale Sprache genauer festlegen, die wir hier verwenden. Das ist deshalb wichtig, weil die Klassenbildung $\{x\,|\,A(x)\}$ davon abhängt, welche Aussageformen $A(x)$ wir zur Verfügung haben.

Wir legen eine Sprache zu Grunde, die folgendes enthält:

• die Variablen $x,y,z,\dotsc$
• die Junktoren $\neg ,\land ,\lor ,\implies ,\iff$
• die Quantoren $\forall ,\exists$
• die Klassenbildung $\{\;|\;\}$
• die Relationen $=,\in$

Aussagenformen bezeichnen wir mit $A(x),B(y),C(z),\dots$ und Klassen mit ${\mathcal {M}},{\mathcal {N}},{\mathcal {K}},\dots$. Die Russelsche Klasse ${\mathcal {R}}:=\{x\,|\,x\in x\}$, die Allklasse ${\mathcal {V}}:=\{x\,|\,x=x\}$ und die leere Klasse $\varnothing :=\{x\,|\,x\neq x\}$ haben wir bereits definiert. In der Literatur werden Sprachen, die die Klassenbildung erlauben, Klassenlogik genannt.

Hinweis

Wir nennen die Klasse ${\mathcal {K}}$ dann eine Menge, wenn sie im Variblenbereich, also in der Allklasse liegt: ${\mathcal {K}}\in {\mathcal {V}}$.