Lipschitz-Stetigkeit – Serlo „Mathe für Nicht-Freaks“
Die Lipschitz-Stetigkeit ist eine Verschärfung der Stetigkeit. Sie ist noch strenger als die gleichmäßige Stetigkeit und wird in der Theorie der Differentialgleichungen häufig verwendet.
Herleitung
BearbeitenWir werden mit der Definition der Lipschitz-Stetigkeit noch einen weiteren Stetigkeitsbegriff kennenlernen, der uns Genaueres über das Änderungsverhalten einer Funktion verrät. Bekanntlich führen bei stetigen Funktionen hinreichend kleine Änderungen des Arguments zu beliebig kleinen Änderungen des Funktionswerts. Bei Lipschitz-stetigen Funktionen ist es darüber hinaus möglich, den Betrag der Änderung der Funktion abzuschätzen. Es kann also eine Aussage darüber getroffen werden, wie „schnell“ die Abweichungen der Funktionswerte klein werden. Um das besser zu verstehen, betrachten wir zunächst, was mit der Änderung einer Funktion gemeint ist. Sei hierzu eine beliebige Funktion mit dem Definitionsbereich .
Nehmen wir zwei beliebige Punkte und aus dem Definitionsbereich einer Funktion und legen wir eine Gerade durch die beiden zugehörigen Funktionswerte und . Anschaulich ist klar, dass die Gerade umso steiler verlaufen muss, je größer die Differenz von und ist. Die durchschnittliche Änderung zwischen zwei Funktionswerten entspricht der Steigung der durch die beiden Punkte verlaufenden Sekanten und kann wie gewohnt mit einem Steigungsdreieck berechnet werden:

Nehmen wir nun an, die Änderung einer Funktion ist beschränkt, d. h. die Steigungen der Sekanten werden nicht beliebig groß oder klein. Der Betrag besitzt also eine obere Schranke. Durch die Betragsstriche werden sowohl positive als auch negative Steigungen beschränkt. Es gibt also ein , sodass für alle mit die Ungleichung gilt: . Diese Zahl wird auch Lipschitz-Konstante genannt. Umstellen der Gleichung durch Multiplikation mit liefert:
Diese Ungleichung wird für die Definition der Lipschitz-Stetigkeit herangezogen. Wenn ein diese Ungleichung für alle erfüllt, so ist die Änderung der Funktion betragsmäßig beschränkt. Der Vorteil der Ungleichung ist, dass sie auch für erfüllt ist. So kann in der Definition die Bedingung wegfallen, welche für die Steigung benötigt wird.
Definition
BearbeitenDefinition (Lipschitz-Stetigkeit)
Sei eine Teilmenge von und sei eine Funktion. Dann heißt genau dann Lipschitz-stetig auf , wenn ein existiert, so dass für alle gilt.
Diese Definition kann auch in Quantorenschreibweise ausgedrückt werden:
Die rechte Seite der obigen Äquivalenz kann dabei folgendermaßen übersetzt werden:
Was bringt Lipschitz-Stetigkeit?
BearbeitenDie Lipschitz-Konstante einer Lipschitz-stetigen Funktion gibt uns eine obere Schranke für das Änderungsverhalten der Funktion. Das ist hilfreich bei der Abschätzung von Funktionswerten.
Nehmen wir an, wir haben einen Punkt aus dem Definitionsbereich und den dazugehörigen Funktionswert gegeben. Wir wollen mithilfe dieser Information nun zu einem anderen Punkt die Lage des dazugehörigen Funktionswerts eingrenzen. Das erreichen wir, indem wir aus der durch die Lipschitzkonstante gegebenen maximalen Änderung zwischen zwei Funktionswerten nach oben und nach unten abschätzen. Wegen der Lipschitzstetigkeit gilt
Daraus folgt durch Addition von die Abschätzung:
So haben wir eine Abschätzung, wo sich der Wert befindet.
Visualisierung
BearbeitenVisualisierung über Kegel
BearbeitenVisualisieren wir die Lipschitz-Bedingung: Wir zeichnen für eine Lipschitz-stetige Funktion durch den Funktionswert die Geraden und , die durch diesen Punkt verlaufen und die Steigung bzw. haben. Oben haben wir gesehen, dass die Lipschitz-Bedingung bedeutet, dass die Steigung aller beliebigen Sekanten durch den Punkt beschränkt ist. Das heißt, dass der Graph der Funktion zwischen diesen zwei Geraden verlaufen muss:

Diese Beschränkung der Funktion gilt für jedes beliebige im Definitionsbereich. In unserem Bild können wir die zwei Geraden den Graphen entlang „verschieben“ und der Graph von liegt immer im Bereich zwischen den zwei Geraden:
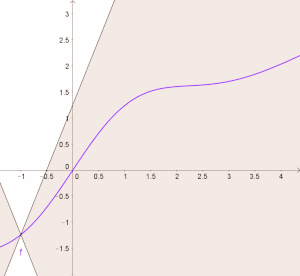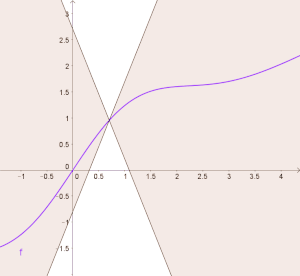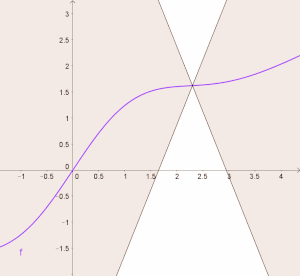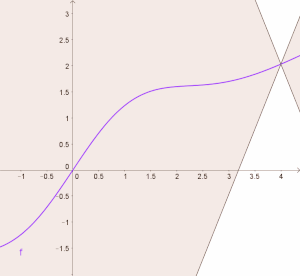
Falls die Funktion differenzierbar ist, so entspricht die Ableitung der Funktion in einem Punkt der Steigung der Tangenten in diesem Punkt. Aus dieser Visualisierung sieht man, dass die Ableitung einer Lipschitz-stetigen Funktion nicht größer werden kann als , bzw. nicht kleiner als , und somit der Betrag der Ableitung dieser Funktion beschränkt ist.
Unterschied zur gleichmäßigen Stetigkeit
Bearbeiten
Ebenso wie die Lipschitz-Stetigkeit ist auch die gleichmäßige Stetigkeit eine globale Eigenschaft. Anders als die Lipschitz-Stetigkeit macht die gleichmäßige Stetigkeit aber keine Aussage über das Änderungsverhalten einer Funktion. Das ist ein Nachteil, wenn etwa die Lage eines Funktionswertes anhand eines Funktionswertes abgeschätzt werden soll.
Bei der Lipschitz-Stetigkeit herrscht ein linearer Zusammenhang zwischen dem Abstand und der größtmöglichen Differenz . Das ist bei der gleichmäßigen Stetigkeit nicht der Fall, denn die Beschränkung der Funktionswerte ist für alle mit dieselbe. Somit liefern die mit zunehmender Nähe zu schmaler werdenden Kegel eine genauere Abschätzung als das „--Rechteck“ der gleichmäßigen Stetigkeit. Zwar kann man beliebig klein wählen, um die Lage von genauer einzugrenzen. Allerdings kann es sein, dass dann auch sehr klein werden muss, damit die Funktion das Rechteck nicht verlässt. Dies ist beispielsweise bei der Wurzelfunktion an der Stelle der Fall.
Zusammenhang mit gleichmäßiger Stetigkeit
BearbeitenWie hängt dieser neue Begriff der Lipschitz-Stetigkeit nun mit den vorherigen Begriffen der Stetigkeit und der gleichmäßigen Stetigkeit zusammen? Es stellt sich heraus, dass Lipschitz-Stetigkeit stärker ist als gleichmäßige Stetigkeit: Jede Lipschitz-stetige Funktion ist gleichmäßig stetig, aber nicht jede gleichmäßig stetige Funktion ist auch Lipschitz-stetig.
Lipschitz-stetige Funktionen sind gleichmäßig stetig
BearbeitenSatz (Lipschitz-Stetigkeit impliziert gleichmäßige Stetigkeit)
Sei und eine auf Lipschitz-stetige Funktion. Dann ist auch gleichmäßig stetig auf ihrem Definitionsbereich.
Beweis (Lipschitz-Stetigkeit impliziert gleichmäßige Stetigkeit)
Erinnern wir uns an die Definition der gleichmäßigen Stetigkeit: Eine Funktion heißt gleichmäßig stetig, falls für alle ein existiert, so dass für alle mit gilt, dass ist.
Sei also beliebig vorgegeben. Wir müssen nun ein finden, so dass für alle Werte mit der Abstand der Funktionswerte erfüllt. Nach Voraussetzung ist Lipschitz-stetig. Also existiert ein , so dass für alle .
Welchen Abstand dürfen die Werte haben, damit erfüllt ist? Hierzu reicht es, den Abstand kleiner als zu wählen. Wir setzen also . Hier ist jedoch etwas Vorsicht angebracht, denn die Lipschitz-Konstante könnte Null sein. Deswegen nutzen wir eine Fallunterscheidung:
Fall 1:
Falls , dann folgt aus der Lipschitz-Bedingung, dass für alle erfüllt ist. Damit ist aber beziehungsweise für alle . Somit ist die Funktion konstant, und damit auch gleichmäßig stetig. Für ein beliebig vorgegebenes kann jedes gewählt werden.
Fall 2:
Falls , so wähle . Seien nun mit . Dann folgt aus der Lipschitz-Stetigkeit:
In beiden Fällen erhalten wir die gleichmäßige Stetigkeit und der Satz ist bewiesen.
Nicht alle gleichmäßig stetigen Funktionen sind Lipschitz-stetig
BearbeitenNun möchten wir uns noch überlegen, dass nicht alle gleichmäßig stetigen Funktionen Lipschitz-stetig sind. Dafür genügt es, ein Gegenbeispiel anzugeben, also eine Funktion, die zwar gleichmäßig stetig, aber nicht Lipschitz-stetig ist. Ein solches Gegenbeispiel liefert die Wurzelfunktion auf . Für diese ist bewiesen, dass sie gleichmäßig stetig ist. Jetzt zeigen wir noch, dass sie nicht Lipschitz-stetig ist. Betrachte also:
Angenommen, sie wäre Lipschitz-stetig. Dann würde ein existieren, so dass für alle gilt: . Damit würde dann für alle mit oder folgen:
Wählt man aber zum Beispiel und , so ist:
Das liefert einen Widerspruch und somit ist nicht Lipschitz-stetig auf .
Lipschitz-Stetigkeit impliziert Stetigkeit
BearbeitenLipschitz-Stetigkeit impliziert Stetigkeit, was sich direkt aus dem vorherigen Abschnitt ergibt: Da Lipschitz-stetige Funktionen gleichmäßig stetig sind, sind sie insbesondere stetig. Das ist auch anschaulich klar, wenn wir uns überlegen, warum eine unstetige Funktion nicht Lipschitz-stetig sein kann:
Erinnern wir uns an die erste grobe Intuition zur Stetigkeit. Nach ihr sind stetige Funktionen solche Funktionen, die keine „Sprungstellen“ aufweisen:

Die abgebildete Funktion ist offensichtlich unstetig in . Stellen wir uns nun vor, wir legen eine Gerade durch den Punkt beim -Wert der Sprungstelle des Graphen, und durch einen weiteren Punkt des Graphen bei . Diese Gerade ist dann eine Sekante des Graphen.

Lässt man nun den Schnittpunkt bei von rechts immer näher an die Sprungstelle bei wandern, dann wird diese Sekante immer steiler und die Steigung geht gegen unendlich. Insbesondere ist es unmöglich, ein zu finden, das die Steigung der Sekanten beschränkt: Haben wir ein solches gewählt, rücken wir einfach von rechts noch ein Stückchen näher an die Sprungstelle heran und finden so früher oder später ein neues , für welches die Sekantensteigung größer als ist.
Damit sind (intuitiv betrachtet) alle Funktionen mit Sprungstellen nicht Lipschitz-stetig. Wenn wir dies nach dem Prinzip der Kontraposition umkehren, so sind alle Lipschitz-stetigen Funktionen stetig. Funktionen, deren Steigung begrenzt ist und die damit Lipschitz-stetig sind, können keine Sprungstellen aufweisen:

Beispiele
BearbeitenBeispiel (Lipschitz-Stetigkeit der Identitätsfunktion)
Die Identität mit ist Lipschitz-stetig auf ganz mit Lipschitzkonstante , denn es gilt für alle :
Beispiel (Lipschitz-Stetigkeit der eingeschränkten Quadratfunktion)
Betrachte die auf dem abgeschlossenen Intervall definierte Funktion
Dabei ist beliebig mit . Diese ist ebenfalls Lipschitz-stetig, denn es gilt für alle :
Somit kann als Lipschitzkonstante gewählt werden.
Beispiel (Lipschitz-Unstetigkeit der Quadratfunktion)
Betrachten wir die auf den ganzen reellen Zahlen definierte Quadratfunktion mit . Diese ist nicht mehr Lipschitz-stetig. Angenommen, es gäbe eine Zahl mit für alle . Zunächst ist:
Wegen müsste für beliebige gelten. Eine Lipschitz-Konstante mit dieser Eigenschaft kann es nicht geben. So ist (nachdem man ein gewählt hat) für und diese Ungleichung nicht erfüllt. Dieser Widerspruch zeigt, dass die Quadratfunktion auf ganz nicht Lipschitz-stetig ist.
Aufgaben
BearbeitenLineare Funktionen sind Lipschitz-stetig
BearbeitenAufgabe (Lineare Funktionen sind Lipschitz-stetig)
Zeige, dass jede lineare Funktion mit Lipschitz-stetig ist.
Lösung (Lineare Funktionen sind Lipschitz-stetig)
Seien beliebig. Dann gilt:
ist also Lipschitz-stetig mit der Lipschitz-Konstanten .
Quadratische Funktionen und Lipschitz-Stetigkeit
BearbeitenAufgabe (Quadratische Funktionen und Lipschitz-Stetigkeit)
Zeige, dass jede quadratische Funktion mit für und auf dem abgeschlossenen Intervall Lipschitz-stetig ist und auf ganz nicht Lipschitz-stetig ist.
Lösung (Quadratische Funktionen und Lipschitz-Stetigkeit)
Mit einer binomischen Formel bekommen wir:
Sei nun zuerst . Dort gilt dann mit der Dreiecksungleichung:
Eine geeignete Lipschitz-Konstante ist damit gegeben durch .
Dann sehen wir uns noch den Fall des Definitionsbereichs an. Angenommen, wäre Lipschitz-stetig. Dann würde ein mit für alle existieren. Mit der obigen Rechnung folgt dann:
Also müsste für alle gelten. Wählt man beispielsweise und , dann erhält man:
Das liefert uns einen Widerspruch zu der Aussage oben, also ist auf nicht Lipschitz-stetig.
Lipschitz-Stetigkeit und die Hyperbelfunktion
BearbeitenAufgabe
Es sei mit .
- Zeige, dass Lipschitz-stetig ist, und bestimme eine Lipschitzkonstante für diese Funktion.
- Untersuche, ob auch Lipschitzstetig ist.
Lösung
Lösung Teilaufgabe 1:
Seien . Dann gilt:
ist daher auf Lipschitz-stetig mit Lipschitz-Konstante .
Lösung Teilaufgabe 2:
Angenommen ist Lipschitzstetig, dann gibt es ein mit für alle . Für ist dies äquivalent zu . Nun unterscheiden wir die Fälle und :
Fall 1:
Für und ist . ↯
Fall 2:
Für und erhalten wir den Widerspruch:
Praktisches Kriterium für Lipschitz-Stetigkeit: Der Schrankensatz
BearbeitenWir werden später mit Hilfe des Mittelwertsatzes ein praktisches Kriterium für die Lipschitz-Stetigkeit einer differenzierbaren Funktion herleiten, den Schrankensatz. Dieser lautet:
Satz (Schrankensatz (Lipschitz-Variante))
Sei stetig und in differenzierbar. Weiter sei die Ableitungsfunktion beschränkt. Dann ist Lipschitz-stetig mit Lipschitz-Konstante . Insbesondere ist jedes auf stetig-differenzierbare Lipschitz-stetig.















![{\displaystyle {\begin{aligned}&&\left|{\frac {f(x)-f({\tilde {x}})}{x-{\tilde {x}}}}\right|&\leq L\\[0.3em]&\iff &\left|f(x)-f({\tilde {x}})\right|&\leq L|x-{\tilde {x}}|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a832717e6411cdeb9a88e8e25caa24bb60dbbeb)









![{\displaystyle {\begin{array}{cc}&f:D\rightarrow \mathbb {R} {\text{ ist Lipschitz-stetig }}\\[1em]\iff &\exists L\geq 0\,\forall x,{\tilde {x}}\in D:|f(x)-f({\tilde {x}})|\leq L\cdot |x-{\tilde {x}}|\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7c029ee6e85102dba7deab442f949cc40dc3763)

































![{\displaystyle {\begin{aligned}|f(x)-f(y)|&\leq L\cdot |x-y|<L\cdot \delta \\[0.5em]&=L\cdot {\frac {\epsilon }{L}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/941384ad0bb3a0ec890bda94770a2579e440e133)






![{\displaystyle {\begin{aligned}&&|{\sqrt {x}}-{\sqrt {y}}|&<L\cdot |x-y|\\[0.3em]&\implies &{\frac {|{\sqrt {x}}-{\sqrt {y}}|\cdot |{\sqrt {x}}+{\sqrt {y}}|}{|{\sqrt {x}}+{\sqrt {y}}|}}&<L\cdot |x-y|\\[0.3em]&\implies &{\frac {1}{|{\sqrt {x}}+{\sqrt {y}}|}}\cdot |x-y|&<L\cdot |x-y|\\[0.3em]&\implies &{\frac {1}{|{\sqrt {x}}+{\sqrt {y}}|}}&<L\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29da71a9bccf6e3a8a79681e23db686978a6b577)


![{\displaystyle {\begin{aligned}{\frac {1}{|{\sqrt {x}}+{\sqrt {y}}|}}&={\frac {1}{{\frac {1}{\sqrt {4L^{2}}}}+0}}\\[0.5em]&={\frac {1}{\frac {1}{2L}}}=2L>L\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7139e39e14b1b47d76d3c597d7ac6601136c13e9)







![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle {\begin{aligned}f:[a,b]&\to \mathbb {R} \\x&\mapsto x^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea31b7b7e80ae4e3c53f3c5bdd3ecca38780b815)


![{\displaystyle x,y\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e14f38807bc231b9e43d45c8e909d463afb17b5)
![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|x^{2}-y^{2}|\\[0.3em]&=|(x+y)\cdot (x-y)|\\[0.3em]&=|x+y|\cdot |x-y|\\[0.3em]&\leq \left(\left|x\right|+\left|y\right|\right)\cdot \left|x-y\right|\\[0.3em]&\leq 2\cdot \max\{\left|x\right|,\left|y\right|\}\cdot \left|x-y\right|\\[0.3em]&\leq 2\cdot \max\{|a|,|b|\}\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c7596d1375f555a2ae852ee7568c884dfd28aff)







![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|a\cdot x+b-(a\cdot y+b)|\\[0.3em]&=|a\cdot (x-y)|=|a|\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/399e0f80c0c8ca39510581c9f5728cd77a0423ca)




![{\displaystyle [-2,2]\subseteq \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae62cde2c2776c5c544d576b2f2499c3e67f0c1)
![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|ax^{2}+bx+c-(ay^{2}+by+c)|\\[0.3em]&=|a(x^{2}-y^{2})+b(x-y)|\\[0.3em]&=|a(x+y)(x-y)+b(x-y)|\\[0.3em]&=|a(x+y)+b|\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f27f899cfaa85609769b8686e77ed5c081381eb)
![{\displaystyle x,y\in [-2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dcf93923fba30c5021c0156a8ad5c66c5e40e68)
![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|a(x+y)+b|\cdot |x-y|\\[0.3em]&\leq (|a(x+y)|+|b|)\cdot |x-y|\\[0.3em]&\leq (|a|\cdot |x+y|+|b|)\cdot |x-y|\\[0.3em]&\leq (|a|\cdot (|x|+|y|)+|b|)\cdot |x-y|\\[0.3em]&\leq (4|a|+|b|)\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1c07bd5c4bfadecd79404fe6e8c5e84ce6af1b)


![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|a(x+y)+b|\cdot |x-y|\\[0.3em]&\leq L\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63193e8a8d2fb7768ae5c981946f728026f84627)


![{\displaystyle {\begin{aligned}|a(x+y)+b|&=\left|a\left({\frac {L-b+1}{a}}+0\right)+b\right|\\[0.3em]&=|L+1|>L\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abdafdd771ff0ace1755cd67cdd045db779082f2)



![{\displaystyle f|_{(0,1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/221a5e5788ff3672911cf7eabc32f3e9b323ab43)

![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=\left|{\frac {1}{x}}-{\frac {1}{y}}\right|=\left|{\frac {y-x}{xy}}\right|\\[0.3em]&={\frac {1}{xy}}\cdot |x-y|\\[0.3em]&{\color {OliveGreen}\left\downarrow \ x,y\geq 1\right.}\\[0.3em]&\leq 1\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52a16ccccbe937089e72808ccc36a99070f62c12)


![{\displaystyle x,y\in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53ed60a602ababea356ccb07866f0c33ae8180b1)




![{\textstyle x={\frac {1}{2L}}\in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ba32fe53ed1369d83b64159f7ad4a033b728200)


![{\displaystyle x=2L\in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a47a2c70fb14c7ff8b23b8ebb2e73d877b2294fb)

![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)


