Komplexe Konjugation und Betrag komplexer Zahlen – Serlo „Mathe für Nicht-Freaks“
Betrag einer komplexen Zahl
BearbeitenMotivation des Betrags
BearbeitenIm Umgang mit den reellen Zahlen haben wir die Betragsfunktion kennengelernt, mit der wir den absoluten Abstand zur Zahl Null angeben konnten. An der reellen Zahlengerade visualisiert sieht das wie folgt aus:
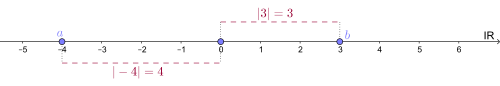
Auch in der komplexen Ebene können wir den Abstand einer komplexen Zahl zum Nullpunkt bestimmen. Hierzu verwenden wir den Satz des Pythagoras. Sei eine komplexe Zahl:
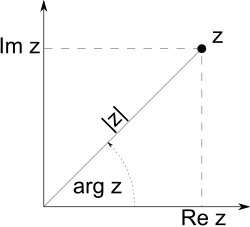
Mit dem Satz des Pythagoras gilt für den Abstand vom Nullpunkt die Gleichung . Durch Wurzelziehen auf beiden Seiten, kann bestimmt werden. Es ist nämlich:
Mit dem Betrag können einige Konzepte der reellen Zahlen auf die komplexen Zahlen übertragen werden. So wie in den reellen Zahlen der Abstand zwischen und ist, so ist auch in den komplexen Zahlen der Abstand zwischen und . Mit dem Abstand wiederum können Begriffe wie der Grenzwert definiert werden: Eine komplexe Zahl ist genau dann der Grenzwert einer Folge von komplexen Zahlen, wenn der Abstand zwischen dem Grenzwert und den Folgengliedern beliebig klein wird.
Definition des komplexen Betrags
BearbeitenDefinition (Betrag einer komplexen Zahl)
Es sei . Dann setzen wir und nennen die Zahl den Betrag von .
Hinweis
Der oben definierte Betrag auf den komplexen Zahlen stimmt für die reellen Zahlen mit dem üblichen Betrag überein. Sei . Dann gilt:
Komplexe Konjugation
BearbeitenMotivation der Konjugation
BearbeitenDie imaginäre Einheit erfüllt als eine Wurzel von die Gleichung . Wir können uns die Multiplikation als eine -Drehung um den Nullpunkt vorstellen. Nun ist die Multiplikation wegen der Gleichung dasselbe wie . Damit ist eine Operation, die bei zweifacher Anwendung einer -Drehung entspricht.
Es ist naheliegend, dass die Multiplikation mit einer -Drehung entspricht. Damit ist die imaginäre Einheit wegen gleich derjenigen Zahl, die aus einer Drehung um der Zahl entsteht:
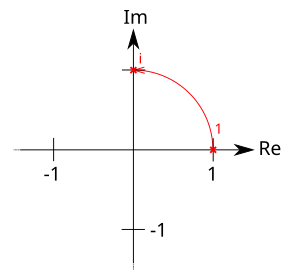
Allgemein gängig ist es, gegen den Uhrzeigersinn zu drehen. So liegt dort, wo im die auf der -Achse liegt. Jedoch hätte man genau so gut im Uhrzeigersinn drehen können. Dann läge das an der Stelle der auf der -Achse:

Auch über diese alternative Drehung hätten wir die komplexen Zahlen herleiten können. So hätten wir eine andere Menge von komplexen Zahlen erhalten, bei der die imaginäre Einheit unterhalb der -Achse liegt. Bei dieser alternativen Menge von komplexe Zahlen sind die Rollen von und vertauscht. Wenn wir also überall vertauschen, sollten wesentliche Eigenschaften und Strukturen, die durch die Zahlenbereichserweiterung gewonnen wurden, erhalten bleiben. Eine solche Vertauschung entspricht der Abbildung:
Bei dieser Abbildung wird der Imaginärteil mit multipliziert. Dies entspricht einer Spiegelung der komplexen Zahl an der reellen Achse, also der -Achse:
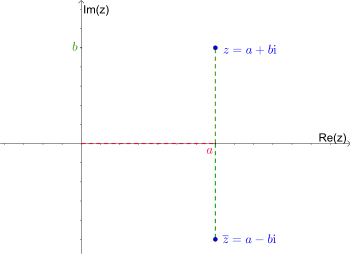
Ein Beispiel hierfür sind die Nullstellen der Funktion . Es ist . Daher ist eine Nullstelle von . Andererseits gilt auch und damit ist eine weitere Nullstelle. Betrachten wir mit der Nullstelle . Man könnte meinen, dass das Negative der Zahl, also , eine weitere Nullstelle ist. Dies ist leider nicht der Fall. Wenn wir allerdings mit austauschen, also die komplexe Zahl betrachten, erhalten wir eine weitere Nullstelle:
Für die Nullstelle eines Polynoms scheint das an der reellen Achse gespiegelte eine weitere Nullstelle zu sein. Dies ist im Übrigen für alle Polynome mit rein reellen Koeffizienten der Fall. Dies weist darauf hin, dass die Abbildung eine Besondere ist. Diese Abbildung wird komplexe Konjugation genannt.
Definition der komplexen Konjugation
BearbeitenDefinition (Komplexe Konjugation einer komplexen Zahl)
Es sei . Dann heißt die Abbildung komplexe Konjugation und die Zahl die zu komplex konjugierte Zahl.
Übersicht: Eigenschaften des Betrags und der komplexen Konjugation
BearbeitenEigenschaften der komplexen Konjugation
BearbeitenFür alle und gilt:
Eigenschaften des Betrags einer komplexen Zahl
BearbeitenFür alle und gilt:
- und (positive Definitheit)
- (Multiplikativität)
- und
- (Dreiecksungleichung)
Rechenregeln der komplexen Konjugation
BearbeitenKonjugation verändert reelle Zahlen nicht
BearbeitenSatz (Konjugation verändert reelle Zahlen nicht)
Für eine Zahl gilt genau dann, wenn rein reell ist, d.h. .
Beweis (Konjugation verändert reelle Zahlen nicht)
Beweisschritt:
Sei mit und . Es ist dann
Damit ist und somit eine reelle Zahl.
Beweisschritt:
Sei eine reelle Zahl. Also ist . Wir haben:
Involution
BearbeitenSatz (Involution)
Für eine komplexe Zahl gilt:
Beweis (Involution)
Sei mit . Dann gilt:
Die kann auch folgendermaßen erklärt werden: ist die Spiegelung von an der reellen Achse. Damit ist die Spiegelung von der Spiegelung und somit die ursprüngliche komplexe Zahl.
Verträglichkeit mit Addition
BearbeitenSatz (Verträglichkeit mit Addition)
Für komplexe Zahlen gilt:
Beweis (Verträglichkeit mit Addition)
Sei von der Form , wobei und von der Form , wobei . Dann gilt:
Verträglichkeit mit Multiplikation
BearbeitenSatz (Verträglichkeit mit Multiplikation)
Für komplexe Zahlen gilt:
Beweis (Verträglichkeit mit Multiplikation)
Sei von der Form , wobei und von der Form , wobei . Dann gilt:
Verträglichkeit der Konjugation bei endlichen Summen und Produkten
BearbeitenWir wissen, wie sich die Konjugation bei der Summe und dem Produkt zweier Zahlen verhält. Was passiert bei Summen und Produkten mit drei oder mehr Zahlen wie bei ? Wir behelfen uns mit einem Trick: Wir betrachten zuerst als eine einzige komplexe Zahl und benutzen zwei Mal den Satz zum Zusammenhang zwischen Konjugation und Summe:
Es ist auch für drei Summanden egal, ob wir zuerst alles summieren und dann auf die entstandene Zahl die Konjugation anwenden, oder ob wir zuerst jede Zahl konjugieren und dann alles summieren. Dies geht allgemein für beliebig lange Summen und Produkte von komplexen Zahlen, wie wir es im Folgenden formal beweisen werden. Hierzu führen wir einen Induktionsbeweis über die Anzahl der Summanden bzw. Faktoren. Auch verwenden wir die kompakte Schreibweise für endliche Summen und Produkte.
Satz (Verträglichkeit für beliebig viele komplexe Zahlen)
Für jedes und alle komplexe Zahlen gilt:
Beweis (Verträglichkeit für beliebig viele komplexe Zahlen)
Wir beweisen diesen Satz für die Summe über vollständige Induktion. Der Beweis für das endliche Produkt kann analog geführt werden:
Aussageform, deren Allgemeingültigkeit für bewiesen werden soll:
1. Induktionsanfang:
2. Induktionsschritt:
2a. Induktionsvoraussetzung:
2b. Induktionsbehauptung:
2c. Beweis des Induktionsschritts:
Berechnung des Real- und Imaginärteils
BearbeitenSatz (Real- und Imaginärteils)
Für eine komplexe Zahl gilt:
Beweis (Real- und Imaginärteils)
Sei mit . Wir rechnen die Gleichung von der rechten Seite ausgehend nach:
Berechnung des Betrags über die Konjugation
BearbeitenSatz (Berechnung des Betrags über die Konjugation)
Für alle komplexen Zahlen ist . Damit ist .
Beweis (Berechnung des Betrags über die Konjugation)
Sei eine beliebige komplexe Zahl mit . Wir berechnen . Es ist und . Also gilt
Da reell ist und die Basis nicht negativ ist, können wir die Wurzel ziehen und erhalten die reelle Zahl .
Berechnung des Reziproken mit der Konjugation
BearbeitenSatz (Berechnung des Reziproken mit der Konjugation)
Für alle komplexe Zahlen ist .
Beweis (Berechnung des Reziproken mit der Konjugation)
Sei eine beliebige komplexe Zahl. Wir wollen zeigen. Dafür beweisen wir . Mit folgt
Weil die Inverse in einem Körper eindeutig ist, folgt . Dies beweist, dass gleich dem Reziproken von ist.
Hinweis
Beim Beweis die komplexen Zahlen bilden einen Körper haben wir auch eine multiplikative Inverse von hergeleitet. Dort haben wir gesehen . Das ist konsistent mit der neuen Darstellung durch komplexe Konjugation:
Konjugation bei Brüchen
BearbeitenSatz (Konjugation bei Brüchen)
Für alle komplexen Zahlen mit gilt:
Beweis (Konjugation bei Brüchen)
Wir wissen bereits, dass für das Reziproke einer komplexen Zahl gilt: . Außerdem haben wir gesehen, dass reelle Zahlen durch die Konjugation nicht verändert werden und dass die Konjugation mit der Multiplikation verträglich ist. Wir zeigen zunächst: . Hierfür benutzen wir, dass reell ist und dass gilt.
Daraus folgt für die Konjugation von Brüchen komplexer Zahlen mit :
Eigenschaften der komplexen Betragsfunktion
BearbeitenPositive Definitheit
BearbeitenSatz (Positive Definitheit)
Sei eine komplexe Zahl, dann gilt:
Beweis (Positive Definitheit)
Sei in kartesischer Form gegeben. Dann gilt . Nun müssen wir noch die Äquivalenz beweisen. Dafür zeigen wir zwei Implikationen:
Beweisschritt:
Sei . Dann gilt . Somit folgt .
Beweisschritt:
Diese Richtung zeigen wir durch Kontraposition. Sei dafür . Daraus folgt oder . Wenn gilt . Wenn gilt . In jedem Fall folgt und damit .
Multiplikativität
BearbeitenSatz (Multiplikativität)
Für gilt .
Beweis (Multiplikativität)
Seien und . Dann folgt
Da die Basen und der beiden Quadrate auf beiden Seiten nicht negativ ist, können wir auf beiden Seiten die Wurzel ziehen. Wir erhalten dann .
Abschätzung Real- und Imaginärteil
BearbeitenSatz
Für alle gilt und .
Beweis
Sei mit . Dann folgt mit :
Genauso folgt mit :
Dreiecksungleichung
BearbeitenSatz (Dreiecksungleichung)
Für alle gilt .
Beweis (Dreiecksungleichung)
Seien und . Um den Betrag abzuschätzen nutzen wir die Beziehung :
Abschätzung des Betrags
BearbeitenSatz
Für alle gilt .
Beweis
Wir zeigen zuerst, dass die Ungleichung für beide Seiten im Quadrat gilt.
Die beiden Basen und sind nicht negative Zahlen sind, können wir die Wurzel auf beiden Seiten der Ungleichung ziehen. Diese Wurzel erhält Ungleichungen und damit ist .
Umgekehrte Dreiecksungleichung
BearbeitenSatz (Umgekehrte Dreiecksungleichung)
Für komplexe Zahlen gilt .
Beweis (Umgekehrte Dreiecksungleichung)
Um eine Ungleichung zu zeigen, können wir alternativ die beiden Ungleichungen und beweisen. Um diese Technik in diesem Beweis anzuwenden, müssen wir die beiden Ungleichungen und beweisen.
Beginnen wir mit der ersten Ungleichung. Wir verwenden die Dreiecksungleichung des komplexen Betrag und den Trick des „Einschiebens einer “:
Durch Umformung erhalten wir . Die zweite Ungleichung zeigen wir analog, wobei die Rollen von und vertauscht sind. Zusätzlich formen wir schrittweise in um:
Es folgt . Damit haben wir die beiden Ungleichungen und bewiesen. Daraus folgt die Ungleichung .

















![{\displaystyle {\begin{aligned}|z|&={\sqrt {{\text{Re}}(z)^{2}+{\text{Im}}(z)^{2}}}={\sqrt {a^{2}+0^{2}}}={\sqrt {a^{2}}}\\[0.3em]&={\begin{cases}a,&{\text{falls }}a\geq 0,\\-a,&{\text{falls }}a<0.\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0776cd9736eac17a1323184aa44bd75f831cfe33)












































































![{\displaystyle {\begin{aligned}{\overline {\sum _{k=1}^{n+1}z_{k}}}&={\overline {\sum _{k=1}^{n}z_{k}+z_{n+1}}}={\color {OliveGreen}{\overline {\sum _{k=1}^{n}z_{k}}}}+{\overline {z_{n+1}}}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{Induktionsvoraussetzung}}\right.}\\[0.5em]&={\color {OliveGreen}\sum _{k=1}^{n}{\overline {z_{k}}}}+{\overline {z_{n+1}}}=\sum _{k=1}^{n+1}{\overline {z_{k}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53ca91ac23009d826c9f22840db036036077bc0)
![{\displaystyle {\begin{aligned}{\frac {1}{2}}\cdot \left(w+{\overline {w}}\right)&={\frac {1}{2}}\cdot (a+b\,\mathrm {i} +(a-b\,\mathrm {i} ))\\[0.3em]&={\frac {1}{2}}\cdot (a+a+b\,\mathrm {i} -b\,\mathrm {i} )\\[0.3em]&={\frac {1}{2}}\cdot (2a)=a=\mathrm {Re} (w)\\[0.3em]{\frac {1}{2\mathrm {i} }}\cdot \left(w-{\overline {w}}\right)&={\frac {1}{2\mathrm {i} }}\cdot (a+b\,\mathrm {i} -(a-b\,\mathrm {i} ))\\[0.3em]&={\frac {1}{2\mathrm {i} }}\cdot (a-a+b\,\mathrm {i} +b\,\mathrm {i} )\\[0.3em]&={\frac {1}{2\mathrm {i} }}\cdot (2b\,\mathrm {i} )=b=\mathrm {Im} (w)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b6dd35ba342d6e043ecae495bc28b4e3c14ccb5)


















![{\displaystyle {\begin{aligned}{\overline {\left({\frac {1}{w}}\right)}}&={\overline {\left({\frac {\overline {w}}{|w|^{2}}}\right)}}={\overline {\left({\overline {w}}\cdot {\frac {1}{|w|^{2}}}\right)}}={\overline {\left({\overline {w}}\right)}}\cdot {\overline {\left({\frac {1}{|w|^{2}}}\right)}}\\[0.5em]&={\overline {\left({\overline {w}}\right)}}\cdot {\frac {1}{|w|^{2}}}={\overline {\left({\overline {w}}\right)}}\cdot {\frac {1}{|{\overline {w}}|^{2}}}={\frac {\overline {\left({\overline {w}}\right)}}{|{\overline {w}}|^{2}}}={\frac {1}{\overline {w}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23a8884c0a9bb19894d4ed631ab071b120b97aa0)


























![{\displaystyle {\begin{aligned}|w+z|^{2}&=(w+z){\overline {(w+z)}}\\&=(w+z)({\overline {w}}+{\overline {z}})\\&=w{\overline {w}}+w{\overline {z}}+{\overline {w}}z+{\overline {z}}z\\&=|w|^{2}+(w{\overline {z}}+{\overline {w{\overline {z}}}})+|z|^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Für }}v\in \mathbb {C} {\text{ gilt }}v+{\overline {v}}=2\mathrm {Re} (v)\right.}\\[0.3em]&=|w|^{2}+2\mathrm {Re} (w{\overline {z}})+|z|^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \mathrm {Re} (w{\overline {z}})\leq |\mathrm {Re} (w{\overline {z}})|\leq |w{\overline {z}}|=|w||{\overline {z}}|=|w||z|\right.}\\[0.3em]&\leq |w|^{2}+2|w||z|+|z|^{2}\\&=(|w|+|z|)^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21aa007456506df58f207b132963c8a448074877)













