Grundlagen der Mathematik: Zusammenfassung – Serlo „Mathe für Nicht-Freaks“
Logik
BearbeitenMind Map
Wahrheitstabellen der Junktoren
BearbeitenTautologien
Bearbeiten| Name der Umformungsregeln | Tautologie | Bedeutung |
|---|---|---|
| Assoziativgesetze | Bei der Disjunktion und bei der Konjunktion ist es egal, in welcher Weise die einzelnen Teilaussagen verknüpft werden. | |
| Kommutativgesetze | Bei der Disjunktion und bei der Konjunktion ist es egal, in welcher Reihenfolge die einzelnen Teilaussagen verknüpft werden. | |
| Distributivgesetze | Eine Disjunktion kann in eine Konjunktion reingezogen werden und umgekehrt. | |
| Absorptionsgesetze | ||
| Idempotenzgesetze | ||
| Gesetze vom ausgeschlossenen Dritten | ||
| Darstellung von Implikation und Äquivalenz | Mit Hilfe dieser Gesetze kann die Implikation und die Äquivalenz auf Aussagen mit anderen Junktoren zurückgeführt werden. So können bestimmte Aufgaben gelöst werden (wie: Finden sie die Negation der Implikation). | |
| Prinzip der Kontraposition (Diese Äquivalenz kann insbesondere für Beweise verwendet werden) | ||
| Negation von zusammengsetzten Aussagen | Bei der Negation einer Und- bzw. Oder-Verknüpfung wird die Negation in die Klammer gesetzt und das entsprechende Symbol der Verknüpfung umgedreht. | |
| Negation quantifizierter Aussagen | ||
| Gesetze mit „wahr“ und „falsch“ | ||
| Doppelte Verneinung | Doppelte Verneinung ist wieder die Ausgangsaussage. | |
| Äquivalenzen zu quantifizierte Aussagen | Aussagen mit dem Allquantor können durch den Existenzquantor ausgedrückt werden und umgekehrt. | |
| Allquantoren sind untereinander vertauschbar. | ||
| Existenzquantoren sind untereinander vertauschbar. | ||
| Allquantoren können aus Konjunktionen rausgezogen werden. | ||
| Existenzquantoren können aus Disjunktionen rausgezogen werden. | ||
| Implikation zu quantifizierten Aussagen | Implikationen sind im Allgemeinen nicht umkehrbar. | |
Vokabelliste
Bearbeiten| natürliche Sprache | formale Schreibweise |
|---|---|
| nicht | |
| und | |
| oder *) | |
| Wenn , dann | |
| dann, wenn | |
| Aus folgt | |
| impliziert | |
| ist hinreichend für | |
| ist notwendig für | |
| Genau dann , wenn | |
| Dann und nur dann , wenn | |
| ist gleichwertig mit | |
| ist äquivalent zu | |
| ist notwendig und hinreichend für | |
| Für alle ist | |
| Jedes erfüllt | |
| Es ist A(x) für alle | |
| Für alle aus ist | |
| Jedes der Menge erfüllt | |
| Es ist A(x) für alle | |
| Es gibt ein mit | |
| Es existiert ein , so dass gilt | |
| Für mindestens ein gilt | |
| Es gibt ein aus mit | |
| Für mindestens ein gilt | |
| Es gibt genau ein mit | |
| Es existiert genau ein , so dass gilt | |
| Für genau ein gilt | |
| Es gibt genau ein aus mit | |
| Für genau ein gilt |
*) Hier ist „oder“ als „und/oder“ zu verstehen
Umformungsregeln zur Negation
Bearbeiten| zu bestimmende Negation | umgeformte Aussage |
|---|---|
Beweis
BearbeitenDefinition (Beweis)
Ein Beweis ist eine fehlerfreie Herleitung eines mathematischen Satzes aus Axiomen und bereits bewiesenen Aussagen.
Beweisarten
BearbeitenDirekter Beweis
BearbeitenWiderspruchsbeweis
BearbeitenBeweismethoden
BearbeitenVollständige Fallunterscheidung
BearbeitenBeweis durch Kontraposition
BearbeitenAnstatt eine Implikation zu beweisen, kann man alternativ auch die Implikation beweisen.
Vollständige Induktion
BearbeitenSei eine Aussageform in der freien Variablen . Sei (oder ) eine wahre Aussage (Induktionsanfang) und die Implikation für alle erfüllt (Induktionsschritt), dann ist die Aussageform allgemeingültig in .
Mengenlehre
BearbeitenMind Map
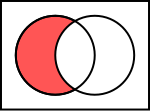
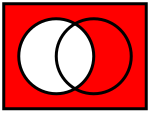
Verknüpfungen zwischen Mengen
BearbeitenGesetzmäßigkeiten
BearbeitenAssoziativgesetze
BearbeitenKommutativgesetze
BearbeitenDistributivgesetze
BearbeitenIdempotenzgesetze
BearbeitenAbsorptionsgesetze
BearbeitenDe-Morgansche Regeln
BearbeitenGesetzmäßigkeiten zur Differenz
BearbeitenWeitere Regeln
BearbeitenIm Folgenden sei die Grundmenge.
Relation
BearbeitenMind Map
Eigenschaften homogener, binärer Relationen
BearbeitenIm Folgenden sei eine homogene Relation auf der Grundmenge , also .
| Eigenschaft | Definition | Definition in formaler Schreibweise | Merkmale |
|---|---|---|---|
| reflexiv | Jedes Objekt der Grundmenge steht mit sich selbst in Relation. |
| |
| irreflexiv | Es gibt kein Objekt, welches mit sich selbst in Relation steht |
| |
| symmetrisch | Steht ein Objekt in Relation mit dem Objekt , dann steht auch in Relation mit |
| |
| antisymmetrisch | Zwei verschiedene Objekte und stehen nicht gegenseitig in Relation zueinander. |
| |
| transitiv | Steht mit und mit in Relation, dann steht auch mit in Relation. | ||
| linear | Für jeweils zwei Objekte und stehen mit und/oder mit in Relation. |
Abbildung
BearbeitenMind Map
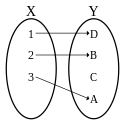
Eigenschaften von Abbildungen
BearbeitenDie folgende Tabelle bezieht sich auf Abbildungen .
| Eigenschaft | Definition | Definition in formaler Schreibweise | Beispiel |
|---|---|---|---|
| injektiv |
|
|
|
| surjektiv |
|
|
|
| bijektiv bzw. umkehrbar |
|
Eigenschaften binärer Verknüpfungen
BearbeitenDie folgende Tabelle bezieht sich auf binäre Verknüpfungen auf der Grundmenge .
| Eigenschaft | Definition | Definition in formaler Schreibweise |
|---|---|---|
| assoziativ | Werden mehrere Verknüpfungen hintereinander ausgeführt, ist die Reihenfolge, in welcher die einzelnen Verknüpfungen ausgerechnet werden, für das Ergebnis egal | |
| kommutativ | Für das Ergebnis ist die Reihenfolge der Operanden egal |
Mächtigkeit von Mengen
BearbeitenMind Map
Summe und Produkt
BearbeitenMind Map
Eigenschaften der Summen- und Produktschreibweise
Bearbeiten| Eigenschaft | Erklärung |
|---|---|
| Indexumbennungsregel: Die Indizes können beliebig umbenannt werden, solange die neu eingeführte Laufvariable nicht in Konflikt mit einer bereits definierten Variable tritt. | |
| Summen können in zwei Summen aufgeteilt werden. | |
| Spezialfall der obigen Eigenschaften bzw. Rekursionsschritt bei der rekursiven Definition der Summe. | |
| Konstantenregel: Konstanten können aus Summen rausgezogen werden. | |
| Allgemeines Kommutativgesetz: Die Reihenfolge der Summen bei Doppel- und damit auch bei Mehrfachsummen ist egal. | |
| Allgemeines Distributivgesetz |
| Eigenschaft | Erklärung |
|---|---|
| Indexumbennungsregel: Die Indizes können beliebig umbenannt werden, solange die neu eingeführte Laufvariable nicht in Konflikt mit einer bereits definierten Variable tritt. | |
| Produkte können in mehrere Produkte aufgeteilt werden. | |
| Spezialfall der obigen Eigenschaften bzw. Rekursionsschritt bei der rekursiven Definition des Produkts. | |
| Konstantenregel: Konstanten können aus Produkten rausgezogen werden (Beachte den dabei entstehenden Exponenten ). | |
| Allgemeines Kommutativgesetz: Die Reihenfolge der Produkte bei Doppel- und damit auch bei Mehrfachprodukten ist egal. |
Binomialkoeffizient
BearbeitenMind Map
















































































![{\displaystyle {\begin{array}{c}{\text{Prämissen}}\\[2ex]{\begin{array}{c}{\text{Fall }}F_{1}:\\{\color {Orange}|}\\{\color {Orange}{\text{logische}}}\\{\color {Orange}{\text{Schlussfolgerungen}}}\\{\color {Orange}\downarrow }\\{\text{zu beweisende Aussage}}\end{array}}{\begin{array}{c}{\text{Fall }}F_{2}:\\{\color {Orange}|}\\{\color {Orange}{\text{logische}}}\\{\color {Orange}{\text{Schlussfolgerungen}}}\\{\color {Orange}\downarrow }\\{\text{zu beweisende Aussage}}\end{array}}\ldots {\begin{array}{c}{\text{Fall }}F_{n}:\\{\color {Orange}|}\\{\color {Orange}{\text{logische}}}\\{\color {Orange}{\text{Schlussfolgerungen}}}\\{\color {Orange}\downarrow }\\{\text{zu beweisende Aussage}}\end{array}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf02969cd919a5581f3c35f1b4bceb808db49ea7)