MathemaTriX ⋅ Aufgaben alle. 00

< Mathematrix: BY GYM

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT

${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$	DEINE FESTE BEGLEITERIN
	FÜR DIE SCHULMATHEMATIK

EINFACH UND
VERSTÄNDLICH

GRATIS!^*

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Hoch
zum
Anfang

Klasse 5

Grundrechenartenvorrang

$\ (-41)+99:(3\cdot 7-32)-(48:12+5)\cdot (-5)\$
$\ (+120):(2\cdot 7-36:9)-(35:5-3\cdot 2)\cdot (-4)$
$\ (7\cdot 3-56:2):(45:3-4\cdot 2)$

Antwort

$-5$
$16$
$-1$

$\$	$\$
	$\$
	$\$

Strich und Punkt Bruchrechnungen

$\ {\frac {11}{3}}:{\frac {8}{13}}\qquad \quad$
$\ {\frac {11}{3}}-{\frac {8}{13}}\$
$\ -{\frac {11}{13}}-{\frac {2}{13}}\qquad$
${\frac {11}{3}}\cdot {\frac {8}{13}}$

Antwort

$\textstyle \ {\frac {143}{24}}\qquad$
$\textstyle \ {\frac {119}{39}}\qquad$
$\textstyle \ -{\frac {13}{13}}(=-1)\qquad$
$\textstyle \ {\frac {88}{39}}\qquad$

$\$	$\$
	$\$
	$\$

Direkte Proportionalität

(auch Schlussrechnung oder Dreisatz)

In EU produzierte im Jahr (365 Tage) 2016 eine Person durchschnittlich 6,5 Tonnen CO₂.

Wie viel war die Produktion pro Woche (7 Tage)?
Wie viele Tage hätte sie gebraucht, um 0,13 Tonnen zu produzieren?

Antwort

$\ x\approx 0{,}125\ \ t\quad$
$\ x=7,3\ Tage$

$\$	$\$
	$\$
	$\$

Einheiten und physikalische Größen

Ordnen Sie die passenden Einheiten zu den entsprechenden physikalischen Größen richtig zu:
Fläche eines Staates		$\qquad$	$\$ m²
Dauer einer Flugreise			$\$ km²
Dauer einer Schulpause			$\$ h
Fläche eines Zimmers			min $\quad$
Abstand zwischen den Augen $\quad$	$\quad$		$\$ s
Dauer eines Atemzugs			cm $\$

Antwort

Ordnen Sie richtig zu:
Fläche eines Staates	km²	$\qquad$	$\$ m²
Dauer einer Flugreise	h		$\$ km²
Dauer eine Schulpause	min		$\$ h
Fläche eines Zimmers	m²		$\$ min
Abstand zwischen den Augen $\quad$	cm $\quad$		s $\$
Dauer eines Atemzugs	s		cm $\$

$\$	$\$
	$\$
	$\$

Einheiten ohne Hochzahl

Rechnen Sie um:

0,577 mm in m
577 km in dm
0,793 kg in mg
0,000783 s in min
0,0773 Tage in min

Antwort

$0{,}000577\ m\qquad$
$5770000\ km\qquad$
$793000\ mg\qquad$
$0{,}00001305\ min\qquad$
$111{,}312\ min$

$\$	$\$
	$\$
	$\$

Klasse 6

Grundrechenartenvorrang

$\ (-41)+99:(3\cdot 7-32)-(48:12+5)\cdot (-5)\$
$\ (+120):(2\cdot 7-36:9)-(35:5-3\cdot 2)\cdot (-4)$
$\ (7\cdot 3-56:2):(45:3-4\cdot 2)$

Antwort

$-5$
$16$
$-1$

Mathematrix: Werkzeuge/ Links

Strich und Punkt Bruchrechnungen

$\ {\frac {11}{3}}:{\frac {8}{13}}\qquad \quad$
$\ {\frac {11}{3}}-{\frac {8}{13}}\$
$\ -{\frac {11}{13}}-{\frac {2}{13}}\qquad$
${\frac {11}{3}}\cdot {\frac {8}{13}}$

Antwort

$\textstyle \ {\frac {143}{24}}\qquad$
$\textstyle \ {\frac {119}{39}}\qquad$
$\textstyle \ -{\frac {13}{13}}(=-1)\qquad$
$\textstyle \ {\frac {88}{39}}\qquad$

Mathematrix: Werkzeuge/ Links

Direkte Proportionalität

(auch Schlussrechnung oder Dreisatz)

In EU produzierte im Jahr (365 Tage) 2016 eine Person durchschnittlich 6,5 Tonnen CO₂.

Wie viel war die Produktion pro Woche (7 Tage)?
Wie viele Tage hätte sie gebraucht, um 0,13 Tonnen zu produzieren?

Antwort

$\ x\approx 0{,}125\ \ t\quad$
$\ x=7,3\ Tage$

Mathematrix: Werkzeuge/ Links

Grundaufgaben der Prozentrechnung

Von wie vielen h sind 0,17 h 6510%?
Wie viel % von 0,17 h sind 6510 h?
Wie viel ist 0,17% von 6510 h?

Antwort

$\ x\approx 0{,}0026\ {\text{h}}\quad$
$\ x\approx 3830000\%\quad \$
$x\approx 11{,}1\ {\text{h}}\quad$

$\$	$\$
	$\$
	$\$

Bruchkürzen

Kürzen Sie folgende Brüche!

$\ {\frac {21}{14}}=\qquad$
$\ {\frac {21}{12}}=\qquad$
$\ {\frac {12}{39}}=\qquad$
$\ {\frac {39}{52}}=\qquad$
$\ {\frac {33}{99}}=\qquad$

Antwort

$\ {\frac {3}{2}}\qquad$
$\ {\frac {7}{4}}\qquad$
$\ {\frac {4}{13}}\qquad$

$\ {\frac {3}{4}}\qquad$
$\ {\frac {1}{3}}\qquad$

$\$	$\$
	$\ \$
	$\$

Kürzen mit Primfaktorzerlegung

$\ {\frac {6552}{4410}}=\qquad$
$\ {\frac {2184}{5544}}=\qquad$
$\ {\frac {56056}{32760}}=\qquad$

Antwort

$\ {\frac {52}{35}}\qquad$
$\ {\frac {13}{33}}\qquad$
$\ {\frac {77}{45}}$

$\$	$\$
	$\$
	$\$

Gemischte Zahlen

Gemischte Zahl in unechten Bruch:

$5{\frac {2}{7}}\ \qquad \ 1{\frac {1}{6}}\ \qquad \ 9{\frac {8}{9}}\ \$
Unechten Bruch in gemischte Zahl
${\frac {447}{11}}\ \qquad \ {\frac {9}{7}}\ \qquad \ {\frac {35}{5}}\ \$
Subtraktion:
$5-{\frac {52}{7}}\ \qquad \ 1-{\frac {1}{6}}\ \qquad \ {\frac {143}{9}}-10\ \quad \ {\frac {16}{17}}-1\$

Antwort

$\ {\tfrac {37}{7}}\qquad$ $\ {\tfrac {7}{6}}\qquad$ $\ {\tfrac {89}{9}}$
$\ 40{\tfrac {7}{11}}\qquad$ $\ 1{\tfrac {2}{7}}\qquad$ $\ 7$
$\ -{\tfrac {17}{7}}\qquad$ $\ {\tfrac {5}{6}}\qquad$ $\ {\tfrac {53}{9}}\qquad$ $\ -{\tfrac {1}{17}}$

$\$	$\$
	$\$
	$\$

Umformen Grundwissen Gegenrechnungen

Berechnen Sie jeweils die unbekannte Variable!

$\ c+5347=2744\qquad$
$\ {\tfrac {k}{7}}=13\qquad$
$\ 6f=168\qquad$

$\ x-592=-5426\qquad$
$\ 58m=986\qquad$
$\ 51w=900\qquad$

Antwort

$c=-2603\qquad$
$k=91\qquad$
$f=28$

$x=-4834\qquad$
$\textstyle m={\tfrac {493}{29}}=17\qquad$
$w=17{\tfrac {11}{17}}\approx 17{,}65$

$\$	$\$
	$\$
	$\$

Textaufgaben zu den Bruchrechnungen

In einem Staat mit ca. 9,702 Millionen EinwohnerInnen
und 1,32 Milliarden € Vermögen haben

99 Menschen $\textstyle \ {\frac {4}{15}}\$ des Vermögens ("Multimillionäre"),
noch 2640 Menschen $\textstyle \ {\frac {10}{33}}\$ des Vermögens ("Millionäre"),
noch 3,528 Millionen Menschen $\textstyle \ {\frac {4}{11}}\$ des Vermögens (Mittelschicht),
und die restlichen Menschen den Rest des Vermögens ("der Rest").

Antwort

$\textstyle {\frac {1}{98000}}\ {\text{der Menschen}}\qquad \ 352\ {\text{Millionen €}}\qquad$
$\textstyle {\frac {1}{3675}}\ {\text{der Menschen}}\qquad \ 400\ {\text{Millionen €}}\qquad$
$\textstyle {\frac {4}{11}}\ {\text{der Menschen}}\qquad \ 480\ {\text{Millionen €}}\qquad$
$\textstyle {\text{fast}}\ {\frac {7}{11}}\ {\text{der Menschen}}\qquad \ 88\ {\text{Millionen €}}\qquad$

$\$	$\$
	$\$
	$\$

Indirekte Proportionalität

Nach heutigem Stand der Wissenschaft gibt es eine bestimmte Grenze am Energieverbrauch auf der Erde. Nehmen wir an, dass bei 7 Milliarden Menschen dies einen durchschnittlichen Energieverbrauch von 3 kWh pro Stunde ist. Wie viel wäre er bei 15 Milliarden Menschen?

Antwort

$1{,}4\ {\text{kWh}}\qquad$

$\$	$\$
	$\$
	$\$

Einheiten und physikalische Größen

Ordnen Sie die passenden Einheiten zu den entsprechenden physikalischen Größen richtig zu:
Fläche eines Staates		$\qquad$	$\$ m²
Dauer einer Flugreise			$\$ km²
Dauer einer Schulpause			$\$ h
Fläche eines Zimmers			min $\quad$
Abstand zwischen den Augen $\quad$	$\quad$		$\$ s
Dauer eines Atemzugs			cm $\$

Antwort

Ordnen Sie richtig zu:
Fläche eines Staates	km²	$\qquad$	$\$ m²
Dauer einer Flugreise	h		$\$ km²
Dauer eine Schulpause	min		$\$ h
Fläche eines Zimmers	m²		$\$ min
Abstand zwischen den Augen $\quad$	cm $\quad$		s $\$
Dauer eines Atemzugs	s		cm $\$

Mathematrix: Werkzeuge/ Links

Einheiten ohne Hochzahl

Rechnen Sie um:

0,577 mm in m
577 km in dm
0,793 kg in mg
0,000783 s in min
0,0773 Tage in min

Antwort

$0{,}000577\ m\qquad$
$5770000\ km\qquad$
$793000\ mg\qquad$
$0{,}00001305\ min\qquad$
$111{,}312\ min$

Mathematrix: Werkzeuge/ Links

Klasse 7

Multiplikation von zwei Potenzen mit der gleichen Basis

${3^{-5}}\cdot {3^{6}}$
${b^{-2t}}\cdot {b^{-5t}}$

Antwort

$\$	$\$
	$\$
	$\$

Ausmultiplizieren mit einer oder zwei Klammer

Lösen Sie die Klammer auf und fassen Sie die daraus entstandenen Termen ggf. zusammen!

$\ 4v^{7}(7v^{4}+3v^{5}-2v)\ \quad$
$(2g^{5}-3g^{3})(5g^{2}+4g)$

Antwort

$\ 28v^{11}+12v^{12}-8v^{8}$
$\ 10g^{7}+8g^{6}-15g^{5}-12g^{4}$

$\$	$\$
	$\$
	$\$

Textaufgaben zu den Grundrechenarten

Berechnen Sie das Produkt aus 6 und 7, reduzieren Sie die Zahl 39 um 48 und addieren Sie die zwei Ergebnisse!
Dividieren Sie die Summe von 7 und 33 durch die Differenz von 19 und 15!
Berechnen Sie das 8-fache von 7 und Subtrahieren Sie das Ergebnis aus der Zahl 23 um 15 erhöht!
Multiplizieren Sie den Quotient aus 91 und 7 mit der Zahl 26 auf 13 geteilt!

Antwort

33
10
-18
26

$\$	$\$
	$\$
	$\$

Grundrechenartenvorrang

$\ (-41)+99:(3\cdot 7-32)-(48:12+5)\cdot (-5)\$
$\ (+120):(2\cdot 7-36:9)-(35:5-3\cdot 2)\cdot (-4)$
$\ (7\cdot 3-56:2):(45:3-4\cdot 2)$

Antwort

$-5$
$16$
$-1$

Mathematrix: Werkzeuge/ Links

Direkte Proportionalität

(auch Schlussrechnung oder Dreisatz)

In EU produzierte im Jahr (365 Tage) 2016 eine Person durchschnittlich 6,5 Tonnen CO₂.

Wie viel war die Produktion pro Woche (7 Tage)?
Wie viele Tage hätte sie gebraucht, um 0,13 Tonnen zu produzieren?

Antwort

$\ x\approx 0{,}125\ \ t\quad$
$\ x=7,3\ Tage$

Mathematrix: Werkzeuge/ Links

Grundaufgaben der Prozentrechnung

Von wie vielen h sind 0,17 h 6510%?
Wie viel % von 0,17 h sind 6510 h?
Wie viel ist 0,17% von 6510 h?

Antwort

$\ x\approx 0{,}0026\ {\text{h}}\quad$
$\ x\approx 3830000\%\quad \$
$x\approx 11{,}1\ {\text{h}}\quad$

Mathematrix: Werkzeuge/ Links

Bruchkürzen

Kürzen Sie folgende Brüche!

$\ {\frac {21}{14}}=\qquad$
$\ {\frac {21}{12}}=\qquad$
$\ {\frac {12}{39}}=\qquad$
$\ {\frac {39}{52}}=\qquad$
$\ {\frac {33}{99}}=\qquad$

Antwort

$\ {\frac {3}{2}}\qquad$
$\ {\frac {7}{4}}\qquad$
$\ {\frac {4}{13}}\qquad$

$\ {\frac {3}{4}}\qquad$
$\ {\frac {1}{3}}\qquad$

Mathematrix: Werkzeuge/ Links

Kürzen mit Primfaktorzerlegung

$\ {\frac {6552}{4410}}=\qquad$
$\ {\frac {2184}{5544}}=\qquad$
$\ {\frac {56056}{32760}}=\qquad$

Antwort

$\ {\frac {52}{35}}\qquad$
$\ {\frac {13}{33}}\qquad$
$\ {\frac {77}{45}}$

Mathematrix: Werkzeuge/ Links

Erweitern

Erweitern Sie folgende Brüche mit der jeweils in Klammern angegebenen Zahl bzw. Variable!

$\ {\frac {9}{6}}=\ (4)\qquad$
$\ {\frac {12}{7}}=\ (5)\qquad$
$\ {\frac {5}{8}}=\ (8)\qquad$
$\ {\frac {11}{4}}=\ (6)\qquad$
$\ {\frac {5}{7}}=\ (m)\qquad$

Antwort

$\ {\frac {36}{24}}\qquad$
$\ {\frac {60}{35}}\qquad$
$\ {\frac {40}{64}}\qquad$
$\ {\frac {66}{24}}\qquad$
$\ {\frac {5m}{7m}}\qquad$

$\$	$\$
	$\ \$
	$\$

Gemischte Zahlen

Gemischte Zahl in unechten Bruch:

$5{\frac {2}{7}}\ \qquad \ 1{\frac {1}{6}}\ \qquad \ 9{\frac {8}{9}}\ \$
Unechten Bruch in gemischte Zahl
${\frac {447}{11}}\ \qquad \ {\frac {9}{7}}\ \qquad \ {\frac {35}{5}}\ \$
Subtraktion:
$5-{\frac {52}{7}}\ \qquad \ 1-{\frac {1}{6}}\ \qquad \ {\frac {143}{9}}-10\ \quad \ {\frac {16}{17}}-1\$

Antwort

$\ {\tfrac {37}{7}}\qquad$ $\ {\tfrac {7}{6}}\qquad$ $\ {\tfrac {89}{9}}$
$\ 40{\tfrac {7}{11}}\qquad$ $\ 1{\tfrac {2}{7}}\qquad$ $\ 7$
$\ -{\tfrac {17}{7}}\qquad$ $\ {\tfrac {5}{6}}\qquad$ $\ {\tfrac {53}{9}}\qquad$ $\ -{\tfrac {1}{17}}$

Mathematrix: Werkzeuge/ Links

Strich und Punkt Bruchrechnungen

$\ {\frac {11}{3}}:{\frac {8}{13}}\qquad \quad$
$\ {\frac {11}{3}}-{\frac {8}{13}}\$
$\ -{\frac {11}{13}}-{\frac {2}{13}}\qquad$
${\frac {11}{3}}\cdot {\frac {8}{13}}$

Antwort

$\textstyle \ {\frac {143}{24}}\qquad$
$\textstyle \ {\frac {119}{39}}\qquad$
$\textstyle \ -{\frac {13}{13}}(=-1)\qquad$
$\textstyle \ {\frac {88}{39}}\qquad$

$\$	$\$
	$\$
	$\$

Doppelbrüche

\quad

{\dfrac {\ {\frac {4}{3}}-{1}\ }{{\frac {5}{4}}-1}}

\quad

Antwort

$\textstyle 1{\frac {1}{3}}$

$\$	$\$
	$\$
	$\$

Umformen Grundwissen Gegenrechnungen

Berechnen Sie jeweils die unbekannte Variable!

$\ c+5347=2744\qquad$
$\ {\tfrac {k}{7}}=13\qquad$
$\ 6f=168\qquad$

$\ x-592=-5426\qquad$
$\ 58m=986\qquad$
$\ 51w=900\qquad$

Antwort

$c=-2603\qquad$
$k=91\qquad$
$f=28$

$x=-4834\qquad$
$\textstyle m={\tfrac {493}{29}}=17\qquad$
$w=17{\tfrac {11}{17}}\approx 17{,}65$

Mathematrix: Werkzeuge/ Links

Umformen einfache Kombinationen

Formen Sie auf die unbekannte Variable um!

7(3z+2)=9z-10

Antwort

Nicht vorhanden

$\$	$\$
	$\$
	$\$

Textaufgaben zu den Bruchrechnungen

In einem Staat mit ca. 9,702 Millionen EinwohnerInnen
und 1,32 Milliarden € Vermögen haben

99 Menschen $\textstyle \ {\frac {4}{15}}\$ des Vermögens ("Multimillionäre"),
noch 2640 Menschen $\textstyle \ {\frac {10}{33}}\$ des Vermögens ("Millionäre"),
noch 3,528 Millionen Menschen $\textstyle \ {\frac {4}{11}}\$ des Vermögens (Mittelschicht),
und die restlichen Menschen den Rest des Vermögens ("der Rest").

Antwort

$\textstyle {\frac {1}{98000}}\ {\text{der Menschen}}\qquad \ 352\ {\text{Millionen €}}\qquad$
$\textstyle {\frac {1}{3675}}\ {\text{der Menschen}}\qquad \ 400\ {\text{Millionen €}}\qquad$
$\textstyle {\frac {4}{11}}\ {\text{der Menschen}}\qquad \ 480\ {\text{Millionen €}}\qquad$
$\textstyle {\text{fast}}\ {\frac {7}{11}}\ {\text{der Menschen}}\qquad \ 88\ {\text{Millionen €}}\qquad$

Mathematrix: Werkzeuge/ Links

Indirekte Proportionalität

Nach heutigem Stand der Wissenschaft gibt es eine bestimmte Grenze am Energieverbrauch auf der Erde. Nehmen wir an, dass bei 7 Milliarden Menschen dies einen durchschnittlichen Energieverbrauch von 3 kWh pro Stunde ist. Wie viel wäre er bei 15 Milliarden Menschen?

Antwort

$1{,}4\ {\text{kWh}}\qquad$

Mathematrix: Werkzeuge/ Links

Einheiten und physikalische Größen

Ordnen Sie die passenden Einheiten zu den entsprechenden physikalischen Größen richtig zu:
Fläche eines Staates		$\qquad$	$\$ m²
Dauer einer Flugreise			$\$ km²
Dauer einer Schulpause			$\$ h
Fläche eines Zimmers			min $\quad$
Abstand zwischen den Augen $\quad$	$\quad$		$\$ s
Dauer eines Atemzugs			cm $\$

Antwort

Ordnen Sie richtig zu:
Fläche eines Staates	km²	$\qquad$	$\$ m²
Dauer einer Flugreise	h		$\$ km²
Dauer eine Schulpause	min		$\$ h
Fläche eines Zimmers	m²		$\$ min
Abstand zwischen den Augen $\quad$	cm $\quad$		s $\$
Dauer eines Atemzugs	s		cm $\$

Mathematrix: Werkzeuge/ Links

Einheiten ohne Hochzahl

Rechnen Sie um:

0,577 mm in m
577 km in dm
0,793 kg in mg
0,000783 s in min
0,0773 Tage in min

Antwort

$0{,}000577\ m\qquad$
$5770000\ km\qquad$
$793000\ mg\qquad$
$0{,}00001305\ min\qquad$
$111{,}312\ min$

Mathematrix: Werkzeuge/ Links

Einheiten mit Hochzahl

Rechnen Sie um:

447 dm³ in cm³
257 dm² in km²
311 mm² in m²
0,00335 cm³ in mm³
0,0257 dm³ in mm³

Antwort

$447000\ cm^{3}\qquad$
$0{,}00000257\ km^{2}\qquad$
$0{,}000311\ m^{2}\qquad$
$3{,}35\ mm^{3}$
$25700\ mm^{3}\qquad$

$\$	$\$
	$\$
	$\$

Formel Einsetzen in der ebenen Geometrie

Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche!

Eine Tür ist 21,5 dm hoch und 77 cm breit.
Der größte Abstand zwischen den Punkten eines Tellerrands ist 2,8 dm.
Die Länge eines Parallelogramms ist 0,34 m, die entsprechende Höhe 9 cm und die kürzere Seite 2,3 dm.

Antwort

$\ u=58{,}4\ dm\quad A=165{,}55\ dm^{2}\qquad$
$\ u=8{,}80\ dm\quad A=6{,}16\ dm^{2}\qquad$
$\ u=114\ cm\quad A=306\ cm^{2}\qquad$

$\$	$\$
	$\$
	$\$

Satz von Pythagoras

In der Figur seien a=12cm und c=169mm. Wie viel ist dann b?

Antwort

119\ \ {\text{mm}}

$\$	$\$
	$\$
	$\$

Lageparameter

Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln:

Das Modell DE, das die Verteilung des Vermögens in Deutschland ähnelt:

16

10

10

1

1

300

10

1

1

10

Das Modell GR, das die Verteilung des Vermögens in Griechenland ähnelt:

11

9

1

1

1

100

1

14

11

11

Berechnen Sie jeweils die Mittelwerte.

Antwort

DE: $D=36\qquad Med=10\qquad Mod=1\ \&\ 10\quad$
GR: $D=16\qquad Med=10\qquad Mod=1$

$\$	$\$
	$\$
	$\$

Lineare Funktion Diagramm

Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar.

Wie viel die Lebenserwartung ist, wenn eine Person 25 Zigaretten am Tag raucht.
Wie viel die Lebenserwartung ist, wenn eine Person 14 Zigaretten am Tag raucht.
Wie viele Zigaretten täglich geraucht werden, wenn die Lebenserwartung 68 Jahre ist.
Wie viele Zigaretten täglich geraucht werden, wenn die Lebenserwartung 65 Jahre ist.
Wie viel die Lebenserwartung für nicht-rauchende Personen ist.

Antwort

ca. 71 Jahre
ca. 77 Jahre
ca. 30 Zig./Tag
ca. 34 Zig./Tag
ca. 85 Jahre

$\$	$\$
	$\$
	$\$

Liniendiagramm

	Das Diagramm^[1] stellt die Konzentration von CO₂ (y-Achse) in Bezug auf die Zeit (x-Achse, Tausende Jahre in der Vergangenheit) dar. Lesen Sie vom Diagramm ab:
	Wie viel die Konzentration vor 50, 100 und 400 Tausende Jahre war. Wann die Konzentration 280 ppmv war. Wann die Konzentration 190 ppmv war.

Antwort

$\ {\text{ca. }}200\quad 250\quad {\text{bzw. }}280\quad {\text{ppmv}}\qquad$
$\ {\text{ca. }}400\ \ 320\ \ 240\ \ 130\ \ {\text{und }}\ 0\$ Tausende Jahre her.
$\ {\text{ca. }}360\ \ 345\ \ 270\ \ 260\ \ 165\ \ 150\ \ 40\ \ {\text{und }}\ 30\$ Tausende Jahre her.

$\$	$\$
	$\$
	$\$

Säulendiagramm

Lesen Sie vom Diagramm ab, wie viele SchülerInnen:

genau 3 Punkte

genau 5 Punkte

keine Punkte

höchstens 3 Punkte

mindestens 3 Punkte haben

mindestens 2 und höchstens 4 Punkte haben!

Antwort

$\$	$\$
	$\$
	$\$

Mittelwerte bei einem Säulendiagramm

Finden Sie die Mittelwerte im Diagramm!
Antwort

$\$	$\$
	$\$
	$\$

Kreisdiagramm

Zu welchen der folgenden Aussagen passen die folgenden Diagrammen?

Ein Stall hat 2 Ziegen, 3 Schafe, 8 Kühe, 2 Schweine und 1 Pferd.
Ein Kind hat 1 Kartenspiele, 2 Brettspiele, 2 Bälle, 3 Puppe und 1 Spielschwert.
In einer Schule gibt es 2 Lehrer für Mathematik, 1 für Englisch, 2 für Deutsch, 2 für Geographie und 1 für Musik.
Ein Bauernhof hat 18 Hühner, 1 Hahn, 3 Gänsen, 3 Kanarinen, 2 Katzen und 9 Enten.
In einem Tierheim gibt es 2 schwarze Katzen, 4 roten, 1 weißen, 8 dreifarbige und 1 schwarz-rot.
In einer Klasse sind 2 Personen aus Österreich, 2 aus Deutschland, 8 aus der Türkei, 2 aus Serbien und 2 aus Tschechien.
In einer Klasse wählen 3 Personen die Partei "Bild", 3 Personen die Partei "Welt", 3 die Partei "Nature", 6 die Partei "Grob" und 3 keine Partei.
Ein Haus hat 6 Schlafzimmer, 1 WCs, 1 Küche, 1 Wohnraum und 3 Badezimmer.

W
X
Y
Z

Antwort

W-g,\ X-d,\ Y-keiner,\ Z-e

$\$	$\$
	$\$
	$\$

Umformen in der ebenen Geometrie konkret

Der Umfang eines Kreises ist 12cm. Berechnen Sie die Fläche!

Antwort

$A\approx 11{,}46\ cm^{2}\qquad$

$\$	$\$
	$\ \$
	$\$

Bruchstrichrechnungen mit Primfaktorzerlegung

2{\frac {9}{28}}+{\frac {11}{63}}-1{\frac {5}{24}}

Antwort

${\frac {649}{504}}$

$\$	$\$
	$\$
	$\$

Ähnlichkeit von Figuren

In den Figuren werden zwei ähnliche Dreiecke dargestellt. Gegeben sind die Längen der folgenden Seiten: c=95 mm, b=7,4 cm, d=1,86 dm und f=14 cm. Wie lang sind die restlichen Seiten?

Antwort

$g\approx 239\ mm\qquad a\approx 56\ mm$

$\$	$\$
	$\$
	$\$

Prozentrechnung bei Wachstum und Abnahme

Das Gehalt einer Managerin war 650000€ und wurde nach eine Massenentlassung von Angestellten um 5,4% erhöht.

Berechnen sie das neue Gehalt!

Um wie viel € wurde das Gehalt erhöht?

Antwort

$685100\ {\text{€}}\qquad 35100\ {\text{€ mehr}}$

$\$	$\$
	$\$
	$\$

Umkehraufgaben der Prozentrechnung

Der pro Kopf Energieverbrauch in EU sei 3,6 kW und damit 1400% mehr als in Kongo. Wie viel ist er im Kongo?

Antwort

$0{,}24\ {\text{kW}}$

$\$	$\$
	$\$
	$\$

KESt., effektive Zinsen, Guthaben nach einem Jahr

Im Jahr 2001 war das Guthaben in einem Konto 80000€, der effektiver Zinssatz 1,05%.

Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 2002?
Antwort

$\$	$\$
	$\$
	$\$

Zinsen Umkehraufgaben

Im Jahr 2001 war das Guthaben in einem Konto 80000€, der effektiver Zinssatz 1,05%.

Wie viel war das Guthaben im Jahr 2000?
Antwort

$\$	$\$
	$\$
	$\$

Zinsrechnung

Im Jahr 2001 war das Guthaben in einem Konto 80000€, der effektiver Zinssatz 1,05%.

Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 2002?
Wie viel war das Guthaben im Jahr 2000?
Wie viel war das Guthaben im Jahr 2107?

Antwort

$G_{106}\approx 242069{,}28\ {\text{€}}$

$\$	$\$
	$\$
	$\$

Klasse 8

Textaufgaben zu den Grundrechenarten

Berechnen Sie das Produkt aus 6 und 7, reduzieren Sie die Zahl 39 um 48 und addieren Sie die zwei Ergebnisse!
Dividieren Sie die Summe von 7 und 33 durch die Differenz von 19 und 15!
Berechnen Sie das 8-fache von 7 und Subtrahieren Sie das Ergebnis aus der Zahl 23 um 15 erhöht!
Multiplizieren Sie den Quotient aus 91 und 7 mit der Zahl 26 auf 13 geteilt!

Antwort

33
10
-18
26

Mathematrix: Werkzeuge/ Links

Grundrechenartenvorrang

Antwort

Nicht vorhanden

Mathematrix: Werkzeuge/ Links

Vorrang mit Klammern in Klammern

\ -(-41+37)-[(-3\cdot 8-11):(+7)-(+4)]:(-9)+(+37)-(91:7-13)\cdot (-2)-(-11)\

Antwort

$\ 51$

$\$	$\$
	$\$
	$\$

Doppelbrüche

\quad

{\dfrac {\ {\frac {4}{3}}-{1}\ }{{\frac {5}{4}}-1}}

\quad

Antwort

$\textstyle 1{\frac {1}{3}}$

$\$	$\$
	$\$
	$\$

Bruchrechnungen und Vorrang

{\frac {16}{77}}:\left({\frac {3}{5}}-{\frac {45}{28}}:2{\frac {1}{4}}\right)-1{\frac {1}{11}}\cdot {\frac {5}{4}}

Antwort

$-{\frac {35}{11}}$

$\$	$\$
	$\$
	$\$

Textaufgaben zu den Bruchrechnungen

In einem Staat mit ca. 9,702 Millionen EinwohnerInnen
und 1,32 Milliarden € Vermögen haben

99 Menschen $\textstyle \ {\frac {4}{15}}\$ des Vermögens ("Multimillionäre"),
noch 2640 Menschen $\textstyle \ {\frac {10}{33}}\$ des Vermögens ("Millionäre"),
noch 3,528 Millionen Menschen $\textstyle \ {\frac {4}{11}}\$ des Vermögens (Mittelschicht),
und die restlichen Menschen den Rest des Vermögens ("der Rest").

Antwort

$\textstyle {\frac {1}{98000}}\ {\text{der Menschen}}\qquad \ 352\ {\text{Millionen €}}\qquad$
$\textstyle {\frac {1}{3675}}\ {\text{der Menschen}}\qquad \ 400\ {\text{Millionen €}}\qquad$
$\textstyle {\frac {4}{11}}\ {\text{der Menschen}}\qquad \ 480\ {\text{Millionen €}}\qquad$
$\textstyle {\text{fast}}\ {\frac {7}{11}}\ {\text{der Menschen}}\qquad \ 88\ {\text{Millionen €}}\qquad$

$\$	$\$
	$\$
	$\$

Kürzen mit Primfaktorzerlegung

$\ {\frac {6552}{4410}}=\qquad$
$\ {\frac {2184}{5544}}=\qquad$
$\ {\frac {56056}{32760}}=\qquad$

Antwort

$\ {\frac {52}{35}}\qquad$
$\ {\frac {13}{33}}\qquad$
$\ {\frac {77}{45}}$

$\$	$\$
	$\$
	$\$

Bruchstrichrechnungen mit Primfaktorzerlegung

2{\frac {9}{28}}+{\frac {11}{63}}-1{\frac {5}{24}}

Antwort

${\frac {649}{504}}$

Mathematrix: Werkzeuge/ Links

Textaufgaben Primfaktorzerlegung

Zwei Planeten und ihre Sonne befinden sich auf einer Gerade. Die Laufbahn der Planeten um ihrer Sonne dauert 11088 bzw. 56056 (von unseren) Tage. Wie lang dauert es bis die zwei Planeten und ihre Sonne sich wieder auf einer Gerade befinden?

Antwort

1009008 Tage

$\$	$\$
	$\$
	$\$

Direkte Proportionalität

(auch Schlussrechnung oder Dreisatz)

In EU produzierte im Jahr (365 Tage) 2016 eine Person durchschnittlich 6,5 Tonnen CO₂.

Wie viel war die Produktion pro Woche (7 Tage)?
Wie viele Tage hätte sie gebraucht, um 0,13 Tonnen zu produzieren?

Antwort

$\ x\approx 0{,}125\ \ t\quad$
$\ x=7,3\ Tage$

Mathematrix: Werkzeuge/ Links

Indirekte Proportionalität

Nach heutigem Stand der Wissenschaft gibt es eine bestimmte Grenze am Energieverbrauch auf der Erde. Nehmen wir an, dass bei 7 Milliarden Menschen dies einen durchschnittlichen Energieverbrauch von 3 kWh pro Stunde ist. Wie viel wäre er bei 15 Milliarden Menschen?

Antwort

$1{,}4\ {\text{kWh}}\qquad$

$\$	$\$
	$\$
	$\$

Vergleich direkter und indirekter Proportionalität

In Prato in Italien produzierten ChinesInnen (oft unter Druck) im Jahr 2018 billige Kleidung (oft um weniger als 1 € Stundenlohn und für mehr als 14 Stunden Arbeit pro Tag). In 21 Stunden produzieren 6 ArbeiterInnen Kleidung im Wert von 1400€.

Wie lang brauchen diese ArbeiterInnen um 210€ Wert Kleidung zu produzieren?

Wie lang brauchen 9 ArbeiterInnen um diese 1400€ Wert Kleidung zu produzieren?

Wie lang brauchen 8 ArbeiterInnen um 1750€ Wert Kleidung zu produzieren?

Antwort

3,15 h

14 h

19,6875 h

$\$	$\$
	$\$
	$\$

Grundaufgaben der Prozentrechnung

Von wie vielen h sind 0,17 h 6510%?

Wie viel % von 0,17 h sind 6510 h?

Wie viel ist 0,17% von 6510 h?

Antwort

\ x\approx 0{,}0026\ {\text{h}}\quad

\ x\approx 3830000\%\quad \

x\approx 11{,}1\ {\text{h}}\quad

Mathematrix: Werkzeuge/ Links

Prozentrechnung bei Wachstum und Abnahme

Das Gehalt einer Managerin war 650000€ und wurde nach eine Massenentlassung von Angestellten um 5,4% erhöht.

Berechnen sie das neue Gehalt!
Um wie viel € wurde das Gehalt erhöht?

Antwort

685100\ {\text{€}}\qquad 35100\ {\text{€ mehr}}

$\$	$\$
	$\$
	$\$

Kombinationsaufgaben der Prozentrechnung

Frankreich bezieht mehr als 70% seiner elektrischen Energie aus Kernkraftwerken. Ein (riesiges) Problem dabei ist der radioaktiver Müll, der für Hunderte bis Tausende Jahre gefährlich bleibt.^[2] Nehmen wir an, dass die Menge eines solchen Stoffes zwischen 1993 und 1994 um 4% gestiegen und zwischen 1994 und 1995 um weiter 5% auf 16,38 t gestiegen ist.

Wie viele t wäre sie ursprünglich?
Um wie viel Prozent wäre sie insgesamt gestiegen?

Antwort

$15\ {\text{t}}\qquad$
9,2% erhöht

$\$	$\$
	$\$
	$\$

Umsatzsteuer (USt.)

Der Bruttoverkaufspreis einer Ware ist 93€. Berechnen Sie den Nettoverkaufspreis, wenn die USt. 24% ist.

Antwort

NVP: 75 €

$\$	$\$
	$\$
	$\$

Rabatt

Der Verkaufspreis einer Ware nach einem Rabatt ist 836,6 €. Der Bruttoverkaufspreis war 890 €. Wie viel Prozent ist der Rabatt?

Antwort

6%

$\$	$\$
	$\$
	$\$

USt. und Rabatt Gegebener Endwert

Der Verkaufspreis einer Ware nach 20% Rabatt ist 88 €. Berechnen Sie den Netto- und Bruttoverkaufspreis , wenn die USt. 25% ist. Wie viel € ist der Rabatt bzw. die USt.?

Antwort

NVP: 88 €, BVP: 110 €, Rabatt: 22 €, USt.: 22 €

$\$	$\$
	$\$
	$\$

Prozentrechnung abstrakt

In den folgenden Beispielen gehen wir davon aus, dass es in der Bevölkerung so viele Männer gibt wie Frauen.

Der Anteil der Raucher unter der Bevölkerung ist 27,5%. Der Anteil der Raucher unter den Männern ist 35%. Wie viel ist der Anteil der Raucherinnen unter den Frauen?
Die Lebenserwartung der Bevölkerung ist 80 Jahre. Die Lebenserwartung der nicht-Raucher ist 82,4 Jahre. Wie viele Jahre weniger ist die Lebenserwartung der Rauchenden in Vergleich zu den nicht-Rauchenden Personen?
Wäre das Rauchen die einzige Erklärung für den Unterschied der Lebenserwartung zwischen den beiden Geschlechtern, wie viel Jahre wäre diese für Männer und für Frauen?
Welche Information ist noch notwendig, um den Einfluss des Rauchens auf den Lebenserwartungsunterschied zwischen den Geschlechtern genauer zu bestimmen?
Wenn wir letztere Information haben, was ist noch notwendig, um zu entscheiden, ob das Rauchen bei dieser Frage tatsächlich der einzige bestimmende Faktor ist? Vergleichen Sie ihre Ergebnisse mit tatsächlichen offiziellen Statistiken!

Antwort

$20\%\qquad$
8,7 Jahre
Männer ca. 79,4 Jahre, Frauen ca. 80,7 Jahre
Quoten in der höheren Altersstufe
Einfluss anderer Faktoren. Studien nach kann es großenteils (40%-60% des Unterschieds) stimmen.

$\$	$\$
	$\$
	$\$

Zahlenmengen

border="1" style="text-align:center; background: lightgrey; color: black; padding: 1em; font-size: 95%; margin: 1em "	Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\mathbb {N}$	$\mathbb {Z}$	$\mathbb {Q}$	$\mathbb {I}$	$\mathbb {R}$
$\textstyle {\frac {0{,}5}{\sqrt {0{,}0625}}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$\textstyle -{\frac {38}{3}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$\textstyle -{\frac {52}{1{,}3}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$\textstyle {\frac {\sqrt {169}}{13}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$\textstyle {\frac {\sqrt {-9}}{13}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
${28}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$-{\sqrt {(-25)(-4)}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
${\sqrt {18}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$

Antwort

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
$\textstyle {\frac {0{,}5}{\sqrt {0{,}0625}}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {38}{3}}$	✘	✘	✔	✘	✔
$\textstyle -{\frac {52}{1{,}3}}$	✘	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {169}}{13}}$	✔	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {-9}}{13}}$	✘	✘	✘	✘	✘
$28$	✔	✔	✔	✘	✔
$-{\sqrt {(-25)(-4)}}$	✘	✔	✔	✘	✔
${\sqrt {18}}$	✘	✘	✘	✔	✔

|

$\$	$\$
	$\$
	$\$

|}

Multiplikation von zwei Potenzen mit der gleichen Basis

${3^{-5}}\cdot {3^{6}}$
${b^{-2t}}\cdot {b^{-5t}}$

Antwort

$\ 3\qquad$
$\ b^{-7t}\qquad$

$\$	$\$
	$\$
	$\$

Division von zwei Potenzen mit der gleichen Basis

${\frac {b^{-3}}{b^{-5}}}$
${\frac {w^{-b}}{w^{-12}}}$

Antwort

$\ b^{2}\qquad$
$\ w^{12-b}$

$\$	$\$
	$\$
	$\$

Potenzen Erklärung

Warum ist $\textstyle \ s^{-1}={\frac {1}{s}}$ ?

Antwort

$\$	$\$
	$\$
	$\$

Aufgaben mit einer Klammer

Mathematrix: Aufgabensammlung/ Aufgaben mit einer Klammer

Antwort

Nicht vorhanden

$\$	$\$
	$\$
	$\$

Herausheben

Aufgaben mit 2 Klammern

Mathematrix: Aufgabensammlung/ Aufgaben mit 2 Klammern

Antwort

Nicht vorhanden

$\$	$\$
	$\$
	$\$

Herausheben

Faktorisieren Sie, so weit es mit natürlichen Zahlen geht:

$18\ b^{4}\ y^{3}\ n^{4}-12\ y^{7}n^{6}-30\ b^{8}y^{1}0n^{5}+6\ y^{3}\ n^{4}$

Antwort

$6\ y^{3}\ n^{4}(3\ b^{4}-2\ y^{4}n^{2}-5\ b^{8}y^{7}n+1)$

$\$	$\$
	$\$
	$\$

Binomische Formeln ausmultiplizieren

Multiplizieren Sie folgende binomische Formeln aus:

\ \left(12\ g^{2{,}5}+7\ g^{6{,}5}\right)^{2}\qquad

(4\ a^{4}-11\ a^{6})^{2}\quad

Antwort

144\ g^{5}+168\ g^{9}+49\ g^{13}\qquad

\ 16\ a^{8}-88\ a^{10}+121\ a^{12}

$\$	$\$
	$\$
	$\$

Binomische Formeln faktorisieren

Faktorisieren Sie folgende Terme:

\ 225\ v^{7}+360\ v^{12}+144\ v^{17}

4\ n^{4}-10\ n^{10}+6{,}25\ n^{16}

Antwort

\left(25\ v^{3{,}5}+12\ v^{8{,}5}\right)^{2}\qquad

(2\ n^{2}-2{,}5\ \ n^{8})^{2}

$\$	$\$
	$\$
	$\$

Binomische Formeln erkennen

Können folgende Ausdrücke als binomische Formeln faktorisiert werden? Wenn nicht, was könnte geändert werden?

\ 121\ r^{7}+330\ r^{12}+225\ r^{17}

\ 49\ c^{7}+14\ c^{11}+4\ c^{17}

Antwort

ja

Nein, 28 statt 14
und 12 statt 11

$\$	$\$
	$\$
	$\$

Das pascalsche Dreieck Binompotenzen

Multiplizieren Sie mit Hilfe des pascalschen Dreiecks folgendes Binom aus:

$\ (5b^{2}-7e)^{4}\quad$

Antwort

625\ b^{8}-3500\ b^{6}\ e+7350\ b^{4}\ e^{2}-6860\ b^{2}\ e^{3}+2401\ e^{4}

$\$	$\$
	$\$
	$\$

Bruchterme kürzen

Kürzen Sie folgenden Bruchterm:

${\frac {27x^{3}-18x^{2}+3x}{7x^{2}-4x+4x^{2}+1x}}$

Antwort

$\textstyle (3x-1)$

$\$	$\$
	$\$
	$\$

Bruchtermegleichungen

Finden Sie die Definitions- und die Lösungsmenge der folgenden Bruchtermegleichung

${\frac {4x^{2}-5x-2x^{2}+4x}{x^{2}+x}}-{\frac {2x}{x-1}}={\frac {2x+15}{x^{2}-1}}$

Antwort

$\mathbb {D} =\mathbb {R} \setminus \{-1,\ 0,\ 1\}\quad \mathbb {L} =\{-2\}$

$\$	$\$
	$\$
	$\$

Polynomdivision

Mathematrix: Aufgabensammlung/ Polynomdivision

Antwort

Nicht vorhanden

$\$	$\$
	$\$
	$\$

Umformen Grundwissen Gegenrechnungen

Mathematrix: Aufgabensammlung/ Umformen Grundwissen Gegenrechnungenn

Antwort

c=-2603\qquad

k=91\qquad

f=28

x=-4834\qquad

\textstyle m={\tfrac {493}{29}}=17\qquad

w=17{\tfrac {11}{17}}\approx 17{,}65

$\$	$\$
	$\$
	$\$

Umformen einfache Kombinationen

Formen Sie auf die unbekannte Variable um!

7(3z+2)=9z-10

Antwort

$z=-2$

$\$	$\$
	$\$
	$\$

Textaufgaben linearer Gleichungssysteme mit 2 Variablen

An einem Wohnblock gibt es 18 Wohnungen, manche haben 20 und der Rest 15 Steckdosen. Insgesamt haben sie 315 Steckdosen. Wie viele Wohnungen mit 15 bzw 20 Steckdosen gibt es?

Antwort

$9\ {\text{W mit 15 S.}}\qquad \ 9\ {\text{W.mit 20 S.}}\qquad$

$\$	$\$
	$\$
	$\$

Einsetzungsverfahren

Lösen Sie folgendes lineares Gleichungssystem mit

Hilfe des Einsetzungsverfahrens:

\ \left|\ {\begin{matrix}x+y=3\\-3x+5y=31\end{matrix}}\ \right|

Antwort

\textstyle (-2|5)

$\$	$\$
	$\$
	$\$

Gleichsetzungsverfahren

Lösen Sie folgendes lineares Gleichungssystem mit

Hilfe des Gleichsetzungsverfahrens:

\ \left|\ {\begin{matrix}x+y=-1\\-3x+2y=23\end{matrix}}\ \right|

Antwort

\textstyle (-5|4)

$\$	$\$
	$\$
	$\$

Additionsverfahren

Lösen Sie folgende lineare Gleichungssysteme mit

Hilfe des Eliminationsverfahrens:

\ \left|\ {\begin{matrix}2m-4c=8\\3m+5c=1\end{matrix}}\ \right|

\ \left|\ {\begin{matrix}3k-2g=-11\\-2k+5g=11\end{matrix}}\ \right|

Antwort

\textstyle (2|-1)

\textstyle (-3|1)

$\$	$\$
	$\$
	$\$

Lösungsmenge eines linearen Gleichungssystems

\left|\ {\begin{matrix}3x+2y=8\\4{,}5x+3y=8\end{matrix}}\ \right|

\ \left|\ {\begin{matrix}15x-9y=3\\x-0{,}2=0{,}6y\end{matrix}}\ \right|

\left|\ {\begin{matrix}-2x+2y=11\\3x+5y=24\end{matrix}}\ \right|

Antwort

Keine Lösung

\infty \

Lösungen

Eine Lösung

$\$	$\$
	$\$
	$\$

Lösbarkeit eines linearen Gleichungssystems mit 2 Variablen

\left|\ {\begin{matrix}3x+2y=8\\4{,}5x+3y=8\end{matrix}}\ \right|

\ \left|\ {\begin{matrix}15x-9y=3\\x-0{,}2=0{,}6y\end{matrix}}\ \right|

\left|\ {\begin{matrix}-2x+2y=11\\3x+5y=24\end{matrix}}\ \right|

Antwort

Nicht lösbar

Lösbar

Lösbar

$\$	$\$
	$\$
	$\$

Lineare Funktion Diagramm

Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar.

Wie viel die Lebenserwartung ist, wenn eine Person 25 Zigaretten am Tag raucht.
Wie viel die Lebenserwartung ist, wenn eine Person 14 Zigaretten am Tag raucht.
Wie viele Zigaretten täglich geraucht werden, wenn die Lebenserwartung 68 Jahre ist.
Wie viele Zigaretten täglich geraucht werden, wenn die Lebenserwartung 65 Jahre ist.
Wie viel die Lebenserwartung für nicht-rauchende Personen ist.

Antwort

ca. 71 Jahre
ca. 77 Jahre
ca. 30 Zig./Tag
ca. 34 Zig./Tag
ca. 85 Jahre

$\$	$\$
	$\$
	$\$

Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln

Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar.

Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?
Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

Antwort

$\ y=-{\frac {17x}{30}}+85$
x: Zig./Tag, y: Jahre, S: Jahre mal Tag/Zig.

$\$	$\$
	$\$
	$\$

Die Steigung und ihre Zusammenhänge

Zeigen Sie, dass die Steigung s einer linearen Funktion

\textstyle s={\frac {\Delta y}{\Delta x}}\

ist!

Antwort

hier klicken (Video)

$\$	$\$
	$\$
	$\$

Textaufgaben zu den linearen Funktionen

Ein Auto fährt von Paris nach der 311 km entfernten Stadt Brüssels mit 72 km/h durchschnittlicher Geschwindigkeit.

Geben Sie zuerst den Zusammenhang zwischen Zeit und Abstand von Brüssels als lineare Funktion an!
Wie lang dauert die Fahrt?
Wie weit von Brüssels und wie weit von Paris entfernt
befindet sich das Auto nach 24 min?
Wie viel kg ist der CO₂ Ausstoß nach 24 min,
wenn 7 kg nach 40 km ausgestoßen werden?

Antwort

}

$\$	$\$
	$\$
	$\$

Ähnlichkeit von Figuren

In den Figuren werden zwei ähnliche Dreiecke dargestellt. Gegeben sind die Längen der folgenden Seiten: c=95 mm, b=7,4 cm, d=1,86 dm und f=14 cm. Wie lang sind die restlichen Seiten?

Antwort

$g\approx 239\ mm\qquad a\approx 56\ mm$

Mathematrix: Werkzeuge/ Links

Zusammengesetzte Figuren

Drücken Sie den dunklen Flächeninhalt durch die Länge a der Seite des gleichseitigen Dreiecks aus!

Antwort

A=\ {\tfrac {\sqrt {3}}{4}}a^{2}-\left({\tfrac {a}{2}}\right)^{2}

$\$	$\$
	$\ \$
	$\$

Formel Einsetzen in der ebenen Geometrie

Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche!

Eine Tür ist 21,5 dm hoch und 77 cm breit.

Der größte Abstand zwischen den Punkten eines Tellerrands ist 2,8 dm.

Die Länge eines Parallelogramms ist 0,34 m, die entsprechende Höhe 9 cm und die kürzere Seite 2,3 dm.

Antwort

\ u=58{,}4\ dm\quad A=165{,}55\ dm^{2}\qquad

\ u=8{,}80\ dm\quad A=6{,}16\ dm^{2}\qquad

\ u=114\ cm\quad A=306\ cm^{2}\qquad

$\$	$\$
	$\$
	$\$

Umformen in der ebenen Geometrie konkret

Der Umfang eines Kreises ist 12cm. Berechnen Sie die Fläche!

Antwort

A\approx 11{,}46\ cm^{2}\qquad

Mathematrix: Werkzeuge/ Links

Umformen in der ebenen Geometrie abstrakt

Begründen Sie, ob in einem gleichseitigen Dreieck mit Fläche A die Seite a mit der Formel: $\textstyle {a={\sqrt {A\cdot {\tfrac {4}{\sqrt {3}}}\ }}}$ berechnet werden kann.

Antwort

$a={\sqrt {\tfrac {4A}{\sqrt {3}}}}\left(=2{\sqrt {\tfrac {A}{\sqrt {3}}}}={\sqrt {A\cdot {\tfrac {4}{\sqrt {3}}}\ }}\right)$

$\$	$\$
	$\$
	$\$

Satz von Pythagoras

In der Figur seien a=12cm und c=169mm. Wie viel ist dann b?
Ein Schiff wird mit dem Dock über eine 229cm lange Rampe verbunden, der Hohenunterschied der beiden Enden der Rampe ist 6dm. Wie viel ist die horizontale Entfernung der beiden Enden der Rampe?

Antwort

$119\ \ {\text{mm}}$
$221\ \ {\text{cm}}$

$\$	$\$
	$\$
	$\$

Geometrie Beweise

Mit Hilfe der Figur beweisen Sie den Satz von Pythagoras.

Antwort

hier

$\$	$\$
	$\$
	$\$

Formel Einsetzen in der Raumgeometrie

Der Abstand vom Mittelpunkt bis am Rand der Basis eines Tipis (indianisches Zelt) ist 39 dm, seine Höhe 2,8 m. Wie viel ist der Umfang der Basis, der Mantel, der Boden und das Volumen des Zeltes?

Antwort

$U\approx 245\ dm\qquad M\approx 58{,}8\ m^{2}\qquad$ $B\approx 47{,}8\ m^{2}\qquad V\approx 44{,}6\ m^{3}$

$\$	$\$
	$\ \$
	$\$

Umformen in der Raumgeometrie konkret

Die Oberfläche eines Balles ist 1256,64 cm². Wie viel ist sein Volumen?

Antwort

$V\approx 4189\ cm^{3}$

$\$	$\$
	$\ \$
	$\$

Umformen in der Raumgeometrie abstrakt

Leo gibt für die Berechnung der Seite a der Basis einer quadratischen Pyramide mit Volumen V, deren Höhe h so viel wie diese Seite der Basis ist, folgende Formel an:

$\qquad a={\sqrt[{3}]{3V}}$

Überprüfen Sie, ob die Formel richtig ist und, falls nicht, geben Sie die richtige Formel an!

Antwort

Formel stimmt

$\$	$\$
	$\ \$
	$\$

Lageparameter

Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln:

Das Modell DE, das die Verteilung des Vermögens in Deutschland ähnelt:

16

10

10

1

1

300

10

1

1

10

Das Modell GR, das die Verteilung des Vermögens in Griechenland ähnelt:

11

9

1

1

1

100

1

14

11

11

Berechnen Sie jeweils die Mittelwerte.

Antwort

DE: $D=36\qquad Med=10\qquad Mod=1\ \&\ 10\quad$
GR: $D=16\qquad Med=10\qquad Mod=1$

$\$	$\$
	$\$
	$\$

Vergleichen von Mittelwerten

Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln:

Das Modell DE, das die Verteilung des Vermögens in Deutschland ähnelt:

16

10

10

1

1

300

10

1

1

10

Das Modell GR, das die Verteilung des Vermögens in Griechenland ähnelt:

11

9

1

1

1

100

1

14

11

11

Berechnen Sie jeweils die Mittelwerte.
Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?

Antwort

DE: Verteilung ungleichmäßig
GR: Verteilung möglicherweise gleichmäßig

$\$	$\$
	$\$
	$\$

Mittelwerte Argumentationsaufgaben

Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln:

Das Modell DE, das die Verteilung des Vermögens in Deutschland ähnelt:

16

10

10

1

1

300

10

1

1

10

Das Modell GR, das die Verteilung des Vermögens in Griechenland ähnelt:

11

9

1

1

1

100

1

14

11

11

Berechnen Sie jeweils die Mittelwerte.
Vergleichen Sie jeweils Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
- Sind die Verteilungen gleich- oder ungleichmäßig? Was ist ihrer Unterschied?
- Es wurde damals oft in Zeitungen geschrieben, dass der "deutsche Steuerzahler" den Griechen "Geld gibt", obwohl Griechen "reicher sind". Welcher Lagerparameter wird in dieser Aussage verglichen? Ist dieser Vergleich wirklich aussagekräftig? Wo ist das Geld wirklich gelangen also wem hat tatsächlich der "Steuerzahler" das Geld gegeben? (Dazu kann man insbesondere dieses Unterkapitel in Wikipedia lesen)

Antwort

Beide Verteilungen sind ziemlich ungleichmäßig, allerdings ist der Median in Griechenland nicht so weit vom Durchschnitt. In den Zeitungen wurde der Median verglichen (der ist in GR größer), was völlig daneben ist (der Durchschnitt in DE ist viel höher als in GR). "Griechen" sind nicht "reicher" als "Deutsche", sondern das Vermögen in Deutschland wird ziemlich ungleichmäßiger als in Griechenland verteilt.
Das (allerdings geliehene) Geld gelangt zu den Geldgebern in Deutschland. Das führt zu einer Verstärkung der Ungleichmäßigkeit in DE (und allerdings auch in GR).

$\$	$\$
	$\$
	$\$

Säulendiagramm

Lesen Sie vom Diagramm ab, wie viele SchülerInnen:

genau 3 Punkte

genau 5 Punkte

keine Punkte

höchstens 3 Punkte

mindestens 3 Punkte haben

mindestens 2 und höchstens 4 Punkte haben!

Antwort

\ 2,\ \ 6,\ \ 1,\ \ 5,\ \ 18,\ \ {\text{und }}7\ {\text{Punkte}}

Mathematrix: Werkzeuge/ Links

Mittelwerte bei einem Säulendiagramm

Finden Sie die Mittelwerte im Diagramm!

Antwort

D\approx 4{,}19\ {\text{Pun./Sch.}},\ Med=5,\ Mod=5

Mathematrix: Werkzeuge/ Links

Lineare Funktion Diagramm

Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar.
Antwort

ca. 71 Jahre
ca. 77 Jahre
ca. 30 Zig./Tag
ca. 34 Zig./Tag
ca. 85 Jahre

Mathematrix: Werkzeuge/ Links

Liniendiagramm

	Das Diagramm^[3] stellt die Konzentration von CO₂ (y-Achse) in Bezug auf die Zeit (x-Achse, Tausende Jahre in der Vergangenheit) dar. Lesen Sie vom Diagramm ab:
	Wie viel die Konzentration vor 50, 100 und 400 Tausende Jahre war. Wann die Konzentration 280 ppmv war. Wann die Konzentration 190 ppmv war.

Antwort

$\ {\text{ca. }}200\quad 250\quad {\text{bzw. }}280\quad {\text{ppmv}}\qquad$
$\ {\text{ca. }}400\ \ 320\ \ 240\ \ 130\ \ {\text{und }}\ 0\$ Tausende Jahre her.
$\ {\text{ca. }}360\ \ 345\ \ 270\ \ 260\ \ 165\ \ 150\ \ 40\ \ {\text{und }}\ 30\$ Tausende Jahre her.

Mathematrix: Werkzeuge/ Links

Klasse 9

Textaufgaben zu den Grundrechenarten

Berechnen Sie das Produkt aus 6 und 7, reduzieren Sie die Zahl 39 um 48 und addieren Sie die zwei Ergebnisse!

Dividieren Sie die Summe von 7 und 33 durch die Differenz von 19 und 15!

Berechnen Sie das 8-fache von 7 und Subtrahieren Sie das Ergebnis aus der Zahl 23 um 15 erhöht!

Multiplizieren Sie den Quotient aus 91 und 7 mit der Zahl 26 auf 13 geteilt!

Antwort

33

10

-18

26

Mathematrix: Werkzeuge/ Links

Doppelbrüche

\quad

{\dfrac {\ {\frac {4}{3}}-{1}\ }{{\frac {5}{4}}-1}}

\quad

Antwort

$\textstyle 1{\frac {1}{3}}$

Mathematrix: Werkzeuge/ Links

Bruchrechnungen und Vorrang

{\frac {16}{77}}:\left({\frac {3}{5}}-{\frac {45}{28}}:2{\frac {1}{4}}\right)-1{\frac {1}{11}}\cdot {\frac {5}{4}}

Antwort

$-{\frac {35}{11}}$

Mathematrix: Werkzeuge/ Links

Textaufgaben zu den Bruchrechnungen

In einem Staat mit ca. 9,702 Millionen EinwohnerInnen
und 1,32 Milliarden € Vermögen haben

99 Menschen

\textstyle \ {\frac {4}{15}}\

des Vermögens ("Multimillionäre"),

noch 2640 Menschen

\textstyle \ {\frac {10}{33}}\

des Vermögens ("Millionäre"),

noch 3,528 Millionen Menschen

\textstyle \ {\frac {4}{11}}\

des Vermögens (Mittelschicht),

und die restlichen Menschen den Rest des Vermögens ("der Rest").

Wie viel Geld besitzt jede Gruppe?

Fleißaufgabe: Welcher Anteil der Bevölkerung (als gekürzte Bruch) gehört zu jeder Gruppe
Vergleichen Sie diese Daten mit Daten aus ihrem eigenen Staat!

Antwort

\textstyle {\frac {1}{98000}}\ {\text{der Menschen}}\qquad \ 352\ {\text{Millionen €}}\qquad

\textstyle {\frac {1}{3675}}\ {\text{der Menschen}}\qquad \ 400\ {\text{Millionen €}}\qquad

\textstyle {\frac {4}{11}}\ {\text{der Menschen}}\qquad \ 480\ {\text{Millionen €}}\qquad

\textstyle {\text{fast}}\ {\frac {7}{11}}\ {\text{der Menschen}}\qquad \ 88\ {\text{Millionen €}}\qquad

Mathematrix: Werkzeuge/ Links

Kürzen mit Primfaktorzerlegung

\ {\frac {6552}{4410}}=\qquad

\ {\frac {2184}{5544}}=\qquad

\ {\frac {56056}{32760}}=\qquad

Antwort

\ {\frac {52}{35}}\qquad

\ {\frac {13}{33}}\qquad

\ {\frac {77}{45}}

Mathematrix: Werkzeuge/ Links

Bruchstrichrechnungen mit Primfaktorzerlegung

2{\frac {9}{28}}+{\frac {11}{63}}-1{\frac {5}{24}}

Antwort

${\frac {649}{504}}$

Mathematrix: Werkzeuge/ Links

Vorsilben und Gleitkommadarstellung

In den folgenden Beispielen finden Sie die unbekannte Hochzahl (x).

A) 37 MW = 0,0037 · 10^x cW

\qquad

B) 4,3 nm = 0,000043 · 10^x dm

C) 0,0334 THz = 33400 · 10^x μHz

\quad

D) 0,88 μHz = 8800000 · 10^x GHz

E) 67000 dm³ = 0,0067 · 10^x km³

\quad

F) 3300 cm² = 0,033 · 10^x m²

Antwort

A) 12 $\quad$ B) −3
C) 11 $\quad$ $\quad$ D) -22
E) −5 $\quad$ $\quad$ F) -2

$\$	$\$
	$\$
	$\$

Zahlenmengen

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\mathbb {N}$	$\mathbb {Z}$	$\mathbb {Q}$	$\mathbb {I}$	$\mathbb {R}$
$\textstyle {\frac {0{,}5}{\sqrt {0{,}0625}}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$\textstyle -{\frac {38}{3}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$\textstyle -{\frac {52}{1{,}3}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$\textstyle {\frac {\sqrt {169}}{13}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$\textstyle {\frac {\sqrt {-9}}{13}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
${28}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
$-{\sqrt {(-25)(-4)}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$
${\sqrt {18}}$	$\quad$	$\quad$	$\quad$	$\quad$	$\quad$

Antwort

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
$\textstyle {\frac {0{,}5}{\sqrt {0{,}0625}}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {38}{3}}$	✘	✘	✔	✘	✔
$\textstyle -{\frac {52}{1{,}3}}$	✘	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {169}}{13}}$	✔	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {-9}}{13}}$	✘	✘	✘	✘	✘
$28$	✔	✔	✔	✘	✔
$-{\sqrt {(-25)(-4)}}$	✘	✔	✔	✘	✔
${\sqrt {18}}$	✘	✘	✘	✔	✔

Mathematrix: Werkzeuge/ Links

Multiplikation von zwei Potenzen mit der gleichen Basis

${3^{-5}}\cdot {3^{6}}$
${b^{-2t}}\cdot {b^{-5t}}$

Antwort

$\ 3\qquad$
$\ b^{-7t}\qquad$

Mathematrix: Werkzeuge/ Links

Division von zwei Potenzen mit der gleichen Basis

${\frac {b^{-3}}{b^{-5}}}$
${\frac {w^{-b}}{w^{-12}}}$

Antwort

$\ b^{2}\qquad$
$\ w^{12-b}$

Mathematrix: Werkzeuge/ Links

Potenzen Erklärung

Warum ist $\textstyle \ s^{-1}={\frac {1}{s}}$ ?

Antwort

Mathematrix: Werkzeuge/ Links

Potenzen mit negativer Hochzahl

Schreiben Sie folgende Terme ohne Bruch auf!

$\ \ {\frac {3}{r^{2r-4}}}=\quad$
$\ \ {\frac {11\ b^{4-5w}}{b^{3w}}}=\quad$
$\ \ 5\cdot {\frac {1}{5^{z}}}=\quad$

Antwort

$\ 3\cdot r^{4-2r}\qquad$
$\ 11\cdot b^{4-8w}\qquad$
$\ 5^{1-z}\qquad$

$\$	$\$
	$\$
	$\$

Komplexe Beispiele mit Potenzzahlen

Vereinfachen Sie!

${\left(m^{50 \over 3}\right)}^{9 \over 10}$
${\sqrt[{15}]{u^{-6}}}^{\ 5}$
$\left(\left(m^{5 \over 4}\right)^{6}\cdot {\sqrt[{11}]{m^{6}}}\cdot m^{-8}\right)^{33}$
${\dfrac {\sqrt[{4}]{{\Bigl (}k^{7 \over 3}{\Bigr )}^{12}}}{k^{4} \over k^{-3}}}$

Antwort

$m^{15}$
$u^{-2}\left(={\frac {1}{u^{2}}}\right)$
$b^{\frac {3}{2}}\left(={\sqrt {m^{3}}}\right)$
$1$

$\$	$\$
	$\$
	$\$

Aufgaben mit einer Klammer

Mathematrix: Aufgabensammlung/ Aufgaben mit einer Klammer

Antwort

Nicht vorhanden

Mathematrix: Werkzeuge/ Links

Herausheben

Aufgaben mit 2 Klammern

Mathematrix: Aufgabensammlung/ Aufgaben mit 2 Klammern

Antwort

Nicht vorhanden

Mathematrix: Werkzeuge/ Links

Herausheben

Faktorisieren Sie, so weit es mit natürlichen Zahlen geht:

$18\ b^{4}\ y^{3}\ n^{4}-12\ y^{7}n^{6}-30\ b^{8}y^{1}0n^{5}+6\ y^{3}\ n^{4}$

Antwort

$6\ y^{3}\ n^{4}(3\ b^{4}-2\ y^{4}n^{2}-5\ b^{8}y^{7}n+1)$

Mathematrix: Werkzeuge/ Links

Umformen Grundwissen Gegenrechnungen

Mathematrix: Aufgabensammlung/ Umformen Grundwissen Gegenrechnungenn

Antwort

c=-2603\qquad

k=91\qquad

f=28

x=-4834\qquad

\textstyle m={\tfrac {493}{29}}=17\qquad

w=17{\tfrac {11}{17}}\approx 17{,}65

Mathematrix: Werkzeuge/ Links

Umformen einfache Kombinationen

Formen Sie auf die unbekannte Variable um!

7(3z+2)=9z-10

Antwort

$z=-2$

Mathematrix: Werkzeuge/ Links

Komplexe Umformungen

{\sqrt {p}}+c_{L}\cdot {\frac {m\cdot v^{2}}{2\cdot k_{B}\cdot T}}-{\frac {t-s}{w-z}}=2,2

Formen Sie diese Formel auf z, m, v, T, p, t, s, k_B, c_L um!

Antwort

\quad z=w-{\frac {(t-s)\cdot {2\cdot k_{B}\cdot T}}{{\sqrt {p}}\cdot {2\cdot k_{B}\cdot T}+c_{L}\cdot {m\cdot v^{2}}-4{,}4\cdot {k_{B}\cdot T}}}

\quad m=\left(2,2-{\sqrt {p}}+{\frac {t-s}{w-z}}\right)\cdot {\frac {2\cdot k_{B}\cdot T}{c_{L}\cdot v^{2}}}

\quad v={\sqrt {\left(2,2-{\sqrt {p}}+{\frac {t-s}{w-z}}\right)\cdot {\frac {2\cdot k_{B}\cdot T}{c_{L}\cdot m}}\ \ }}

\quad {T}={\frac {w-z}{\left(2,2\cdot (w-z)-{\sqrt {p}}\cdot (w-z)+{t-s}\right)}}\cdot {\frac {2\cdot k_{B}}{v^{2}\cdot c_{L}\cdot m}}

\quad p=\left(2,2-c_{L}\cdot {\frac {m\cdot v^{2}}{2\cdot k_{B}\cdot T}}+{\frac {t-s}{w-z}}\ \right)^{2}

\quad {t}=\left({\sqrt {p}}+c_{L}\cdot {\frac {m\cdot v^{2}}{2\cdot k_{B}\cdot T}}-2,2\right)\cdot {w-z}+s

\quad {s}=t-\left({\sqrt {p}}+c_{L}\cdot {\frac {m\cdot v^{2}}{2\cdot k_{B}\cdot T}}-2,2\right)\cdot {w-z}

\quad {k_{B}}={\frac {w-z}{\left(2,2\cdot (w-z)-{\sqrt {p}}\cdot (w-z)+{t-s}\right)}}\cdot {\frac {2\cdot T}{v^{2}\cdot c_{L}\cdot m}}

\quad c_{L}=\left(2,2-{\sqrt {p}}+{\frac {t-s}{w-z}}\right)\cdot {\frac {2\cdot k_{B}\cdot T}{m\cdot v^{2}}}

$\$	$\$
	$\$
	$\$

Textaufgaben linearer Gleichungssysteme mit 2 Variablen

An einem Wohnblock gibt es 18 Wohnungen, manche haben 20 und der Rest 15 Steckdosen. Insgesamt haben sie 315 Steckdosen. Wie viele Wohnungen mit 15 bzw 20 Steckdosen gibt es?

Antwort

$9\ {\text{W mit 15 S.}}\qquad \ 9\ {\text{W.mit 20 S.}}\qquad$

Mathematrix: Werkzeuge/ Links

Einsetzungsverfahren

Lösen Sie folgendes lineares Gleichungssystem mit

Hilfe des Einsetzungsverfahrens:

\ \left|\ {\begin{matrix}x+y=3\\-3x+5y=31\end{matrix}}\ \right|

Antwort

\textstyle (-2|5)

Mathematrix: Werkzeuge/ Links

Gleichsetzungsverfahren

Lösen Sie folgendes lineares Gleichungssystem mit

Hilfe des Gleichsetzungsverfahrens:

\ \left|\ {\begin{matrix}x+y=-1\\-3x+2y=23\end{matrix}}\ \right|

Antwort

\textstyle (-5|4)

Mathematrix: Werkzeuge/ Links

Additionsverfahren

Lösen Sie folgende lineare Gleichungssysteme mit

Hilfe des Eliminationsverfahrens:

\ \left|\ {\begin{matrix}2m-4c=8\\3m+5c=1\end{matrix}}\ \right|

\ \left|\ {\begin{matrix}3k-2g=-11\\-2k+5g=11\end{matrix}}\ \right|

Antwort

\textstyle (2|-1)

\textstyle (-3|1)

Mathematrix: Werkzeuge/ Links

Lösungsmenge eines linearen Gleichungssystems

\left|\ {\begin{matrix}3x+2y=8\\4{,}5x+3y=8\end{matrix}}\ \right|

\ \left|\ {\begin{matrix}15x-9y=3\\x-0{,}2=0{,}6y\end{matrix}}\ \right|

\left|\ {\begin{matrix}-2x+2y=11\\3x+5y=24\end{matrix}}\ \right|

Antwort

Keine Lösung

\infty \

Lösungen

Eine Lösung

Mathematrix: Werkzeuge/ Links

Lösbarkeit eines linearen Gleichungssystems mit 2 Variablen

\left|\ {\begin{matrix}3x+2y=8\\4{,}5x+3y=8\end{matrix}}\ \right|

\ \left|\ {\begin{matrix}15x-9y=3\\x-0{,}2=0{,}6y\end{matrix}}\ \right|

\left|\ {\begin{matrix}-2x+2y=11\\3x+5y=24\end{matrix}}\ \right|

Antwort

Nicht lösbar

Lösbar

Lösbar

Mathematrix: Werkzeuge/ Links

Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln

Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar.

Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?
Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

Antwort

$\ y=-{\frac {17x}{30}}+85$
x: Zig./Tag, y: Jahre, S: Jahre mal Tag/Zig.

Mathematrix: Werkzeuge/ Links

Darstellungen der linearen Funktion

Wie lautet die implizite und die Vektorform der
linearen Funktion $y=bx-5$ ?
Wie lautet die explizite und die Vektorform der
linearen Funktion $2\ x-q\ y=w$ ?
Wie lautet die explizite und die implizite Form der
linearen Funktion ${\tbinom {x}{y}}={\tbinom {2}{-q}}t+{\tbinom {3}{4}}$ ?
Berechnen Sie den Winkel zwischen den Geraden der zweiten und der dritten Funktion!

Antwort

$b\ x-y-5=0,\quad {\tbinom {x}{y}}={\tbinom {1}{b}}t+{\tbinom {0}{-5}}$
$y={\tfrac {2}{q}}\ x-{\tfrac {w}{q}},\quad {\tbinom {x}{y}}={\tbinom {q}{2}}t+{\tbinom {0}{-{\tfrac {w}{q}}}}$
$y=-{\tfrac {q\ x}{2}}+{\tfrac {3q}{2}}+4,\quad q\ x+y-3\ q-4=0$
$90^{\circ }$ (normal)

$\$	$\$
	$\$
	$\$

Schnittpunkte von Funktionen in einem Diagramm

Im Bild sehen wir eine Polynomfunktion g(x) (gestrichelt),
drei quadratische Funktionen c(x), d(x) und e(x)
(zwei Kurven c und e nach oben und eine Kurve d nach
unten) und zwei lineare Funktionen h(x) und f(x)
(Gerade f nach unten rechts und Gerade h nach
oben rechts). Lesen Sie vom Diagramm ab:

Die Lösungen (Nullstellen) jeder Funktion.
Den y-Achsenabschnitt jeder Funktion.
Die Lösungen der Gleischungssysteme,
die aus folgenden Funktionen bestehen:

i) h und f

\quad

ii) g und d

\quad

iii) c und f

iv)e und h

\quad

v) g und f

\quad

vi) c und d

Antwort

f:{1,6}, h:{6}, g:{−2,6; 2,2; 4,5}, e:{}, c:{1,1; 6}, d{−2,2; 6}.
f:{2,5}, g:{2,5}, h:{−4}, e:{0,6}, c:{2}, d{1,2}.
i) {(3|−2)}
ii) {(−2,6|−0,5), (1,2|1,6), (4,6|0,8)}
iii) {(3|−2), (−1|4)} $\qquad$ iv){}
v) {(0|2,5), (3|−2), (3,6|−3)}
vi) {(0,3|1,4), (6|0)}

$\$	$\$
	$\$
	$\$

Schnittpunkte von Funktionen in einem Text

Gegeben sind die Funktionen
$g(x)={\frac {14-3x}{7}}$ $\quad f(x)={\sqrt {5}}-\pi x\quad$ $q(x)=-0{,}0625x^{2}+1$
$p(x)=5x^{2}-2{,}5x\quad \ h(x)=-3x^{2}+3x-2$

Berechnen Sie die Lösungen (Nullstellen) jeder Funktion!
Lesen Sie den y-Achsenabschnitt jeder Funktion ab!
Finden Sie, ob der Punkt P:(1| ${\sqrt {5}}-\pi$ )

zu mancher der Funktionen gehört!

Lesen Sie die Steigung der beiden Geraden ab!
Berechnen Sie die Lösungen der folgenden Gleichungssysteme

i) g und f, ii) h und q, iii) p und g

Antwort

g:{ $\textstyle {\frac {108}{3}}$ }, f:{ ${\tfrac {\sqrt {5}}{\pi }}$ }, q{0; 1,6}, p:{±0,75}, h:{}.
g:{2}, f:{ ${\sqrt {5}}$ }, q:{1}, p:{0}, h{−2}.
ja nur für f
g: s= $\textstyle -{\frac {3}{7}}$ $\ \ \$ f: s= $-\pi$
i) { $\textstyle \left({\frac {7({\sqrt {5}}-2)}{7\pi -3}}|{\frac {14\pi -3{\sqrt {5}}}{7\pi -3}}\right)$ } $\qquad$ ii) { }
iii) { $\textstyle \left({\frac {{\sqrt {8681}}+29}{140}}{\big |}{\frac {1873-3{\sqrt {8681}}}{980}}\right)$ , $\textstyle \ \left({\frac {-{\sqrt {8681}}+29}{140}}{\big |}{\frac {1873+3{\sqrt {8681}}}{980}}\right)$ } $\qquad$

$\$	$\$
	$\$
	$\$

Die quadratische Gleichung

Lösen Sie folgende quadratische Gleichungen:

$4y^{2}+4y+1=0$
$-5k^{2}-7k+6=0$
$-p^{2}-25=0$

Antwort

$y={\tfrac {1}{2}}$
$k_{1}={\tfrac {3}{5}}\quad k_{2}=-2$
$\mathbb {L} =\emptyset$

$\$	$\$
	$\$
	$\$

Umkehrfunktionen mit Umformen finden

Finden Sie die Umkehrfunktion:

$\ n(y)=\tan({{\sqrt[{5}]{y}}-5\ })\ +\pi$

Antwort

$y(n)=({\arctan(n-\pi )+5})^{5}$

$\$	$\$
	$\$
	$\$

Definition von Sinus Kosinus und Tangens

Geben Sie Sinus, Kosinus und Tangens des kleinsten

Winkels im folgenden rechtwinkeligen Dreieck an!

Wie groß sind die entsprechenden Werte, wenn
e=5 cm und m=1 dm sind?

Antwort

$\sin \varepsilon ={\frac {e}{m}}={\frac {1}{2}}\quad \cos \varepsilon ={\frac {f}{m}}={\frac {\sqrt {3}}{2}}\quad \tan \varepsilon ={\frac {e}{f}}={\frac {\sqrt {3}}{3}}$

$\$	$\$
	$\ \$
	$\$

Radiant

Rechnen Sie in Grad ° (Winkelmaß) um!
a)

\ 7\pi \ rad

, B)

\ {\frac {7\pi }{6}}\ rad

, C)

\ 1{,}5\ rad

, D)

\ {\frac {7}{9\pi }}\ rad

, E)

\ 420\ rad

Rechnen Sie in Radiants (Bogenmaß) um
A)

\ 15^{\circ }

, B)

\ 0{,}8^{\circ }

, C)

\ 7\pi ^{\circ }

, D)

\ {\frac {430}{7\pi }}^{\circ }

, E)

\ 560^{\circ }

Sind folgende Winkel mehr oder weniger als ein Halbkreis?
Wo befinden sie sich im Einheitskreis?
A)

\ 90^{\circ }

, B)

\ 180^{\circ }

, C)

\ 1\ rad

, D)

\ 7{,}6\ rad

, E)

\ 730^{\circ }

Antwort

A)

\ 1260^{\circ },\quad

B)

\ 210^{\circ },\quad

C)

\ ca.\ 85{,}9^{\circ },\quad

D)

\ ca.\ 14{,}2^{\circ },\quad

E)

\ ca.\ 24100^{\circ }\quad

A)

\ {\tfrac {\pi }{12}}\ rad,\quad

B)

\ \ {\tfrac {\pi }{225}}rad,\quad

C)

\ {\tfrac {7\pi ^{2}}{360}}\ rad,\quad

D)

\ {\tfrac {43}{252}}\ rad,\quad

E)

{\tfrac {14\pi }{9}}\ rad\quad

A) 1.Q

\quad

B) zwischen 2. und 3. Q

\quad

C) 1.Q

\quad

D) 1.Q aber mehr als Halbkreis!

\quad

E) 1.Q aber mehr als Halbkreis!

$\$	$\$
	$\ \$
	$\$

Direkte Anwendung des Sinus und des Kosinussatzes

Berechnen sie die Diagonale

d_{2}

des

abgebildeten Deltoids, wenn die Seite $a=4{,}8\ cm$ , die Diagonale $d_{1}=7{,}6\ cm$
und der Winkel zwischen $a$ und $b\ \angle ab=129^{\circ }$ sind.

Antwort

$d_{2}\approx 3{,}53\ cm$

$\$	$\$
	$\$
	$\$

Vermessungsaufgaben

Vom Gipfel eines 2411 m hohen Berges wird der Abstand
zwischen zwei Türmen in einem Tal gemessen,
die sich beide auf einer Höhe von 356 m befinden.
Zum ersten Turm wird der Tiefenwinkel

\alpha =37^{\circ }

gemessen
und nach Schwenken des Messgerätes um den Horizontalwinkel

\gamma =69^{\circ }

zum anderen Turm wird dieser unter dem Tiefenwinkel

\beta =43^{\circ }

gesehen. Wie viel ist der Abstand zwischen den Türmen?
Machen Sie eine saubere Skizze für die Berechnung!

Antwort

d\approx 2826\ m

$\$	$\$
	$\$
	$\$

Vektorrechnungen

Der Vektor ${\vec {a}}\$ ist der Vektor vom Punkt D
zum Punkt G. Berechnen Sie:

$3{\vec {a}}-2{\vec {u}}$
$|a|\$ und den Betrag des Vektors u
$3{\vec {a}}\cdot 2{\vec {u}}$
Den Winkel zwischen ${\vec {a}}\$ und ${\vec {u}}$
Die Länge des Vektors ${\vec {c}}=3{\vec {v}}_{1}-2{\vec {a}}\$ (genau und gerundet)
Die Steigung der tragende Gerade des Vektors ${\vec {a}}$
Zerlegen Sie den Vektor ${\vec {a}}$ zu seinen Komponenten

Antwort

$\ {\tbinom {-16}{-1}}$
$\ |a|=5,|u|=2{\sqrt {5}}$
$\ 24$
$\ 79{,}70^{\circ }$
$\ {\sqrt {409}}\approx 20{,}3$
$\ 0{,}75$
$\ a_{x}=-4\ ,a_{y}=-3$

$\$	$\$
	$\ \$
	$\$

Die quadratische Gleichung

Lösen Sie folgende quadratische Gleichungen:

$4y^{2}+4y+1=0$
$-5k^{2}-7k+6=0$
$-p^{2}-25=0$

Antwort

$y={\tfrac {1}{2}}$
$k_{1}={\tfrac {3}{5}}\quad k_{2}=-2$
$\mathbb {L} =\emptyset$

Mathematrix: Werkzeuge/ Links

Quadratische Gleichung Textaufgaben

Ein PKW fährt von Belgrad ins 311 km entfernte Sarajevo.
Nachdem er 235 km zurückgelegt hat, begegnet
ihm ein LKW, der 69 Minuten später von Sarajevo nach
Belgrad abgefahren ist und in der Stunde 20 km
weniger zurücklegt als der PKW.

Berechnen Sie die Geschwindigkeit des PKWs.
Nach wie viel Zeit treffen die Wagen einander?

Antwort

$v_{1}\approx 32{,}5\ {\text{oder }}125{,}8$
$t_{1}\approx 7{,}23\ {\text{oder }}1{,}87\ h$

$\$	$\$
	$\$
	$\$

Klasse 10

Multiplikation von zwei Potenzen mit der gleichen Basis

${3^{-5}}\cdot {3^{6}}$
${b^{-2t}}\cdot {b^{-5t}}$

Antwort

$\ 3\qquad$
$\ b^{-7t}\qquad$

Mathematrix: Werkzeuge/ Links

Division von zwei Potenzen mit der gleichen Basis

${\frac {b^{-3}}{b^{-5}}}$
${\frac {w^{-b}}{w^{-12}}}$

Antwort

$\ b^{2}\qquad$
$\ w^{12-b}$

Mathematrix: Werkzeuge/ Links

Potenzen Erklärung

Warum ist $\textstyle \ s^{-1}={\frac {1}{s}}$ ?

Antwort

Mathematrix: Werkzeuge/ Links

Potenzen mit negativer Hochzahl

Schreiben Sie folgende Terme ohne Bruch auf!

$\ \ {\frac {3}{r^{2r-4}}}=\quad$
$\ \ {\frac {11\ b^{4-5w}}{b^{3w}}}=\quad$
$\ \ 5\cdot {\frac {1}{5^{z}}}=\quad$

Antwort

$\ 3\cdot r^{4-2r}\qquad$
$\ 11\cdot b^{4-8w}\qquad$
$\ 5^{1-z}\qquad$

Mathematrix: Werkzeuge/ Links

Komplexe Beispiele mit Potenzzahlen

Vereinfachen Sie!

${\left(m^{50 \over 3}\right)}^{9 \over 10}$
${\sqrt[{15}]{u^{-6}}}^{\ 5}$
$\left(\left(m^{5 \over 4}\right)^{6}\cdot {\sqrt[{11}]{m^{6}}}\cdot m^{-8}\right)^{33}$
${\dfrac {\sqrt[{4}]{{\Bigl (}k^{7 \over 3}{\Bigr )}^{12}}}{k^{4} \over k^{-3}}}$

Antwort

$m^{15}$
$u^{-2}\left(={\frac {1}{u^{2}}}\right)$
$b^{\frac {3}{2}}\left(={\sqrt {m^{3}}}\right)$
$1$

Mathematrix: Werkzeuge/ Links

Umformen Grundwissen Gegenrechnungen

Berechnen Sie jeweils die unbekannte Variable!

$\ c+5347=2744\qquad$
$\ {\tfrac {k}{7}}=13\qquad$
$\ 6f=168\qquad$

$\ x-592=-5426\qquad$
$\ 58m=986\qquad$
$\ 51w=900\qquad$

Antwort

$c=-2603\qquad$
$k=91\qquad$
$f=28$

$x=-4834\qquad$
$\textstyle m={\tfrac {493}{29}}=17\qquad$
$w=17{\tfrac {11}{17}}\approx 17{,}65$

Mathematrix: Werkzeuge/ Links

Umformen einfache Kombinationen

Formen Sie auf die unbekannte Variable um!

$7(3z+2)=9z-10$

Antwort

z=-2

Mathematrix: Werkzeuge/ Links

Komplexe Umformungen

${\sqrt {p}}+c_{L}\cdot {\frac {m\cdot v^{2}}{2\cdot k_{B}\cdot T}}-{\frac {t-s}{w-z}}=2,2$
Formen Sie diese Formel auf z, m, v, T, p, t, s, k_B, c_L um!

Antwort

$\quad z=w-{\frac {(t-s)\cdot {2\cdot k_{B}\cdot T}}{{\sqrt {p}}\cdot {2\cdot k_{B}\cdot T}+c_{L}\cdot {m\cdot v^{2}}-4{,}4\cdot {k_{B}\cdot T}}}$
$\quad m=\left(2,2-{\sqrt {p}}+{\frac {t-s}{w-z}}\right)\cdot {\frac {2\cdot k_{B}\cdot T}{c_{L}\cdot v^{2}}}$
$\quad v={\sqrt {\left(2,2-{\sqrt {p}}+{\frac {t-s}{w-z}}\right)\cdot {\frac {2\cdot k_{B}\cdot T}{c_{L}\cdot m}}\ \ }}$
$\quad {T}={\frac {w-z}{\left(2,2\cdot (w-z)-{\sqrt {p}}\cdot (w-z)+{t-s}\right)}}\cdot {\frac {2\cdot k_{B}}{v^{2}\cdot c_{L}\cdot m}}$
$\quad p=\left(2,2-c_{L}\cdot {\frac {m\cdot v^{2}}{2\cdot k_{B}\cdot T}}+{\frac {t-s}{w-z}}\ \right)^{2}$
$\quad {t}=\left({\sqrt {p}}+c_{L}\cdot {\frac {m\cdot v^{2}}{2\cdot k_{B}\cdot T}}-2,2\right)\cdot {w-z}+s$
$\quad {s}=t-\left({\sqrt {p}}+c_{L}\cdot {\frac {m\cdot v^{2}}{2\cdot k_{B}\cdot T}}-2,2\right)\cdot {w-z}$
$\quad {k_{B}}={\frac {w-z}{\left(2,2\cdot (w-z)-{\sqrt {p}}\cdot (w-z)+{t-s}\right)}}\cdot {\frac {2\cdot T}{v^{2}\cdot c_{L}\cdot m}}$
$\quad c_{L}=\left(2,2-{\sqrt {p}}+{\frac {t-s}{w-z}}\right)\cdot {\frac {2\cdot k_{B}\cdot T}{m\cdot v^{2}}}$

Mathematrix: Werkzeuge/ Links

Exponentialfunktion und Logarithmus

Wie viel ist die gesuchte Variable in den folgenden Aufgaben?

$e^{\lambda }={\frac {1}{2}}\quad$
$\ln m=-3\quad$
${\text{log}}_{3}v=0\quad$
$7^{\alpha }=3^{3}$
$3^{8}=e^{4\lambda }$

Antwort

$\lambda =\ln 0{,}5\approx -0{,}693\quad$
$m=e^{-3}=0{,}0498\quad$
$v=3^{0}=1\quad$
$\alpha =\log _{7}27=1{,}694$
$\lambda =\ln 9\approx 2{,}19$

$\$	$\$
	$\ \$
	$\$

Arbeiten mit Logarithmen

Zerlegen Sie folgenden Ausdruck unter
Verwendung der Logarithmusregeln in den
möglichst einfachsten Logarithmanden.
$\ln \left(e^{e}{\frac {b^{c}}{b+m}}\right)^{\sqrt {2}}$
Fassen Sie folgenden Ausdruck unter
Verwendung der Logarithmusregeln in
einen Logarithmanden.
$4-d\log _{v}6+4\log _{v}e$

Antwort

$\ {\sqrt {2}}(e+c\ln b-\ln(b+m))\qquad$
$\ \log _{v}{\tfrac {v^{4}e^{4}}{6^{d}}}$

$\$	$\$
	$\$
	$\$

Folgen

Die Größe vier Geschwister stellt eine geometrische Folge dar.
Vom kleinsten aus heißen sie Andi, Lisa, Tom und Aria.
Aria ist $182\ cm$ groß, Tom 5% kleiner.

Wie viel Prozent größer als Tom ist Aria?
Wie viel Prozent kleiner als Tom ist Lisa?
Wie groß ist Andi?

Antwort

$\approx 5{,}26\%$
$5\%$
$\approx 156\ cm$

$\$	$\$
	$\ \$
	$\$

Textaufgaben zu linearen Gleichungssystemen

Drei verschiedene Schulen (Alpha, Sigma und Omega) machen eine Exkursion nach London. Wenn wir aus der Summe der Fünffachen der Personen aus Sigma und des Doppelten aus Omega die Personen aus Alpha subtrahieren, dann wäre das Ergebnis 700 (Personen). Sigma fliegt und stoßt damit 450 kg CO₂ für 200€ pro Person aus, Alpha fährt mit dem Zug und stoßt damit 40 kg CO₂ für 300€ pro Person aus und Omega fährt mit dem Bus und stoßt damit 36 kg CO₂ für 240€ pro Person aus. Für alle Schulen zusammengerechnet sind die Kosten 120 Tausend € und der CO₂ Ausstoß 67,4 t. Wie viele Personen aus jeder Schule fahren?

Antwort

$\alpha :\ 200\$ Personen, $\sigma :\ 120\$ Personen, $\omega :\ 150\$ Personen

$\$	$\$
	$\ \$
	$\$

Polynomfunktionen Diagramm

In den folgenden Diagrammen bestimmen Sie den
Grad der dargestellten Polynomfunktion, die Anzahl
ihrer Lösungen, ihr Monotonieverhalten in den
verschiedenen Intervallen, das Vorzeichen der
Koeffizienten der Potenz mit dem höchsten Grad und
wenn möglich den Wert des y-Achsenabschnitts!

A
B
C

D
E
F

G
H
I

Antwort

$\$	$\$
	$\$
	$\$

Schnittpunkte von Funktionen in einem Diagramm

Im Bild sehen wir eine Polynomfunktion g(x) (gestrichelt),
drei quadratische Funktionen c(x), d(x) und e(x)
(zwei Kurven c und e nach oben und eine Kurve d nach
unten) und zwei lineare Funktionen h(x) und f(x)
(Gerade f nach unten rechts und Gerade h nach
oben rechts). Lesen Sie vom Diagramm ab:

Die Lösungen (Nullstellen) jeder Funktion.
Den y-Achsenabschnitt jeder Funktion.
Die Lösungen der Gleischungssysteme,
die aus folgenden Funktionen bestehen:

i) h und f

\quad

ii) g und d

\quad

iii) c und f

iv)e und h

\quad

v) g und f

\quad

vi) c und d

Antwort

f:{1,6}, h:{6}, g:{−2,6; 2,2; 4,5}, e:{}, c:{1,1; 6}, d{−2,2; 6}.
f:{2,5}, g:{2,5}, h:{−4}, e:{0,6}, c:{2}, d{1,2}.
i) {(3|−2)}
ii) {(−2,6|−0,5), (1,2|1,6), (4,6|0,8)}
iii) {(3|−2), (−1|4)} $\qquad$ iv){}
v) {(0|2,5), (3|−2), (3,6|−3)}
vi) {(0,3|1,4), (6|0)}

Mathematrix: Werkzeuge/ Links

Schnittpunkte von Funktionen in einem Text

Gegeben sind die Funktionen
$g(x)={\frac {14-3x}{7}}$ $\quad f(x)={\sqrt {5}}-\pi x\quad$ $q(x)=-0{,}0625x^{2}+1$
$p(x)=5x^{2}-2{,}5x\quad \ h(x)=-3x^{2}+3x-2$

Berechnen Sie die Lösungen (Nullstellen) jeder Funktion!
Lesen Sie den y-Achsenabschnitt jeder Funktion ab!
Finden Sie, ob der Punkt P:(1| ${\sqrt {5}}-\pi$ )

zu mancher der Funktionen gehört!

Lesen Sie die Steigung der beiden Geraden ab!
Berechnen Sie die Lösungen der folgenden Gleichungssysteme

i) g und f, ii) h und q, iii) p und g

Antwort

g:{ $\textstyle {\frac {108}{3}}$ }, f:{ ${\tfrac {\sqrt {5}}{\pi }}$ }, q{0; 1,6}, p:{±0,75}, h:{}.
g:{2}, f:{ ${\sqrt {5}}$ }, q:{1}, p:{0}, h{−2}.
ja nur für f
g: s= $\textstyle -{\frac {3}{7}}$ $\ \ \$ f: s= $-\pi$
i) { $\textstyle \left({\frac {7({\sqrt {5}}-2)}{7\pi -3}}|{\frac {14\pi -3{\sqrt {5}}}{7\pi -3}}\right)$ } $\qquad$ ii) { }
iii) { $\textstyle \left({\frac {{\sqrt {8681}}+29}{140}}{\big |}{\frac {1873-3{\sqrt {8681}}}{980}}\right)$ , $\textstyle \ \left({\frac {-{\sqrt {8681}}+29}{140}}{\big |}{\frac {1873+3{\sqrt {8681}}}{980}}\right)$ } $\qquad$

Mathematrix: Werkzeuge/ Links

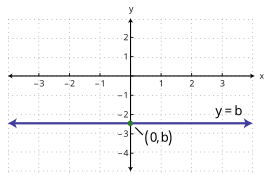
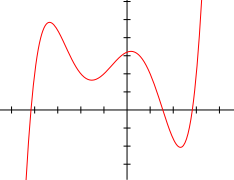
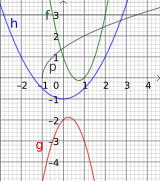
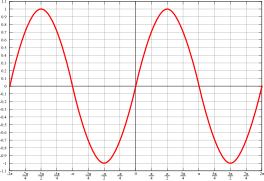
Funktionserkennung in Diagramm

Welches der folgenden Diagrammen stellt was dar?

A) lineare Funktion, B) Polynomfunktion 2. Grades
C) Wurzelfunktion, D) Polynomfunktion 3. Grades
E) Polynomfunktion 4. Grades, F) Sinusfunktion
G) Kosinusfunktion, H) quadratische Funktion,
K) (natürlichen) Logarithmusfunktion, L) $\textstyle {\frac {a}{x}}$
M) Exponentialfunktion, N) Umkehrfunktionenpaar

1
2
3

4
5
6

7
8
9

10
11
12

13
14
15

Antwort

1 → G, 2 → E, 3→ D, 4 → B H
5 → F,6 → B H, 7 → K M N, 8 → A
9 → C, 10 → B H, 11 → L, 12 → A
13 → M, 14 → K, 15 → C D N

$\$	$\$
	$\$
	$\$

Funktionsdiagramme Eigenschaften erkennen

Wählen Sie das jeweils richtige Diagramm und
beantworten Sie die entsprechende Frage!

Wie viel ist der y-Achsenabschnitt bei jedem Diagramm?
Wie viel ist die Steigung der linearen Funktionen?
$ax^{2}+bx+c\$ $ax^{2}+bx+c\$ ist die quadratische Funktion.
- Bei welcher Funktion ist a negativ bzw. positiv?
$ae^{b\ x}\$ ist die exponentielle Funktion.
${\frac {a}{x}}\$ ist die indirekte Proportionalität.
Bei welcher Funktion ist a negativ bzw. positiv?
In welchen Intervallen sind die quadratischen und die linearen
Funktionen, die Sinusfunktionen bzw die indirekte
Proportionalität steigend bzw. fallend?
Gibt es in irgendeinem Diagramm eine Funktion und
ihre Umkehrfunktion?
Gibt es in irgendeinem Diagramm eine Funktion und
ihre auf der y-Achse gespeigelte Funktion? Was gilt
in diesem Fall für f(x) und ihre Spiegelfunktion f^s(x)?

Antwort

$\$	$\$
	$\$
	$\$

Funktionserkennung in Text

Im Folgenden finden wir verschiedene Diagramme, Formel und Namen von Funktionen als auch Textaufgaben darüber. Welche sind die richtigen Kombinationen für jede Textaufgabe? Mit Hilfe der Textaufgaben finden Sie die Werte der Parameter a und b in der dem Text entsprechenden Formel.
Texte TA (Text A) Fanny will feststellen, ob ihre Katze einen freien Fall überlebt und lässt sie aus einem 8 m hohen Turm mit einer 3 m/s² festen Beschleunigung Fallen. TB (Text B) Die Bevölkerung in Deutschland ist ca. 82 Millionen und wird jede Jahrzehnte um 2,3% weniger. TC (Text C) Bei der Schwingung einer Feder ist die maximale Ablenkung 3 cm, eine vollständige Wiederholung braucht 350 ms.	TD (Text D) Ein Baum ist 3,5 m groß und wächst pro Woche um 5 cm. TE (Text E) Eine 1,8 dm große Kerze schmilzt jede Stunde um 3 cm. TF (Text F) Wenn wir auf einen Nagel eine Kraft ausüben, ist der Druck desto größer, je kleiner die Fläche A an der Spitze des Nagels ist aber je größer die Kraft F ist. (Hier a und b durch entsprechende Symbole ersetzten) TG (Text G) Ein Bakterienkultur verdreifacht sich jede Stunde. Am Anfang gibt es 5 Bakterien.
Diagramme DA (Diagramm A) DB (Diagramm B) DC (Diagramm C) DD (Diagramm D) DE (Diagramm E) DF (Diagramm F)	DG (Diagramm G) DH (Diagramm H) DI (Diagramm I) Funktionsnamen NA: (Name A) lineare, NB:(Name B) quadratische, NC: (Name C) exponentielle, ND: (Name D) logarithmische, NE: (Name E) Potenzfunktion 3. Grades, NF: (Name F) Sinusfunktion, NG: (Name G) Wurzelfunktion, NH:(Name H) indirekte Proportionalität. Formeln FA: (Formel A) $\ y=a\ x+b\quad$ FB: (Formel B) $\ y=a\ e^{b\ x}\quad$ FC: (Formel C) $\ y=a\tan b\ x\quad$ FD: (Formel D) $\textstyle \ y={\frac {a}{b}}\quad$ FE: (Formel E) $\ \textstyle \ y=a\sin {\frac {1}{2\pi b}}x\quad$ FF: (Formel F) $\ y=a\ x^{2}+b\quad$ FG: (Formel G) $\ y=a\ x^{3{,}2}+b\quad$

Antwort

$\$	$\$
	$\$
	$\$

Umkehrfunktionen mit Umformen finden

Finden Sie die Umkehrfunktion:

$\ n(y)=\tan({{\sqrt[{5}]{y}}-5\ })\ +\pi$

Antwort

y(n)=({\arctan(n-\pi )+5})^{5}

Mathematrix: Werkzeuge/ Links

Definition von Sinus Kosinus und Tangens

Geben Sie Sinus, Kosinus und Tangens des kleinsten
Winkels im folgenden rechtwinkeligen Dreieck an!

Wie groß sind die entsprechenden Werte, wenn
e=5 cm und m=1 dm sind?

Antwort

\sin \varepsilon ={\frac {e}{m}}={\frac {1}{2}}\quad \cos \varepsilon ={\frac {f}{m}}={\frac {\sqrt {3}}{2}}\quad \tan \varepsilon ={\frac {e}{f}}={\frac {\sqrt {3}}{3}}

Mathematrix: Werkzeuge/ Links

Trigonometrische Umkehrfunktionen

\textstyle {\frac {77}{85}}

Wie viel ist der Kosinus?
Wie groß ist der Winkel?
Wie groß ist die Hypotenuse eines rechtwinkeligen
Dreiecks, wenn die Gegenkathete des Winkels
mit Sinus $\textstyle {\frac {77}{85}}\$ 11 cm ist?

Schreiben Sie eine Formel für den Winkel $\phi$ in Bezug auf die Seiten m und e auf! Wie groß ist der Winkel $\phi$ im Bild, wenn m=37 cm und e=300 mm sind?
Die Steigung eines Winkels ist 20%. Wie groß ist der Winkel?

Antwort

$\cos ={\frac {36}{85}}$
$\theta \approx 64{,}94^{\circ }$
${\tfrac {85}{7}}\approx 12{,}14\ cm$
$\phi =\arccos \left({\tfrac {e}{m}}\right)\approx 35{,}82^{\circ }$
$ca.\ 11{,}31^{\circ }$

$\$	$\$
	$\ \$
	$\$

Pythagoras Satz in Trigonometrie Abstrakt

Beweisen Sie mit Hilfe der Definitionen der trigonometrischen
Funktionen in einem allgemeinen Dreieck! $\quad {\tfrac {a}{\sin \alpha }}={\tfrac {b}{\sin \beta }}={\tfrac {c}{\sin \gamma }}$

Antwort

$\$	$\$
	$\$
	$\$

Pythagoras Satz in Trigonometrie Konkret

Die kleinere Kathete eines rechtwinkeligen Dreiecks ist 119 vm,
die größere 1,2 m. Wie viel genau ist der Tangens, der Sinus und der
Kosinus des kleinsten Winkels? Wie groß ist dieser Winkel? Wie
viel ist der Kosinus des anderen nicht rechten Winkels und wie
groß der andere Winkel?

Antwort

\tan \alpha ={\tfrac {11{,}9}{12}}\quad \sin \alpha =cos\beta ={\tfrac {119}{169}}\quad \cos \alpha ={\tfrac {120}{169}}

\alpha \approx 44{,}76^{\circ }\quad \beta \approx 45{,}24^{\circ }

$\$	$\$
	$\$
	$\$

Einheitskreis und trigonometrische Funktionen

Mit Hilfe des Einheitskreises finden sie zumindest vier Winkel, deren

i) Sinus

-{\tfrac {\sqrt {2}}{2}}

ist.

\quad

ii) Kosinus

{\tfrac {\sqrt {2}}{2}}

ist.

Antwort

$\$	$\$
	$\ \$
	$\$

Radiant

Rechnen Sie in Grad ° (Winkelmaß) um!
a) $\ 7\pi \ rad$ , B) $\ {\frac {7\pi }{6}}\ rad$ , C) $\ 1{,}5\ rad$ , D) $\ {\frac {7}{9\pi }}\ rad$ , E) $\ 420\ rad$
Rechnen Sie in Radiants (Bogenmaß) um
A) $\ 15^{\circ }$ , B) $\ 0{,}8^{\circ }$ , C) $\ 7\pi ^{\circ }$ , D) $\ {\frac {430}{7\pi }}^{\circ }$ , E) $\ 560^{\circ }$
Sind folgende Winkel mehr oder weniger als ein Halbkreis?
Wo befinden sie sich im Einheitskreis?
A) $\ 90^{\circ }$ , B) $\ 180^{\circ }$ , C) $\ 1\ rad$ , D) $\ 7{,}6\ rad$ , E) $\ 730^{\circ }$

Antwort

A) $\ 1260^{\circ },\quad$ B) $\ 210^{\circ },\quad$ C) $\ ca.\ 85{,}9^{\circ },\quad$ D) $\ ca.\ 14{,}2^{\circ },\quad$ E) $\ ca.\ 24100^{\circ }\quad$
A) $\ {\tfrac {\pi }{12}}\ rad,\quad$ B) $\ \ {\tfrac {\pi }{225}}rad,\quad$ C) $\ {\tfrac {7\pi ^{2}}{360}}\ rad,\quad$ D) $\ {\tfrac {43}{252}}\ rad,\quad$ E) ${\tfrac {14\pi }{9}}\ rad\quad$
A) 1.Q $\quad$ B) zwischen 2. und 3. Q $\quad$ C) 1.Q $\quad$ D) 1.Q aber mehr als Halbkreis! $\quad$ E) 1.Q aber mehr als Halbkreis!

Mathematrix: Werkzeuge/ Links

Baumdiagramm

In einer Urne gibt es 4 schwarze und 7 rote Kugeln. Wir ziehen drei mal zufällig
jeweils eine Kugel, ohne sie zurückzulegen. Wie viel ist die Wahrscheinlichkeit, dass:

alle 3 Kugel rot sind?
alle 3 Kugel schwarz sind?
die ersten zwei schwarz und die dritte rot sind?
wir zwei schwarze und eine rote Kugel ziehen?
wir zwei rote und eine schwarze Kugel ziehen?
das Letztere passiert, wenn wir doch zurücklegen?
alle drei schwarz sind, wenn wir doch zurücklegen?

Antwort

$\ {\frac {7}{33}}\quad$
$\ {\frac {4}{165}}\quad$
$\ {\frac {14}{165}}\quad$
$\ {\frac {14}{55}}\quad$
$\ {\frac {28}{55}}\quad$
$\ {\frac {588}{1331}}\quad$
$\ {\frac {64}{1331}}\quad$

$\$	$\$
	$\ \$
	$\$

Satz von Bayes konkretes Beispiel

In einem Studentenheim wohnen 35 Studenten und 48 Studentinnen. 80% der Studenten und ein Drittel der Studentinnen fahren zum Lebensmittel-Einkauf mit dem Auto, der Rest mit dem Fahrrad oder zu Fuss. Eine Person aus dem Heim fährt gerade zum Einkauf mit dem Auto. Wie viel ist Wahrscheinlichkeit, dass sie weiblich ist?

Antwort

${\frac {4}{11}}=36{,}{\overline {36}}\%$

$\$	$\$
	$\$
	$\$

Satz von Bayes abstraktes Beispiel

Nach den optimistischsten Voraussagen über die Menschen-verursachte Erderwärmung, ist die Wahrscheinlichkeit, dass die Temperatur bis 2050 „nur“höchstens 1,5°C steigt, 18%. Wenn wir allerdings keine Massnahmen treffen, ist sie nur 5%. Die Wahrscheinlichkeit, dass wir solche Massnahmen treffen, wenn wir die politische Situation^[4] und das Benehmen der Erdbevölkerung^[5] in Anbetracht nehmen, liegt bei 24% ^[6]. Nehmen wir an, wir leben schon im Jahr 2050 und die Temperaturerhöhung ist tatsächlich weniger als 1,5°C geblieben. Wie viel ist die Wahrscheinlichkeit, das dies geschehen ist, obwohl wir keine Massnahmen getroffen haben?

↑ Vereinfachung von https://commons.wikimedia.org/wiki/File:Carbon_Dioxide_800kyr.svg
↑ Neben dem radioaktiven Müll, der unter Anderem früher legal und später illegal ins Meer geworfen wurde, gibt es auch andere Gefahren durch solche Kraftwerke, wie bei Unfällen, z.B. in Tschernobyl und in Fukushima
↑ Vereinfachung von https://commons.wikimedia.org/wiki/File:Carbon_Dioxide_800kyr.svg
↑ mit der immer steigenden Repräsentation von rechten Parteien, die nicht gerade selten die Erderwärmung verleugnen
↑ mit dem ständig steigenden Konsum sogar in entwickelten Ländern mit einem hohen Lebensniveau
↑ das ist jetzt nur eine Vermutung

Antwort

$\ 21{,}{\dot {1}}\%$

$\$	$\$
	$\$
	$\$

Klasse 11

Ableitung von Potenzfunktionen

Berechnen Sie die Ableitungsfunktion der folgenden Funktionen. Wie viel ist die Ableitung der jeweiligen Funktion an der Stelle 2?

$g(n)={\tfrac {4}{7}}\ n^{7}\quad$
$v(y)=y^{\pi }\quad$
$u(g)=0{,}4\ g^{5}$

Antwort

$\ 4\,n^{6}$
$\pi \ y^{\pi -1}\quad$
$2g^{4}$

$\$	$\$
	$\ \$
	$\$

Ableitung von Potenzfunktionen komplex

Berechnen Sie die Ableitung der folgenden Funktionen.

$a(c)={\sqrt {b}}\left({\frac {1}{c}}\right)^{\sqrt {\frac {1}{b}}}$
$v(t)={\sqrt[{k}]{t^{3}}}\quad$
$f(x)={\frac {7}{x^{t}}}\quad$

Antwort

$c^{-({\sqrt {b^{-1}}}-1)}\left(={\frac {1}{c^{{\sqrt {\frac {1}{b}}}-1}}}\right)\quad$
${\frac {3}{k}}\ t^{\frac {3-k}{k}}\left(={\frac {3}{k\ {\sqrt[{k}]{t^{k-3}\ }}}}\right)\quad$
$-7\ t\ x^{t-1}\left(=-{\frac {7\ t}{x^{1-t}}}\right)$

$\$	$\$
	$\ \$
	$\$

Ableitung von Potenzfunktionen schwierig

Berechnen Sie die Ableitung der folgenden Funktionen.

$V(h)={\sqrt[{u}]{\frac {1}{h^{6}}}}$
$H(x)={\sqrt[{3}]{\frac {343}{x^{11}}}}$
$m(n)={\sqrt[{t}]{\frac {5^{t}}{n^{5}}}}$

Antwort

$\ -{\frac {6}{u}}h^{\frac {6-u}{u}}\left(={\frac {6}{u\ {\sqrt[{u}]{h^{6-u}}}}}\right)$
$\ -{\frac {77}{3}}x^{-{\frac {14}{3}}}\left(=-{\frac {77}{3\ {\sqrt[{3}]{x^{14}}}}}\right)\quad$
$-{\frac {5^{2}}{t}}n^{-{\frac {5+t}{t}}}\left(=-{\frac {25}{t\ {\sqrt[{t}]{n^{5+t}}}}}\right)$

$\$	$\$
	$\ \$
	$\$

Ableitung und Grenzwerten

Mit Hilfe von Grenzwerten berechnen Sie die Ableitung

der Funktion $y=ax^{4}$ !

Antwort

Nicht vorhanden

$\$	$\$
	$\$
	$\$

Ableitungen von weiteren Funktionen

Berechnen Sie die Ableitung der folgenden Funktionen.
Berechnen Sie auch den ungefähren Wert der Funktion
und ihrer Ableitung an der Stelle −2.

$\ b(d)=5\ \sin d-\ln d+{\frac {4}{5\ d^{4}}}+6$
$\ v(y)={\frac {7}{\sqrt[{7}]{y^{3}}}}-\cos y+y-y^{-5}$
$\ t(x)=5\ e^{x}-{\sqrt[{3}]{\frac {0{,}125}{x^{6}}}}+\tan x\quad$

Antwort

$\ b'(v)=5\cos d-{\frac {1}{d}}-{\frac {16}{5}}\ d^{-5}$ $\qquad b(-2)=\emptyset \qquad b'(-2)\approx 1{,}48$
$\ v'(y)={-{\frac {3}{4}}}\ y^{-{\frac {10}{7}}}+\sin y+1+5\ t^{-6}\$ $\qquad v(-2)\approx -6{,}75\qquad v'(-2)\approx -0{,}946$
$\ t'(x)=5\ e^{x}+{}\ x^{-3}+{\frac {1}{\cos ^{2}x}}\quad$ $\qquad t(-2)\approx -0{,}621\qquad t'(-2)\approx -0{,}467$

$\$	$\$
	$\ \$
	$\$

Ermittlung einer quadratischen Funktion

Eine quadratische Funktion geht durch die Punkte
$\ P_{1}:(6|2)\$ und $\ P_{2}:(3{,}5|7)$ . Ihre Ableitung
an der Stelle 4 ist null. Wie lautet die Funktion?

Antwort

$Q(x)={\frac {-4\ x^{2}+32\ x-42}{3}}$

$\$	$\$
	$\ \$
	$\$

Ableitungsregeln

Wie lautet die 1. Ableitung der Funktion
$g(a)=\sin {\frac {a^{2}}{3^{a}}}$
(Mit Lösungsschritte!)

Antwort

x\ 3^{-x}(2-\ln 3\ x)\cos(3^{-x}x^{2})

$\$	$\$
	$\ \$
	$\$

Kurvendiskussion

Gegeben ist die Funktion
$g(x)={\tfrac {\sqrt[{3}]{x^{13}}}{5}}-x^{3}+{\tfrac {x^{2}}{5}}-x+1$

Welche sind die lokale Extrempunkte,
die Wendepunkte und die Sattelpunkte
der Funktion?
Welche sind die Nullstellen der Funktion?
Wie viel ist ihre Wert und der Wert ihrer
Ableitung an der Stelle 1,2?
Wie ist ihr Monotonieverhalten?

Antwort

Extrempunkte: $(-1{,}01|2{,}20),\ (0{,}90|0{,}17)$
Sattelpunkte: Keiner
Wendepunkte: $(-0{,}56|1{,}72),\ (0{,}07|0{,}93),\ (0{,}46|0{,}52)$
Nullstellen: $-1{,}56$
$b(1{,}2)=0{,}56\quad b'(1{,}2)=3{,}12$
$]-\infty ;-1{,}01[\ \rightarrow \ steigend,\quad$ $]-1{,}01;0{,}90[\ \rightarrow \ fallend,\quad$ $]-0{,}90;+\infty [\ \rightarrow \ steigend$

$\$	$\$
	$\ \$
	$\$

Kurvendiskussion Umkehraufgaben

Temperatur (°C):	$4$	$5$	$1$
Höhe (dm):	$\ \ 3\ \$	$\ \ 3{,}4\ \$	$\ \ 0\ \$

In einem Diagramm wird die Temperatur in Abhängigkeit von der Höhe in einem kleineren Kühlschrank als quadratische Funktion dargestellt. Aus dem Diagramm werden die Werte in der nebenstehenden Tabelle entnommen.

Erstellen Sie ein Gleichungssystem zur Berechnung der Koeffizienten der Funktion.
Berechnen Sie die Koeffizienten der Funktion.

r'\left({\tfrac {2{\sqrt {3}}+6}{3}}\right)=1.

Wie lautet die Funktion?

Antwort

$\ \left|{\begin{array}{l}\circ \quad 4=a\cdot 3^{2}+b\cdot 3+c\\\circ \quad 1=a\cdot 0^{2}+b\cdot 0+c\\\circ \quad 5=a\cdot 3{,}4^{2}+b\cdot 3{,}4+c\end{array}}\right.\$
$\ a={\tfrac {15}{34}}\quad b=-{\tfrac {11}{34}}\quad c=1\$
$\ r(x)=-{\tfrac {1}{8}}x^{3}+{\tfrac {3}{4}}\ x^{2}\$

$\$	$\$
	$\ \$
	$\$

Binomialverteilung

Die Ansteckungswahrscheinlichkeit eines grippalen Infekts nach einem Kuss am Backen ist 13,5%.

Eine ansteckende Person hat an einem Tag 14 Personen so geküsst. Wie viel ist der Erwartungswert und die Standardabweichung und wie viel die Wahrscheinlichkeit, dass 12 Personen angesteckt wurden? Was ist das wahrscheinlichste Ergebnis?
Eine ansteckende Person hat an einem Tag 9 Personen so geküsst. Wie viel ist der Erwartungswert und die Standardabweichung und wie viel die Wahrscheinlichkeit, dass 5 Personen angesteckt wurden? Was ist das wahrscheinlichste Ergebnis?
Wie viel ist die Wahrscheinlichkeit, dass von 13 geküssten Personen höchstens 4 angesteckt wurden?
Wie viel ist die Wahrscheinlichkeit, dass von 8 geküssten Personen die Hälfte oder mehr angesteckt wurden?

Antwort

$E(x)=1{,}89\quad \sigma \approx 1{,}28\$
$P(X=12)\approx 0\%,$
2 Personen (ca. 29,1%)
$E(x)=1{,}22\quad \sigma \approx 1{,}03\$
$P(X=5)\approx 0{,}32\%,$
1 Person (ca. 38,1%)
$P(X\leq 4)\approx 97{,}75\%$
$P(X\geq 4)\approx 1{,}48\%$

$\$	$\$
	$\ \$
	$\$

Klasse 12

Integral von Potenzfunktionen

Berechnen Sie die Stammfunktionen der folgenden Funktionen.

$i)\ x(y)=y^{7}\quad ii)\ a(c)=(b+1)\ c^{b}\quad iii)\ z(w)={\frac {d}{w}}$

Antwort

$\textstyle \textstyle i)\ {\frac {1}{8}}\ y^{8}+c\qquad ii)\ =c^{b+1}+c\qquad$ $\textstyle iii)\ d\ \ln w+c\qquad$

$\$	$\$
	$\$
	$\$

Integrale von weiteren Funktionen

Berechnen Sie die Stammfunktion der folgenden Funktionen.
Berechnen Sie auch den ungefähren Wert der Funktion
an der Stelle 2,4 und ihrer Stammfunktion zwischen den
Stellen −2,3 und −1

$\ b(t)=2\ \sin t-{\frac {5}{t}}+{\frac {0{,}2}{t^{4}}}+4$
$\ v(b)={\frac {5}{\sqrt[{4}]{b^{3}}}}-\cos b+b-b^{-3}$
$\ t(g)=5\ e^{g}-{\sqrt[{4}]{\frac {625}{g^{5}}}}-\sin g\quad$

Antwort

$\ \int b(t)dt=-{2}\ \cos t-5\ \ln |t|-{\frac {0{,}2}{3v^{3}}}+4\ t+c\ \quad b(2{,}4)\approx 3{,}27\quad \int _{-2{,}3}^{-1}b(v)dv\approx 7{,}01$
$\ \int v(b)db=20\ {\sqrt[{4}]{b}}-\sin b+{\frac {b^{2}}{2}}+{\frac {1}{2\ t^{2}}}+c\ \quad v(2{,}4)\approx 5{,}66\quad \int _{-2{,}3}^{-1}v(b)db\ {\text{undefinierbar}}$
$\ \int t(g)dg=5\ e^{g}-{\frac {20\ }{\ {\sqrt[{4}]{g}}}}+\cos g+c\ \quad t(2{,}4)\approx 52{,}8\quad \int _{-2{,}3}^{-1}t(g)dg\$ undefiniert

$\$	$\$
	$\$
	$\$

Fläche zwischen zwei Funktionen

Berechnen Sie die Fläche zwischen den Funktionen

$\ g(x)=2\log(0{,}5x-2)\$ und $\ f(x)=-0{,}5x^{3}+2\$
und zwischen den Stellen 2 und 3.

Antwort

$\int g(x)dx\$ erst ab 4 definierbar

$\$	$\$
	$\$
	$\$

Normalverteilung

Anwendung der Normalverteilung bei gegebenen Erwartungswert und Standardabweichung

Der

Bluthochdruck ist einer der „vier großen Gesundheitsrisikofaktoren“. Blutdruck ist Normalverteilt und bei gesunden Erwachsenen gilt:

\mu =119{,}2\ mm\,Hg,\ \sigma =7{,}4\ mm\,Hg.\

Laut WHO-Definition hat eine Person Bluthochdruck ab einen Wert von

140\ mm\,Hg.\

Welcher Anteil der gesunden Menschen wäre nach dieser Definition als krank eingestuft?

In welchem symmetrischen Intervall liegen 30% der Fälle?

Füllen Sie die fehlenden Werte in den Kästchen aus!

Welche Eigenschaften hat der Punkt C?

Beschriften Sie die x-Achse!

Zeichnen Sie eine Verteilung mit größerem

\mu

und größerem

\sigma

Veranschaulichen Sie in der Abbildung die Wahrscheinlichkeit, dass der Blutdruck kleiner als 114,8 mmHg ist!

Im nebenstehenden Diagramm ist der Erwartungswert der "spitzeren" Funktion 12,5 und die Standardabweichung 3.

Wie viel ist der Erwartungswert der anderen Funktion?

Die Standardabweichung dieser anderen Funktion ist 4. Beschriften Sie die Stellen, die eine Standardabweichung vom Erwartungswert abweichen!

Antwort

z\approx 0{,}2\%

ca. zwischen 116,3 und 122,1 mmHg

111,8 119,2 bzw. 126,6 mmHg

Wendepunkt (Stelle mit einer

\sigma

Abstand von

\mu

Bei

\mu

119,2 mmHg, jede Einheit

2{,}4{\dot {6}}

m

die ganz flache (blaue) im Vergleich zur lila links

Fläche links von 114,8 schraffieren (fängt ein bisschen links von der Mitte an)

Auch 12,5

Auf der x-Achse, 8 kleine Einheiten links und rechts von

\mu

$\$	$\$
	$\ \$
	$\$

Anwendung der Normalverteilung bei gegebenen Grenzwerten

Der Hämoglobinwert (ähnlich wie Hämatokrit) ist normalverteilt. 20% der Frauen werden von einer Blutspende ausgeschlossen, weil dieser Wert unterhalb von 125 g/l liegt. Wie viel hätte die Standardabweichung sein sollen, wenn der Erwartungswert 133 g/l wäre?

85% der Männer haben einen Wert über 135 g/l und dürfen nach diesem Kriterium Blut spenden. Wie viel soll der Erwartungswert sein, wenn wir annehmen, dass die Standardabweichung 4,7 g/l ist? Zwischen welchen (symmetrischen) Werten liegt dann 95% der Männer?

Antwort

$\sigma \approx 9{,}51\ {\text{g/l}}\quad -/-\quad \mu \approx 139{,}9,\$ ${\text{Grenzen: }}130{,}7-149{,}1\ {\text{g/l}}$

$\$	$\$
	$\$
	$\$

Normalverteilung und Funktionen

Bei einer Normalverteilung hat man festgestellt, dass
Standardabweichung und Erwartungswert voneinander abhängig sind:

\textstyle \sigma ={\mu }^{0{,}4}

.
Wie viel müssen Standardabweichung und Erwartungswert sein,
damit 95 % der Werte oberhalb vom Wert 69 bleibt?

Antwort

$\mu \approx 78{,}4\ \ \sigma \approx 5{,}7$

$\$	$\$
	$\$
	$\$

BILDERVERZEICHNIS

ÖFFNE DEIN HORIZONT!
LERNE MIT MATHEMATRIX!

\quad

\quad

\quad

$\mathbf {MATHE} \mu \alpha T\mathbb {R} ix$
LOGO	CH DE AT

SPENDEN
Der Hauptautor ggf. das Team verdient zwar nicht viel, braucht allerdings dein Geld eigentlich nicht. Wenn du aber doch meinst, dass gute Arbeit belohnt werden soll und dieses Projekt gut findest, kannst du immer in diesem Link spenden. Das ist allerdings vielleicht die einzige Einrichtung mit völliger Transparenz, wo du genau weißt, was mit deinem Geld passiert.

Abgerufen von „https://de.wikibooks.org/w/index.php?title=Mathematrix:_BY_GYM/_Aufgaben_alle/_00&oldid=895199“