Satz vom Minimum und Maximum – Serlo „Mathe für Nicht-Freaks“

Im Folgenden werden wir uns mit stetigen Funktionen auf kompakten Intervallen beschäftigen. Dies sind Intervalle, die abgeschlossen und beschränkt, also von der Form $[a,b]$, sind. Wir werden sehen, dass solche Funktionen immer beschränkt sind und ihr Maximum und Minimum annehmen. Dieser Satz wird Satz vom Minimum und Maximum genannt. Er wird in der Mathematik verwendet, die Existenz von Extrema stetiger Funktionen zu beweisen.

Motivation

Motivation und Intuition hinter dem Satz vom Maximum und Minimum

Nehmen wir eine stetige Funktion $f$, die auf einem kompakten Intervall $[a,b]$ definiert ist. Wir betrachten also eine Funktion $f:[a,b]\to \mathbb {R}$. Diese Funktion besitzt an der Stelle $a$ den Funktionswert $f(a)$ und an der Stelle $b$ den Funktionswert $f(b)$.

Die beiden Funktionswerte f(a) und f(b)

Nun ist $f$ für jede Stelle zwischen $a$ und $b$ definiert. Nun können Graphen stetiger Funktionen, die keine Unterbrechungen im Definitionsbereich besitzen, ohne Absetzen des Stifts gezeichnet werden. Der Graph von $f$ verbindet also die beiden Punkte $(a,f(a))$ und $(b,f(b))$ durch einen durchgehenden Pfad ohne Sprünge. Der folgende Graph zeigt ein Beispiel für eine mögliche Funktion $f$:

Der Graph der Funktion f

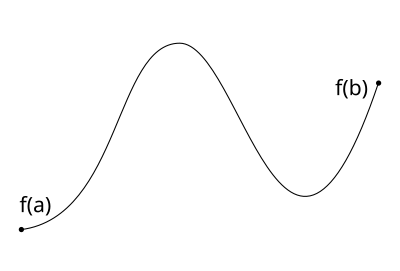
Wir stellen fest, dass im obigen Beispiel die Funktionen $f$ beschränkt ist. Auch nimmt $f$ ihr Maximum und ihr Minimum als Funktionswerte an:

Die Funktion f ist beschränkt und nimmt ihr Maximum und Minimum an

Ist dies immer so? Probiere selbst, die Punkte $(a,f(a))$ und $(b,f(b))$ über einen Graphen zu verbinden, wobei du beim Zeichnen den Stift nicht absetzen darfst. Ist es möglich, so den Graphen einer unbeschränkten Funktion zu zeichnen?

Nein. Egal wie groß oder wie klein die Funktionswerte werden, irgendwann muss man umkehren, um den Endpunkt des Graphen zu erreichen. So bleibt die Funktion beschränkt. In der folgenden Grafik sehen wir, dass der Graph von $f$ zwar sehr große Werte annimmt – jedoch bleibt er beschränkt. Um den Endpunkt zu erreichen, muss man beim Zeichnen des Graphen irgendwann umkehren, wodurch der Graph nicht ins Unendliche wachsen kann:

Eine weitere Funktion mit den Funktionswerten f(a) und f(b), die auch beschränkt ist und die ihr Maximum und Minimum annimmt

Wenn wir die Punkte $(a,f(a))$ und $(b,f(b))$ ohne Absetzen des Stifts miteinander verbinden, dann bleibt nach unserer Überlegung die Funktion beschränkt. Außerdem scheint sie immer ihr Maximum und ihr Minimum anzunehmen. Weil die beiden Randpunkte $a$ und $b$ des Intervalls $[a,b]$ zum Definitionsbereich dazugehören, muss die Funktion dort einen konkreten Wert besitzen. Damit ist die Funktion am Rand „gefangen“ und kann dort nicht gegen Unendlich streben. Die Stetigkeit von $f$ verhindert wiederum ein Streben der Funktion innerhalb des Definitionsbereichs gegen Unendlich, weil der Graph zusammenhängend gezeichnet sein muss. Diese intuitive Erklärung ist natürlich noch weit von einem formalen Beweis entfernt. Für ein erstes Verständnis des Satzes ist sie aber nützlich.

Satz vom Minimum und Maximum

Satz (Satz vom Minimum und Maximum)

Erklärung des Satzes vom Minimum und Maximum. (YouTube-Video vom Kanal Quatematik)

Jede auf einem kompakten Intervall $[a,b]$ definierte stetige Funktion ist beschränkt und nimmt ihr Maximum und Minimum an. Sei also $f:[a,b]\to \mathbb {R}$ mit $a,b\in \mathbb {R}$ und $a<b$ eine stetige Funktion. Es gibt Argumente ${\tilde {x}},{\hat {x}}\in [a,b]$, so dass für alle Argumente $x\in [a,b]$ die Ungleichung $f({\hat {x}})\leq f(x)\leq f({\tilde {x}})$ erfüllt ist.

Beispiel (Satz vom Minimum und Maximum)

Graph der Funktion $f:[0,1]\to \mathbb {R}$ mit $f(x)=x^{2}\cdot \cos(x)\cdot e^{\cos(x)}-\ln(x+1)$. Diese Funktion besitzt ein Maximum und ein Minimum, welche sie auch als Funktionswert annimmt.

Betrachten wir $f:[0,1]\to \mathbb {R}$ mit $f(x)=x^{2}\cdot \cos(x)\cdot e^{\cos(x)}-\ln(x+1)$. Der Definitionsbereich $[0,1]$ ist ein kompaktes Intervall. Außerdem ist $f$ stetig als Komposition der stetigen Funktionen $x\mapsto x^{2}$, $x\mapsto e^{x}$, $x\mapsto \cos(x)$ und $x\mapsto \ln(x+1)$ mit den Definitionsbereichen $[0,1]$. Damit besitzt $f$ ein Maximum und ein Minimum.

Beweis (Satz vom Minimum und Maximum)

Beweis des Satzes vom Maximum und Minimum

Sei $f:[a,b]\to \mathbb {R}$ eine stetige Funktion mit $a,b\in \mathbb {R}$ und $a<b$. Zunächst werden wir beweisen, dass $f$ nach oben beschränkt ist und sein Maximum annimmt. Auf analoge Art und Weise kann die Beschränktheit nach unten und die Annahme des Minimums als Funktionswert gezeigt werden.

Hierzu betrachten wir das Bild $f([a,b])$. Dies ist die Menge aller Funktionswerte, die $f$ annimmt. Nun nehmen wir das Supremum $\sup f([a,b])$ der Menge $f([a,b])$, wobei wir das uneigentliche Supremum $\sup f([a,b])=\infty$ explizit erlauben. Wenn $f$ nach oben unbeschränkt ist, dann ist $\sup f([a,b])=\infty$ und ansonsten ist $\sup([a,b])\in \mathbb {R}$ (weil $f([a,b])\neq \emptyset$ ist, kann der Fall $\sup \emptyset =-\infty$ nicht auftreten).

Nun wissen wir, dass es eine Folge in $f([a,b])$ gibt, die gegen $\sup f([a,b])$ konvergiert (für jede nicht leere Menge $M$ gibt es eine Folge aus $M$, die gegen $\sup M$ konvergiert). Damit gibt es eine Folge $(x_{n})_{n\in \mathbb {N} }$ von Argumenten aus $[a,b]$ mit $\lim _{n\to \infty }f(x_{n})=\sup f([a,b])$.

Nun können wir den Satz von Bolzano-Weierstraß anwenden. Dieser besagt, dass jede Folge aus einem Intervall der Form $[a,b]$ mit $a,b\in \mathbb {R}$ und $a<b$ eine konvergente Teilfolge besitzt. Damit besitzt auch $(x_{n})_{n\in \mathbb {N} }$ eine konvergente Teilfolge $\left(x_{n_{k}}\right)_{k\in \mathbb {N} }$. Sei ${\tilde {x}}$ der Grenzwert der konvergenten Teilfolge $\left(x_{n_{k}}\right)_{k\in \mathbb {N} }$. Wegen $a\leq x_{n_{k}}\leq b$ für alle $k\in \mathbb {N}$ ist auch $a\leq {\tilde {x}}\leq b$ und damit ${\tilde {x}}\in [a,b]$. Also ist ${\tilde {x}}$ ein Argument der Funktion $f$. Weil die Funktion $f$ stetig ist, gilt nach dem Folgenkriterium der Stetigkeit

$f\left({\tilde {x}}\right)=f\left(\lim _{k\to \infty }x_{n_{k}}\right)=\lim _{k\to \infty }f\left(x_{n_{k}}\right)=\sup f([a,b])$

$\sup f([a,b])$ ist ein Funktionswert von $f$ und damit eine reelle Zahl. Dies zeigt, dass $f$ nach oben beschränkt ist. Außerdem haben wir gezeigt, dass $f$ den Wert $\sup f([a,b])$ an der Stelle ${\tilde {x}}$ annimmt. Damit ist $f(x)\leq f({\tilde {x}})$ für alle $x\in [a,b]$ und somit $f({\tilde {x}})$ das Maximum aller Funktionswerte von $f$.

Die Voraussetzungen des Satzes

Voraussetzungen des Satzes vom Maximum und Minimum

Schauen wir uns die Voraussetzungen des Satzes zum Minimum und zum Maximum an. Diese sind

• $f$ ist eine stetige Funktion
• $f$ ist auf einem kompakten Intervall $[a,b]$ definiert

Sind diese Prämissen notwendig oder können sie so abgeschwächt werden, dass der Satz vom Minimum und Maximum trotzdem gilt?

Zur Stetigkeits-Voraussetzung

Funktion $f(x)={\tfrac {1}{x}}$ auf dem Intervall $[-1,1]$ mit $f(0)=0$

Zunächst stellen wir fest, dass die Stetigkeit entscheidend dafür ist, dass $f$ innerhalb des Definitionsbereichs „nicht ausschert“ und gegen $+\infty$ oder $-\infty$ strebt. Wenn wir jede Funktion $f:[a,b]\to \mathbb {R}$ zulassen, finden wir Funktionen, die den Satz vom Maximum und Minimum nicht erfüllen. So ist die folgende Funktion unbeschränkt, welche an der Stelle $x=0$ unstetig ist:

$f:[-1,1]\to \mathbb {R} :x\mapsto {\begin{cases}{\frac {1}{x}}&;x\neq 0\\0&;x=0\end{cases}}$

Die Prämisse, dass $f$ stetig ist, kann also nicht wegfallen.

Zur Intervall-Voraussetzung

Funktion $f(x)={\tfrac {1}{x}}$ auf $(0,1]$

Aber auch die Form des Definitionsbereichs ist wichtig. So müssen wir fordern, dass die Funktion an den Randpunkten des Definitionsbereichs definiert ist (die beiden Randpunkte des Intervalls also zum Definitionsbereich gehören), damit die Funktion dort „eingefangen wird“. Fällt ein Randpunkt aus dem Definitionsbereich weg (wenn wir also halboffene oder offene Intervalle als Definitionsbereich betrachten), dann finden wir Gegenbeispiele. An der offenen Seite des Definitionsbereich kann die Funktion nämlich gegen Unendlich streben. Ein Beispiel hierfür ist die Funktion $g:(0,1]\to \mathbb {R} :x\mapsto {\tfrac {1}{x}}$.

Auch bei einem unbeschränkten Definitionsbereich können Gegenbeispiele gefunden werden. Ein Beispiel hierfür ist die Funktion $h:[0,\infty )\to \mathbb {R} :x\mapsto x^{2}$. Es kann allerdings auch vorkommen, dass eine beschränkte stetige Funktion auf einem beschränkten Definitionsbereich weder Maximum noch Minimum annimmt.

Frage: Besitzt eine stetige und beschränkte Funktion $f$ auf einem beschränkten Definitionsbereich immer ein Maximum und Minimum?

Nein. Ein Beispiel ist die Funktion $f:(0,1)\to \mathbb {R}$, $f(x)=x$. Es gilt: $f((0,1))=(0,1)$. Also besitzt sie weder Maximum, noch Minimum.

Auch Lücken im Definitionsbereich können es einer stetigen Funktion erlauben, „an der Lücke gegen Unendlich zu streben“. Ein Beispiel hierfür ist die stetige und unbeschränkte Funktion $j:[-1,1]\setminus \{0\}\to \mathbb {R} :x\mapsto {\tfrac {1}{x}}$. Weil Null nicht zum Definitionsbereich $[-1,1]\setminus \{0\}=[-1,0)\cup (0,1]$ dazugehört, ist diese Funktion wohldefiniert und stetig. Sie ist aber unbeschränkt und erfüllt somit nicht die Konklusion des Satzes vom Minimum und Maximum.

Ausblick: Verallgemeinerung des Satzes

Doch bedeutet dies, dass für den Satz vom Minimum und Maximum der Definitionsbereich ein Intervall sein muss? Nein. Nimm den Definitionsbereich $D=[a,b]\cup [c,d]$ mit $a<b<c<d$ und eine beliebige auf $D$ definierte stetige und reellwertige Funktion $j$. Wenn wir $j$ auf $[a,b]$ beziehungsweise $[c,d]$ einschränken, dann können wir den Satz vom Minimum und Maximum anwenden. Damit sind sowohl $j_{1}=j|_{[a,b]}$ und $j_{2}=j|_{[c,d]}$ beschränkt und nehmen ihr Maximum und Minimum an. Somit ist aber auch die gesamte Funktion $j$ beschränkt. Ihr Maximum ist der Größere der beiden Maxima von $j_{1}$ und $j_{2}$ und somit nimmt auch $j$ sein Maximum an (analog für das Minimum). Unsere Erkenntnis: Jede stetige Funktion auf dem Definitionsbereich $[a,b]\cup [c,d]$ erfüllt die Konklusion des Satzes vom Minimum und Maximum. Damit ist es möglich, den Satz des Minimums und Maximums auf andere Definitionsbereiche zu verallgemeinern. Später werden wir uns damit beschäftigen, wie es geht.

Im Beweis sehen wir, dass an nur einer Stelle der Definitionsbereich erwähnt wird. Dies ist dort, wo der Satz von Bolzano-Weierstraß verwendet wird. Mit diesem wird gezeigt, dass jede Folge aus dem Definitionsbereich eine konvergente Teilfolge besitzt. Solange also der Satz von Bolzano-Weierstraß für den Definitionsbereich erfüllt ist, kann der Beweis vollzogen werden.

Dies ermöglicht eine Verallgemeinerung des obigen Satzes. Es gibt nämlich mehr reelle Mengen außer Intervalle der Form $[a,b]$, für die der Satz von Bolzano-Weierstraß gilt. Eine solche Menge wird eine folgenkompakte Menge genannt. Die Definition einer folgenkompakten Menge aus den reellen Zahlen ist genau die, dass für sie der Satz von Bolzano-Weierstraß erfüllt ist:

Definition (Folgenkompaktheit)

Eine Teilmenge der reellen Zahlen nennt man genau dann folgenkompakt, wenn jede Folge aus dieser Menge eine konvergente Teilfolge besitzt.

Sobald der Definitionsbereich $D$ einer stetigen Funktion $f:D\to \mathbb {R}$ folgenkompakt ist, muss die Funktion $f$ den Satz vom Minimum und vom Maximum erfüllen. In der Topologie wird Folgenkompaktheit näher untersucht.

Übungsaufgabe: Bild von Polynomen geraden Grades

Übungsaufgabe: Bild von Polynomen geraden Grades

Aufgabe (Bild von Polynomen)

Sei

$p:\mathbb {R} \to \mathbb {R} ,\ p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots +a_{1}x+a_{0}$

eine Polynomfunktion mit $a_{0},a_{1},\ldots ,a_{n-1},a_{n}\in \mathbb {R}$ und $a_{n}\neq 0$. Außerdem sei der Grad von $p$, also $n$, gerade. Zeige: Für den Wertebereich von $p$ gilt

$p(\mathbb {R} )={\begin{cases}[y_{\min },\infty )&{\text{ für }}a_{n}>0,\\(-\infty ,y_{\max }]&{\text{ für }}a_{n}<0.\end{cases}}$

Dabei ist $y_{\min }$ im Fall $a_{n}>0$ und $y_{\max }$ im Fall $a_{n}<0$ eine reelle Zahl.

Beweis (Bild von Polynomen)

Wir beweisen die Aussage für nur für den Fall $a_{n}>0$. Der Fall $a_{n}<0$ kann analog bewiesen werden. Zunächst stellen wir fest, dass das Polynom $p$ als Komposition stetiger Funktionen stetig auf $\mathbb {R}$ ist. Die Vermutung liegt nahe, dass wir den Satz vom Maximum und Minimum verwenden. Jedoch ist $\mathbb {R} =(-\infty ,\infty )$ kein kompaktes Intervall. Deswegen müssen wir den Definitionsbereich geschickt einschränken. Nun gilt $\lim _{x\to \pm \infty }x^{n}=\infty$, da $n$ gerade ist. Daraus folgt:

$\lim _{x\to \pm \infty }p(x)=\lim _{x\to \pm \infty }\underbrace {x^{n}} _{\to \infty }(\underbrace {a_{n}+a_{n-1}x^{-1}+\ldots +a_{1}x^{-n+1}+a_{0}x^{-n}} _{\to a_{n}>0})=\infty$

Nehmen wir ein beliebigen Funktionswert von $p$ – zum Beispiel $p(0)$. Wegen $\lim _{x\to \infty }p(x)=\infty$ gibt es ein $S\in \mathbb {R}$, so dass $p(x)>p(0)$ für alle $x\geq S$ ist. Analog gibt es wegen $\lim _{x\to -\infty }p(x)=\infty$ ein $s\in \mathbb {R}$, so dass $p(x)>p(0)$ für kleineren Argumente $x$ als $s$ ist. Sowohl auf $(-\infty ,s]$ als auch auf $[S,\infty )$ ist das Polynom $p$ größer als der Funktionswert $p(0)$.

Betrachten wir nun das Intervall $[s,S]$. Da das Polynom auf $[S,\infty )$ größer als $p(0)$ ist, kann $0$ kein Element dieser Menge sein und damit ist $S>0$. Analog ist $s<0$. Damit ist $[s,S]$ ein nicht leeres, abgeschlossenes und beschränktes Intervall. Wir können nun den Satz vom Maximum und Minimum anwenden. Das Polynom $p$ besitzt auf $[s,S]$ ein Minimum $y_{\min }$, welches es als Funktionswert annimmt. Nun ist $y_{\min }\leq p(0)$ (wegen $0\in [s,S]$) und damit ist $y_{\min }$ ein globales Minimum des Polynoms.

Aus dem Zwischenwertsatz für stetige Funktion folgt, dass das Bild von $p$ ein Intervall ist (siehe Folgerung aus dem Zwischenwertsatz). Wegen $\lim _{x\to \infty }p(x)=\infty$ und weil $y_{\min }$ ein globales Minimum von $p$ ist, muss das Bild von $p$ von der Form $[y_{\min },\infty )$ sein.

Übungsaufgabe: Stetige Funktion auf [0,1]

Übungsaufgabe: Stetige Funktion auf [0,1]

Aufgabe (Keine stetige Funktion auf kompakten Intervallen nimmt alle ihre Funktionswerte genau zweimal an)

Zeige, dass es keine stetige Funktion $f:[0,1]\to \mathbb {R}$ gibt, die alle ihre Funktionswerte genau zweimal annimmt. Es gibt also keine stetige Funkion $f:[0,1]\to \mathbb {R}$, so dass es für alle $y\in f([0,1])$ genau zwei Zahlen $x_{1},x_{2}\in [0,1]$ mit $f(x_{1})=f(x_{2})=y$ gibt.

Lösung (Keine stetige Funktion auf kompakten Intervallen nimmt alle ihre Funktionswerte genau zweimal an)

Wir führen einen Widerspruchsbeweis. Sei also $f:[0,1]\to \mathbb {R}$ eine stetige Funktion, die alle Ihre Funktionswerte genau zweimal annimmt. Da $f$ stetig und $[0,1]$ ein kompaktes Intervall ist, ist $f$ beschränkt und nimmt sein Maximum $M$ als Funktionswert an. Nach Voraussetzung wird das Maximum auch genau zweimal angenommen. Also gibt es zwei Argumente $x_{M},{\tilde {x}}_{M}\in [0,1]$ mit $f(x_{M})=f({\tilde {x}}_{M})=M$. Sei ohne Beschränkung der Allgemeinheit $x_{M}<{\tilde {x}}_{M}$.

Nun muss $f$ auf den Intervall $[x_{M},{\tilde {x}}_{M}]$ ein Minimum $m$ besitzen. Da $M$ das Maximum von $f$ ist, ist es auch das Maximum von $f|_{[x_{M},{\tilde {x}}_{M}]}$. Es folgt $M\geq m$. Da im Fall $m=M$ die Funktion $f$ auf dem Intervall $[x_{M},{\tilde {x}}_{M}]$ konstant wäre und damit alle Funktionswerte unendlich oft annehmen würde, ist $m<M$.

Da $m$ durch $f$ auf dem Intervall $[x_{M},{\tilde {x}}_{M}]$ angenommen wird und da an den Rändern dieses Intervalls der Funktionswert gleich $M$ ist, gibt es ein $x_{m}$ mit $x_{M}<x_{m}<{\tilde {x}}_{M}$ mit $f(x_{m})=m$. Außerdem wird $m$ an noch einer anderen Stelle ${\tilde {x}}_{m}\in [0,1]$ angenommen. ${\tilde {x}}_{m}$ liegt nun entweder außerhalb des Intervalls $[x_{M},{\tilde {x}}_{M}]$ oder innerhalb.

Fall 1: ${\tilde {x}}_{m}\notin [x_{M},{\tilde {x}}_{M}]$

Nehmen wir den Fall, dass ${\tilde {x}}_{m}$ kein Element von $[x_{M},{\tilde {x}}_{M}]$ ist und betrachten ohne Beschränkung der Allgemeinheit den Fall, dass $x_{M}<x_{m}<{\tilde {x}}_{M}<{\tilde {x}}_{m}$ ist. Betrachten wir den Mittelwert ${\tfrac {M+m}{2}}$ zwischen $M$ und $m$. Dieser Wert wird nach dem Zwischenwertsatz zwischen $x_{M}$ und $x_{m}$ durch die Funktion angenommen, denn es ist $f(x_{M})=M>{\tfrac {M+m}{2}}>m=f(x_{m})$. Analog wird ${\tfrac {M+m}{2}}$ im Bereich $[x_{m},{\tilde {x}}_{M}]$ und im Intervall $[{\tilde {x}}_{M},{\tilde {x}}_{m}]$ angenommen. Damit wird ${\tfrac {M+m}{2}}$ an drei Stellen angenommen, was den Voraussetzungen widerspricht:

Illustration der Funktion f, welche mindestens dreimal den Wert (M+m)/2 annimmt

Fall 2: ${\tilde {x}}_{m}\in [x_{M},{\tilde {x}}_{M}]$

Betrachten wir nun den Fall, dass ${\tilde {x}}_{m}$ innerhalb des Intervalls $[x_{M},{\tilde {x}}_{M}]$ liegt. Nehmen wir ohne Beschränkung der Allgemeinheit an, dass $x_{M}<x_{m}<{\tilde {x}}_{m}<{\tilde {x}}_{M}$ ist. Im Intervall $[x_{m},{\tilde {x}}_{m}]$ nimmt $f$ ein Maximum $M_{2}$ an. Weil $m$ das Minimum auf $[x_{m},{\tilde {x}}_{m}]$ ist, ist $M_{2}\geq m$. Da außerdem $m$ bereits zweimal als Funktionswert angenommen wird, muss $M_{2}>m$ sein. Nun ist $M$ das Maximum von $f$, welches bereits an $x_{M}$ und ${\tilde {x}}_{M}$ angenommen wird und deswegen ist $M>M_{2}>m$.

Nach dem Zwischenwertsatz wird $M_{2}$ wegen $f(x_{M})=M>M_{2}>m=f(x_{m})$ im Intervall $[x_{M},x_{m}]$ angenommen. Außerdem wird wegen $f({\tilde {x}}_{m})=m<M_{2}<M=f({\tilde {x}}_{M})$ ein Argument aus $[{\tilde {x}}_{m},{\tilde {x}}_{M}]$ auf $M_{2}$ abgebildet. Damit wird der Funktionswert $M_{2}$ mindestens dreimal angenommen: Einmal im offenen Intervall $(x_{M},x_{m})$, einmal in $(x_{m},{\tilde {x}}_{m})$ und einmal in $({\tilde {x}}_{m},{\tilde {x}}_{M})$. Dies stellt einen Widerspruch dar:

Illustration der Funktion f, welche mindestens dreimal den Wert M_2 annimmt

Die Aussage der Aufgabe lässt sich im Übrigen noch auf verschiedene Weisen verallgemeinern:

1. Es gibt auf einem allgemeinen kompakten Intervall $[a,b]$ keine stetige Funktion, die jeden ihrer Werte genau zweimal annimmt.
2. Ebenso gibt es keine stetige Funktion $f:\mathbb {R} \to \mathbb {R}$, die jeden ihrer Funktionswerte genau zweimal annimmt.
3. Schließlich kann man zeigen, dass es für jedes $n\in \mathbb {N}$, $n>1$ keine stetige Funktion $f:[a,b]\to \mathbb {R}$ gibt, die jeden ihrer Werte genau $n$ Mal annimmt.

Verständnisaufgabe: Gib jeweils ein Beispiel:

1. Eine stetige Funktion $f:[0,1]\to \mathbb {R}$, die jeden ihrer Funktionswerte genau einmal annimmt.
2. Funktion $f:(0,1]\to \mathbb {R}$, die jeden ihrer Funktionswerte genau zweimal annimmt.

Lösungen:

1. $f:[0,1]\to \mathbb {R}$ mit $f(x)=x$
2. $f:(0,1]\to \mathbb {R}$ mit $f(x)={\begin{cases}2x&0<x\leq {\frac {1}{2}}\\2x-1&{\frac {1}{2}}<x\leq 1\end{cases}}$