Linearkombinationen – Serlo „Mathe für Nicht-Freaks“
Über Linearkombinationen können Vektoren zerlegt oder aus anderen Vektoren dargestellt werden. In diesem Kapitel werden wir das Konzept der Linearkombinationen kennen lernen.
Motivation des Begriffs der Linearkombination
BearbeitenVerbindungen auf einer Karte
BearbeitenSehen wir uns die folgende Karte an:
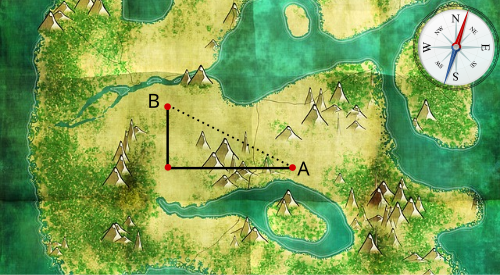
Unser Ziel ist, es von unserem Startpunkt aus zum Endpunkt zu gelangen. Selbstverständlich gibt es dabei unendlich viele Möglichkeiten. Wollen wir auf dem kürzesten Weg von nach gelangen, so gehen wir auf der Verbindungsgeraden der beiden Punkte entlang. Eine andere Möglichkeit ist, vom Startpunkt drei Schritte nach Westen zu gehen bis wir auf Höhe vom Endpunkt angekommen sind, um anschließend zwei Schritte nach Norden in Richtung zu gehen.
Wenn der Standardvektor Richtung Westen und der Standardvektor Richtung Norden ist, so kann über folgende gewichtete Summe von und dargestellt werden:
Kräftezerlegung
BearbeitenWir wollen uns im Folgenden ein Beispiel aus der Physik ansehen. Dazu betrachten wir den in der Abbildung zu sehenden Ball auf der als reibungsfrei angenommenen schiefen Ebene. Wir nehmen dabei im Folgenden an, dass der Ball sich selbst überlassen wird.
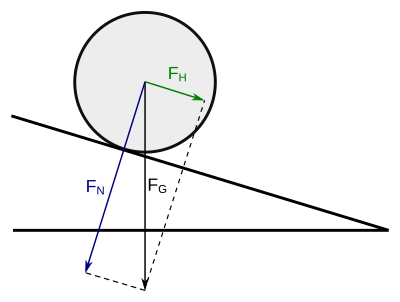
Auf unseren betrachteten Ball wirkt die Gravitationskraft senkrecht zur Horizontalen. Der Ball kann durch die schiefe Ebene nun aber nicht einfach nach unten fallen, da die Bewegungsrichtung durch die Rampe vorgegeben ist. Aus diesem Grund müssen wir die Gewichtskraft zerlegen. Die Zerlegung erfolgt in einen Anteil senkrecht zur schiefen Ebene. Diesen Anteil bezeichnen wir als die Normalkomponente der Gewichtskraft . Des Weiteren existiert ein Anteil parallel zur schiefen Ebene, die Hangabtriebskraft , welche den Ball beschleunigt. Insgesamt gilt also für auf den Ball wirkenden Kräfte der Zusammenhang:
Die Gewichtskraft ist damit eine einfach gewichtete Summe von zwei Teilkräften.
Zerlegung eines Vektors in der Ebene
BearbeitenBetrachten wir einen beliebigen Vektor mit in der Ebene. Jeden solchen Vektor können wir dann darstellen als
Dies zeigt, dass wir jeden Vektor des als gewichtete Summe der beiden Standardvektoren , auffassen können.
Definition der Linearkombination
BearbeitenWir haben gesehen, dass wir in vielen Beispielen Vektoren als eine Summe von anderen Vektoren mit Vorfaktoren darstellen können. Wir wollen unsere Beobachtung verallgemeinern und diese Summen in Zukunft Linearkombinationen nennen:
Definition (Linearkombination)
Sei ein -Vektorraum und ein beliebiger Körper. Jede Summe der Form mit und heißt Linearkombination. Lässt sich ein Vektor schreiben als , so sagen wir, dass der Vektor eine Linearkombination der Vektoren mit den Koeffizienten ist.
Beispiele
BearbeitenBeispiel (Linearkombination)
Der Vektor lässt sich schreiben als
Mit anderen Worten ist der Vektor eine Linearkombination der Vektoren , und mit den Koeffizienten , und .
Beispiel (Schwerpunktsberechnung)
Betrachten wir nun noch ein weiteres typisches Beispiel aus der Physik. Die Abbildung zeigt drei Teilchen im mit den Massen , und , die durch die jeweiligen Ortsvektoren , und beschrieben werden können:

Die Gesamtmasse setzt sich zusammen aus der Summe der Einzelmassen der betrachteten Teilchen, also . Dann lässt sich der Schwerpunktsvektor des Systems aus den drei Masseteilchen bestimmen zu:
Auch hier sehen wir wieder unsere nun wohlbekannte Struktur, dass der Schwerpunktsvektor eine gewichtete Summe der einzelnen Ortsvektoren , , und damit eine Linearkombination dieser Vektoren ist.
Gleichungssystem als Linearkombination
BearbeitenWir betrachten das beliebig gewählte folgende Gleichungssystem
Mit Hilfe dieser Schreibweise wird ersichtlich, dass die Lösung eines Gleichungssystems im Grunde lediglich in der Aufgabe besteht, die entsprechenden unbekannten Koeffizienten einer Linearkombination zu bestimmen.
Linearkombination als Standardform
BearbeitenWir wollen aufzeigen, dass wir die Linearkombination als eine Art Standardform für beliebige Verknüpfungen von Vektoren auffassen können. Beliebige Hintereinanderausführungen von Operationen wie Streckungen und Addition der Vektoren lassen sich als Linearkombination aufgreifen. Dafür betrachten wir exemplarisch zwei beliebige Vektoren und sowie die Skalare , , und . Nehmen wir folgende Verknüpfung von und :
Durch schrittweise Anwendung der Vektorraumaxiome können wir obige Verknüpfung in eine Linearkombination umformen:
Am Ende der Umformung erhalten wir eine Linearkombination der Vektoren und . Dabei haben wir jeweils angemerkt, welche Vektorraumaxiome bei den jeweiligen Schritten verwendet wurde. Anhand dieses Beispiels lässt sich leicht erahnen, dass sich dieses Vorgehen für sämtliche Verknüpfungen von Vektoren anwenden lässt. Damit ist die Linearkombination eine Art Standardform für beliebige Verknüpfungen von Vektoren.









![{\displaystyle {\begin{aligned}{\vec {F_{G}}}&={\vec {F_{H}}}+{\vec {F_{N}}}\\[0.3em]&=1\cdot {\vec {F_{H}}}+1\cdot {\vec {F_{N}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1903670f4771124bd1567382cbf57b052c2de6f)












































![{\displaystyle {\begin{aligned}&{\mathcal {\beta }}(\alpha (v+\mu w)+\lambda v)\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Vektorielles Distributivgesetz }}\right.}\\[0.3em]=&\beta (\alpha v+\alpha (\mu w))+\lambda v)\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Assoziativgesetz für Skalare }}\right.}\\[0.3em]=&\beta (\alpha v+(\alpha \mu )w)+\lambda v)\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Vektorielles Distributivgesetz }}\right.}\\[0.3em]=&\beta (\alpha v)+\beta (\alpha \mu )w+\beta (\lambda v)\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Assoziativgesetz für Skalare }}\right.}\\[0.3em]=&(\beta \alpha )v+(\beta \alpha \mu )w+(\beta \lambda )v\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{Kommutativgesetz }}\right.}\\[0.3em]=&(\beta \alpha )v+(\beta \lambda )v+(\beta \alpha \mu )w\\[0.3em]&\quad {\color {OliveGreen}\left\downarrow \ {\text{skalares Distributivgesetz }}\right.}\\[0.3em]=&(\beta \alpha +\beta \lambda )v+\beta \alpha \mu w\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ce20f2c9ad41d6994e526319fa4ed39b4918e92)