Bestimmte Divergenz, uneigentliche Konvergenz – Serlo „Mathe für Nicht-Freaks“
Bisher haben wir vor allem die Konvergenz von Folgen untersucht. In diesem Kapitel werden wir uns mit divergenten Folgen beschäftigen. Hier können nämlich zwei Arten der Divergenz unterschieden werden: Bestimmte und unbestimmte Divergenz.
Motivation
BearbeitenWenn wir uns divergente Folgen anschauen, dann gibt es Folgen wie , und , die ein eindeutiges Streben gegen oder aufweisen:
-
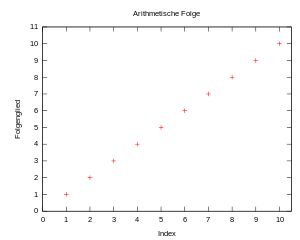
Die Folge strebt eindeutig gegen .
-
Die Folge strebt eindeutig gegen .
-
Die Folge strebt eindeutig gegen .
Bei solchen Folgen werden wir sagen, dass sie bestimmt gegen beziehungsweise gegen divergieren. Demgegenüber gibt es bei Folgen wie oder kein solches eindeutiges Streben. Die Folge ist beschränkt und kann deswegen weder gegen noch gegen divergieren.
Die Folge ist zwar unbeschränkt, ihr Streben ist aber nicht eindeutig. Diese Folge besitzt nämlich Teilfolgen, die gegen streben, und andere Teilfolgen, die gegen streben:
-
Die alternierende Folge ist beschränkt und kann deswegen nicht gegen unendlich streben.
-
Die Folge ist zwar unbeschränkt, besitzt aber auch kein eindeutiges Streben gegen oder .
Definition
BearbeitenWir haben gesehen, dass die bestimmte Divergenz das eindeutige Streben einer Folgen gegen oder gegen ist. Wie kann dies mathematisch formuliert werden?
Beginnen wir mit der bestimmten Divergenz gegen : Wenn eine Folge gegen strebt, dann wird diese Folge größer als jede Zahl – egal wie groß sie ist. Mehr noch: Egal wie groß man eine Zahl annimmt, fast alle Folgenglieder dieser Folge liegen über dieser Zahl. Es existiert also ein Index , ab dem alle folgenden Folgenglieder größer gleich sind. Damit wird die Zahl ab dem Index nicht mehr unterschritten. Dies ist dann auch die Definition der bestimmten Divergenz gegen :
Definition (Bestimmte Divergenz gegen )
Eine Folge divergiert bestimmt gegen , wenn für jede Zahl fast alle Folgenglieder größer oder gleich sind. Für alle reellen Zahlen gibt es also einen Index , sodass für alle ist:
Wir können die Aussageform der bestimmten Divergenz gegen unendlich so übersetzen:
Analog können wir die bestimmte Divergenz gegen definieren:
Definition (Bestimmte Divergenz gegen )
Eine Folge divergiert bestimmt gegen , wenn für jede Zahl fast alle Folgenglieder kleiner oder gleich sind. Für alle reellen Zahlen gibt es also einen Index , sodass für alle ist:
Schreibweise
BearbeitenWenn eine Folge gegen bestimmt divergiert, dann schreiben wir
Analog benutzen wir folgende Schreibweise, wenn eine Folge gegen bestimmt divergiert:
Beispiele
BearbeitenBeispiel
Beispiel (Geometrische Folge)
Wie wir im Kapitel „unbeschränkte Folgen divergieren“ schon gesehen haben, divergiert die geometrische Folge für . In diesem Kapitel haben wir gezeigt, dass für und für jede relle Zahl die Ungleichung für fast alle erfüllt ist. Also ist für . Ist hingegen , so liegt keine bestimmte Divergenz vor. Für gerade ist dann nämlich positiv und für ungerade ist es negativ. Damit kann die geometrische Folge für nicht bestimmt divergieren.
Bestimmte Divergenz als uneigentliche Konvergenz
BearbeitenDie Schreibweise suggeriert, dass die Folge gegen unendlich konvergiert. Hier liegt aber eine Divergenz und keine Konvergenz vor! Das Symbol ist nämlich keine reelle Zahl. Konvergente Folgen dürfen per Definition aber nur reelle Zahlen als Grenzwerte besitzen. Es gibt allerdings Parallelen zwischen der Konvergenz und der bestimmten Divergenz:
| Konvergenz | Bestimmte Divergenz |
|---|---|
| In jeder -Umgebung liegen fast alle Folgenglieder. | In jedem Intervall liegen fast alle Folgenglieder. |
| Alle Teilfolgen konvergieren gegen denselben Grenzwert. | Auch alle Teilfolgen divergieren bestimmt gegen . |
| Jede konvergente Folge ist beschränkt. | Jede bestimmt divergente Folge ist unbeschränkt. |
Dementsprechend gibt es für bestimmte Divergenz auch den Begriff der uneigentlichen Konvergenz. Das Wort „uneigentliche Konvergenz“ deutet darauf hin, dass die bestimmte Divergenz gewisse Ähnlichkeiten zur Konvergenz aufweist. Sie ist aber in ihrem Wesen eine Divergenz.
Warnung
Es ist wichtig, dass wir uns merken, dass die bestimmte Divergenz eine Art der Divergenz ist, obwohl sie der Konvergenz ähnelt und wir sie als uneigentliche Konvergenz bezeichnen. Wir dürfen also auf bestimmt divergente Folgen keine Rechenregeln anwenden, die nur für konvergente Folgen gelten. Ein Beispiel ist die Produktregel . Diese Regel gilt für bestimmt divergente Folgen nicht, wie die folgende Umformung zeigt:
Man erhält also die falsche Aussage , wenn man die Produktregel auf bestimmt divergente Folgen anwendet. Wir müssen also vorsichtig sein, welche Rechenregeln wir auf bestimmt divergente Folgen anwenden.


















![{\displaystyle {\begin{array}{l}\underbrace {{\underset {}{}}\forall S\in \mathbb {R} } _{{\text{Für jede reelle Zahl }}S}\ \underbrace {{\underset {}{}}\exists N\in \mathbb {N} } _{{\text{ existiert ein Mindestindex }}N,}\ \underbrace {{\underset {}{}}\forall n\geq N:} _{{\text{sodass für alle Indizes }}n\geq N}\\[0.5em]\quad \quad \underbrace {{\underset {}{}}a_{n}\geq S} _{{\text{ das Folgenglied }}a_{n}{\text{ größer gleich }}S{\text{ ist}}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2281f0a489495d78f3f8dfd839c5b9bde3ffe7a6)






![{\displaystyle {\begin{aligned}\lim _{n\to \infty }n&=+\infty \\[0.5em]\lim _{n\to \infty }n^{2}&=+\infty \\[0.5em]\lim _{n\to \infty }-n&=-\infty \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2436811277a75f6bc9f9458093cb79a8be1241d9)














