Go/ Grundbegriffe/ Augen

Formal gesprochen sind Augen freie Gitterpunkte, die vollständig von Steinen der gleichen Farbe umschlossen sind. Als solche sind sie die wohl wichtigste Form im Go. Thematisch eng verbunden sind die Begriffe "Leben und Tod", da die Bewertung einer Augenform in den meisten Fällen die Frage "Lebt die Gruppe oder ist sie tot?" betrifft. Die Einordnung in ein eigenes Kapitel erfolgt aus Übersichtsgründen.

Gruppen mit einem Auge

• 
  Dia 1
• 
  Dia 2
• 
  Dia 3

Ein Beispiel für eine schwarze Gruppe mit einem Auge zeigt Dia 1. Das Auge ist dabei durch ein Kreuz markiert. Die Frage ist nun, ob diese Gruppe nun von Weiß gefangen werden kann, oder nicht. Direkt in das Auge darf Weiß zunächst nicht setzen, da dies ein Selbstmord wäre.

Die Situation ändert sich aber, wenn Weiß die äußeren Freiheiten der schwarzen Gruppe komplett besetzt hat (Dia 2). Die schwarze Gruppe hat dann nur noch die eine Freiheit im Auge. Weiß kann nun in das Auge setzen, da nun alle Freiheiten der schwarzen Gruppe genommen sind und die Steine entfernt werden dürfen (Dia 3).

• 
  Dia 4
• 
  Dia 5
• 
  Dia 6

Wie sieht nun die Situation aus, wenn das Auge mehrere Gitterpunkte umfasst? Ein entsprechendes Beispiel zeigt Dia 4. Weiß kann in das Auge setzen, so dass Dia 5 entsteht. Schwarz hat danach nur noch eine Freiheit, kann den weißen Stein im Auge schlagen. Es entsteht eine schwarze Gruppe, die wieder nur eine Freiheit besitzt, so dass sie beim nächsten Zug von Weiß geschlagen werden kann (Dia 6).

Fazit: Gruppen mit nur einem Auge können gefangen werden, wenn es nicht gelingt aus dem einen Auge zwei zu bilden.

Gruppen mit zwei Augen

• 
  Dia 1
• 
  Dia 2
• 
  Dia 3

Dia 1 zeigt nun eine schwarze Gruppe mit zwei Augen. Diese Gruppe kann nicht von Weiß geschlagen werden, da sie durch die beiden Augen zwei Freiheiten besitzt, die nicht gleichzeitig von Weiß besetzt werden können. Allgemein gilt, dass Gruppen, die zwei Augen besitzen nicht mehr geschlagen werden können.

Somit gehört es zu den entscheidenden Zielen beim Go Steingruppen mit mindestens zwei Augen zu bauen. Dia 2+3 zeigen zwei weitere Beispiele für lebende Gruppen mit zwei Augen in der Ecke. Mit nur sechs Steinen gehören diese Gruppen zu den kleinsten lebenden Gruppen, die überhaupt möglich sind.

Unechte Augen

Unechtes Auge

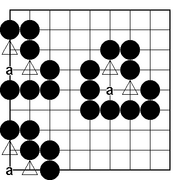
Neben den echten Augen wie in den Beispielen oben, gibt es auch noch sog. unechte Augen. Ein Beispiel für eine Gruppe mit einem unechten Auge zeigt das rechte Bild. Das Bild sieht Dia 3 oben auf den ersten Blick sehr ähnlich. Allerdings, handelt es sich bei dem Auge auf a nicht um ein echtes Auge.

Wenn Weiß auf a setzt, kann die schwarze Dreiergruppe gefangen werden. Gruppen mit falschen Augen sind daran zu erkennen, dass die am falschen Auge beteilige Teilgruppe nur Freiheiten in dem falschen Auge hat, aber keine Freiheiten in dem zweiten Auge. Da diese Teilgruppe nur Freiheiten in einem der beiden Augen hat, kann sie gefangen werden.

[Anmerkung: Eine andere Unterscheidung zwischen echten und unechten Augen, ist weniger anschaulich.
Vereinfacht: um ein "echtes" Auge zu erhalten müssen mindestens drei der vier diagonal benachbarten Felder von schwarz besetzt sein.
Kompliziert: Dies gilt nicht am Rand und in den Ecken. Ausserdem gibt es einige Ausnahmen, die mit nur zwei besetzten Diagonalfeldern auskommen, dabei muss aber zumindest das dritte Diagonalfeld wiederum in einem "echten" Auge liegen.]

Allerdings bergen unechte Augen durchaus Gefahren für den Angreifer. Wenn er sich in Sicherheit wiegt und das unechte Auge nicht attackiert, kann der Verteidiger in vielen anderen Fällen verbinden und hat dann ein echtes Auge.

Augenpunkte

Oft ist es schwierig zu erkennen, ob aus einer Gruppe mit nur einem Auge eine Gruppe mit zwei Augen gebildet werden kann oder nicht. Deshalb sollte man die typischen Grundformen erkennen. Prinzipiell gibt es eine große Anzahl möglicher Konstellationen (Robert Jasiek spricht von "wenigen hundert"). Die Auswahl hier beschränkt sich auf die häufig namentlich erwähnten und betrachtet vornehmlich die Gitterpunkte innerhalb des Auge. Ein solches Auge kann zwei, drei, vier und auch mehr Punkte umfassen.

Bei den nun folgenden Beispielen, wurde jeweils davon ausgegangen, dass alle äußeren Freiheiten der Gruppen vom Gegner besetzt sind. Um die Übersichtlichkeit zu verbessern, wurden die weißen Steine aber nicht immer in die Diagramme eingezeichnet.

Ein Auge mit zwei Punkten

• 
  Dia 1
• 
  Dia 2

Augen, die nur zwei Gitterpunkte umschließen, sind immer tot (Dia 1). Nicht zu verwechseln ist diese Situation mit den in Dia 2 gezeigten Konstellationen. Hier sind die Gitterpunkte bereits Gebiet, da es sich um jeweils zwei Augen handelt.

Ein Auge mit drei Punkten

• 
  Dia 1
• 
  Dia 2

Für drei zusammenhängende Gitterpunkte, die umschlossen sind, gibt es prinzipiell nur zwei verschiedene Möglichkeiten.

Die erste Möglichkeit besteht darin, dass die drei Gitterpunkte in einer Reihe liegen. Beispiele für die sogenannte Gestreckte Drei zeigen die Gruppen in Dia 1. Diese Gruppen leben nur dann, wenn Schwarz am Zug ist und auf die mit a gekennzeichneten Punkte in der Mitte setzt, so dass jeweils Gruppen mit zwei Augen gebildet werden. Ist Weiß am Zug und setzt auf a so ist die schwarze Gruppe tot. Die Punkte a sind somit überlebenswichtige für die Gestreckten Drei und heißen deshalb vitale Punkte.

Die andere Möglichkeit für ein Auge mit drei Gitterpunkten ist die Gebogene Drei. Beispiele für die Gebogenen Drei zeigt Dia 2. Auch diese Gruppen leben nur, wenn Schwarz am Zug ist und auf die mit a gekennzeichneten Gitterpunkte setzt. Ist Weiß am Zug sind die Gruppen tot.

Ein Auge mit vier Punkten

Für ein Auge mit vier Punkten gibt es insgesamt fünf verschiedene Anordnungen:

• Gestreckte Vier
• Gebogene Vier
• Verschobene Vier
• Quadrat
• Vierer-Pyramide

Gestreckte Vier

Gebogene Vier

Gebogene Vier in der Ecke

Die Gestreckte Vier und die Gebogene Vier (wenn sie nicht in der Ecke liegt), leben unabhängig davon, ob Weiß oder Schwarz am Zug ist, da diese Gruppen zwei vitale Punkte (a+b) besitzen. Man sagt a und b sind Miai (jap. 見合い). Spielt Weiß auf a, spielt Schwarz auf b und vice versa.

Eine Besonderheit gilt, wenn die Gebogene Vier in der Ecke liegt (mit dem "Knick" als Eckpunkt). Diese Stellung ist unsicher, da die schwarze Form nur einen vitalen Punkt a hat. Ist Schwarz am Zug, kann er ihn besetzen und die Gruppe lebt mit zwei Augen.

Der Gitterpunkt b ist in dem Sinne nicht vital, dass Schwarz mit ihm nur leben kann, wenn Weiß nicht vorher auf a gespielt hat. Sprachlich korrekt müsste man sagen, dass die Gebogene Vier in der Ecke zwei vitale Punkte hat, die nicht Miai sind und daher ein "Tötungspunkt" existiert.

Ist Weiß am Zug verhindert sein Stein auf dem vitalen Punkt ein bedingungsloses Leben von Schwarz. Genauer gesagt ist die Bedingung in dieser Situtation der Ausgang des entstehenden Ko-Kampfes.

Dia 1

Dia 2

Dia 3

Nach Weiß 3 in Dia 2 darf Schwarz wegen der Ko-Regel nicht sofort zurückschlagen. Hat Schwarz keine hinreichend große Ko-Drohung oder ignoriert Weiß sie einfach, kann er die schwarze Gruppe töten (Dia 3).

Dia 4

Dia 5

Dia 6

Dia 7

Daran ändert sich auch nichts, wenn Schwarz eine zusätzliche Freiheit außen hat (Dia 4). Hier muss Weiß nur aufpassen, die richtige Fortsetzung zu wählen. Spielt er auf a in Dia 5 entsteht ein neues Ko, spielt er auf b lebt Schwarz bedingungslos in der Ecke. Richtig ist der Zug in Dia 6, der in einer toten Gebogenen Drei endet (Dia 7).

Erst mit zwei oder mehr Außenfreiheiten kann die gebogene Vier in der Ecke leben. Die in manchen Go-Büchern erwähnte Formulierung, dass die gebogene Vier in der Ecke immer tot ist, bezieht sich auf eine spezielle Spielsituation, die an dieser Stelle nicht ausgeführt wird.

• 
  Verschobene Vier
• 
  Quadrat
• 
  Vierer-Pyramide

Die Verschobene Vier hat zwei vitale Punkte und lebt somit unabhängig davon, wer gerade am Zug ist. Die Einschränkung dieser Aussage, wenn diese Form in der Ecke liegt, bleibt an dieser Stelle unbehandelt.

Das Quadrat ist immer tot, unabhängig davon wer gerade am Zug ist. Man sollte es also vermeiden eine Gruppe mit einem Quadrat zu bilden.

Die Vierer-Pyramide hat einen vitalen Punkt und lebt somit nur bedingt. Ist Schwarz am Zug so lebt diese Gruppe. Ist Weiß am Zug und setzt auf a, so ist die Gruppe tot.

Ein Auge mit fünf Punkten

• 
  Kreuz Fünf
• 
  Sperrige Fünf

Augen der Größe fünf haben alle zwei vitale Punkte außer der Kreuz Fünf und der Sperrigen Fünf. Beide Formen haben nur einen vitalen Punkt a. Somit leben sie nur, wenn der Besitzer am Zug ist.

Bei der Kreuz Fünf erkennt man unmittelbar, dass nachdem Weiß den vitalen Punkt in der Mitte besetzt hat, keine zwei Augen gebildet werden können.

• 
  Dia 3
• 
  Dia 4
• 
  Dia 5

Etwas komplizierter ist die Situation bei der Sperrigen Fünf. Was passiert, nachdem Weiß auf den vitalen Punkt gesetzt hat? Für Schwarz gibt es nun die drei Möglichkeiten a, b oder c.

Schwarz 2 in Dia 4 sollte mit Weiß 3 beantwortet werden. Wenn dies nicht geschieht, kann, wie im Dia 5 zu sehen ist, Schwarz 4 zwei Augen bilden, was ein großer Fehler von Weiß wäre.

Ein Auge mit sechs Punkten

Rechteckige Sechs in der Ecke

Blumensechs

Augen, die sechs Gitterpunkte umschließen, leben alle bedingungslos, außer der Rechteckigen Sechs in der Ecke und der Blumensechs.

Ein Auge mit sieben oder mehr Punkten

Augen mit sieben oder mehr Gitterpunkten leben immer bedingungslos. Das beste Ergebnis für einen Angreifer ist ein Seki, wenn der Verteidiger einmal tenuki spielt, bei der sogenannten Schmetterlings-Sieben.

Arme und reiche Augen

Die Unterscheidung zwischen armen und reichen Augen betrifft ihre Qualität in Fangwettläufen und hängt nur indirekt mit den umschlossenen Gitterpunkten zusammen. Die Einordnung in dieses Kapitel erfolgt aus Gründen der Übersicht. Thematisch gehört dieses Unterkapitel nicht unmittelbar zum Rest.

Bei armen Augen entspricht die Anzahl der Augenfreiheiten den vorhandenen freien Gitterpunkten. Dazu zählen Augen, die drei oder weniger Punkte umschließen.

Bei einem oder zwei Gitterpunkten ist dies unmittelbar anschaulich (Dia 1-4).

Dia 1

Dia 2

Dia 3

Dia 4

Dia 5

Dia 6

Dia 7

Bei drei Gitterpunkten kann man bei der Beurteilung einen Denkfehler begehen. Aus Sicht des Angreifers entspricht die Anzahl von gegnerischen Freiheiten der Anzahl von Zügen, die er benötigt, um die Steine zu fangen (Dia 5-7).

Auf den ersten Blick benötigt Weiß vier Züge. Richtig ist, dass er vier Steine setzen muss, wenn Schwarz antwortet. Aber Weiß benötigt effektiv lediglich drei Züge, da Schwarz entweder selbst einmal im Auge spielt (Dia 6) und sich damit Weiß 2 und Schwarz 3 gegenseitig aufheben. Oder er läßt Weiß mit dem dritten Zug auf Schwarz 3 spielen.

Bei reichen Augen ist die Anzahl der Augenfreiheiten größer als die Anzahl der umschlossenen Gitterpunkte. Gleichzeitig gehören in Fangwettläufen die vorhandenen geteilten Freiheiten dem reicheren Auge (unabhängig von den in einer konkreten Spielsitutation vorhandenen Augenfreiheiten), da der angreifende Spieler mehrere "Durchläufe" benötigt, um es aufzufüllen.

Dia 8

Dia 9

Dia 10

Dia 11

Wie die Sequenz in Dia 8-11 zeigt, benötigt Weiß effektiv 5 Züge, um die schwarze Gruppe zu fangen. Weiß 3 und Schwarz 4, sowie Weiß 6 und Schwarz 7 heben sich gegenseitig auf.

Dia 12

Dia 13

Ein Auge, das 5 Gitterpunkte umschließt (Dia 12), hat insgesamt 8 Augenfreiheiten.

Nach Schwarz 5 in Dia 13 wurde aus dem 5er-Auge das 4er-Auge von oben, das 5 Augenfreiheiten hat. Dafür benötigte Weiß effektiv 3 Züge (Weiß 4 und Schwarz 5 heben sich wieder auf).

Die allgemeine Berechnung ist eine einfache Folge mit der Formel

$AF(AP)=\textstyle {\frac {AP^{2}-3AP}{2}}+3{\text{, für }}AP>2$

Allerdings hat diese Formel eher theoretischen Wert, da im Spiel eigentlich nur Augen bis Größe 6 relevant sind.

Daher merkt man sich einfach nur:

• 3er Auge hat 3 Freiheiten
• 4er Auge hat 5 Freiheiten
• 5er Auge hat 8 Freiheiten
• 6er Auge hat 12 Freiheiten

Eine abschließende Bemerkung. Bei Augenformen, die einen vitalen Punkt haben, kann ein Semeai verhindert werden. Daher ist die tatsächliche Anzahl der Augenfreiheiten dieser Augenformen im Spiel selbst immer um mindestens eins reduziert, da innerhalb des Auges schon ein gegnerischer Stein sitzen muss.

Entsprechend sind bei zwei vitalen Punkten mindestens zwei Freiheiten bereits belegt.

Reiche Augen in der Ecke

Reiche Augen können in der Ecke einen Teil ihrer Freiheiten verlieren und unter Umständen arm werden.

Dia 1

Dia 2

Dia 3

Das 4er-Auge in Dia 1 hat nicht 5, sondern, wie die Sequenz in Dia 2 zeigt, nur 3 Freiheiten. Will Schwarz dies verhindern, verschlimmert er die Situtation nur, da er sich selbst eine Freiheit nimmt (Dia 3).

Hier muss Schwarz ein weißes Auge verhindern und damit hat das 5er-Auge statt normal sieben (8-1) Freiheiten nur noch drei.

Hier ist kein weißes Auge möglich und Schwarz hat die normalen sieben (8-1) Freiheiten.

Eine erschöpfende Illustration aller Fälle, in denen reiche Augen in der Ecke weniger Freiheiten besitzen oder gar arm werden, würde ein Buch füllen.

Für die allgemeine Bewertung läßt sich sagen, dass ein reiches Auge einen Teil seiner Freiheiten verliert, wenn der Besitzer selbst im Auge spielen muss, um ein gegnerisches Auge zu verhindern.

Damit ist aber nicht automatisch gesagt, dass es seine Qualität als reiches Auge in einem Fangwettlauf verliert. Dies ist nur der Fall, wenn das gegnerische Auge nicht verhindert werden kann, wie in Dia 1. Dieses 4er-Auge ist arm.

Dia 4

Das schwarze 5er-Auge hat nur 3 Freiheiten, aber es ist immer noch reich und damit zählt die markierte geteilte Freiheit für Schwarz. Weiß ist tot.