Vektoren und Vektorräume in der Schule – Serlo „Mathe für Nicht-Freaks“

Vektoren werden in der Schulmathematik als Elemente der Ebene oder des Raumes aufgefasst. Die Hochschulmathematik abstrahiert diesen Begriff und fasst Vektoren allgemeiner auf. In diesem Kapitel wiederholen wir, was Vektoren in der Schulmathematik auszeichnet.

Vektorielle Größen in den Naturwissenschaften

Größen, die durch Länge und Richtung im Raum definiert sind, nennt man auch Vektoren. Sie sind in den Naturwissenschaften essentiell, insbesondere in der Physik und in technischen Disziplinen.

So unterscheidet man in den Naturwissenschaftenzwischen skalaren und vektoriellen Größen. Skalare Größen sind durch ihren reellen Zahlenwert und ihre zugehörige Einheit bestimmt. So beschreibt die Angabe ${\color {OliveGreen}2}\,{\color {Blue}\mathrm {kg} }$, welche aus dem Zahlenwert ${\color {OliveGreen}2}$ und der Einheit ${\color {Blue}\mathrm {kg} }$ besteht, eine Masse eindeutig. Zwei Gegenstände, deren Masse gleich $2\,\mathrm {kg}$ ist, haben dieselbe Masse. Beispiele skalarer Größen in der Physik sind Temperatur, Druck, Energie, Dichte, Arbeit.

Größen, die durch einen Betrag und eine Richtung gegeben sind, heißen vektorielle Größen bzw. Vektoren. Sie werden nicht durch einen Zahlenwert und der Einheit allein beschrieben. Eine vektorielle Größe benötigt noch die Angabe der Richtung, in die sie wirkt. Zwei Vektoren sind nur gleich, wenn neben dem Betrag dieser Größe (angegeben durch Zahlenwert und Einheit) auch deren Richtungen identisch sind. Beispiele vektorieller Größen in der Physik sind Geschwindigkeit, Beschleunigung, Kraft, Drehmoment, Drehimpuls.

Eine Kraft von $5\,\mathrm {N}$ ist noch nicht vollständig bestimmt, solange wir nicht ihre Wirkungsrichtung kennen. Angenommen, zwei Kräfte von $5\,\mathrm {N}$ werden auf ein Objekt ausgeübt. Die erste nennen wir ${\vec {K}}_{1}$ und wirkt senkrecht nach unten. Die andere hingegen wirkt senkrecht nach oben und heißt ${\vec {K}}_{2}$. Dann ist ${\vec {K}}_{2}=-{\vec {K}}_{1}$ und beide Kräfte stimmen nicht überein, obwohl sie den gleichen Betrag haben. Die Addition der Kräfte führt zu der resultierenden Kraft von $0\,\mathrm {N}$. Zur Beschreibung solcher Größen werden Vektoren benötigt.

Wir werden später sehen, dass Vektoren mathematisch viel allgemeiner definiert werden. Auch andere Objekte, wie Abbildungen, Folgen und vieles mehr können als Vektoren aufgefasst werden.

Vektoren in der Geometrie

Wir wollen nun kurz die Nutzung der Vektoren in der Geometrie, so wie sie dir aus der Schule bekannt sind, wiederholen.

Stelle dir zwei unterschiedliche Punkte $A$ und $B$ in der Ebene vor. Wir zeichnen nun einen Pfeil von $A$ nach $B$ und schreiben dafür ${\overrightarrow {AB}}$ und bezeichnen diesen Pfeil als Vektorpfeil.

Hinweis

Diesen Vektor findet man in der Literatur auch oft nur als Buchstabe beschrieben, also statt ${\overrightarrow {AB}}$ wird zum Beispiel ${\vec {a}}$ geschrieben.

Der Pfeil ist vollständig bestimmt durch seine Länge und seine Richtung, die durch die Angabe (der Pfeil führt von $A$ nach $B$) eindeutig festgelegt ist. Die Pfeillänge eines Vektors entspricht dabei seinem Betrag, während die Pfeilspitze in die Richtung des Vektors weist.

Ein Vektor von Startpunkt A nach Endpunkt B und seine Länge

Hinweis

Alle Vektorpfeile ${\overrightarrow {XY}}$, die zu ${\overrightarrow {AB}}$ parallel sind und die gleiche Länge haben, nennen wir parallelgleich. Für parallelgleiche Vektorpfeile schreiben wir ${\overrightarrow {AB}}={\overrightarrow {XY}}$. Die Menge aller parallelgleichen Vektorpfeile bezeichnen wir als Vektor und jeder Vektorpfeil dieser Menge heißt Repräsentant des Vektors. Der Einfachheit halber nennen wir einen Repräsentanten ${\overrightarrow {AB}}$ der Menge Vektor selbst einen Vektor.

Ein ähnliches Vorgehen mit Repräsentanten gibt es bei Brüchen:

${\tfrac {3}{5}};\,{\tfrac {18}{30}};\,{\tfrac {51}{85}};\,{\tfrac {-6}{-10}}\cdots$ sind Repräsentanten des Bruchs mit dem Wert $0,6$. Auch hier nennen wir die Repräsentanten der Einfachheit halber selbst Bruch.

Wir können zusammenfassend folgendes definieren:

Definition (gleiche, parallele und inverse Vektoren)

Die Vektoren ${\vec {a}}$ und ${\vec {b}}$ heißen parallelgleich, wenn sie in Richtung und Länge übereinstimmen.

Zwei Vektoren ${\vec {a}}$ und ${\vec {b}}$ mit gleicher Richtung (Orientierung) heißen zueinander parallel.

Zwei Vektoren mit entgegengesetzter Richtung (Orientierung) nennt man antiparallel.

Der zu einem Vektor ${\vec {a}}$ gehörende Vektor ${\vec {-a}}$ heißt inverser Vektor oder Gegenvektor und besitzt die gleiche Länge wie der Vektor ${\vec {a}}$, ist jedoch antiparallel.

Gegenvektoren oder inverse Vektoren

Zusammenfassend können wir also sagen, Vektoren in der Ebene sind Objekte (Pfeile), die eine Parallelverschiebung in der Ebene beschreiben. Der zugehörige Vektorraum wird als $\mathbb {R} ^{2}$ bezeichnet. In der Geometrie werden die Vektoren durch einen Pfeil dargestellt. Wir können einen Vektor durch einen Buchstaben mit Pfeil notieren, wie z. B. ${\vec {v}}$. Ein Pfeil hat immer eine Länge und eine Richtung. Algebraisch wird die Richtung durch einen Spaltenvektor mit zwei Komponenten angegeben, ${\vec {r}}={\begin{pmatrix}r_{1}\\r_{2}\end{pmatrix}}$.

Was bedeutet dieses? Wir betrachten einen Punkt $P$ in einem rechtwinkeligen kartesischen Koordinatensystem. Der Punkt in dieser Ebene wird beschrieben durch einen sogenannten Ortsvektor, der vom Nullpunkt ${\vec {0}}={\begin{pmatrix}0\\0\end{pmatrix}}$ zum Punkt $P$ geht. Dabei wird der Punkt angegeben durch seine Entfernung $p_{1}$ vom Nullpunkt auf der $x_{1}$-Achse und seine Entfernung $p_{2}$ vom Nullpunkt auf der $x_{2}$-Achse. Wir schreiben dann $P={\begin{pmatrix}p_{1}\\p_{2}\end{pmatrix}}$. Um den Punkt $P$ ins Koordinatensystem einzuzeichnen, gehen wir also vom Nullpunkt des Koordinatensystems zunächst $p_{1}$ Längeneinheiten auf der $x_{1}$-Achse nach rechts (und erreichen auf der $x_{1}$-Achse den Punkt $P_{x_{1}}$ mit den Koordinaten ${\begin{pmatrix}p_{1}\\0\end{pmatrix}}$ und von dort $p_{2}$ Längeneinheiten senkrecht nach oben (also parallel zur $x_{2}$-Achse). Dieser Endpunkt ist dann der Punkt $P$ und hat die Koordinaten ${\begin{pmatrix}p_{1}\\p_{2}\end{pmatrix}}$.

To-Do:

• Bild dazu noch anfertigen

Damit wir die Länge des Ortsvektors ${\vec {OP}}={\vec {p}}$ bestimmen können, betrachten wir das rechtwinkelige Dreieck $OP_{x_{1}}P$. Der Ortsvektor ${\vec {OP}}={\vec {p}}$ ist die Hypotenuse dieses rechtwinkeligen Dreiecks und hat die Länge $p$. Nach dem Satz des Pythagoras gilt:

$p^{2}={p_{1}}^{2}+{p_{2}}^{2}$

Also ist die Länge des Ortsvektors

$|{\vec {p}}|={\sqrt {{p_{1}}^{2}+{p_{2}}^{2}}}$

Da wir an der (positiven) Länge des Ortsvektors interessiert sind, benötigen wir nur den Betrag der Wurzel, also die positive Wurzel.

To-Do:

• Bildnotation an den Text anpassen

Ein Vektor von Startpunkt A nach Endpunkt B und seine Länge

Addition von Vektorpfeilen

Die Vektoren ${\vec {a}}$ und ${\vec {b}}$ werden zur Addition durch Pfeile mit einem gemeinsamen Anfangspunkt dargestellt und zu einem Parallelogramm ergänzt. Der diagonale Pfeil ${\vec {c}}$ vom gemeinsamen Anfangspunkt zur gegenüberliegenden Ecke stellt dann die Summe der beiden Vektoren dar. In der Physik verwendet man diese Konstruktion beim Kräfteparallelogramm.

In der Mathematik wird die Addition von Vektorpfeilen ${\vec {a}}+{\vec {b}}={\vec {c}}$ auch so erklärt: Zunächst wird der Pfeil ${\vec {a}}$ gezeichnet. An die Pfeilspitze wird er zu ${\vec {b}}$ parallele Pfeil ${\vec {b'}}$ abgetragen. Der Vektorpfeil, der vom Ursprungspunkt des Vektorpfeils ${\vec {a}}$ zum Endpunkt des Vektorpfeils ${\vec {b'}}$ führt ist der Vektorpfeil ${\vec {c}}={\vec {a}}+{\vec {b}}$. Bei dieser Beschreibung wird berücksichtigt, dass der zum Vektor ${\vec {b}}$ parallele, gleich lange Vektor ${\vec {b'}}$ den selben Vektor darstellt. Also ${\vec {b}}={\vec {b'}}$. Damit ist obige Addition eindeutig definiert.

Wir können die Vektoren auch in ihrer Koordinatenschreibweise darstellen, nämlich als ${\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}$ und ${\vec {b}}={\begin{pmatrix}b_{1}\\b_{2}\end{pmatrix}}$. Dann bedeutet obiges Vorgehen, wir verlängern die Koordinate $a_{1}$ um die Koordinate $b_{1}$ und erhalten $c_{1}=a_{1}+b_{1}$. Ebenso verlängern wir die Koordinate $a_{2}$ um die Koordinate $b_{2}$ und erhalten $c_{2}=a_{2}+b_{2}$. Bei der Addition addieren wir also einfach die Koordinaten und erhalten so die Koordinaten des Vektors der Summe ${\vec {a}}+{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}+{\begin{pmatrix}b_{1}\\b_{2}\end{pmatrix}}={\begin{pmatrix}{a_{1}+b_{1}}\\{a_{2}+b_{2}}\end{pmatrix}}={\vec {c}}$. Auch hier wird wieder berücksichtigt, dass parallele gleichlange Vektorpfeile den selben Vektor darstellen.

Addition von Vektorpfeilen

Skalare Multiplikation

Die zweite Operation, die skalare Multiplikation eines Vektors mit einer reellen Zahl (einem Skalar), ist dir sicher auch aus der Schule bekannt. Sie bedeutet die Streckung, die Verkürzung oder die Umorientierung der Vektorpfeile.

Betrachten wir einen Vektor ${\vec {w}}={\begin{pmatrix}w_{1}\\w_{2}\end{pmatrix}}$. Die Länge von ${\vec {w}}$ ist $|{\vec {w}}|={\sqrt {{w_{1}}^{2}+{w_{2}}^{2}}}$. Verdoppeln wir nun die Länge dieses Vektors, so erhalten wir $|2\cdot {\vec {w}}|=2\cdot {\sqrt {{w_{1}}^{2}+{w_{2}}^{2}}}={\sqrt {4\cdot ({{w_{1}}^{2}+{w_{2}}^{2}})}}={\sqrt {4\cdot {w_{1}}^{2}+4\cdot {w_{2}}^{2}}}={\sqrt {(2\cdot w_{1})^{2}+(2\cdot w_{2})^{2}}}$. Das bedeutet aber für die doppelte Länge müssen wir sowohl die $w_{1}-$Komponente als auch die $w_{2}-$Komponente verdoppeln. Damit gilt: $2\cdot {\vec {w}}=2\cdot {\begin{pmatrix}w_{1}\\w_{2}\end{pmatrix}}={\begin{pmatrix}{2\cdot w_{1}}\\{2\cdot w_{2}}\end{pmatrix}}$.

Damit wird ein Vektor verdoppelt, indem wir zweimal die Länge des Vektors in dieselbe Richtung gehen. Man sagt auch der Vektor wird um den Faktor 2 gestreckt. Allgemein wird der Vektor ${\vec {v}}$ um den Faktor $k>1$ gestreckt, wenn ${\vec {w}}=k\cdot {\vec {v}}$ gilt.

Wählt man $k<1$, dann wird der Vektor um diesen Faktor gekürzt. Wenn z.B. der Vektor ${\vec {v}}$ halbiert wird, dann gilt ${\vec {w}}={\tfrac {1}{2}}\cdot {\vec {v}}$. Diese Operation nennt mann dann Verkürzung oder Stauchung des Vektors. Allgemein wird die Multiplikation eines Vektors mit einer reellen Zahl eine skalare Multiplikation genannt. Ist die reelle Zahl, mit der der Vektor multipliziert wird, negativ, dreht sich die Richtung des Vektors um.

Skalarmultiplikation: der Vektor w wird mit der Zahl 2 multipliziert und der Vektor v mit der Zahl -1

Wenn wir einen Vektor in entgegengesetzter Richtung zurückgehen, gelangen wir wieder an den Ausgangspunkt des Vektors. Das heißt ${\vec {v}}+(-1)\cdot {\vec {v}}={\begin{pmatrix}v_{1}\\v_{2}\end{pmatrix}}+{\begin{pmatrix}-v_{1}\\-v_{2}\end{pmatrix}}={\begin{pmatrix}v_{1}+{-v_{1}}\\v_{2}+{-v_{2}}\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}$. Obwohl dieses Ergebnis kein Vektor ist, wird er als Nullvektor erklärt, dies ist ein Vektor ohne Länge. Man benötigt ihn, damit die Vektoren bzgl. der Addition eine Gruppe sind.

Alles oben Gesagte gilt analog auch für den euklidischen Raum $\mathbb {R} ^{3}$.

Vektoren im dreidimensionalen Raum

Wenden wir uns Vektoren im dreidimensionalem Raum $\mathbb {R} ^{3}$ zu. Ein solcher Vektor ${\vec {a}}\in \mathbb {R} ^{3}$ kann durch Angabe seiner drei Komponenten beschrieben werden:

${\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}$

So ist der folgende Vektor ${\vec {r}}$ durch die Angabe der drei Koordinaten $x_{p}$, $y_{p}$ und $z_{p}$ eindeutig definiert:

Dreidimensionaler Vektor, welcher im Koordinatensystem über die Angabe von drei Koordinaten eindeutig definiert ist

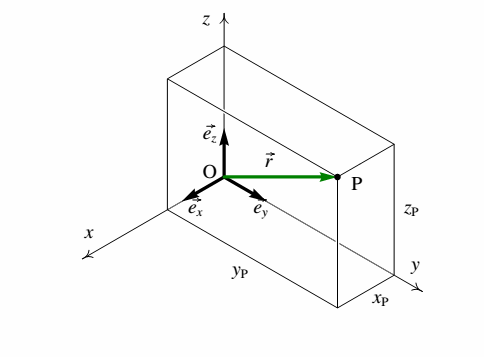
Addition im $\mathbb {R} ^{3}$

Die Addition und die skalare Multiplikation (wie Streckungen und Stauchungen) im $R^{3}$ funktionieren analog wie in der Ebene $\mathbb {R} ^{2}$. Zwei Vektoren ${\vec {a}}$ und ${\vec {b}}$ aus dem $\mathbb {R} ^{3}$ werden addiert, indem man ihre Komponenten addiert:

${\vec {a}}+{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}+{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}{a_{1}+b_{1}}\\{a_{2}+b_{2}}\\{a_{3}+b_{3}}\end{pmatrix}}$

Auch die Subtraktion wird komponentenweise durchgeführt:

${\vec {a}}-{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}-{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}-b_{1}\\a_{2}-b_{2}\\a_{3}-b_{3}\end{pmatrix}}$

Skalare Multiplikation

Ein Vektor ${\vec {a}}\in \mathbb {R} ^{3}$ wird mit einem Skalierungsfaktor $s\in \mathbb {R}$ multipliziert, indem jede Komponente des Vektors mit $s$ multipliziert wird:

$s\cdot {\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}={\begin{pmatrix}sa_{1}\\sa_{2}\\sa_{3}\end{pmatrix}}$

Der Vektor $s\cdot {\vec {a}}$ ist $|s|$-mal so lang wie der Vektor ${\vec {a}}$. Dies bedeutet konkret:

• Für $|s|<1$ wird der Vektor verkleinert.
• Für $|s|>1$ wird der Vektor vergrößert.
• Für $s>0$ hat $s\cdot {\vec {a}}$ die gleiche Richtung wie ${\vec {a}}$.
• Für $s<0$ hat $s\cdot {\vec {a}}$ die Gegenrichtung von ${\vec {a}}$.

Im Besonderen ist $1{\vec {a}}={\vec {a}}$ und $(-1){\vec {a}}=-{\vec {a}}$.

Kollineare Vektoren

Zwei Vektoren, von denen einer ein Vielfaches des anderen ist, sind parallel und man nennt sie kollineare Vektoren. So sind die Vektoren ${\vec {a}}=(1,3,5)^{T}$ und ${\vec {b}}=(3,9,15)^{T}$ kollinear, denn ${\vec {b}}=3{\vec {a}}$.