Folge – Serlo „Mathe für Nicht-Freaks“

Die Folge ist einer der wichtigsten Begriffe in der Analysis. Anhand von Folgen werden wir nämlich später den Begriff des Grenzwerts definieren. Damit wiederum können wir alle wichtigen Konzepte der Analysis wie die Ableitung und die Stetigkeit einführen.

Der Begriff der Folge im Alltag

Einführung von Folgen anhand von einfachen Beispielen. (YouTube-Video vom Kanal Quatematik)

Der Begriff der „Folge“ ist uns bereits aus dem alltäglichen Leben bekannt:

Frage: Welche Beispiele für eine Folge kennst du?

Im Alltag gibt es einige Beispiele von Folgen, welche oftmals als „Abfolge“ oder „Reihenfolge“ bezeichnet werden. Denk an die Reihenfolge der Sachen, die du nach dem Aufstehen machst: 1. Zähneputzen, 2. Duschen, 3. Anziehen, 4. Kaffee kochen, 5. Kaffee trinken, …

Denk auch an die vielen Folgen, die im Laufe der Zeit verlängert werden. Ein Beispiel ist die Folge der Nationen, die die Fußballweltmeisterschaft gewonnen haben (sowohl bei den Männern als auch bei den Frauen): 1. Uruguay, 2. Italien, 3. Italien, 4. Uruguay, 6. Deutschland, …

Allen Beispielen ist gemeinsam, dass die Reihenfolge der Elemente einer Folge genau festgelegt ist. Es gibt eine genau definierte Anordnung der Folgenglieder, die beachtet werden muss. Nach dem Aufstehen sollte man zuerst Kaffee kochen, bevor man diesen trinkt (die umgekehrte Reihenfolge wäre suboptimal  ).

Außerdem können in einer Folge ein oder mehrere Objekte mehrmals als Folgenglieder auftreten. In der Folge der Fußballweltmeister kommen einige Nationen mehr als einmal vor, weil sie die Fußballweltmeisterschaft mehr als einmal gewonnen haben. Dies unterscheidet eine Folge insbesondere von einer Menge. Für eine Menge kann nämlich nicht sinnvoll gefragt werden, wie oft ein Element in ihr vorkommt. Man kann nur fragen, ob ein Objekt Element einer Menge ist oder nicht.

Des Weiteren kannst du die einzelnen Folgenglieder einer Folge durchnummerieren. Du kannst sagen, wer der erste Präsident der USA, der zweite und so weiter war. Jedem Element einer Folge kann also eine oder mehrere Zahlen zugeordnet werden, die angeben, wo dieses Objekt in der Folge vorkommt.

Viele der im Alltag bekannten Folgen sind endlich, es sind aber auch unendliche Folgen vorstellbar. Würde man bis in alle Ewigkeit Fußballweltmeisterschaften austragen, wäre die Folge der Fußballweltmeister unendlich lang.

Formale Definition

Kommen wir nun zu dem Begriff der Folge in der Mathematik. Der große Unterschied zum Folgenbegriff im Alltag ist der, dass in der Mathematik eine Folge immer unendlich lang ist. In der Mathematik gibt es auch endliche Folgen, welche aber „Tupel“ genannt werden. Diese sind endliche Abfolgen von Objekten und entsprechen den endlichen Folgen aus dem Alltag.

Eine Folge ist also eine unendliche Abfolge $(a_{1},a_{2},a_{3},a_{4},\ldots )$ von Objekten. Dabei steht $a_{1}$ für das Objekt an der ersten Stelle, $a_{2}$ für das Objekt an der zweiten Stelle und so weiter. Für Folgen gibt es die abkürzende Schreibweise $(a_{n})_{n\in \mathbb {N} }$. Damit lautet die (intuitive) Definition einer Folge:

Eine Folge $(a_{n})_{n\in \mathbb {N} }$ ist eine unendliche Abfolge von Objekten:

$(a_{n})_{n\in \mathbb {N} }=(a_{1},a_{2},a_{3},a_{4},\ldots )$

Diese Definition ist intuitiv, weil wir den Begriff „unendliche Abfolge“ nicht exakt definiert haben. Dies muss für eine exakte Definition nachgeholt werden.

Beispiel (Folge)

Die Folge $(a_{n})_{n\in \mathbb {N} }$ der natürlichen Zahlen ist:

$(a_{n})_{n\in \mathbb {N} }=(1,\,2,\,3,\,4,\,5,\ldots )$

Die Folge $(b_{n})_{n\in \mathbb {N} }$ der Zweierpotenzen ist:

$(b_{n})_{n\in \mathbb {N} }=(1,\,2,\,4,\,8,\,16,\ldots )$

Verständnisaufgabe: Schreibe diese Folgen in der gerade kennengelernten Folgenschreibweise!

1. Folge der Quadratzahlen
2. Folge der positiven ungeraden Zahlen

1. $(a_{n})_{n\in \mathbb {N} }=(1,\,4,\,9,\,16,\,25,\ldots )$
2. $(b_{n})_{n\in \mathbb {N} }=(1,\,3,\,5,\,7,\,9,\ldots )$

Wichtige Begriffe

Die einzelnen Elemente $a_{n}$ einer Folge werden Folgenglieder genannt. Dabei werden die Folgenglieder mit einer natürlichen Zahl $n$ durchnummeriert. Diese natürliche Zahl nennt man Index. So ist beispielsweise $a_{4}$ das Folgenglied zum Index $4$.

Für eine Folge mit Elementen aus der Menge $M$ ist ein Folgenglied ein konkretes Element aus der Menge $M$. Nehmen wir die Folge $(1,\ 1,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ldots )$. Das Folgenglied $a_{1}$ ist das identische Objekt wie $a_{2}$ oder $a_{3}$, nämlich die Zahl $1$.

Meint man die gesamte Folge, schreibt man $\left(a_{n}\right)_{n\in \mathbb {N} }$. Zwei Kurzschreibweisen für $\left(a_{n}\right)_{n\in \mathbb {N} }$ sind $(a_{n})_{n}$ und $(a_{n})$. Häufig wird der Buchstabe $n$ als Indexvariable genutzt. Jeder Buchstabe kann aber als Indexvariable verwendet werden, solange er im jeweiligen Kontext keine andere Bedeutung hat. So sind auch die Schreibweisen $\left(a_{i}\right)_{i\in \mathbb {N} }$ oder $\left(a_{k}\right)_{k\in \mathbb {N} }$ möglich.

In der Analysis 1 betrachten wir vor allem Folgen mit reellen Zahlen als Folgenglieder. Diese speziellen Folgen nennt man reelle Folgen. In folgender Übersicht und in folgender Tabelle sind alle wesentlichen Begriffe zu den Bestandteilen von Folgen zusammengefasst:

$(a_{n})_{n\in \mathbb {N} }=\overbrace {(a_{1},\,{\color {OliveGreen}\underbrace {a_{2}} _{\text{Folgenglied}}},\,a_{3},\,a_{\color {Blue}\underbrace {{}_{4}} _{\text{Index}}},\,\ldots )} ^{\text{Folge}}$

Begriff	Schreibweise	Definition
Folge	$(a_{n})_{n\in \mathbb {N} }$ oder kurz $(a_{n})$	Eine Folge ist eine unendliche Abfolge von Objekten.
Folgenglied	$a_{n}$	Ein Folgenglied ist ein konkretes Objekt, das in der Folge an einer bestimmten Stelle vorkommt.
Index	$n$	Der Index ist eine natürliche Zahl, die die Folgenglieder durchnummeriert.

Warnung

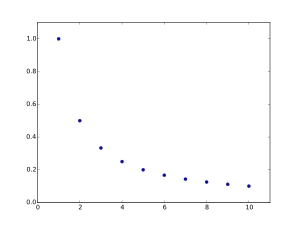
Einige Studenten stellen sich unter einer reellen Folge eine kontinuierliche Funktion vor (insbesondere, wenn sie diese zeichnen wollen). Dies ist jedoch falsch, da eine reelle Folge nur aus einer Abfolge einzelner reeller Zahlen besteht. Dies demonstriert die folgende Gegenüberstellung der harmonischen Folge $(a_{n})_{n\in \mathbb {N} }=\left({\tfrac {1}{n}}\right)_{n\in \mathbb {N} }=\left({\tfrac {1}{1}},{\tfrac {1}{2}},{\tfrac {1}{3}},\ldots \right)$ mit der Funktion $f:\mathbb {R} ^{+}\rightarrow \mathbb {R} ^{+}$ mit $f(x)={\tfrac {1}{x}}$. Beachte, dass es bei der harmonischen Folge im Gegensatz zur Funktion $f(x)={\tfrac {1}{x}}$ nur diskrete Werte (einzelne Punkte) im Graphen gibt:

• 
  Die harmonische Folge, definiert durch $a_{n}={\frac {1}{n}}$, hat nur diskrete Werte.
• 
  Zum Vergleich: Die Funktion $f(x)={\tfrac {1}{x}}$ mit dem Definitionsbereich der positiven reellen Zahlen.

Definition als Funktion

Definition

Oben haben wir die Folge intuitiv als unendliche Abfolge von Objekten definiert. Mit Hilfe des Funktionenbegriffs kann diese Definition konkretisiert und vor allem mathematisch exakt formuliert werden. Hierzu nehmen wir die Menge der natürlichen Zahlen und ordnen jeder natürlichen Zahl $n$ ein beliebiges Objekt $a_{n}$ zu (wobei diese Objekte aus einer Menge $M$ stammen, in der wir eine Folge bilden möchten). Damit erhalten wir eine unendliche und durchnummerierte Abfolge beliebiger Objekte, wie die folgende Skizze verdeutlicht:

${\begin{array}{ccccl}1&2&3&4&\ldots \\\downarrow &\downarrow &\downarrow &\downarrow &\\a_{1}&a_{2}&a_{3}&a_{4}&\ldots \end{array}}$

Eine solche Zuordnung ist nichts anderes als eine Funktion $\mathbb {N} \rightarrow M$, also eine Abbildung von den natürlichen Zahlen in eine Menge $M$, die alle möglichen Folgenglieder enthält. So haben wir bei der Folge der deutschen Bundeskanzler die Zuordnung:

${\begin{array}{cccccl}1&2&3&4&5&\ldots \\\downarrow &\downarrow &\downarrow &\downarrow &\downarrow &\\{\text{Adenauer}}&{\text{Erhard}}&{\text{Kiesinger}}&{\text{Brandt}}&{\text{Schmidt}}&\ldots \\\end{array}}$

Die „unendliche Abfolge“ von Folgengliedern können wir somit als eine Funktion auffassen, die für jede natürliche Zahl $n$ angibt, was das $n$-te Folgenglied sein soll:

Definition (Folge)

Eine Folge in einer Menge $M$ ist eine Abbildung

$f:\mathbb {N} \to M:n\mapsto f(n)=:a_{n}$

Wir schreiben $(a_{n})_{n\in \mathbb {N} }$ anstelle von $f$.

Obige Definition nutzt nur bereits bekannte Konzepte und erfüllt damit die Anforderungen an eine mathematisch exakte Definition. Deswegen wird sie in den meisten Lehrbüchern als Definition einer Folge verwendet.

Anmerkungen

Bei einer Folge $(a_{n})_{n\in \mathbb {N} }$ mit Folgengliedern aus der Menge $M$ steht die Kurzschreibweise $(a_{n})_{n\in \mathbb {N} }=(a_{1},a_{2},\ldots )$ also für eine Funktion $f:\mathbb {N} \to M,n\mapsto a_{n}$. Folgen sind also nichts anderes als Funktionen.

Nehmen wir die beiden Folgen $(a_{n})_{n\in \mathbb {N} }=(f:\mathbb {N} \to \mathbb {N} ,n\mapsto n)$ und $(b_{n})_{n\in \mathbb {N} }=(g:\mathbb {N} \to \mathbb {R} ,n\mapsto n)$. Streng genommen, sind beide Folgen verschieden, da die Zielmenge einmal $\mathbb {N}$ und einmal $\mathbb {R}$ ist und damit die Funktionen nicht gleich sind. Ihre Kurzschreibweisen unterscheiden sich aber nicht: $(a_{n})_{n\in \mathbb {N} }=(1,\ 2,\ 3,\ 4,\ldots )$ und $(b_{n})_{n\in \mathbb {N} }=(1,\ 2,\ 3,\ 4,\ldots )$. Diese Unterscheidung wird deutlich, wenn man $(a_{n})_{n\in \mathbb {N} }$ als Folge in den natürlichen Zahlen und $(b_{n})_{n\in \mathbb {N} }$ als Folge in den reellen Zahlen bezeichnet.

Um anzudeuten, dass eine Folge $(a_{n})_{n\in \mathbb {N} }$ eine Abbildung von den natürlichen Zahlen in die Menge $M$ ist, sagt man, dass $(a_{n})_{n\in \mathbb {N} }$ eine Folge in $M$ ist. Manchmal wird auch die Schreibweise $(a_{n})_{n\in \mathbb {N} }\subseteq M$ benutzt.

Verständnisfrage: Warum haben wir eine Folge $(a_{n})_{n\in \mathbb {N} }$ nicht als die Menge $\{a_{n}|n\in \mathbb {N} \}=\{a_{1},a_{2},a_{3},\ldots \}$ definiert? Was ist der Unterschied?

Dafür gibt es vor allem zwei Gründe. Wir erläutern beide anhand des Beispiels der Folge der Fußball-Weltmeister seit 1990 (wir gehen hier davon aus, dass in Zukunft jedes vierte Jahr eine Fußballweltmeisterschaft stattfindet, es also unendlich viele Fußballweltmeisterschaften gibt):

$(a_{n})_{n\in \mathbb {N} }=({\text{Deutschland, Brasilien, Frankreich, Brasilien, Italien, Spanien, Deutschland, }}\ldots )$

Die Abbildung $f:\mathbb {N} \to \{{\text{Länder}}\}$ ist hier also definiert durch

${\begin{aligned}&f(1):={\text{Deutschland}}\ ,\ f(2)={\text{Brasilien}}\ ,\ f(3):={\text{Frankreich}}\ ,\\&f(4):={\text{Brasilien}}\ ,\ f(5):={\text{Italien}}\ ,\ f(6):={\text{Spanien}}\ ,\\&f(7):={\text{Deutschland}}\ ,\ldots \end{aligned}}$

1. In einer Folge kann ein Element mehrmals vorkommen, in einer Menge nicht. Brasilien ist mehrmals Fußballweltmeister, Frankreich (zumindest bisher) nicht. Betrachtet man die Folge $(a_{n})_{n\in \mathbb {N} }$, kann man dies ablesen. Kennt man nur die Menge der Fußballweltmeister $\{a_{n}|n\in \mathbb {N} \}=\{{\text{Deutschland, Brasilien, Frankreich, }}\ldots \}$, kann man nicht herausfinden, ob Brasilien mehrfacher Fußballweltmeister ist.
2. In einer Folge gibt es eine Reihenfolge der Elemente. Die Objekte einer Menge haben keine Reihenfolge. An der Folge $(a_{n})_{n\in \mathbb {N} }$ können wir ablesen, welches Land die dritte Fußballweltmeisterschaft seit 1990 gewonnen hat: $a_{3}=f(3)={\text{Frankreich}}$. Kennen wir nur die Menge der Fußballweltmeister $\{{\text{Deutschland, Brasilien, Frankreich, }}\ldots \}=\{{\text{Frankreich, Deutschland, Brasilien, }}\ldots \}$, wissen wir nicht, welches Land die dritte Fußballweltmeisterschaft nach 1990 gewonnen hat.

Arten von Folgen

Eine Intervallschachtelung ist eine Folge von Mengen.

Die ersten Folgenglieder einer Folge von quadratischen Funktionen.

Folgen können beliebige Objekte als Folgenglieder besitzen. So sind reelle Folgen Folgen von reellen Zahlen. Dies ist auch der Typ der meisten Folgen, die uns in der Analysis begegnen werden. Es ist aber auch möglich, Folgen von komplexen Zahlen zu haben, welche komplexe Folgen genannt werden. Aber auch Folgen von Mengen oder Folgen von Funktionen sind möglich.

In den letzten Kapiteln haben wir bereits Intervallschachtelungen kennengelernt. Da Intervalle Mengen sind, sind Intervallschachtelungen Beispiele für Folgen von Mengen. Die folgende Tabelle listet einige Beispiele für Folgen auf:

Art der Folge	Explizites Bildungsgesetz	Die ersten Folgenglieder
Reelle Folge $(a_{n})_{n\in \mathbb {N} }$	$a_{n}=n^{2}$	$1,\,4,\,9,\,16,\ldots$
Komplexe Folge $(c_{n})_{n\in \mathbb {N} }$	$c_{n}=i^{n}$	$i,\,-1,\,-i,\,1,\,i,\,\ldots$
Folge von Mengen $(M_{n})_{n\in \mathbb {N} }$	$M_{n}=\{k\in \mathbb {N} \,|\,k\leq n\}$	$\{1\},\,\{1,\,2\},\,\{1,\,2,\,3\},\,\{1,\,2,\,3,\,4\},\,\ldots$
Folge von Intervallen $(M_{n})_{n\in \mathbb {N} }$	$M_{n}=\left[-{\tfrac {1}{n}},\,{\tfrac {1}{n}}\right]$	$\left[-1,\,1\right],\,\left[-{\tfrac {1}{2}},\,{\tfrac {1}{2}}\right],\,\left[-{\tfrac {1}{3}},\,{\tfrac {1}{3}}\right],\,\left[-{\tfrac {1}{4}},\,{\tfrac {1}{4}}\right],\,\ldots$
Folge von Funktionen $(f_{n})_{n\in \mathbb {N} }$	$f_{n}:\mathbb {R} \rightarrow \mathbb {R} :x\mapsto {\tfrac {x^{2}}{n}}$	$f_{1}(x)=x^{2},\,f_{2}(x)={\tfrac {x^{2}}{2}},\,f_{3}(x)={\tfrac {x^{2}}{3}},\,f_{4}(x)={\tfrac {x^{2}}{4}},\ldots$

Das explizite Bildungsgesetz ist dabei diejenige Formel, mit der man ein Folgenglied in Abhängigkeit vom Index ausdrücken kann. Im nächsten Kapitel werden wir genauer auf die verschiedenen Bildungsgesetze für Folgen eingehen.